Peter K. Dunn · Gordon K. Smyth - Generalized Linear Models With

Springer Texts in Statistics

PeterK.Dunn· GordonK.Smyth

Generalized

Linear Models

With Examples

in R

Springer Texts in Statistics

Series Editors

R. DeVeaux

S.E. Fienberg

I. Olkin

More information about this series at http://www.springer.com/series/417

Peter K. Dunn • Gordon K. Smyth

Generalized Linear Models

With Examples in R

123

Peter K. Dunn

Faculty of Science, Health, Education

and Engineering

School of Health of Sport Science

University of the Sunshine Coast

QLD, Australia

Gordon K. Smyth

Bioinformatics Division

Walter and Eliza Hall Institute

of Medical Research

Parkville, VIC, Australia

ISSN 1431-875X ISSN 2197-4136 (electronic)

Springer Texts in Statistics

ISBN 978-1-4419-0117-0 ISBN 978-1-4419-0118-7 (eBook)

https://doi.org/10.1007/978-1-4419-0118-7

Library of Congress Control Number: 2018954737

This work is subject to copyright. All rights are reserved by the Publisher, whether the whole or part of

the material is concerned, speciﬁcally the rights of translation, reprinting, reuse of illustrations, recitation,

broadcasting, reproduction on microﬁlms or in any other physical way, and transmission or information

storage and retrieval, electronic adaptation, computer software, or by similar or dissimilar methodology

now known or hereafter developed.

The use of general descriptive names, registered names, trademarks, service marks, etc. in this publication

does not imply, even in the absence of a speciﬁc statement, that such names are exempt from the relevant

protective laws and regulations and therefore free for general use.

The publisher, the authors, and the editors are safe to assume that the advice and information in this book

are believed to be true and accurate at the date of publication. Neither the publisher nor the authors or

the editors give a warranty, express or implied, with respect to the material contained herein or for any

errors or omissions that may have been made. The publisher remains neutral with regard to jurisdictional

claims in published maps and institutional afﬁliations.

This Springer imprint is published by the registered company Springer Science+Business Media, LLC

part of Springer Nature.

The registered company address is: 233 Spring Street, New York, NY 10013, U.S.A.

To my wife Alison; our children Jessica,

Emily, Jemima, Samuel, Josiah and

Elijah; and my parents: Thank you for

your love and support and for giving so

much so I could get this far. PKD

To those who taught me about glms 40

years ago and to all the students who, in

the years since, have patiently listened to

me on the subject, given feedback and

generally made it rewarding to be a

teacher. GKS

Preface

A sophisticated analysis is wasted if the results cannot be

communicated eﬀectively to the client.

Reese [4, p. 201]

Our purpose in writing this book is to combine a good applied introduction to

generalized linear models (glms) with a thorough explanation of the theory

that is understandable from an elementary point of view.

We assume students to have basic knowledge of statistics and calculus. A

working familiarity with probability, probability distributions and hypothe-

sis testing is assumed, but a self-contained introduction to all other topics is

given in the book including linear regression. The early chapters of the book

give an introduction to linear regression and analysis of variance suitable

for a second course in statistics. Students with more advanced backgrounds,

including matrix algebra, will beneﬁt from optional sections that give a de-

tailed introduction to the theory and algorithms. The book can therefore be

read at multiple levels. It can be read by students with only a ﬁrst course in

statistics, but at the same time, it contains advanced material suitable for

graduate students and professionals.

The book should be appropriate for graduate students in statistics at either

the masters or PhD levels. It should be also be appropriate for advanced

undergraduate students taking majors in statistics in Britain or Australia.

Students in psychology, biometrics and related disciplines will also beneﬁt.

In general, it is appropriate for anyone wanting a practical working knowledge

of glms with a sound theoretical background.

r is a powerful and freely available environment for statistical computing

and graphics that has become widely adopted around the world. This book

includes a self-contained introduction to R (Appendix A), and use of r is

integrated into the text throughout the book. This includes comprehensive

r code examples and complete code for most data analyses and case studies.

Detailed use of relevant r functions is described in each chapter.

A practical working knowledge of good applied statistical practice is de-

veloped through the use of real data sets and numerous case studies. This

book makes almost exclusive use of real data. These data sets are collected in

the r package GLMsData [1] (see Appendix A for instructions for obtaining

vii

viii Preface

this r package), which has been prepared especially for use with this book

and which contains 97 data sets. Each example in the text is cross-referenced

with the relevant data set so that readers can load the relevant data to follow

the analysis in their own r session. Complete reproducible r code is provided

with the text for most examples.

The development of the theoretical background sometimes requires more

advanced mathematical techniques, including the use of matrix algebra. How-

ever, knowledge of these techniques is not required to read this book. We have

ensured that readers without this knowledge can still follow the theoretical

development, by ﬂagging the corresponding sections with a star * in the*

margin. Readers unfamiliar with these techniques may skip these sections

and problems without loss of continuity. However, those with the necessary

knowledge can gain more insight by reading the optional starred sections.

A set of problems is given at the end of each chapter and at the end of the

book. The balance between theory and practice is evident in the list of prob-

lems, which vary in diﬃculty and purpose. These problems cover many areas

of application and test understanding, theory, application, interpretation and

the ability to read publications that use glms.

This book begins with an introduction to multiple linear regression. In

abookaboutglms, at least three reasons exist for beginning with a short

discussion of multiple linear regression:

• Linear regression is familiar. Starting with regression consolidates this

material and establishes common notation, terminology and knowledge

for all readers. Notation and new terms are best introduced in a familiar

context.

• Linear regression is foundational. Many concepts and ideas from linear

regression are used as approximations in glms. A ﬁrm foundation in

linear regression ensures a better understanding of glms.

• Linear regression is motivational. Glmsoftenimprove linear regression.

Studying linear regression reveals its weaknesses and shows how glms

can often overcome most of these, motivating the need for glms.

Connections between linear regression and glms are emphasized throughout

this book.

This book contains a number of important but advanced topics and tools

that have not typically been included in introductions to glms before. These

include Tweedie family distributions with power variance functions, saddle-

point approximations, likelihood score tests, modiﬁed proﬁle likelihood and

randomized quantile residuals, as well as regression splines and orthogonal

polynomials. Particular features are the use of saddlepoint approximations

to clarify the asymptotical distribution of residual deviances from glmsand

an explanation of the relationship between score tests and Pearson statis-

tics. Practical and speciﬁc guidelines are developed for the use of asymptotic

approximations.

Preface ix

Throughout this book, r functions are shown in typewriter font fol-

lowed by parentheses; for example, glm(). Operators, data frames and vari-

ables in r are shown in typewriter font; for example, Smoke. r packages

are shown in bold and sans serif font; for example, GLMsData.

We thank those who have contributed to the writing of this book and

especially students who have contributed to earlier versions of this text. We

particularly thank Janette Benson, Alison Howes and Martine Maron for the

permission to use data.

This book was prepared using L

Xandr version 3.4.3 [3], integrated

using Sweave [2].

Sippy Downs, QLD, Australia Peter K. Dunn

Parkville, VIC, Australia Gordon K. Smyth

December 2017

References

[1] Dunn, P.K., Smyth, G.K.: GLMsData: Generalized linear model data sets

(2017). URL https://CRAN.R-project.org/package=GLMsData. R pack-

age version 1.0.0

[2] Leisch, F.: Dynamic generation of statistical reports using literate data

analysis. In: W. Härdle, B. Rönz (eds.) Compstat 2002—Proceedings

in Computational Statistics, pp. 575–580. Physika Verlag, Heidelberg,

Germany (2002)

[3] R Development Core Team: R: A Language and Environment for Statisti-

cal Computing. R Foundation for Statistical Computing, Vienna, Austria

(2017). URL https://www.R-project.org

[4] Reese, R.A.: Data analysis: The need for models? The Statistician 35(2),

199–206 (1986). Special Issue: Statistical Modelling

Contents

1 Statistical Models ......................................... 1

1.1 Introduction and Overview .............................. 1

1.2 Conventions for Describing Data ......................... 1

1.3 Plotting Data ......................................... 5

1.4 Coding for Factors ..................................... 10

1.5 Statistical Models Describe Both Random and Systematic

Features of Data ....................................... 11

1.6 Regression Models ..................................... 12

1.7 Interpreting Regression Models .......................... 16

1.8 All Models Are Wrong, but Some Are Useful .............. 17

1.9 The Purpose of a Statistical Model Aﬀects How It Is

Developed ............................................ 18

1.10 Accuracy vs Parsimony ................................. 19

1.11 Experiments vs Observational Studies: Causality

vs Association ......................................... 21

1.12 Data Collection and Generalizability ..................... 22

1.13 Using R for Statistical Modelling ........................ 23

1.14 Summary ............................................. 24

Problems ................................................... 25

References .................................................. 29

2 Linear Regression Models ................................. 31

2.1 Introduction and Overview .............................. 31

2.2 Linear Regression Models Deﬁned ........................ 31

2.3 Simple Linear Regression ............................... 35

2.3.1 Least-Squares Estimation ........................ 35

2.3.2 Coeﬃcient Estimates ............................ 36

2.3.3 Estimating the Variance σ

...................... 38

2.3.4 Standard Errors of the Coeﬃcients ................ 39

2.3.5 Standard Errors of Fitted Values ................. 39

xii Contents

2.4 Estimation for Multiple Regression ....................... 40

2.4.1 Coeﬃcient Estimates ............................ 40

2.4.2 Estimating the Variance σ

...................... 42

2.4.3 Standard Errors ................................ 42

* 2.5 Matrix Formulation of Linear Regression Models ........... 43

* 2.5.1 Matrix Notation ................................ 43

* 2.5.2 Coeﬃcient Estimates ............................ 44

* 2.5.3 Estimating the Variance σ

...................... 46

* 2.5.4 Estimating the Variance of

β ..................... 47

* 2.5.5 Estimating the Variance of Fitted Values .......... 47

2.6 Fitting Linear Regression Models Using R ................ 48

2.7 Interpreting the Regression Coeﬃcients ................... 52

2.8 Inference for Linear Regression Models: t-Tests ............ 53

2.8.1 Normal Linear Regression Models ................. 53

2.8.2 The Distribution of

........................... 53

2.8.3 Hypothesis Tests for β

.......................... 54

2.8.4 Conﬁdence Intervals for β

....................... 55

2.8.5 Conﬁdence Intervals for μ ........................ 56

2.9 Analysis of Variance for Regression Models ................ 58

2.10 Comparing Nested Models .............................. 61

2.10.1 Analysis of Variance to Compare Two Nested

Models ........................................ 61

2.10.2 Sequential Analysis of Variance ................... 63

2.10.3 Parallel and Independent Regressions .............. 66

2.10.4 The Marginality Principle ........................ 70

2.11 Choosing Between Non-nested Models: AIC and BIC ....... 70

2.12 Tools to Assist in Model Selection........................ 72

2.12.1 Adding and Dropping Variables................... 72

2.12.2 Automated Methods for Model Selection ........... 73

2.12.3 Objections to Using Stepwise Procedures .......... 76

2.13 Case Study ........................................... 76

2.14 Using R for Fitting Linear Regression Models ............. 79

2.15 Summary ............................................. 82

Problems ................................................... 83

References .................................................. 90

3 Linear Regression Models: Diagnostics

and Model-Building ....................................... 93

3.1 Introduction and Overview .............................. 93

3.2 Assumptions from a Practical Point of View ............... 94

3.2.1 Types of Assumptions ........................... 94

3.2.2 The Linear Predictor ............................ 94

3.2.3 Constant Variance .............................. 94

3.2.4 Independence .................................. 95

3.2.5 Normality ..................................... 96

Contents xiii

3.2.6 Measurement Scales ............................. 96

3.2.7 Approximations and Consequences ................ 96

3.3 Residuals for Normal Linear Regression Models ............ 97

3.4 The Leverages for Linear Regression Models ............... 98

3.4.1 Leverage and Extreme Covariate Values ........... 98

* 3.4.2 The Leverages Using Matrix Algebra .............. 100

3.5 Residual Plots ......................................... 101

3.5.1 Plot Residuals Against x

: Linearity .............. 101

3.5.2 Partial Residual Plots ........................... 102

3.5.3 Plot Residuals Against ˆμ: Constant Variance ....... 104

3.5.4 Q–Q Plots and Normality ........................ 105

3.5.5 Lag Plots and Dependence over Time ............. 106

3.6 Outliers and Inﬂuential Observations ..................... 108

3.6.1 Introduction ................................... 108

3.6.2 Outliers and Studentized Residuals ............... 109

3.6.3 Inﬂuential Observations ......................... 110

3.7 Terminology for Residuals .............................. 115

3.8 Remedies: Fixing Identiﬁed Problems ..................... 115

3.9 Transforming the Response ............................. 116

3.9.1 Symmetry, Constraints and the Ladder of Powers ... 116

3.9.2 Variance-Stabilizing Transformations .............. 117

3.9.3 Box–Cox Transformations........................ 120

3.10 Simple Transformations of Covariates ..................... 121

3.11 Polynomial Trends ..................................... 127

3.12 Regression Splines ..................................... 131

3.13 Fixing Identiﬁed Outliers ............................... 134

3.14 Collinearity ........................................... 135

3.15 Case Studies .......................................... 138

3.15.1 Case Study 1 ................................... 138

3.15.2 Case Study 2 ................................... 141

3.16 Using R for Diagnostic Analysis of Linear Regression

Models ............................................... 146

3.17 Summary ............................................. 147

Problems ................................................... 149

References .................................................. 162

4 Beyond Linear Regression: The Method of Maximum

Likelihood ................................................ 165

4.1 Introduction and Overview .............................. 165

4.2 The Need for Non-normal Regression Models .............. 165

4.2.1 When Linear Models Are a Poor Choice ........... 165

4.2.2 Binary Outcomes and Binomial Counts ............ 166

4.2.3 Unrestricted Counts: Poisson or Negative Binomial . . 168

4.2.4 Continuous Positive Observations ................. 169

4.3 Generalizing the Normal Linear Model ................... 171

xiv Contents

4.4 The Idea of Likelihood Estimation ....................... 172

4.5 Maximum Likelihood for Estimating One Parameter ....... 176

4.5.1 Score Equations ................................ 176

4.5.2 Information: Observed and Expected .............. 177

4.5.3 Standard Errors of Parameters ................... 179

4.6 Maximum Likelihood for More Than One Parameter ....... 180

4.6.1 Score Equations ................................ 180

4.6.2 Information: Observed and Expected .............. 182

4.6.3 Standard Errors of Parameters ................... 183

* 4.7 Maximum Likelihood Using Matrix Algebra ............... 183

* 4.7.1 Notation ....................................... 183

* 4.7.2 Score Equations ................................ 183

* 4.7.3 Information: Observed and Expected .............. 184

* 4.7.4 Standard Errors of Parameters ................... 186

* 4.8 Fisher Scoring for Computing MLEs ..................... 186

4.9 Properties of MLEs .................................... 189

4.9.1 Introduction ................................... 189

4.9.2 Properties of MLEs for One Parameter ............ 189

* 4.9.3 Properties of MLEs for Many Parameters .......... 190

4.10 Hypothesis Testing: Large Sample Asymptotic Results ...... 191

4.10.1 Introduction ................................... 191

* 4.10.2 Global Tests ................................... 194

* 4.10.3 Tests About Subsets of Parameters ............... 196

4.10.4 Tests About One Parameter in a Set of Parameters . 197

4.10.5 Comparing the Three Methods ................... 199

4.11 Conﬁdence Intervals .................................... 200

* 4.11.1 Conﬁdence Regions for More Than One Parameter . . 200

4.11.2 Conﬁdence Intervals for Single Parameters ......... 200

4.12 Comparing Non-nested Models: The AIC and BIC ......... 202

4.13 Summary ............................................. 204

* 4.14 Appendix: R Code to Fit Models to the Quilpie Rainfall

Data ................................................. 204

Problems ................................................... 206

References .................................................. 209

5 Generalized Linear Models: Structure ..................... 211

5.1 Introduction and Overview .............................. 211

5.2 The Two Components of Generalized Linear Models ........ 211

5.3 The Random Component: Exponential Dispersion Models . . . 212

5.3.1 Examples of EDMs ............................. 212

5.3.2 Deﬁnition of EDMs ............................. 212

5.3.3 Generating Functions ........................... 214

5.3.4 The Moment Generating and Cumulant Functions

for EDMs ...................................... 215

5.3.5 The Mean and Variance of an EDM ............... 216

Contents xv

5.3.6 The Variance Function .......................... 217

5.4 EDMs in Dispersion Model Form ........................ 218

5.4.1 The Unit Deviance and the Dispersion Model Form ... 218

5.4.2 The Saddlepoint Approximation .................. 223

5.4.3 The Distribution of the Unit Deviance ............. 224

5.4.4 Accuracy of the Saddlepoint Approximation ........ 225

5.4.5 Accuracy of the χ

Distribution for the Unit

Deviance ...................................... 226

5.5 The Systematic Component ............................. 229

5.5.1 Link Function .................................. 229

5.5.2 Oﬀsets ........................................ 229

5.6 Generalized Linear Models Deﬁned ....................... 230

5.7 The Total Deviance .................................... 231

5.8 Regression Transformations Approximate GLMs ........... 232

5.9 Summary ............................................. 234

Problems ................................................... 235

References .................................................. 240

6 Generalized Linear Models: Estimation ................... 243

6.1 Introduction and Overview .............................. 243

6.2 Likelihood Calculations for β ............................ 243

6.2.1 Diﬀerentiating the Probability Function ........... 243

6.2.2 Score Equations and Information for β ............ 244

6.3 Computing Estimates of β .............................. 245

6.4 The Residual Deviance ................................. 248

6.5 Standard Errors for

β .................................. 250

* 6.6 Estimation of β: Matrix Formulation ..................... 250

6.7 Estimation of GLMs Is Locally Like Linear Regression ...... 252

6.8 Estimating φ .......................................... 252

6.8.1 Introduction ................................... 252

6.8.2 The Maximum Likelihood Estimator of φ .......... 253

6.8.3 Modiﬁed Proﬁle Log-Likelihood Estimator of φ ..... 253

6.8.4 Mean Deviance Estimator of φ ................... 254

6.8.5 Pearson Estimator of φ .......................... 255

6.8.6 Which Estimator of φ Is Best? ................... 255

6.9 Using R to Fit GLMs .................................. 257

6.10 Summary ............................................. 259

Problems ................................................... 261

References .................................................. 262

7 Generalized Linear Models: Inference ..................... 265

7.1 Introduction and Overview .............................. 265

7.2 Inference for Coeﬃcients When φ Is Known ............... 265

7.2.1 Wald Tests for Single Regression Coeﬃcients ....... 265

7.2.2 Conﬁdence Intervals for Individual Coeﬃcients ..... 266

xvi Contents

7.2.3 Conﬁdence Intervals for μ ........................ 267

7.2.4 Likelihood Ratio Tests to Compare Nested Models:

Tests ....................................... 269

7.2.5 Analysis of Deviance Tables to Compare Nested

Models ........................................ 270

7.2.6 Score Tests .................................... 271

* 7.2.7 Score Tests Using Matrices ....................... 272

7.3 Large Sample Asymptotics .............................. 273

7.4 Goodness-of-Fit Tests with φ Known ..................... 274

7.4.1 The Idea of Goodness-of-Fit ...................... 274

7.4.2 Deviance Goodness-of-Fit Test ................... 275

7.4.3 Pearson Goodness-of-Fit Test .................... 275

7.5 Small Dispersion Asymptotics ........................... 276

7.6 Inference for Coeﬃcients When φ Is Unknown ............. 278

7.6.1 Wald Tests for Single Regression Coeﬃcients ....... 278

7.6.2 Conﬁdence Intervals for Individual Coeﬃcients ..... 280

* 7.6.3 Conﬁdence Intervals for μ ........................ 281

7.6.4 Likelihood Ratio Tests to Compare Nested Models:

F -Tests ........................................ 282

7.6.5 Analysis of Deviance Tables to Compare Nested

Models ........................................ 284

7.6.6 Score Tests .................................... 286

7.7 Comparing Wald, Score and Likelihood Ratio Tests ........ 287

7.8 Choosing Between Non-nested GLMs: AIC and BIC ........ 288

7.9 Automated Methods for Model Selection .................. 289

7.10 Using R to Perform Tests ............................... 290

7.11 Summary ............................................. 292

Problems ................................................... 293

References .................................................. 296

8 Generalized Linear Models: Diagnostics ................... 297

8.1 Introduction and Overview .............................. 297

8.2 Assumptions of GLMs .................................. 297

8.3 Residuals for GLMs .................................... 298

8.3.1 Response Residuals Are Insuﬃcient for GLMs ...... 298

8.3.2 Pearson Residuals .............................. 299

8.3.3 Deviance Residuals ............................. 300

8.3.4 Quantile Residuals .............................. 300

8.4 The Leverages in GLMs ................................ 304

8.4.1 Working Leverages .............................. 304

* 8.4.2 The Hat Matrix ................................ 304

8.5 Leverage Standardized Residuals for GLMs ............... 305

8.6 When to Use Which Type of Residual .................... 306

8.7 Checking the Model Assumptions ........................ 306

8.7.1 Introduction ................................... 306

Contents xvii

8.7.2 Independence: Plot Residuals Against Lagged

Residuals ...................................... 307

8.7.3 Plots to Check the Systematic Component ......... 307

8.7.4 Plots to Check the Random Component ........... 311

8.8 Outliers and Inﬂuential Observations ..................... 312

8.8.1 Introduction ................................... 312

8.8.2 Outliers and Studentized Residuals ............... 312

8.8.3 Inﬂuential Observations ......................... 313

8.9 Remedies: Fixing Identiﬁed Problems ..................... 315

8.10 Quasi-Likelihood and Extended Quasi-Likelihood .......... 318

8.11 Collinearity ........................................... 321

8.12 Case Study ........................................... 322

8.13 Using R for Diagnostic Analysis of GLMs ................. 325

8.14 Summary ............................................. 326

Problems ................................................... 327

References .................................................. 330

9 Models for Proportions: Binomial GLMs .................. 333

9.1 Introduction and Overview .............................. 333

9.2 Modelling Proportions .................................. 333

9.3 Link Functions ........................................ 336

9.4 Tolerance Distributions and the Probit Link ............... 338

9.5 Odds, Odds Ratios and the Logit Link .................... 340

9.6 Median Eﬀective Dose, ED50 ............................ 343

9.7 The Complementary Log-Log Link in Assay Analysis ....... 344

9.8 Overdispersion ........................................ 347

9.9 When Wald Tests Fail .................................. 351

9.10 No Goodness-of-Fit for Binary Responses ................. 354

9.11 Case Study ........................................... 354

9.12 Using R to Fit GLMs to Proportion Data ................. 360

9.13 Summary ............................................. 360

Problems ................................................... 361

References .................................................. 367

10 Models for Counts: Poisson and Negative Binomial GLMs 371

10.1 Introduction and Overview .............................. 371

10.2 Summary of Poisson GLMs ............................. 371

10.3 Modelling Rates ....................................... 373

10.4 Contingency Tables: Log-Linear Models ................... 378

10.4.1 Introduction ................................... 378

10.4.2 Two Dimensional Tables: Systematic Component ... 378

10.4.3 Two-Dimensional Tables: Random Components ..... 380

10.4.4 Three-Dimensional Tables ....................... 385

10.4.5 Simpson’s Paradox .............................. 389

10.4.6 Equivalence of Binomial and Poisson GLMs ........ 392

xviii Contents

10.4.7 Higher-Order Tables ............................ 393

10.4.8 Structural Zeros in Contingency Tables ............ 395

10.5 Overdispersion ........................................ 397

10.5.1 Overdispersion for Poisson GLMs ................. 397

10.5.2 Negative Binomial GLMs ........................ 399

10.5.3 Quasi-Poisson Models ........................... 402

10.6 Case Study ........................................... 404

10.7 Using R to Fit GLMs to Count Data ..................... 411

10.8 Summary ............................................. 411

Problems ................................................... 412

References .................................................. 422

11 Positive Continuous Data: Gamma and Inverse Gaussian

GLMs ..................................................... 425

11.1 Introduction and Overview .............................. 425

11.2 Modelling Positive Continuous Data ...................... 425

11.3 The Gamma Distribution ............................... 427

11.4 The Inverse Gaussian Distribution ....................... 431

11.5 Link Functions ........................................ 433

11.6 Estimating the Dispersion Parameter ..................... 436

11.6.1 Estimating φ for the Gamma Distribution ......... 436

11.6.2 Estimating φ for the Inverse Gaussian Distribution . . 439

11.7 Case Studies .......................................... 440

11.7.1 Case Study 1 ................................... 440

11.7.2 Case Study 2 ................................... 442

11.8 Using R to Fit Gamma and Inverse Gaussian GLMS ....... 445

11.9 Summary ............................................. 445

Problems ................................................... 446

References .................................................. 454

12 Tweedie GLMs ............................................ 457

12.1 Introduction and Overview .............................. 457

12.2 The Tweedie EDMs .................................... 457

12.2.1 Introducing Tweedie Distributions ................ 457

12.2.2 The Structure of Tweedie EDMs .................. 460

12.2.3 Tweedie EDMs for Positive Continuous Data ....... 461

12.2.4 Tweedie EDMs for Positive Continuous Data with

Exact Zeros .................................... 463

12.3 Tweedie GLMs ........................................ 464

12.3.1 Introduction ................................... 464

12.3.2 Estimation of the Index Parameter ξ .............. 465

12.3.3 Fitting Tweedie GLMs .......................... 469

12.4 Case Studies .......................................... 473

12.4.1 Case Study 1 ................................... 473

12.4.2 Case Study 2 ................................... 475

Contents xix

12.5 Using R to Fit Tweedie GLMs ........................... 478

12.6 Summary ............................................. 479

Problems ................................................... 480

References .................................................. 488

13 Extra Problems ........................................... 491

13.1 Introduction and Overview .............................. 491

Problems ................................................... 491

References .................................................. 500

Using R for Data Analysis .................................... 503

A.1 Introduction and Overview .............................. 503

A.2 Preparing to Use R .................................... 503

A.2.1 Introduction to R ............................... 503

A.2.2 Important R Websites ........................... 504

A.2.3 Obtaining and Installing R ....................... 504

A.2.4 Downloading and Installing R Packages ............ 504

A.2.5 Using R Packages ............................... 505

A.2.6 The R Packages Used in This Book ............... 506

A.3 Introduction to Using R ................................ 506

A.3.1 Basic Use of R as an Advanced Calculator ......... 506

A.3.2 Quitting R ..................................... 508

A.3.3 Obtaining Help in R ............................ 508

A.3.4 Variable Names in R ............................ 508

A.3.5 Working with Vectors in R ....................... 509

A.3.6 Loading Data into R ............................ 511

A.3.7 Working with Data Frames in R .................. 513

A.3.8 Using Functions in R ............................ 514

A.3.9 Basic Statistical Functions in R ................... 515

A.3.10 Basic Plotting in R ............................. 516

A.3.11 Writing Functions in R .......................... 518

* A.3.12 Matrix Arithmetic in R .......................... 520

References .................................................. 523

The GLMsData package ....................................... 525

References .................................................. 527

Selected Solutions ............................................ 529

Solutions from Chap. 1 ....................................... 529

Solutions from Chap. 2 ....................................... 530

Solutions from Chap. 3 ....................................... 532

Solutions from Chap. 4 ....................................... 534

Solutions from Chap. 5 ....................................... 536

Solutions from Chap. 6 ....................................... 537

Solutions from Chap. 7 ....................................... 537

Solutions from Chap. 8 ....................................... 539

xx Contents

Solutions from Chap. 9 ....................................... 539

Solutions from Chap. 10 ...................................... 541

Solutions from Chap. 11 ...................................... 544

Solutions from Chap. 12 ...................................... 547

Solutions from Chap. 13 ...................................... 548

References .................................................. 550

Index: Data sets .............................................. 551

Index: R commands .......................................... 553

Index: General topics ......................................... 557

Chapter 1

Statistical Models

...all models are approximations. Essentially, all models

are wrong, but some are useful. However, the approximate

nature of the model must always be borne in mind.

Box and Draper [2, p. 424]

1.1 Introduction and Overview

This chapter introduces the concept of a statistical model. One particular

type of statistical model—the generalized linear model—is the focus of this

book, and so we begin with an introduction to statistical models in gen-

eral. This allows us to introduce the necessary language, notation, and other

important issues. We ﬁrst discuss conventions for describing data mathemati-

cally (Sect. 1.2). We then highlight the importance of plotting data (Sect. 1.3),

and explain how to numerically code non-numerical variables (Sect. 1.4)so

that they can be used in mathematical models. We then introduce the two

components of a statistical model used for understanding data (Sect. 1.5):

the systematic and random components. The class of regression models is

then introduced (Sect. 1.6), which includes all models in this book. Model

interpretation is then considered (Sect. 1.7), followed by comparing physical

models and statistical models (Sect. 1.8) to highlight the similarities and dif-

ferences. The purpose of a statistical model is then given (Sect. 1.9), followed

by a description of the two criteria for evaluating statistical models: accuracy

and parsimony (Sect. 1.10). The importance of understanding the limitations

of statistical models is then addressed (Sect. 1.11), including the diﬀerences

between observational and experimental data. The generalizability of models

is then discussed (Sect. 1.12). Finally, we make some introductory comments

about using r for statistical modelling (Sect. 1.13).

1.2 Conventions for Describing Data

The concepts in this chapter are best introduced using an example.

Example 1.1. A study of 654 youths in East Boston [10, 18, 20] explored the

relationships between lung capacity (measured by forced expiratory volume,

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_1

21StatisticalModels

or fev, in litres) and smoking status, age, height and gender (Table 1.1). The

data are available in r as the data frame lungcap (short for ‘lung capacity’),

part of the GLMsData package [4]. For information about this package, see

Appendix B; for more information about r, see Appendix A. Assuming the

GLMsData package is installed in r (see Sect. A.2.4), load the GLMsData

package and the lungcap data frame as follows:

> library(GLMsData) # Load the GLMsData package

> data(lungcap) # Make the data set lungcap available for use

> head(lungcap) # Show the first few lines of data

Age FEV Ht Gender Smoke

1 3 1.072 46 F 0

2 4 0.839 48 F 0

3 4 1.102 48 F 0

4 4 1.389 48 F 0

5 4 1.577 49 F 0

6 4 1.418 49 F 0

(The # character and all subsequent text is ignored by r.) The data frame

lungcap consist of ﬁve variables: Age, FEV, Ht, Gender and Smoke. Some

of these variables are numerical variables (such as Age), and some are non-

numerical variables (such as Gender). Any one of these can be accessed indi-

vidually using $ as follows:

> head(lungcap$Age) # Show first six values of Age

[1]344444

> tail(lungcap$Gender) # Show last six values of Gender

[1]MMMMMM

Levels: F M

Tabl e 1. 1 The forced expiratory volume (fev) of youths, sampled from East Boston

during the middle to late 1970s. fev is in L; age is in completed years; height is in inches.

The complete data set consists of 654 observations in total (Example 1.1)

Non-smokers Smokers

Females Males Females Males

fev Age Height fev Age Height fev Age Height fev Age Height

1.072 3 46.0 1.404 3 51.5 2.975 10 63.0 1.953 9 58.0

0.839 4 48.0 0.796 4 47.0 3.038 10 65.0 3.498 10 68.0

1.102 4 48.0 1.004 4 48.0 2.387 10 66.0 1.694 11 60.0

1.389 4 48.0 1.789 4 52.0 3.413 10 66.0 3.339 11 68.5

1.577 4 49.0 1.472 5 50.0 3.120 11 61.0 4.637 11 72.0

1.418 4 49.0 2.115 5 50.0 3.169 11 62.5 2.304 12 66.5

1.569 4 50.0 1.359 5 50.5 3.102 11 64.0 3.343 12 68.0

1.196 5 46.5 1.776 5 51.0 3.069 11 65.0 3.751 12 72.0

1.400 5 49.0 1.452 5 51.0 2.953 11 67.0 4.756 13 68.0

1.282 5 49.0 1.930 5 51.0 3.104 11 67.5 4.789 13 69.0

1.2 Conventions for Describing Data 3

The length of any one variable is found using length():

> length(lungcap$Age)

[1] 654

The dimension of the data set is:

> dim(lungcap)

[1] 654 5

That is, there are 654 cases and 5 variables. 

For these data, the sample size, usually denoted as n,isn = 654. Each

youth’s information is recorded in one row of the r data frame. fev is called

the response variable (or the dependent variable) since fev is assumed to

change in response to (or depends on) the values of the other variables. The

response variable is usually denoted by y. In Example 1.1, y refers to ‘fev

(in litres)’. When necessary, y

refers to the ith value of the response. For

example, y

=1.072 in Table 1.1. Occasionally it is convenient to refer to all

the observations y

together instead of one at a time.

The other variables—age, height, gender and smoking status—can be

called candidate variables, carriers, exogenous variables, independent vari-

ables, input variables, predictors, or regressors. We call these variables ex-

planatory variables in this book. Explanatory variables are traditionally de-

noted by x. In Example 1.1,letx

refer to age (in completed years), and x

refer to height (in inches). When necessary, the value of, say, x

for Observa-

tion i is denoted x

; for example, x

2,1

= 46.

Distinguishing between quantitative and qualitative explanatory variables

is essential. Explanatory variables that are qualitative, like gender, are called

factors. Gender is a factor with two levels: F (female) and M (male). Explana-

tory variables that are quantitative, like height and age, are called covariates.

Often, the key question of interest in an analysis concerns the relationship

between the response variable and one or more explanatory variables, though

other explanatory variables are present and may also inﬂuence the response.

Adjusting for the eﬀects of other correlated variables is often necessary, so as

to understand the eﬀect of the variable of key interest. These other variables

are sometimes called extraneous variables. For example, we may be inter-

ested in the relationship between fev (as the response variable) and smok-

ing status (as the explanatory variable), but acknowledge that age, height

and gender may also inﬂuence fev. Age, height and gender are extraneous

variables.

41StatisticalModels

Example 1.2. Viewing the structure of a data frame can be informative:

> str(lungcap) # Show the *structure* of the data frame

'data.frame': 654 obs. of 5 variables:

$Age :int 3444444555...

$ FEV : num 1.072 0.839 1.102 1.389 1.577 ...

$ Ht : num 46 48 48 48 49 49 50 46.5 49 49 ...

$ Gender: Factor w/ 2 levels "F","M": 1111111111...

$ Smoke : int 0000000000...

The size of the data frame is given, plus information about each variable: Age

and Smoke consists of integers, FEV and Ht are numerical, while Gender is a

factor with two levels. Each variable can be summarized numerically using

summary():

> summary(lungcap) # Summarize the data

Age FEV Ht Gender

Min. : 3.000 Min. :0.791 Min. :46.00 F:318

1st Qu.: 8.000 1st Qu.:1.981 1st Qu.:57.00 M:336

Median :10.000 Median :2.547 Median :61.50

Mean : 9.931 Mean :2.637 Mean :61.14

3rd Qu.:12.000 3rd Qu.:3.119 3rd Qu.:65.50

Max. :19.000 Max. :5.793 Max. :74.00

Smoke

Min. :0.00000

1st Qu.:0.00000

Median :0.00000

Mean :0.09939

3rd Qu.:0.00000

Max. :1.00000

Notice that quantitative variables are summarized diﬀerently to qualitative

variables. FEV, Age and Ht (all quantitative) are summarized with the mini-

mum and maximum values, the ﬁrst and third quartiles, and the mean and

median. Gender (qualitative) is summarised by giving the number of males

and females in the data. The variable Smoke is qualitative, and numbers are

used to designate the levels of the variable. In this case, r has no way of

determining if the variable is a factor or not, and assumes the variable is

quantitative by default since it consists of numbers. To explicitly tell r that

Smoke is qualitative, use factor():

> lungcap$Smoke <- factor(lungcap$Smoke,

levels=c(0, 1), # The values of Smoke

labels=c("Non-smoker","Smoker")) # The labels

> summary(lungcap$Smoke) # Now, summarize the redefined variable Smoke

Non-smoker Smoker

589 65

(The information about the data set, accessed using ?lungcap, explains

that 0 represents non-smokers and 1 represents smokers.) We notice that

non-smokers outnumber smokers. 

1.3 Plotting Data 5

1.3 Plotting Data

Understanding the lung capacity data is diﬃcult because there is so much

data. How can the impact of age, height, gender and smoking status on

fev be understood? Plots (Fig. 1.1) may reveal many, but probably not all,

important features of the data:

> plot( FEV ~ Age, data=lungcap,

xlab="Age (in years)", # The x-axis label

ylab="FEV (in L)", # The y-axis label

main="FEV vs age", # The main title

xlim=c(0, 20), # Explicitly set x-axis limits

ylim=c(0, 6), # Explicitly set y-axis limits

las=1) # Makes axis labels horizontal

This r code uses the plot() command to produce plots of the data. (For more

information on plotting in r, see Sect. A.3.10.) The formula FEV ~ Age is read

as ‘FEV is modelled by Age’. The input data=lungcap indicates that lungcap

is the data frame in which to ﬁnd the variables FEV and Age. Continue by

plotting FEV against the remaining variables:

> plot( FEV ~ Ht, data=lungcap, main="FEV vs height",

xlab="Height (in inches)", ylab="FEV (in L)",

las=1, ylim=c(0, 6) )

> plot( FEV ~ Gender, data=lungcap,

main="FEV vs gender", ylab="FEV (in L)",

las=1, ylim=c(0, 6))

> plot( FEV ~ Smoke, data=lungcap, main="FEV vs Smoking status",

ylab="FEV (in L)", xlab="Smoking status",

las=1, ylim=c(0, 6))

(Recall that Smoke was declared a factor in Example 1.2.) Notice that r

uses diﬀerent types of displays for plotting fev against covariates (top pan-

els) than against factors (bottom panels). Boxplots are used (by default)

for plotting fev against factors: the solid horizontal centre line in each box

represents the median (not the mean), and the limits of the central box rep-

resent the upper and lower quartiles of the data (approximately 75% of the

observations are less than the upper quartile, and approximately 25% of the

observations are less than the lower quartile). The lines from the central box

extend to the largest and smallest values, except for outliers which are in-

dicated by individual points (such as a large fev for a few smokers). In r,

outliers are deﬁned, by default, as observations more than 1.5 times the inter-

quartile range (the diﬀerence between the upper and lower quartiles) more

extreme than the upper or lower limits of the central box.

The plots (Fig. 1.1) show a moderate relationship (reasonably large vari-

ation) between fev and age, that is possibly linear (at least until about 15

years of age). However, a stronger relationship (less variation) is apparent

between fev and height, but this relationship does not appear to be linear.

61StatisticalModels

0 5 10 15 20

FEV vs age

Age (in years)

FEV (in L)

45 50 55 60 65 70 75

FEV vs height

Height (in inches)

FEV (in L)

FEV vs gender

Gender

FEV (in L)

Non−smoker Smoker

FEV vs Smoking status

Smoking status

FEV (in L)

Fig. 1.1 Forced expiratory volume (fev ) plotted against age (top left), height (top

right), gender (bottom left) and smoking status (bottom right) for the data in Table 1.1

(Sect. 1.3)

The variation in fev appears to increase for larger values of fev also. In gen-

eral, it also appears that males have a slightly larger fev, and show greater

variation in fev, than females. Smokers appear to have a larger fev than

non-smokers.

While many of these statements are expected, the ﬁnal statement is sur-

prising, and may suggest that more than one variable should be examined at

once. The plots in Fig. 1.1 only explore the relationships between fev and

each explanatory variable individually, so we continue by exploring relation-

ships involving more than two variables at a time.

One way to do this is to plot the data separately for smokers and non-

smokers (Fig. 1.2), using similar scales on the axes to enable comparisons:

> plot( FEV ~ Age,

data=subset(lungcap, Smoke=="Smoker"), # Only select smokers

main="FEV vs age\nfor smokers", # \n means `new line'

ylab="FEV (in L)", xlab="Age (in years)",

ylim=c(0, 6), xlim=c(0, 20), las=1)

1.3 Plotting Data 7

0 5 10 15 20

FEV vs age

for smokers

Age (in years)

FEV (in L)

0 5 10 15 20

FEV vs age

for non−smokers

Age (in years)

FEV (in L)

45 50 55 60 65 70 75

FEV vs height

for smokers

Height (in inches)

FEV (in L)

45 50 55 60 65 70 75

FEV vs height

for non−smokers

Height (in inches)

FEV (in L)

Fig. 1.2 Plots of the lung capacity data: the forced expiratory volume (fev) plotted

against age, for smokers (top left panel) and non-smokers (top right panel); and the

forced expiratory volume (fev ) plotted against height, for smokers (bottom left panel)

and non-smokers (bottom right panel) (Sect. 1.3)

> plot( FEV ~ Age,

data=subset(lungcap, Smoke=="Non-smoker"), # Only select non-smokers

main="FEV vs age\nfor non-smokers",

ylab="FEV (in L)", xlab="Age (in years)",

ylim=c(0, 6), xlim=c(0, 20), las=1)

> plot( FEV ~ Ht, data=subset(lungcap, Smoke=="Smoker"),

main="FEV vs height\nfor smokers",

ylab="FEV (in L)", xlab="Height (in inches)",

xlim=c(45, 75), ylim=c(0, 6), las=1)

> plot( FEV ~ Ht, data=subset(lungcap, Smoke=="Non-smoker"),

main="FEV vs height\nfor non-smokers",

ylab="FEV (in L)", xlab="Height (in inches)",

xlim=c(45, 75), ylim=c(0, 6), las=1)

Note that == is used to make logical comparisons. The plots show that smok-

ers tend to be older (and hence taller) than non-smokers and hence are likely

to have a larger fev.

81StatisticalModels

Another option is to distinguish between smokers and non-smokers when

plotting the FEV against Age. For these data, there are so many observa-

tions that distinguishing between smokers and non-smokers is diﬃcult, so we

ﬁrst adjust Age so that the values for smokers and non-smokers are slightly

separated:

> AgeAdjust <- lungcap$Age + ifelse(lungcap$Smoke=="Smoker", 0, 0.5)

The code ifelse( lungcap$Smoke=="Smoker", 0, 0.5) adds zero to the

value of Age for youth labelled with Smoker, and adds 0.5 to youth labelled

otherwise (that is, non-smokers). Then we plot fev against this variable:

(Fig. 1.3, top left panel):

> plot( FEV ~ AgeAdjust, data=lungcap,

pch = ifelse(Smoke=="Smoker", 3, 20),

xlab="Age (in years)", ylab="FEV (in L)", main="FEV vs age", las=1)

The input pch indicates the plotting character to use when plotting; then,

ifelse( Smoke=="Smoker", 3, 20) means to plot with plotting charac-

ter 3 (a ‘plus’ sign) if Smoke takes the value "Smoker", and otherwise to

plot with plotting character 20 (a ﬁlled circle). See ?points for an explana-

tion of the numerical codes used to deﬁne diﬀerent plotting symbols. Recall

that in Example 1.2, Smoke was declared as a factor with two levels that

were labelled Smoker and Non-smoker.Thelegend() command produces

the legend:

> legend("topleft", pch=c(20, 3), legend=c("Non-smokers","Smokers") )

The ﬁrst input speciﬁes the location (such as "center" or "bottomright").

The second input gives the plotting notation to be explained (such as the

points, using pch, or the line types, using lty). The legend input provides

the explanatory text. Use ?legend for more information.

A boxplot can also be used to show relationships (Fig. 1.3, top right panel):

> boxplot(lungcap$FEV ~ lungcap$Smoke + lungcap$Gender,

ylab="FEV (in L)", main="FEV, by gender\n and smoking status",

las=2, # Keeps labels perpendicular to the axes

names=c("F:\nNon", "F:\nSmoker", "M:\nNon", "M:\nSmoker"))

Another way to show the relationship between three variables is to use

an interaction plot, which shows the relationship between the levels of two

factors and (by default) the mean response of a quantitative variable. The

appropriate r function is interaction.plot() (Fig. 1.3, bottom panels):

> interaction.plot( lungcap$Smoke, lungcap$Gender, lungcap$FEV,

xlab="Smoking status", ylab="FEV (in L)",

main="Mean FEV, by gender\n and smoking status",

trace.label="Gender", las=1)

> interaction.plot( lungcap$Smoke, lungcap$Gender, lungcap$Age,

xlab="Smoking status", ylab="Age (in years)",

main="Mean age, by gender\n and smoking status",

trace.label="Gender", las=1)

1.3 Plotting Data 9

5101520

FEV vs age

Age (in years)

FEV (in L)

Non−smokers

Smokers

Non

Smoker

Non

Smoker

FEV, by gender

and smoking status

FEV (in L)

2.4

2.6

2.8

3.0

3.2

3.4

3.6

Mean FEV, by gender

and smoking status

Smoking status

FEV (in L)

Non−smoker Smoker

Gender

Mean age, by gender

and smoking status

Smoking status

Age (in years)

Non−smoker Smoker

Gender

Fig. 1.3 Plots of the lung capacity data: the forced expiratory volume (fev)plot-

ted against age, using diﬀerent plotting symbols for non-smokers and smokers (top left

panel); a boxplot of fev against gender and smoking status (top right panel); an inter-

action plot of the mean fev against smoking status according to gender (bottom left

panel); and an interaction plot of the mean age against smoking status according to

gender (bottom right panel) (Sect. 1.3)

This plot shows that, in general, smokers have a larger fev than non-

smokers, for both males and females. The plot also shows that the mean age

of smokers is higher for both males and females.

To make any further progress quantifying the relationship between the

variables, mathematics is necessary to create a statistical model.

10 1 Statistical Models

1.4 Coding for Factors

Factors represent categories (such as smokers or non-smokers, or males and

females), and so must be coded numerically to be used in mathematical mod-

els. This is achieved by using dummy variables.

The variable Gender in the lungcap data frame is loaded as a factor by

default, as the data are non-numerical:

> head(lungcap$Gender)

[1]FFFFFF

Levels: F M

To show the coding used by r for the variable Gender in the lungcap data

set, use contrasts():

> contrasts(lungcap$Gender)

(The function name is because, under certain conditions, the codings are

called contrasts.) The output shows the two levels of Gender on the left, and

the name of the dummy variable across the top. When the dummy variable M

is equal to one, the dummy variable refers males. Notice F is not listed across

the top of the output as a dummy variable, since it is the reference level.By

default in r, the reference level is the ﬁrst level alphabetically or numerically.

In other words, the dummy variable, say x

,is:



0ifGender is F (females)

1ifGender is M (males).

(1.1)

Since these numerical codes are arbitrarily assigned, other levels may be set

as the reference level in r using relevel():

> contrasts( relevel( lungcap$Gender, "M") ) # Now, M is the ref. level

As seen earlier in Example 1.2,ther function factor() is used to explicitly

declare a variable as a factor when necessary (for example, if the data use

numbers to designate the factor levels):

> lungcap$Smoke <- factor(lungcap$Smoke,

levels=c(0, 1),

labels=c("Non-smoker","Smoker"))

> contrasts(lungcap$Smoke)

Smoker

Non-smoker 0

Smoker 1

1.5 Statistical Models Describe Both Random and Systematic Features of Data 11

This command assigns the values of 0 and 1 to the labels Non-smoker and

Smoker respectively:



0ifSmoke is 0 (non-smoker)

1ifSmoke is 1 (smokers).

(1.2)

For a factor with k levels, k −1 dummy variables are needed. For example,

if smoking status had three levels (for example, ‘Never smoked’, ‘Former

smoker’, ‘Current smoker’), then two dummy variables are needed:



1 for former smokers

0 otherwise;



1 for current smokers

0 otherwise.

(1.3)

Then x

= x

= 0 uniquely refers to people who have never smoked.

The coding discussed here is called treatment coding. Many types of coding

exist to numerically code factors. Treatment coding is commonly used (and

is used in this book, and in r by default) since it usually leads to a direct

interpretation. Other codings are also possible, with diﬀerent interpretations

useful in diﬀerent contexts. In any analysis, the deﬁnition of the dummy

variables being used should be made clear.

1.5 Statistical Models Describe Both Random

and Systematic Features of Data

Consider again the lung capacity data from Example 1.1 (p. 1). At any given

combination of height, age, gender and smoking status, many diﬀerent values

of fev could be recorded, and so produce a distribution of recorded fev

values. A model for this distribution of values is called the random component

of the statistical model. At this given combination of height, age, gender

and smoking status, the distribution of fev values has a mean fev.The

mathematical relationship between the mean fev and given values of height,

age, gender and smoking status is called the systematic component of the

model. A statistical model consists of a random component and a systematic

component to explain these two features of real data. In this context, the role

of a statistical model is to mathematically represent both the systematic and

random components of data.

Many systematic components for the lung capacity data are possible. One

simple systematic component is

= β

+ β

(1.4)

for Observation i, where μ

is the expected value of y

,sothatμ

=E[y

]

for i =1, 2,...,n.Theβ

(for j =0, 1, 2, 3 and 4) are unknown regression

parameters. The explanatory variables are age x

, height x

, the dummy

12 1 Statistical Models

variable x

deﬁned in (1.1) for gender, and the dummy variable x

deﬁned

in (1.2) for smoking status. This is likely to be a poor systematic component,

as the plots (Fig. 1.1) show that the relationship between fev and height is

non-linear, for example. Other systematic components are also possible.

The randomness about this systematic component may take many forms.

For example, using var[y

]=σ

assumes that the variance of the responses

is constant about μ

, but makes no assumptions about the distribution

of the responses. A popular assumption is to assume the responses have a

normal distribution about the mean μ

with constant variance σ

, written

∼ N (μ

,σ

), where ‘∼’ means ‘is distributed as’. Both assumptions are

likely to be poor for the lung capacity data, as the plots (Fig. 1.1) show that

the variation in the observed fev increases for larger values of fev. Other

assumptions are also possible, such as assuming the responses come from

other probability distributions beside the normal distribution.

1.6 Regression Models

The systematic component (1.4) for the lung capacity data is one possible rep-

resentation for explaining how the mean fev changes as height, age, gender

and smoking status vary. Many other representation are also possible. Very

generally, a regression model assumes that the mean response μ

for Obser-

vation i depends on the p explanatory variables x

to x

via some general

function f through a number of regression parameters β

(for j =0, 1,...q).

Mathematically,

E[y

]=μ

= f(x

,...,x

; β

,β

,...,β

Commonly, the parameters β

are assumed to combine the eﬀects of the

explanatory variables linearly, so that the systematic component often takes

the more speciﬁc form

= f(β

+ β

+ ···+ β

). (1.5)

Regression models with this form (1.5)areregression models linear in the

parameters. All the models discussed in this book are regression models linear

in the parameters. The component β

+β

+···+β

is called the linear

predictor.

Two special types of regression models linear in the parameters are dis-

cussed in detail in this book:

• Linear regression models: The systematic component of a linear regression

model assumes the form

E[y

]=μ

= β

+ β

+ ···+ β

, (1.6)

1.6 Regression Models 13

while the randomness is assumed to have constant variance σ

about μ

Linear regression models are formally deﬁned and discussed in Chaps. 2

and 3.

• Generalized linear models: The systematic component of a generalized

linear model assumes the form

= g

−1

(β

+ β

+ ···+ β

)

or alternatively: g(μ

)=β

+ β

+ ···+ β

where g() (called a link function) is a monotonic, diﬀerentiable function

(such as a logarithm function). The randomness is explained by assuming

y has a distribution from a speciﬁc family of probability distributions

(which includes common distributions such as the normal, Poisson and

binomial as special cases). Generalized linear models are discussed from

Chap. 5 onwards. An example of a generalized linear model appears in

Example 1.5. Linear regression models are a special case of generalized

linear models.

The following notational conventions apply to regression models linear in the

parameters:

• The number of explanatory variables is p: x

, x

, ...x

• The number of regression parameters is denoted p



. If a constant term β

is in the systematic component (as is almost always the case) then p



p + 1, and the regression parameters are β

, β

, ...β

. If a constant term

is not in the systematic component then p



= p, and the regression

parameters are β

, β

, ...β

Example 1.3. For the lungcap data (Example 1.1,p.1), a possible systematic

component is given in (1.4) for some numerical values of β

, β

and

,fori =1, 2,...,654. This systematic relationship implies a linear rela-

tionship between μ and the covariates Age x

(which may be reasonable from

Fig. 1.1, top left panel), and Height x

, (which is probably not reasonable

from Fig. 1.1, top right panel). The model has p = 4 explanatory variables,

and p



= 5 unknown regression parameters.

One model for the random component, suggested in Sect. 1.5, was that

the variation of the observations about this systematic component was as-

sumed to be approximately constant, so that var[y

]=σ

. Combining the

two components, a possible linear regression model for modelling the fev is



var[y

]=σ

(random component)

= β

+ β

(systematic component).

(1.7)

Often the subscripts i are dropped for simplicity when there is no ambiguity.

The values of the parameters β

, β

(for the systematic component)

and σ

(for the random component) are unknown, and must be estimated.

14 1 Statistical Models

This is the model implied in Sect. 1.5, where it was noted that both the

systematic and random components in (1.7) are likely to be inappropriate for

these data (Fig. 1.1). 

Example 1.4. Some other possible systematic components involving fev (y),

age (x

), height (x

), gender (x

) and smoking status (x

) include:

μ = β

+ β

(1.8)

μ = β

+ β

(1.9)

μ = β

+ β

(1.10)

μ = β

+ β

log x

+ β

(1.11)

μ = β

+ β

(1.12)

1/μ = β

+ β

(1.13)

log μ = β

+ β

(1.14)

μ = β

+exp(β

) − exp(β

)+β

(1.15)

All these systematic components apart from (1.15) are linear in the param-

eters and could be used as the systematic component of a generalized linear

model. Only (1.8)–(1.12) could be used to specify a linear regression model.



Example 1.5. The noisy miner is a small but aggressive native Australian

bird. A study [11] of the habitats of the noisy miner recorded (Table 1.2; data

set: nminer) the abundance of noisy miners (that is, the number observed;

Minerab) in two hectare transects located in buloke woodland patches with

varying numbers of eucalypt trees (Eucs). To plot the data (Fig. 1.4), a small

amount of randomness is ﬁrst added in the vertical direction to avoid over

plotting, using jitter():

> data(nminer) # Load the data

> names(nminer) # Show the variables

[1] "Miners" "Eucs" "Area" "Grazed" "Shrubs" "Bulokes" "Timber"

[8] "Minerab"

> plot( jitter(Minerab) ~ Eucs, data=nminer, las=1, ylim=c(0, 20),

xlab="Number of eucalypts per 2 ha", ylab="Number of noisy miners" )

See ?nminer for more information about the data and the other variables.

The random component certainly does not have constant variance, as the

observations are more spread out for a larger numbers of eucalypts. Because

the responses are counts, a Poisson distribution with mean μ

for Observa-

tion i may be suitable for modelling the data. We write y

∼ Pois(μ

), where

> 0.

The relationship between μ and the number of eucalypts also seems non-

linear. A possible model for the systematic component is E[y

]=μ

exp(β

+ β

), where x

is the number of eucalypt trees at location i. This

1.6 Regression Models 15

Tabl e 1. 2 The number of eucalypt trees and the number of noisy miners observed in

two hectare transects in buloke woodland patches within the Wimmera Plains of western

Victoria, Australia (Example 1.5)

Number of Number of Number of Number of Number of Number of

eucalypts noisy miners eucalypts noisy miners eucalypts noisy miners

2 0 32 19 0 0

10 0 2 0 0 0

16 3 16 2 0 0

20 2 7 0 3 0

19 8 10 3 8 0

18 1 15 1 8 0

12 8 30 7 15 0

16 5 4 1 21 3

30 4 0244

12 4 19 7 15 6

11 0

0 5 10 15 20 25 30

Number of eucalypts per 2 ha

Number of noisy miners

Fig. 1.4 The number of noisy miners (observed in two hectare transects in buloke wood-

land patches within the Wimmera Plains of western Victoria, Australia) plotted against

the number of eucalypt trees. A small amount of randomness is added to the number of

miners in the vertical direction to avoid over-plotted observations (Example 1.5)

functional form ensures μ

> 0, as required for the Poisson distribution, and

may also be appropriate for modelling the non-linearity.

Combining the two components, one possible model for the data, dropping

the subscripts i,is:



y ∼ Pois(μ) (random component)

μ =exp(β

+ β

x) (systematic component)

(1.16)

where μ =E[y]. This is an example of a Poisson generalized linear model

(Chap. 10).

16 1 Statistical Models

We also note that one location (with 19 noisy miners) has more than twice

the number of noisy miners observed than the location with the next largest

number of noisy miners (with eight noisy miners). 

1.7 Interpreting Regression Models

Models are most useful when they have sensible interpretations. Compare

these two systematic components:

μ = β

+ β

x (1.17)

log μ = β

+ β

x. (1.18)

The ﬁrst model (1.17) assumes a linear relationship between μ and x,and

hence that an increase of one in the value of x is associated with an increase

of β

in the value of μ. The second model (1.18) assumes a linear relationship

between log μ and x, and hence that an increase of one in the value of x

will increase the value of log μ by β

. This implies that when the value of x

increases by one, μ increases (approximately) by a factor of exp(β

). To see

this, write the second systematic component (1.18)as

=exp(β

+ β

x) = exp(β

)exp(β

)

Hence if the value of x increases by 1, to x +1,wehave

x+1

=exp(β

)exp(β

)

x+1

= μ

exp(β

A researcher should consider which is more sensible for the application. Fur-

thermore, models that are based on underlying theory or sensible approxi-

mations to the problem (Sect. 1.10) produce models with better and more

meaningful interpretations. Note that the systematic component (1.17)is

suitable for a linear regression model, and that both systematic components

are suitable for a generalized linear model.

Example 1.6. For the lungcap data, consider a model relating fev y to

height x. Model (1.17) would imply that an increase in height of one inch is

associated with an increase in fev of β

L. In contrast, Model (1.18) would

imply that an increase in height of one inch is associated with an increase in

fev by a factor of exp(β

)L. 

A further consideration when interpreting models is when models con-

tain more than one explanatory variable. In these situations, the regression

parameters should be interpreted with care, since the explanatory variables

may not be independent. For example, for the lung capacity data, the age

and height of youth are related (Fig. 1.5): older youth are taller, on average:

1.8 All Models Are Wrong, but Some Are Useful 17

lll

llll

lll

llll

lll

llll

lll

llll

lllllll

lll

llll

lll

lllll

lll

llll

lll

llll

lll

llllll

lll

llllll

lllll

llll

lll

0 5 10 15 20

Females

Age (in years)

Height (in inches)

lll

llll

lll

llll

lll

llll

lllllll

llll

lll

lllll

lll

llll

llllll

llll

lll

llll

lllll

lll

llll

llllll

llll

lll

lllll

llll

lll

llll

lll

0 5 10 15 20

Males

Age (in years)

Height (in inches)

Fig. 1.5 A strong relationship exists between the height and the age of the youth in

the lung capacity data: females (left panel) and males (right panel)

> plot( Ht ~ Age, data=subset(lungcap, Gender=="F"), las=1,

ylim=c(45, 75), xlim=c(0, 20), # Use similar scales for comparisons

main="Females", xlab="Age (in years)", ylab="Height (in inches)" )

> plot( Ht ~ Age, data = subset(lungcap, Gender=="M"), las=1,

ylim=c(45, 75), xlim=c(0, 20), # Use similar scales for comparisons

main="Males", xlab="Age (in years)", ylab="Height (in inches)" )

In a model containing both age and height, it is not possible to interpret both

regression parameters independently, as expecting age to change while height

stays constant is unreasonable in youth. Note that height tends to increase

with age initially, then tends to stay similar as the youth stop (or slow) their

growing.

Further comments on model interpretation for speciﬁc models are given as

appropriate, such as in Sect. 2.7.

1.8 All Models Are Wrong, but Some Are Useful

Previous sections introduced regression models as a way to understand data.

However, when writing about statistical models, Box and Draper [2, p. 424]

declared “all models are wrong”. What do they mean? Were they correct? One

way to understand this is to contrast statistical models with some physical

models in common use. For example, biologists use models of the human skele-

ton to teach anatomy, which capture enough important information about the

real situation for the necessary purpose. Models are not an exact representa-

tion of reality: the skeleton is probably made of plastic, not bones; no-one may

have a skeleton with the exact dimensions of the model skeleton. However,

models are useful approximations for representing the necessary detail for

the purpose at hand.

18 1 Statistical Models

Similar principles apply to statistical models: they are mathematical ap-

proximations to reality that represent the important features of data for the

task at hand. The complete quote from Box and Draper clariﬁes [2, p. 424],

“. . . Essentially, all models are wrong, but some are useful. However, the ap-

proximate nature of the model must always be borne in mind”.

Despite the many similarities between physical and statistical models, two

important diﬀerences exist:

• A model skeleton shows the structure of an average or typical skeleton,

which is equivalent to the systematic component of a statistical model.

But no-one has a skeleton exactly like the model: some bones will be

longer, skinnier, or a diﬀerent shape. However, the model skeleton makes

no attempt to indicate the variation that is present in skeletons in the

population. The model skeleton ignores the variation from person to per-

son (the random component). In contrast, the statistical model represents

both the systematic trend and the randomness of the data. The random

component is modelled explicitly by making precise statements about the

random variation (Sect. 1.5).

• Most physical models are based on what is known to be true. Biolo-

gists know what a typical real skeleton looks like. Consequently, knowing

whether a physical model is adequate is generally easy, since the model

represents the important, known features of the true situation. However,

statistical models are often developed where the true model is unknown,

or is only artiﬁcially assumed to exist. In these cases, the model must be

developed from the available data.

1.9 The Purpose of a Statistical Model Aﬀects How It

Is Developed: Prediction vs Interpretation

The role of a statistical model is to accurately represent the important sys-

tematic and random features of the data. But what is the purpose of devel-

oping statistical models? For regression models, there are two major motiva-

tions:

• Prediction: To produce accurate predictions from new or future data.

• Understanding and interpretation: To understand how variables relate to

each other.

For example, consider the lung capacity study. The purpose of this study

may be to determine whether there is a (potentially causal) relationship be-

tween smoking and fev. Here we want to understand whether smoking has

an eﬀect on fev, and in what direction. For this purpose, the size and signif-

icance of coeﬃcients in the model are of interest. If smoking decreases lung

function, this would have implications for health policy.

1.10 Accuracy vs Parsimony 19

A diﬀerent health application is to establish the normal weight range for

children of a given age and gender. Here the purpose is to be able to judge

whether a particular child is out of the normal range, in which case some

intervention by health carers might be appropriate. In this case, a prediction

curve relating weight to age is desired, but the particular terms in the model

would not be of interest. The lung capacity data is in fact an extract from

a larger study [19] in which the pulmonary function of the same children

was measured at multiple time points (a longitudinal study), with the aim of

establishing the normal range for fev at each age.

Being aware of the major purpose of a study may aﬀect how a regression

model is ﬁtted and developed. If the major purpose is interpretation, then

it is important that all terms are reliably estimated and have good support

from the data. If the major purpose is prediction, then any predictor that

improves the precision of prediction may be included in the model, even if the

causal relationship between the predictor and the response is obscure or if

the regression coeﬃcient is relatively uncertain. This means that sometimes

one might include more terms in a regression model when the purpose is

prediction than when the purpose is interpretation and understanding.

1.10 Accuracy vs Parsimony

For any set of data, there are typically numerous systematic components that

could be chosen and various random components may also be possible. How

do we choose a statistical model from all the possible options?

Sometimes, statistical models are based on underlying theory, or from an

understanding of the physical features of the situation, and are built with

this knowledge in mind. In these situations, the statistical model may be

critiqued by how well the model explains the known features of the theoretical

situation.

Sometimes, approximations to the problem can guide the choice of model.

For example, for the lung capacity data, consider lungs roughly as cylinders,

whose heights are proportional to the height of the child, and assume the fev

is proportional to lung volume. Then volume ∝ (radius)

may be a suitable

model. This approach implies fev is proportional to x

,asinModels(1.8)–

(1.11)(p.14).

Sometimes, statistical models are based on data, often without guiding

theory, and no known ‘true’ state exists with which to compare. After all,

statistical models are artiﬁcial, mathematical constructs. The model is a rep-

resentation of an unknown, but assumed, underlying true state. How can we

know if the statistical model is adequate?

20 1 Statistical Models

In general, an adequate statistical model balances two criteria:

• Accuracy: The model should accurately describe both the systematic and

random components.

• Parsimony: The model should be as simple as possible.

According to the principle of parsimony (or Occam’s Razor), the simplest

accurate model is the preferred model. In other words, prefer the simplest

accurate model not contradicting the data. A model too simple or too complex

does not model the data well. Complex models may ﬁt the given data well but

usually do not generalize well to other data sets (this is called over-ﬁtting).

Example 1.7. Figure 1.6 (top left panel) shows the systematic component of

a linear model (represented by the solid line) ﬁtted to some data. This model

does not represent the systematic trend of the data. The variation around this

linear model is large and not random: observations are consistently smaller

than the ﬁtted model, then consistently larger, then smaller.

The systematic component of the ﬁtted cubic model (Fig. 1.6, top centre

panel) represents the systematic trend of the data, and suggests a small

amount of random variation about this trend.

The ﬁtted 10th order polynomial (Fig. 1.6, top right panel) suggests a small

amount of randomness, as the polynomial passes close to every observation.

However, the systematic polynomial component incorrectly represents both

the systematic and random components in the data. Because the systematic

component also represents the randomness, predictions based on this model

are suspect (predictions near x = −1 are highly dubious, for example).

The principle of parsimony suggests the cubic model is preferred. This

model is simple, accurate, and does not contradict the data. Researchers

focused only on producing a model passing close to each observation (and

hence selecting the 10th order polynomial) have a poor model. This is called

over-ﬁtting.

The data were actually generated from the model



y ∼ N(μ, 0.35)

μ = x

− 3x +5.

The notation y ∼ N(μ, 0.35) means the responses come from a normal dis-

tribution with mean μ and variance σ

=0.35.

Suppose new data were observed from this same true model (for example,

from a new experiment or from a new sample), and linear, cubic and 10th

order polynomial models were reﬁtted to this new data (Fig. 1.6, bottom

panels). The new ﬁtted linear model (Fig. 1.6, bottom left panel) still does

not ﬁt the data well. The new ﬁtted 10th order polynomial (Fig. 1.6, bottom

right panel) is very diﬀerent compared to the one ﬁtted to the ﬁrst data

set, even though the data for both were generated from the same model.

In contrast, the new ﬁtted cubic model (Fig. 1.6, bottom centre panel) is

very similar for both data sets, suggesting the cubic model represents the

systematic and random components well. 

1.11 Experiments vs Observational Studies: Causality vs Association 21

−2 −1 0 1 2

Linear:

Original data

−2 −1 0 1 2

Cubic:

Original data

−2 −1 0 1 2

10th order polynomial:

Original data

−2 −1 0 1 2

Linear:

New data

−2 −1 0 1 2

Cubic:

New data

−2 −1 0 1 2

10th order polynomial:

New data

Fig. 1.6 Three diﬀerent systematic components for an artiﬁcial data set. Left panels:

the data modelled using a linear model; centre panels: using a cubic model; right panels:

using a 10th order polynomial. The lines represent the systematic component of the ﬁtted

model. The top panels show the models ﬁtted to some data; the bottom panels shows the

models ﬁtted to data randomly generated from the same model used to generate the data

in the top panels. A good model would be similar for both sets of data (Example 1.7)

1.11 Experiments vs Observational Studies: Causality

vs Association

All models must be used and understood within limitations imposed by how

the data were collected. The method of data collection inﬂuences the con-

clusions that can be drawn from the analysis. An important aspect of this

concerns whether researchers intervene to apply treatments to subjects or

simply observe pre-existing processes.

In an observational study, researchers may use elaborate equipment to

collect physical measures or may ask subjects to respond to carefully de-

signed questionnaires, but do not inﬂuence the processes being observed.

22 1 Statistical Models

Observational studies generally only permit conclusions about associations

between variables, not a cause-and-eﬀect. While the relationship may in fact

be causal, the use of observational data by itself it not usually suﬃcient to

conﬁrm this conclusion. In contrast, researchers conducting a designed ex-

periment do intervene to control the values of the explanatory variables that

appear in the data. The distinguishing feature of an experiment versus an

observational study is that the researchers conducting the study are able to

determine which experimental condition is applied to each subject. A well-

designed randomized experiment allows inference to be made about cause-

and-eﬀect relationships between the explanatory and response variables.

Statistical models treat experimental and observational studies in the same

way, and the statistical conclusions are superﬁcially similar, but scientiﬁc

conclusions from experiments are usually much stronger. In an observational

study, the best that can be done is to measure all other extraneous variables

that are likely to aﬀect the response, so that the analysis can adjust for as

many uncontrolled eﬀects as possible. In this way, good quality data and

careful statistical analysis can go a long way towards correcting for many

inﬂuences that cannot be controlled in the study design.

Example 1.8. The lung capacity data (Example 1.1) is a typical observational

study. The purpose of the study is to explore the eﬀects of smoking on lung

capacity, as measured by fev (explored later in Problem 11.15). Whether or

not each participant is a smoker is out of the control of the study designers,

and there are many physical characteristics, such as age and height, that

have direct eﬀects on lung capacity, and some quite probably have larger

eﬀects than the eﬀect of interest (that of smoking). Hence it was necessary

to record information on the height, age and gender of participants (which

become extraneous variables) so that the inﬂuence of these variables can be

taken into account. The aim of the analysis therefore is to try to measure the

association between smoking and lung capacity after adjusting for age, height

and gender. It is always possible that there are other important variables that

inﬂuence fev that have not been measured, so any association discovered

between fev and smoking should not be assumed to be cause-and-eﬀect. 

1.12 Data Collection and Generalizability

Another feature of data collection that aﬀects conclusions is the population

from which the subjects or cases are drawn. In general, conclusions from

ﬁtting and analysing a statistical model only apply to the population from

which the cases are drawn. So, for example, if subjects are drawn from women

aged over 60 in Japan, then conclusions do not necessarily apply to men, to

women in Japan aged under 60, or to women aged over 60 elsewhere.

1.13 Using R for Statistical Modelling 23

Similarly, the conclusions from a regression model cannot necessarily be

applied (extrapolated) outside the range of the data used to build the model.

Example 1.9. The lung capacity data (Example 1.1) is from a sample of

youths from the middle to late 1970s in Boston. Using the results to infer

information about other times and locations may or may not be appropri-

ate. The study designers might hope that Boston is representative of much

of the United States in terms of smoking among youth, but generalizing the

results to other countries with diﬀerent lifestyles or to the present day may

be doubtful.

The youths in the fev study are aged from 3 to 19. As no data exists

outside this age range, no statistical model can be veriﬁed to apply outside

this age range. In the same way, no statistical model applies for youth under

46 inches tall or over 74 inches tall. fev cannot be expected to increase

linearly for all ages and heights. 

1.13 Using R for Statistical Modelling

A computer is indispensable in any serious statistical work for performing the

necessary computations (such as estimating the values of β

), for producing

graphics, and for evaluating the ﬁnal model.

Although the theory and applications of glms discussed throughout this

book apply generally, the implementation is possible in various statistical

computer packages. This book discusses how to perform these analyses using

r (all computations in this book are performed in r version 3.4.3). A short

introduction to using r is given in Appendix A (p. 503).

This section summarizes and collates some of the relevant r commands

introduced in this chapter. For more information on some command foo,

type ?foo at the r command prompt.

• library(): Loads extra r functionality that is contained in an r package.

For example, use library(GLMsData) to make the data frames associated

with this book available in r. See Appendix B (p. 525) for information

about obtaining and installing this package.

• data(): Loads data frames.

• names(x): Lists the names of the variables in the data frame x.

• summary(object): Produces a summary of the variable object,orofthe

data frame object.

• factor(x): Declares x as a factor. The ﬁrst input is the variable to be

declared as a factor. Two further inputs are optional. The second (op-

tional) input levels is the list of the levels of the factor; by default the

levels of the factor are sorted by numerical or alphabetical order. The

third (optional) input labels gives the labels to assign to the levels of

the factor in the order given by levels (or the order assumed by default).

24 1 Statistical Models

• relevel(x, ref): Changes the reference level for factor x. The ﬁrst in-

put is the factor, and the second input ref is the level of the factor to

use as the reference level.

• plot(): Plots data. See Appendix A.3.10 (p. 516) for more information.

• legend(): Adds a legend to a plot.

1.14 Summary

Chapter 1 introduces the idea of a statistical model. In this context, y refers

to the response variable, n to the number of observations, and x

,...,x

to the p explanatory variables. Quantitative explanatory variables are called

covariates; qualitative explanatory variables are called factors (Sect. 1.2). Fac-

tors must be coded numerically for use in statistical models (Sect. 1.4)using

dummy variables. Treatment codings are commonly used, and are used by

default in r. k − 1 dummy variables are required for a factor with k levels.

Plots are useful for an initial examination of data (Sect. 1.3), but statistical

models are necessary for better understanding. Statistical models explain the

two components of data: The systematic component models how the mean

response changes as the explanatory variables change; the random component

models the variation of the data about the mean (Sect. 1.5). In this way,

statistical models represent both the systematic and random components

of data (Sect. 1.8), and can be used for prediction, and for understanding

relationships between variables (Sect. 1.9). Two criteria exist for an adequate

model: simplicity and accuracy. The simplest model that accurately describes

the systematic component and the randomness is preferred (Sect. 1.10).

Regression models ‘linear in the parameters’ have a systematic component

of the form E[y

]=μ

= f(β

+β

+···+β

) (Sect. 1.6). In these models,

the number of regression parameters is denoted p



. If a constant term β

in the systematic component, as is almost always the case, then p



= p +1;

otherwise p



= p (Sect. 1.6).

Statistical models should be able to be sensibly interpreted (Sect. 1.7).

However, ﬁtted models should be interpreted and understood within the lim-

itations of the data and of the model (Sect. 1.11). For example: in observa-

tional studies, data are simply observed, and no cause-and-eﬀects conclusions

can be drawn. In experimental studies, data are produced when the researcher

has some control over the values of at least some of the explanatory variables

to use; cause-and-eﬀect conclusions may be drawn (Sect. 1.11). In general,

conclusions from ﬁtting and analysing a statistical model only apply to the

population represented by the sample (Sect. 1.12).

Computers are invaluable in statistical modelling, especially for estimating

parameters and graphing (Sect. 1.13).

1.14 Summary 25

Problems

Selected solutions begin on p. 529.

1.1. The plots in Fig. 1.7 (data set: paper) show the strength of Kraft pa-

per [7, 8] for diﬀerent percentages of hardwood concentrations. Which sys-

tematic component, if any, appears most suitable for modelling the data?

Explain.

1.2. The plots in Fig. 1.8 (data set: heatcap) show the heat capacity of solid

hydrogen bromide y measured as a function of temperature x [6, 16]. Which

systematic component, if any, appears best for modelling the data? Explain.

1.3. Consider the data plotted in Fig. 1.9. In the panels, quadratic, cubic and

quartic systematic components are shown with the data. Which systematic

component appears best for modelling the data? Explain.

The data are actually randomly generated using the systematic component

μ =1+10exp(−x/2) (with added randomness), which is not a polynomial

at all. Explain what this demonstrates about ﬁtting systematic components.

1.4. Consider the data plotted in Fig. 1.10 (data set: toxo). The data show

the proportion of the population y testing positive to toxoplasmosis against

the annual rainfall x for 34 cities in El Salvador [5]. Analysis suggests a cubic

model ﬁts the data reasonably well (though substantial variation still exists).

What important features of the data are evident from the plot? Which of the

plotted systematic components appears better? Explain.

1.5. For the following systematic components used in a regression model,

determine if they are appropriate for regression models linear in the parame-

ters, linear regression models, and/or generalized linear models. In all cases,

refers to model parameters, μ is the expected value of the response vari-

able, while x, x

and x

refer to explanatory variables.

0 5 10 15

Quadratic in % hardwood

Percent hardwood

Strength

0 5 10 15

Cubic in % hardwood

Percent hardwood

Strength

0 5 10 15

Quartic in % hardwood

Percent hardwood

Strength

Fig. 1.7 Three diﬀerent systematic components for the Kraft paper data set: ﬁtted

quadratic, cubic and quartic systematic components are shown (Problem 1.1)

26 1 Statistical Models

120 140 160 180

10.5

11.0

11.5

12.0

12.5

Linear in temperature

Temperature (in Kelvin)

Heat capacity (cal/(mol K))

120 140 160 180

10.5

11.0

11.5

12.0

12.5

Quadratic in temperature

Temperature (in Kelvin)

Heat capacity (cal/(mol K))

120 140 160 180

10.5

11.0

11.5

12.0

12.5

Cubic in temperature

Temperature (in Kelvin)

Heat capacity (cal/(mol K))

120 140 160 180

10.5

11.0

11.5

12.0

12.5

Quartic in temperature

Temperature (in Kelvin)

Heat capacity (cal/(mol K))

Fig. 1.8 Plots of the heat capacity data: ﬁtted linear, quadratic, cubic and quartic

systematic components are shown (Problem 1.2)

0246810

Quadratic model

x data

y data

0246810

Cubic model

x data

y data

0246810

Quartic model

x data

y data

Fig. 1.9 Three diﬀerent systematic components for a data set: ﬁtted quadratic, cubic

and quartic systematic components are shown (Problem 1.3)

1. μ = β

+ β

log x

2. μ = β

+exp(β

+ β

x).

3. μ =exp(β

+ β

x)forμ>0.

4. μ =1/(β

+ β

)forμ>0.

1.14 Summary 27

1400 1800 2200 2600

0.0

0.2

0.4

0.6

0.8

1.0

A cubic regression model

Annual rainfall (mm)

Proportion testing positive

1400 1800 2200 2600

0.0

0.2

0.4

0.6

0.8

1.0

A cubic glm

Annual rainfall (mm)

Proportion testing positive

Fig. 1.10 The toxoplasmosis data, and two ﬁtted cubic systematic components

(Problem 1.4)

1.6. Load the data frame turbines from the package GLMsData. Brieﬂy, the

data give the proportion of turbines developing ﬁssures after a given number

of hours of run-time [13, 14].

1. Use names() to determine the names of the variables in the data frame.

2. Determine which variables are quantitative and which are qualitative.

3. For any qualitative variables, deﬁne appropriate dummy variables using

treatment coding.

4. Use r to summarize each variable.

5. Use r to create a plot of the proportion of failures (turbines with ﬁssures)

against run-time.

6. Determine the important features of the data evident from the plot.

7. Would a linear regression model seem appropriate for modelling the data?

Explain.

8. Read the help for the data frame (use ?turbines after loading the

GLMsData package in r), and determine whether the data come from

an observational or experimental study, then discuss the implications.

1.7. Load the data frame humanfat. Brieﬂy, the data record the percentage

body fat y, age, gender and body mass index (bmi) of 18 adults [12]. The

relationship between y and bmi is of primary interest.

1. Use names() to determine the names of the variables in the data.

2. Determine which variables are quantitative and which are qualitative.

Identify which variables are extraneous variables.

3. For any qualitative variables, deﬁne appropriate dummy variables using

treatment coding.

4. Use r to summarize each variable.

28 1 Statistical Models

5. Plot the response against each explanatory variable, and discuss any im-

portant features of the data.

6. Would a linear regression model seem appropriate for modelling the data?

Explain.

7. Read the help for the data frame (use ?humanfat after loading the

GLMsData package in r), and determine whether the data come from

an experiment or observational study. Explain the implications.

8. After reading the help, determine the population to which the results can

be expected to generalize.

9. Suppose a linear regression model was ﬁtted to the data with systematic

component μ = β

+ β

, where x

is bmi. Interpret the systematic

component of this model.

10. Suppose a generalized linear model was ﬁtted to the data with system-

atic component log μ = β

+ β

, where x

is bmi,andx

is 0

for females and 1 for males. Interpret the systematic component of this

model.

11. For both models given above, determine the values of p and p



1.8. Load the data frame hcrabs. Brieﬂy, the data give the number of male

satellite crabs y attached to female horseshoe crabs of various weights (in g),

widths (in cm), colours and spine conditions [1, 3].

1. Determine which variables are quantitative and which are qualitative.

2. For any qualitative variables, deﬁne appropriate dummy variables using

treatment coding.

3. Use r to summarize each variable.

4. Produce appropriate plots to help understand the data.

5. Find the correlation between weight and width, and comment on the

implications.

6. Read the help for the data frame (use ?hcrabs after loading package

GLMsData in r), and determine whether the data come from an exper-

iment or observational study. Explain the implications.

7. After reading the help, determine the population to which the results can

be expected to generalize.

8. Suppose a linear regression model was ﬁtted to the data with systematic

component μ = β

+ β

, where x

is the weight of the crab. Interpret

the systematic component of this model. Comment on the suitability of

the model.

9. Suppose a generalized linear model was ﬁtted to the data with systematic

component log μ = β

+β

, where x

is the weight of the crab. Interpret

the systematic component of this model. Comment on the suitability of

the model.

10. For the model given above, determine the values of p and p



1.9. Children were asked to build towers as high as they could out of cubical

and cylindrical blocks [9, 17]. The number of blocks used and the time taken

were recorded.

REFERENCES 29

1. Load the data frame blocks from the package GLMsData, and produce

a summary of the variables.

2. Produce plots to examine the relationship between the time taken to

build towers, and the block type, trial number, and age.

3. In words, summarize the relationship between the four variables.

4. Produce plots to examine the relationship between the number of blocks

used to build towers, and the block type, trial number, and age.

5. Summarize the relationship between the four variables in words.

1.10. In a study of foetal size [15], the mandible length (in mm) and gesta-

tional age for 167 foetuses were measured from the 15th week of gestation

onwards. Load the data frame mandible from the package GLMsData, then

use r to create a plot of the data.

1. Determine the important features of the data evident from the plot.

2. Is a linear relationship appropriate? Explain.

3. Is a model assuming constant variation appropriate? Explain.

References

[1] Agresti, A.: An Introduction to Categorical Data Analysis, second edn.

Wiley-Interscience (2007)

[2] Box, G.E.P., Draper, N.R.: Empirical Model-Building and Response Sur-

faces. Wiley, New York (1987)

[3] Brockmann, H.J.: Satellite male groups in horseshoe crabs, limulus

polyphemus. Ethology 102, 1–21 (1996)

[4] Dunn, P.K., Smyth, G.K.: GLMsData: Generalized linear model data

sets (2017). URL https://CRAN.R-project.org/package=GLMsData.R

package version 1.0.0

[5] Efron, B.: Double exponential families and their use in generalized linear

regression. Journal of the American Statistical Association 81(395), 709–

721 (1986)

[6] Giauque, W.F., Wiebe, R.: The heat capacity of hydrogen bromide from

◦

K. to its boiling point and its heat of vaporization. The entropy from

spectroscopic data. Journal of the American Chemical Society 51(5),

1441–1449 (1929)

[7] Hand, D.J., Daly, F., Lunn, A.D., McConway, K.Y., Ostrowski, E.: A

Handbook of Small Data Sets. Chapman and Hall, London (1996)

[8] Joglekar, G., Scheunemyer, J.H., LaRiccia, V.: Lack-of-ﬁt testing when

replicates are not available. The American Statistician 43, 135–143

(1989)

[9] Johnson, B., Courtney, D.M.: Tower building. Child Development 2(2),

161–162 (1931)

30 REFERENCES

[10] Kahn, M.: An exhalent problem for teaching statistics. Journal of Sta-

tistical Education 13(2) (2005)

[11] Maron, M.: Threshold eﬀect of eucalypt density on an aggressive avian

competitor. Biological Conservation 136, 100–107 (2007)

[12] Mazess, R.B., Peppler, W.W., Gibbons, M.: Total body composition

by dualphoton (

153

Gd) absorptiometry. American Journal of Clinical

Nutrition 40, 834–839 (1984)

[13] Myers, R.H., Montgomery, D.C., Vining, G.G.: Generalized Linear Mod-

els with Applications in Engineering and the Sciences. Wiley, Chichester

(2002)

[14] Nelson, W.: Applied Life Data Analysis. Wiley Series in Probability and

Statistics. John Wiley Sons, New York (1982)

[15] Royston, P., Altman, D.G.: Regression using fractional polynomials of

continuous covariates: Parsimonious parametric modelling. Journal of

the Royal Statistical Society, Series C 43(3), 429–467 (1994)

[16] Shacham, M., Brauner, N.: Minimizing the eﬀects of collinearity in poly-

nomial regression. Industrial and Engineering Chemical Research 36,

4405–4412 (1997)

[17] Singer, J.D., Willett, J.B.: Improving the teaching of applied statistics:

Putting the data back into data analysis. The American Statistician

44(3), 223–230 (1990)

[18] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

[19] Tager, I.B., Weiss, S.T., Muñoz, A., Rosner, B., Speizer, F.E.: Longitu-

dinal study of the eﬀects of maternal smoking on pulmonary function in

children. New England Journal of Medicine 309(12), 699–703 (1983)

[20] Tager, I.B., Weiss, S.T., Rosner, B., Speizer, F.E.: Eﬀect of parental

cigarette smoking on the pulmonary function of children. American

Journal of Epidemiology 110(1), 15–26 (1979)

Chapter 2

Linear Regression Models

Almost all of statistics is linear regression, and most of

what is left over is non-linear regression.

Robert Jennrich, in the discussion of Green [4, p. 182]

2.1 Introduction and Overview

The most common of all regression models is the linear regression model,

introduced in this chapter. This chapter also introduces the notation and

language used in this book so a common foundation is laid for all readers

for the upcoming study of generalized linear models: linear regression models

are a special case of generalized linear models. We ﬁrst deﬁne linear regres-

sion models and introduce the relevant notation and assumptions (Sect. 2.2).

We then describe least-squares estimation for simple linear regression models

(Sect. 2.3) and multiple regression models (Sects. 2.4 and 2.5). The use of the

r functions to ﬁt linear regression models is explained in Sect. 2.6, followed

by a discussion of the interpretation of linear regression models (Sect. 2.7).

Inference procedures are developed for the regression coeﬃcients (Sect. 2.8),

followed by analysis of variance methods (Sect. 2.9). We then discuss meth-

ods for comparing nested models (Sect. 2.10), and for comparing non-nested

models (Sect. 2.11). Tools to assist in model selection are then described

(Sect. 2.12).

2.2 Linear Regression Models Deﬁned

In this chapter, we consider linear regression models for modelling data with

a response variable y and p explanatory variables x

, x

, ..., x

. A linear

regression model consists of the usual two components of a regression model

(random and systematic components), with speciﬁc forms.

The random component assumes that the responses y

have constant vari-

ances σ

, or that the variances are proportional to known, positive weights

;thatis,var[y

]=σ

for i =1, 2,...n.Thew

are called prior weights,

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_2

32 2 Linear Regression Models

which provide the possibility of giving more weight to some observations than

to others. The systematic component assumes that the expected value of the

response E[y

]=μ

is linearly related to the explanatory variables x

such

that μ

= β



j=1

Combining these components, a linear regression model has the general

form

⎧

⎪

⎨

⎪

⎩

var[y

]=σ

= β



j=1

(2.1)

where E[y

]=μ

, and the prior weights w

are known. The regression param-

eters β

,β

,...,β

, as well as the error variance σ

, are unknown and must

be estimated from the data. Recall, the number of regression parameters for

Model (2.1)isp



= p +1. β

is often called the intercept, since it is the value

of y when all the explanatory variables are zero. The parameters β

,...β

are sometimes called the slopes for the corresponding explanatory variables.

A linear regression model with systematic component μ = β

+ β

(that

is, p =1andp



= 2) is called a simple linear regression model or a simple

regression model. A linear regression model with all prior weights w

set to

one is called an ordinary linear regression model, to be distinguished from a

weighted linear regression model when the prior weights are not all one. A

linear regression model with p>1 is often called a multiple linear regression

model or multiple regression model. Figure 2.1 shows how the systematic and

random components combine to specify the model in the case of simple linear

regression with all prior weights set to one.

The assumptions necessary for establishing Model (2.1)are:

• Suitability: The same regression model is appropriate for all the observa-

tions.

• Linearity: The true relationship between μ and each quantitative explana-

tory variable is linear.

• Constant variance: The unknown part of the variance of the responses,

,isconstant.

• Independence: The responses y are independent of each other.

Example 2.1. The mean birthweight y (in kg) and gestational ages x (in

weeks) of 1513 infants born to Caucasian mothers at St George’s hospital,

London, between August 1982 and March 1984 [2] were recorded from vol-

unteers (Table 2.1; data set: gestation).

> library(GLMsData); data(gestation); str(gestation)

'data.frame': 21 obs. of 4 variables:

$ Age : int 22 23 25 27 28 29 30 31 32 33 ...

$ Births: int 1111613677...

$ Weight: num 0.52 0.7 1 1.17 1.2 ...

$ SD : num NA NA NA NA 0.121 NA 0.589 0.319 0.438 0.313 ...

> summary(gestation) # Show the first few lines of the data

2.2 Linear Regression Models Deﬁned 33

0 5 10 15 20

Fig. 2.1 A simple linear regression model, with all prior weights set to 1. The points

show the observations, and the solid dark line shows the values of μ from the linear

relationship (the systematic component). The arrows and dotted lines indicate that the

variation (random component) is approximately constant for all values of x (Sect. 2.2)

Tabl e 2.1 Mean birthweights and gestational ages of babies born to Caucasian mothers

at St George’s hospital, London, between August 1982 and March 1984 who were willing

to participate in the research (Example 2.1)

Gestational Number Birthweight Gestational Number Birthweight

age (weeks) of births means (kg) age (weeks) of births means (kg)

22 1 0.520 35 29 2.796

23 1 0.700 36 43 2.804

25 1 1.000 37 114 3.108

27 1 1.170 38 222 3.204

28 6 1.198 39 353 3.353

29 1 1.480 40 401 3.478

30 3 1.617 41 247 3.587

31 6 1.693 42 53 3.612

32 7 1.720 43 9 3.390

33 7 2.340 44 1 3.740

34 7 2.516

Age Births Weight SD

Min. :22.00 Min. : 1.00 Min. :0.520 Min. :0.1210

1st Qu.:29.00 1st Qu.: 1.00 1st Qu.:1.480 1st Qu.:0.3575

Median :34.00 Median : 7.00 Median :2.516 Median :0.4270

Mean :33.76 Mean : 72.05 Mean :2.335 Mean :0.4057

3rd Qu.:39.00 3rd Qu.: 53.00 3rd Qu.:3.353 3rd Qu.:0.4440

Max. :44.00 Max. :401.00 Max. :3.740 Max. :0.5890

NA's :6

34 2 Linear Regression Models

20 25 30 35 40 45

Gestational age (weeks)

Mean birthweight (kg)

Fig. 2.2 A plot of mean birthweights against gestational ages from Table 2.1.The

hollow dots are used for the means based on fewer than 20 observations, and ﬁlled dots

for other observations (Example 2.1)

The mean birthweight (Weight) and standard deviation of birthweights (SD)

of all the babies at given gestational ages are recorded. Notice the appearance

of NA in the data; NA means ‘not available’. Here the NAs appear because

standard deviations cannot be computed for gestational ages where only one

birth was recorded.

The relationship between the expected mean birthweight of babies μ =

E[y] and gestational age x is approximately linear over the given gestational

age range (Fig. 2.2):

> plot( Weight ~ Age, data=gestation, las=1, pch=ifelse( Births<20, 1, 19),

xlab="Gestational age (weeks)", ylab="Mean birthweight (kg)",

xlim=c(20, 45), ylim=c(0, 4))

The construct pch=ifelse(Births<20, 1, 19) means that if the number

of births m is fewer than 20, then plot using pch=1 (an empty circle), and

otherwise use pch=19 (a ﬁlled circle).

Note that, for example, there are m = 3 babies born at x = 30 weeks

gestation. This means that three observations have been combined to make

this entry in the data, so this information should be weighted accordingly.

There are n = 21 rows in the data frame (and 21 gestational ages given), but

a total of



i=1

= 1513 births are represented.

The responses y

here represent sample mean birthweights. If birthweights

of individual babies at gestational age x

have variance σ

, then expect the

sample means y

to have variance σ

, where m

is the sample size of

group i. A sensible random component is var[y

]=σ

, so that the known

prior weights are w

= m

. A possible model for the data is



var[y

]=σ

= β

+ β

(2.2)

2.3 Simple Linear Regression 35

Model (2.2) is a weighted linear regression model. Mean birthweights based

on larger numbers of observations contain more information than mean birth-

weights based on smaller numbers of observations. Using prior weights enables

the observations to be suitably weighted to reﬂect this. 

2.3 Simple Linear Regression

2.3.1 Least-Squares Estimation

Many of the principles of linear regression can be seen in the case of simple

linear regression, when there is only an intercept and a single covariate in the

model; that is,



var[y

]=σ

= β

+ β

where E[y

]=μ

For regression models to be used in practice, estimates of the intercept β

and slope β

are needed, as well as the variance σ

. For any given intercept

and slope, the deviations between the observed data y

and the model μ

are

given by

= y

− μ

= y

− β

. (2.3)

It makes sense to choose the ﬁtted line (that is, the estimates of β

and β

)

in such a way as to make the deviations as small as possible. To summarize

the deviations, we can square them (to avoid negative quantities) then sum

them, to get

S(β

,β



i=1



i=1

− μ

)



i=1

− β

)

The non-negative weights w

may be used to weight observations according to

their precision (for example, mean birthweights based on larger sample sizes

are estimated with greater precision, so can be allocated larger weights). S

summarizes how far the ﬁtted line is from the observations y

. Smaller values

of S mean the line is closer to the y

, in general. The least-squares principle

is to estimate β

and β

by those values that minimize S.

Example 2.2. Consider the gestation data from Example 2.1. We can try

some values for β

and β

, and compute the corresponding value of S.

> y <- gestation$Weight

> x <- gestation$Age

> wts <- gestation$Births

> beta0.A <- -0.9; beta1.A <- 0.1 # Try these values for beta0 and beta1

> mu.A <- beta0.A + beta1.A * x

> SA <- sum( wts*(y - mu.A)^2 ); SA

[1] 186.1106

36 2 Linear Regression Models

20 25 30 35 40 45

Age (years)

Weight (grams)

S = 186.1

μ=−0.9 + 0.1x

20 25 30 35 40 45

Age (years)

Weight (grams)

S = 343.4

μ=−3 + 0.15x

20 25 30 35 40 45

Age (years)

Weight (grams)

S = 11.42

= −2.678 + 0.1538x

Fig. 2.3 Three possible systematic components relating weight and age. For three ob-

servations, the deviations from the postulated equation are shown by thin vertical lines

(Example 2.2)

This shows that the values β

= −0.9andβ

=0.1 produce S = 186.1

(Fig. 2.3, left panel). Suppose we try diﬀerent values for β

and β

> beta0.B <- -3; beta1.B <- 0.150

> mu.B <- beta0.B + beta1.B * x

> SB <- sum( wts*(y - mu.B)^2 ); SB

[1] 343.4433

Using β

= −3andβ

=0.15 produces S = 343.4 (centre panel), so the

values of β

and β

used in the left panel are preferred over those used in the

centre panel.

The smallest possible value for S is achieved using the least-squares esti-

mates

and

(right panel). 

2.3.2 Coeﬃcient Estimates

The least-squares estimators of β

and β

can be found by using calculus to

minimize the sum of squares S(β

,β

). The derivatives of S with respect to

and β

are

∂S(β

,β

)

∂β



i=1

− μ

); (2.4)

∂S(β

,β

)

∂β



i=1

− μ

). (2.5)

2.3 Simple Linear Regression 37

Solving ∂S/∂β

= ∂S/∂β

= 0 (Problem 2.2) gives the following solutions

for β

and β

=¯y

−

¯x

; (2.6)



i=1

− ¯x



i=1

− ¯x

)

, (2.7)

where ¯x

and ¯y

are the weighted means

¯x



i=1



i=1

and ¯y



i=1



i=1

Here

and

are the least-squares estimators of β

and β

respectively.

They can be shown to be unbiased estimators of β

and β

respectively

(Problem 2.5). The ﬁtted values are estimated by ˆμ

,fori =

1,...,n.

The minimized value of S(β

,β

), evaluated at the least-squares estimates

and β

, is called the residual sum-of-squares (rss):

rss =



i=1

− ˆμ

)



i=1

−

)

, (2.8)

because r

= y

− ˆμ

are called the raw residuals. (Contrast this with the

deviations given in (2.3).)

Example 2.3. For the gestation data model (2.2), the least-squares param-

eter estimates can be computed using (2.6) and (2.7):

> xbar <- weighted.mean(x, w=wts) # The weighted mean of x (Age)

> SSx <- sum( wts*(x-xbar)^2 )

> ybar <- weighted.mean(y, w=wts) # The weighted mean of y (Weight)

> SSxy <- sum( wts*(x-xbar)*y )

> beta1 <- SSxy / SSx; beta0 <- ybar - beta1*xbar

> mu <- beta0 + beta1*x

> RSS <- sum( wts*(y - mu )^2 )

> c( beta0=beta0, beta1=beta1, RSS=RSS )

beta0 beta1 RSS

-2.6783891 0.1537594 11.4198322

This is not how the model would be ﬁtted in r in practice, but we proceed

this way to demonstrate the formulae above. The usual way to ﬁt the model

(see Sect. 2.6) would be to use lm():

> lm(Weight ~ Age, weights=Births, data=gestation)

Call:

lm(formula = Weight ~ Age, data = gestation, weights = Births)

Coefficients:

(Intercept) Age

-2.6784 0.1538

38 2 Linear Regression Models

Either way, the systematic component of the model is estimated as

ˆμ = −2.678 + 0.1538x (2.9)

with rss =11.42. 

2.3.3 Estimating the Variance σ

By deﬁnition, σ

=var[y

]=E[(y

− μ

)

], so it is reasonable to try to

estimate σ

by the average of the squared deviations w

−ˆμ

)

= rss. This

leads to the superﬁcially attractive proposal of estimating σ

ˆσ

rss

If the μ

were known and not estimated (by ˆμ

), this would be an ideal es-

timator. Unfortunately the process of estimating ˆμ

is based on minimizing

rss, making rss smaller than it would be by random variation and introduc-

ing a negative bias into ˆσ

. In other words, ˆσ

is a biased estimate of σ

.The

correct way to adjust for the fact that the regression parameters have been

estimated is to divide by n − 2 instead of n. This leads to

rss

n − 2

. (2.10)

This is an unbiased estimator of σ

, and is the estimator almost always used

in practice.

The divisor n − 2 here is known as the residual degrees of freedom.The

residual degrees of freedom are equal to the number of observations minus

the number of coeﬃcients estimated in the systematic component of the lin-

ear regression model. One can usefully think of the process of estimating

each coeﬃcient as “using up” the equivalent of one observation. For simple

linear regression, there are two coeﬃcients needing to be estimated, so that

the equivalent of only n − 2 independent observations remain to estimate

the variance. The terminology degrees of freedom arises from the following

observation. If the ﬁrst n − 2 values of r

= y

−

were known, then

the remaining two values could be inferred from

and

. In other words,

there are only n −2 degrees of freedom available to the residuals r

given the

coeﬃcient estimates.

Example 2.4. In Example 2.3 using the gestation data, compute:

> df <- length(y) - 2

>s2<-RSS/df

> c( df = df, s=sqrt(s2), s2=s2 )

df s s2

19.0000000 0.7752701 0.6010438

2.3 Simple Linear Regression 39

The estimate of σ

is s

=0.6010. This information is automatically com-

puted by r when the lm() function is used (see Sect. 2.6). 

2.3.4 Standard Errors of the Coeﬃcients

The variances of the parameter estimates given in Sect. 2.3.2 (p. 36)are

var[

]=σ





¯x



and var[

where ¯x

is the weighted mean. An estimate of var[

], written var[

], is

found by substituting s

for the unknown true variance σ

The term standard error is commonly used in statistics to denote the

standard deviation of an estimated quantity. The standard errors of the co-

eﬃcients are the square roots of var[

se(

)=s





¯x



1/2

and se(

√

Example 2.5. For the gestation data model, the standard errors of the co-

eﬃcients are:

> var.b0 <- s2 * ( 1/sum(wts) + xbar^2 / SSx )

> var.b1 <- s2 / SSx

> sqrt( c( beta0=var.b0, beta1=var.b1) ) # The std errors

beta0 beta1

0.371172341 0.009493212

This information is automatically computed by r when the lm() function is

used (see Sect. 2.6). 

2.3.5 Standard Errors of Fitted Values

For a given value of the explanatory variable, say x

, the best estimate of the

mean response is the ﬁtted value ˆμ

. Since ˆμ

is a function of the

estimated parameters

and

, the estimate of μ

also contains uncertainty.

The variance of ˆμ

var[ ˆμ

]=σ





− ¯x)



40 2 Linear Regression Models

An estimate of var[ˆμ

], written var[ ˆμ

], is found by substituting s

for the

unknown true variance σ

. The standard error of ˆμ

, written se(ˆμ

), is the

square root of the variance.

Example 2.6. For the gestation data model, suppose we wish to use the

model to estimate the mean birthweight for a gestation length of 30 weeks:

> x.g <- 30

> mu.g <- beta0 + x.g * beta1

> var.mu.g <- s2 * ( 1/sum(wts) + (x.g-xbar)^2 / SSx )

> se.mu.g <- sqrt(var.mu.g)

> c( mu=mu.g, se=sqrt(var.mu.g))

mu se

1.934392 0.088124

The mean birthweight is estimated as ˆμ

=1.934 kg, with a standard error

of se(ˆμ

)=0.08812 kg. 

2.4 Estimation for Multiple Regression

2.4.1 Coeﬃcient Estimates

Now we return to the general situation, when there are p explanatory vari-

ables, and p



regression coeﬃcients β

to be estimated, for j =0, 1,...,p,

including the intercept. The regression model is given by Eq. (2.1).

As for simple linear regression, we deﬁne the sum of squared deviations

between the observations y

and the model means by

S =



i=1

− μ

)

For any given set of coeﬃcients β

, S measures how close the model means

are to the observed responses y

. Smaller values of S indicate that the μ

are closer to the y

, in general. The least-squares estimators of β

are deﬁned

to be those values of β

that minimize S, and are denoted

,...,

Using calculus, the minimum value of S occurs when

∂S

∂β

=0 forj =0, 1,...,p. (2.11)

The least-squares estimators are found by solving the set of p+1 simultaneous

equations (2.11). The solutions to these equations are best computed using

matrix algorithms, but the least-squares estimators can be well understood

and interpreted by writing them as:



i=1

∗



i=1

∗

)

, (2.12)

2.4 Estimation for Multiple Regression 41

for j =0,...,p, where x

∗

give the values for jth explanatory variable x

after being adjusted for the all other explanatory variables x

,...,x

apart

from x

. The adjusted explanatory variable x

∗

is that part of x

that cannot

be explained by regression on the other explanatory variables.

The ﬁtted values are

ˆμ



j=1

, (2.13)

and the residuals are the deviations of the responses from the ﬁtted values:

= y

− ˆμ

The values of the adjusted explanatory variable x

∗

are the residuals from the

linear regression of x

on the explanatory variables other than x

. Although

not immediately obvious, the formulae for the least-squares estimators (2.12)

are of the same form as that for the slope in simple linear regression (2.7).

In simple linear regression, the covariate x needs to be adjusted only for the

intercept term, so x

∗

=(x

− ¯x). Substituting this into (2.12) gives (2.7).

Note that σ

doesn’t appear in the least-squares equations. This means we

do not need to know the value of σ

in order to estimate the coeﬃcients β

Example 2.7. For the lung capacity data (lungcap), Fig. 2.4 shows that the

relationship between fev and height is not linear, so a linear model is not

appropriate. However, plotting the logarithm of fev against height does show

an approximate linear relationship (the function scatter.smooth() adds a

smooth curve to the plotted points):

45 50 55 60 65 70 75

FEV

Height (in inches)

FEV (in L)

45 50 55 60 65 70 75

−0.5

0.0

0.5

1.0

1.5

2.0

log of FEV

Height (in inches)

log of FEV (in L)

Fig. 2.4 fev plotted against height (left panel), and the logarithm of fev plotted

against height (right panel) for the lungcap data (Example 2.7)

42 2 Linear Regression Models

> scatter.smooth( lungcap$Ht, lungcap$FEV, las=1, col="grey",

ylim=c(0, 6), xlim=c(45, 75), # Use similar scales for comparisons

main="FEV", xlab="Height (in inches)", ylab="FEV (in L)" )

> scatter.smooth( lungcap$Ht, log(lungcap$FEV), las=1, col="grey",

ylim=c(-0.5, 2), xlim=c(45, 75), # Use similar scales for comparisons

main="log of FEV", xlab="Height (in inches)", ylab="log of FEV (in L)")

For the lungcap data then, ﬁtting a linear model for y = log(fev)may

be appropriate. On this basis, a possible linear regression model to ﬁt to the

data would be



var[y

]=σ

= β

+ β

(2.14)

where μ =E[y]fory = log(fev), x

is height, x

is age, x

is the dummy

variable (1.1) for gender (0 for females; 1 for males), and x

is the dummy

variable (1.2) for smoking (0 for non-smokers; 1 for smokers). Here, p



and n = 654. 

2.4.2 Estimating the Variance σ

The value of S evaluated at the least-squares estimates of β

is called the

residual sum-of-squares (rss):

rss =



i=1

− ˆμ

)

. (2.15)

The residual degrees of freedom associated with rss is equal to the number of

observations minus the number of regression coeﬃcients that were estimated

in evaluating rss, in this case n − p



. As for simple linear regression, an

unbiased estimator of σ

is obtained by dividing rss by the corresponding

degrees of freedom:



i=1

− ˆμ

)

n − p



rss

n − p



2.4.3 Standard Errors

Write I

∗



i=1



∗



for the sum of squares of the jth explanatory

variable adjusted for the other variables. This quantity I

∗

is a measure of

how well the regression model is leveraged to estimate the jth coeﬃcient. It

2.5 Matrix Formulation of Linear Regression Models 43

tends to be larger when x

is independent of the other explanatory variables

and smaller when x

is correlated with one or more of the other variables.

The variance of the jth coeﬃcient is

var[

]=σ

∗

An estimate of var[

], written var[

], is found by substituting s

for the

unknown true variance σ

. Then, the standard error becomes

se(

)=s/



∗

* 2.5 Matrix Formulation of Linear Regression Models

* 2.5.1 Matrix Notation

Using matrix algebra to describe data is convenient, and useful for simplifying

the mathematics. Denote the n×1 vector of responses as y, and the n×p



ma-

trix of explanatory variables, called the model matrix,asX=[x

, x

,...,x

where x

is the n×1 vector of values for x

. We write x

for the vector of ones

(the constant term) for convenience. The linear regression model in matrix

form is



var[y]=W

−1

μ =Xβ,

(2.16)

where E[y]=μ, and W

−1

is a known, positive-deﬁnite symmetric matrix of

size n × n. A special case occurs when the diagonal elements (i, i)ofW

−1

are 1/w

and the oﬀ-diagonal elements are zero, equivalent to (2.1). Most

commonly, observations are weighted identically, so that W

−1

, where I

is an n × n identity matrix.

Example 2.8. For the gestation data in Example 2.1 (p. 32), n =21andso

y is a 21 × 1 vector, and X is a 21 × 2 model matrix (that is, p



= 2). The

vector y , matrix X, and covariance matrix W

−1

are

y =

⎡

⎢

⎣

0.520

0.700

1.000

3.612

3.390

3.740

⎤

⎥

⎦

;X=

⎡

⎢

⎣

122

123

125

142

143

144

⎤

⎥

⎦

−1

⎡

⎢

⎣

1/10 0... 000

01/10... 000

001/1 ... 000

000... 1/53 0 0

000... 01/90

000... 001/1

⎤

⎥

⎦

The columns of X are the vector of ones and the gestational ages. 

44 2 Linear Regression Models

Example 2.9. To write the model proposed for the lungcap data in

Example 2.7, ﬁrst recall that p



=5andn = 654. Then, the 654 × 1

vector y = log(fev), the 654 ×5 model matrix X, and the 5 ×1 vector β are

y =

⎡

⎢

⎣

0.0695

−0.176

0.0971

1.48

⎤

⎥

⎦

;X=

⎡

⎢

⎣

134600

144800

11870.511

⎤

⎥

⎦

; β =

⎡

⎢

⎣

⎤

⎥

⎦

where the columns of X are the constant term (always one), Age, Ht,the

dummy variable for Gender, and the dummy variable for Smoke. The weight

matrix W is the 654×654 identity matrix I

654

. Model (2.14) written in matrix

notation is then



var[y]=I

654

μ =Xβ,

where E[y] = E[log(fev)] = μ. 

* 2.5.2 Coeﬃcient Estimates

The simultaneous solutions to the least-squares equations (2.11) are most

conveniently found using matrix algebra. Using matrix notation, write the

weighted sum-of-squared deviations (Sect. 2.4.1)as

S =(y − μ)

W(y − μ), (2.17)

where μ =Xβ. Diﬀerentiating S with respect to β and setting to zero shows

that the minimum value of S (the rss) occurs when

WXβ =X

Wy (2.18)

(Problem 2.4). The matrix X

WX must be invertible for this equation to

have a unique solution, and so X must be of full column-rank. The solution

can be written as

β =(X

WX)

−1

Wy. (2.19)

Using matrix algebra, it is straightforward to show that

β is an unbiased

estimator of β (Problem 2.6). Then the ﬁtted values are

μ =X

β.

Although not immediately obvious, the matrix formula for

β (2.19)has

essentially the same form as the non-matrix expressions (2.7) and (2.12). In

each case, the formula for

β consists of a sum of cross-products of x and y

(here X

Wy) divided by a sum of squares of x values (here X

WX). The

2.5 Matrix Formulation of Linear Regression Models 45

expressions (2.12) and (2.19) are equivalent, although the matrix version is

more appropriate for computation.

Numerically eﬃcient algorithms do not implement Eq. (2.19) by inverting

WX explicitly. A more eﬃcient approach is to obtain

β directly as the

solution to the linear system of Eqs. (2.18). The default numerical algorithms

used by the built-in regression functions in r are even more sophisticated, and

avoid computing X

WX altogether. This is done via the QR-decomposition

of X, such that XW

1/2

= QR where Q satisﬁes Q

Q = I and R is an upper-

triangular matrix. Details of these computations are beyond the scope of this

book. Rather, it will be suﬃcient to know that r implements eﬃcient and

stable numerical algorithms for computing

β and other regression output.

Example 2.10. Consider ﬁtting the linear regression model (2.14) to the lung

capacity data. Observations are not weighted and hence W

−1

,souser

as follows:

> data(lungcap)

> lungcap$Smoke <- factor(lungcap$Smoke, levels=c(0, 1),

labels=c("Non-smoker","Smoker"))

> Xmat <- model.matrix( ~ Age + Ht + factor(Gender) + factor(Smoke),

data=lungcap)

Here, model.matrix() is used to combine the variables as columns of a ma-

trix, after declaring Smoke as a factor.

> head(Xmat)

(Intercept) Age Ht factor(Gender)M factor(Smoke)Smoker

11346 0 0

21448 0 0

31448 0 0

41448 0 0

51449 0 0

61449 0 0

> XtX <- t(Xmat) %*% Xmat # t() is transpose; %*% is matrix multiply

> y <- log(lungcap$FEV)

> inv.XtX <- solve( XtX ) # solve returns the matrix inverse

> XtY <- t(Xmat) %*% y

> beta <- inv.XtX %*% XtY; drop(beta)

(Intercept) Age Ht

-1.94399818 0.02338721 0.04279579

factor(Gender)M factor(Smoke)Smoker

0.02931936 -0.04606754

(drop() drops any unnecessary dimensions. In this case it reduces a single-

column matrix to a vector.) The ﬁtted model has the systematic component

ˆμ = −1.944 + 0.02339Age +0.04280Ht +0.02932Gender − 0.04607Smoke,

46 2 Linear Regression Models

where Gender is 0 for females and 1 for males, and Smoke is 0 for non-smokers

and 1 for smokers. Slightly more eﬃcient code would have been to compute

β by solving a linear system of equations:

> beta <- solve(XtX, XtY); beta

[,1]

(Intercept) -1.94399818

Age 0.02338721

Ht 0.04279579

factor(Gender)M 0.02931936

factor(Smoke)Smoker -0.04606754

giving the same result. An even more eﬃcient approach would have been to

use the QR-decomposition:

> QR <- qr(Xmat)

> beta <- qr.coef(QR, y); beta

(Intercept) Age Ht

-1.94399818 0.02338721 0.04279579

factor(Gender)M factor(Smoke)Smoker

0.02931936 -0.04606754

again giving the same result. 

* 2.5.3 Estimating the Variance σ

After computing

β, the ﬁtted values are obtained as

μ =X

β. The variance

is estimated from the rss as usual:

(y −

μ)

W(y −

μ)

n − p



rss

n − p



Example 2.11. In Example 2.10, for the model relating log(fev) to age,

height, gender and smoking status for the lungcap data, compute:

> mu <- Xmat %*% beta

> RSS <- sum( (y - mu)^2 ); RSS

[1] 13.73356

> s2 <- RSS / ( length(lungcap$FEV) - length(beta) )

> c(s=sqrt(s2), s2=s2)

ss2

0.14546857 0.02116111

The estimate of σ

is s

=0.02116. Of course, these calculations are per-

formed automatically by lm(). 

2.5 Matrix Formulation of Linear Regression Models 47

* 2.5.4 Estimating the Variance of

Using (2.19), the covariance matrix for

β is (Problem 2.7)

var[

β]=σ

WX)

−1

. (2.20)

The diagonal elements of var[

β] are the values of var[

]. An estimate of this

covariance matrix is found by using s

as an estimate of σ

var[

β]=s

WX)

−1

. (2.21)

The diagonal elements of var[

β] are the values of var[

], from which the es-

timated standard errors of the individual parameters are computed: se(



var[

Example 2.12. For the model relating fev to age, height, gender and smoking

status, as used in Examples 2.10 and 2.11 (data set: lungcap):

> var.matrix <- s2 * inv.XtX

> var.betaj <- diag( var.matrix ) # diag() grabs the diagonal elements

> sqrt( var.betaj )

(Intercept) Age Ht

0.078638583 0.003348451 0.001678968

factor(Gender)M factor(Smoke)Smoker

0.011718565 0.020910198

Hence, se(

)=0.07864 and se(

)=0.003348, for example. Of course, these

calculations are performed automatically by lm(). 

* 2.5.5 Estimating the Variance of Fitted Values

For known values of the explanatory variables, given in the row vector x

of length p



say, the best estimate of the mean response is the ﬁtted value

ˆμ

= x

β. Since ˆμ

is a function of the estimated parameters

β, the estimate

of μ

also contains uncertainty. The variance of ˆμ

var[ ˆμ

]=var[x

β]=x

WX)

−1

An estimate of var[ˆμ

], written var[ ˆμ

], is found by substituting s

for the

unknown true variance σ

. The standard error is then

se(ˆμ

)=s



WX)

−1

Example 2.13. For the lungcap data, Example 1.6 suggested a linear relation-

ship between log(fev) and height. Suppose we wish to estimate the mean of

48 2 Linear Regression Models

log(fev) for females (that is, x

= 0) that smoke (that is, x

= 1), aged 18

who are 66 inches tall using the model in (2.14):

> xg.vec <- matrix( c(1, 18, 66, 0, 1), nrow=1)

> ### The first "1" is the constant term

> mu.g <- xg.vec %*% beta

> var.mu.g <- sqrt( xg.vec %*% (solve(t(Xmat)%*%Xmat)) %*% t(xg.vec) * s2)

> c( mu.g, var.mu.g )

[1] 1.25542621 0.02350644

The estimate of log(fev)isˆμ

=1.255 L, with a standard error of se(ˆμ

√

0.02351 = 0.1533 L. 

2.6 Fitting Linear Regression Models Using R

Performing explicit computations in r to estimate unknown model param-

eters, as demonstrated in Sects. 2.3 and 2.5, is tedious and unnecessary. In

r, linear regression models are conveniently ﬁtted to data using the function

lm(). Basic use of the lm() function requires specifying the response and

explanatory variables.

Example 2.14. Fitting the regression model (2.2) for the birthweight data

frame gestation (Example 2.1,p.32) requires the prior weights (the number

of birth, Births) to be explicitly supplied in addition to the response and

explanatory variable:

> gest.wtd <- lm( Weight ~ Age, data=gestation,

weights=Births) # The prior weights

> summary(gest.wtd)

Call:

lm(formula = Weight ~ Age, data = gestation, weights = Births)

Weighted Residuals:

Min 1Q Median 3Q Max

-1.62979 -0.60893 -0.30063 -0.08845 1.03880

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) -2.678389 0.371172 -7.216 7.49e-07 ***

Age 0.153759 0.009493 16.197 1.42e-12 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Residual standard error: 0.7753 on 19 degrees of freedom

Multiple R-squared: 0.9325, Adjusted R-squared: 0.9289

F-statistic: 262.3 on 1 and 19 DF, p-value: 1.416e-12

The ﬁrst argument to the lm() function is a model formula: Weight ~ Age.

The symbol ~ is read as ‘is modelled by’. The response variable (in this case

2.6 Fitting Linear Regression Models Using R 49

Weight) is placed on the left of the ~, and the explanatory variables are placed

on the right of the ~ and are joined by + signs if there are more than one.

The second argument data=gestation indicates the data frame in which the

variables are located. The argument weights speciﬁes the prior weights w

and can be omitted if all the prior weights are equal to one.

We can also ﬁt the regression without using prior weights for comparison:

> gest.ord <- lm( Weight ~ Age, data=gestation); coef(gest.ord)

(Intercept) Age

-3.049879 0.159483

Using the prior weights (Fig. 2.5, solid line), the regression line is closer

to the observations weighted more heavily (which contain more information)

than the ordinary regression line (dashed line):

> plot( Weight ~ Age, data=gestation, type="n",

las=1, xlim=c(20, 45), ylim=c(0, 4),

xlab="Gestational age (weeks)", ylab="Mean birthweight (in kg)" )

> points( Weight[Births< 20] ~ Age[Births< 20], pch=1, data=gestation )

> points( Weight[Births>=20] ~ Age[Births>=20], pch=19, data=gestation )

> abline( coef(gest.ord), lty=2, lwd=2)

> abline( coef(gest.wtd), lty=1, lwd=2)

> legend("topleft", lwd=c(2, 2), bty="n",

lty=c(2, 1, NA, NA), pch=c(NA, NA, 1, 19), # NA shows nothing

legend=c("Ordinary regression", "Weighted regression",

"Based on 20 or fewer obs.","Based on more than 20 obs."))

20 25 30 35 40 45

Gestational age (weeks)

Mean birthweight (in kg)

Ordinary regression

Weighted regression

Based on 20 or fewer obs.

Based on more than 20 obs.

Fig. 2.5 A plot of birthweights against gestational age from Table 2.1. The ﬁlled dots

are used for the means based on more than 20 observations, and hollow dots for other

observations. The solid line is the ordinary regression line, while the dashed line is

weighted regression line (Example 2.1)

50 2 Linear Regression Models

The systematic components are drawn using abline(), which needs the in-

tercept and the slope to draw the straight lines (which are both returned

using coef()). 

Example 2.15. Consider ﬁtting the Model (2.14) to the lung capacity data

(lungcap), using age, height, gender and smoking status as explanatory vari-

ables, and log(fev) as the response:

> # Recall, Smoke has been declared previously as a factor

> lm( log(FEV) ~ Age + Ht + Gender + Smoke, data=lungcap )

Call:

lm(formula = log(FEV) ~ Age + Ht + Gender + Smoke, data = lungcap)

Coefficients:

(Intercept) Age Ht GenderM SmokeSmoker

-1.94400 0.02339 0.04280 0.02932 -0.04607

The output of the lm() command as shown above is brief, and shows that

the estimated systematic component is

ˆμ = −1.944 + 0.02339x

+0.04280x

+0.02932x

− 0.04607x

(2.22)

where μ = E[log fev], for Age x

and Ht x

. Gender is a factor, but does not

need to be explicitly declared as a factor (using factor()) since the variable

Gender is non-numerical (Sect. 1.4). The default coding used in r sets x

for females F and x

= 1 for males M,asin(1.1)(p.10). The M following the

name of the variable Gender in the r output indicates that Gender is 1 for

males (see Sect. 1.4). Smoke is a factor, but must be explicitly declared as a

factor (using factor()).

The constant term in the model is included implicitly by r, since it is

almost always necessary. To explicitly exclude the constant in the model

(which is unusual), use one of these forms:

> lm( log(FEV)~0+Age+Ht+Gender + Smoke, data=lungcap)#Noconst.

> lm( log(FEV) ~ Age + Ht + Gender + Smoke - 1, data=lungcap)#Noconst.

r returns more information about the ﬁtted model by directing the output

of lm() to an output object:

> LC.m1 <- lm( log(FEV) ~ Age + Ht + Gender + Smoke, data=lungcap )

The output object LC.m1 contains a great deal of information about the ﬁtted

model:

> names( LC.m1 ) # The names of the components of LC.m1

[1] "coefficients" "residuals" "effects" "rank"

[5] "fitted.values" "assign" "qr" "df.residual"

[9] "contrasts" "xlevels" "call" "terms"

[13] "model"

2.6 Fitting Linear Regression Models Using R 51

Fig. 2.6 The output of the summary() command after using lm() for the lungcap data

Each of these components can be accessed directly using constructs like, for

example, LC.m1$coefficients. However, most of the useful information is

accessed using r functions, such as coef(LC.m1), as demonstrated below.

These functions are discussed throughout this chapter, and are summarized

in Sect. 2.14. A summary of the information contained in the LC.m1 object

is displayed using the summary() command (Fig. 2.6). Most of this output is

explained in later sections, which refer back to the output in Fig. 2.6.

For now, observe that the parameter estimates are shown in the table in the

middle of the output (starting from line 14), in the column labelled Estimate.

The estimated standard errors appear in the column labelled Std. Error.

The parameter estimates are explicitly obtained using:

> coef( LC.m1 )

(Intercept) Age Ht GenderM SmokeSmoker

-1.94399818 0.02338721 0.04279579 0.02931936 -0.04606754

The estimate of σ is:

> summary( LC.m1 )$sigma

[1] 0.1454686

This information (as well as the residual degrees of freedom) appears in line 24

of the output shown in Fig. 2.6. 

52 2 Linear Regression Models

2.7 Interpreting the Regression Coeﬃcients

After ﬁtting a model, interpretation of the model is strongly encouraged to

determine if the model makes physical sense, and to understand the story the

model is telling (Sect. 1.7).

The systematic component of linear regression model ﬁtted to the gestation

data (Example 2.14)is

ˆμ = −2.678 + 0.1538x,

where μ =E[y], where y is the mean birthweight (in kg), and x is the gesta-

tional age in weeks. This model indicates that the mean birthweight increases

by approximately 0.1538 kg for each extra week of gestation, on average, over

the range of the data. The random component implies that the variation of

the weights around μ is approximately constant with s

=0.6010.

The interpretation for the systematic component model ﬁtted to the lung

capacity data (Example 2.15) is diﬀerent, because the response variable is

log(fev). This means that the systematic component is

μ = E[log(fev)]

= −1.944 + 0.02339x

+0.04280x

+0.02932x

− 0.04607x

(2.23)

for Age x

, Ht x

, the dummy variable for Gender x

and the dummy vari-

able for Smoke x

. The regression coeﬃcients can only be interpreted for

their impact on μ = E[log(fev)] and not on E[fev] directly. However, since

E[log y] ≈ log E[y] = log μ (Problem 2.11), then (2.23) can be written as

log μ = log E[fev]

≈−1.944 + 0.02339x

+0.04280x

+0.02932x

− 0.04607x

. (2.24)

Now the parameter estimates can be used to approximately interpret the

eﬀects of the explanatory variables on μ =E[fev] directly. For example, an

increase in height x

of one inch is associated with an increase in the mean

fev by a factor of exp(0.04280) = 1.044, assuming all other variables are

kept constant.

Parameter estimates for qualitative explanatory variables indicate how

much the value of μ changes compared to the reference level (after adjusting

for the eﬀect of other variables), provided treatment coding is used (Sect. 1.4).

For the systematic component in (2.24), the value of μ will change by a factor

of exp(−0.04607) = 0.9550 for smokers (Smoke=1) compared to non-smokers

(Smoke=0). In other words, fev is likely to be a factor of 0.9550 lower for

smokers, assuming all other variables are kept constant.

The random component of the model (Example 2.15) indicates the vari-

ation of log(fev) around μ = E[log(fev)] is approximately constant, with

=0.02116.

2.8 Inference for Linear Regression Models: t-Tests 53

Interpreting the eﬀects of correlated covariates is subtle. For example, in

the lung capacity data, height and age are positively correlated (Sect. 1.7).

Height generally increases with age for youth, so the eﬀect on fev of increas-

ing age for ﬁxed height is not the same as the overall increase in fev as age

increases. The overall increase in fev would reﬂect the combined eﬀects of

height and age as both increase. The coeﬃcient in the linear model reﬂects

only the net eﬀect of a covariate, eliminating any concomitant changes in the

other covariates that might normally be present if all the covariate varied in

an uncontrolled fashion.

Also, note that the data are observational, so no cause-and-eﬀect conclu-

sion is implied (Sect. 1.7).

2.8 Inference for Linear Regression Models: t-Tests

2.8.1 Normal Linear Regression Models

Up to now, no speciﬁc statistical distribution has been assumed for the re-

sponses in the regression. The responses have simply been assumed to be

independent and to have constant variance. However, to undertake formal

statistical inference we need to be more speciﬁc. The usual assumption of lin-

ear regression is that the responses are normally distributed, either with con-

stant variance or with variances that are proportional to the known weights.

This can be stated as:

⎧

⎪

⎨

⎪

⎩

∼ N(μ

,σ

)

= β



j=1

(2.25)

Model (2.25) is called a normal linear regression model. Under the assump-

tions of this model, hypothesis tests and conﬁdence intervals can be devel-

oped. In practice, the assumption of normality is not as crucial is it might

appear, as most of the tests we will develop remain valid for large n even

when the responses are not normally distributed. The main signiﬁcance of

the normality therefore is to develop tests and conﬁdence intervals that are

valid for small sample sizes.

2.8.2 The Distribution of

Expressions for computing estimates of var[

] were given in Sects. 2.3.4

and 2.5.4. When a normal linear regression model (2.25) is adopted, the entire

distributions of the regression parameters are known, not just the variance.

Using Model (2.25), the

are random variables which follow normal distri-

54 2 Linear Regression Models

butions, since

is a linear combination of the y

(Sect. 2.5.2). Speciﬁcally,

for normal linear regression models,

∼ N(β

, var[

]). (2.26)

This means that

has a normal distribution with mean β

and variance

var[

]. Note that var[

] is a product of σ (approximately inversely propor-

tional to

√

n ) and the known values of the explanatory variable and weights.

From (2.26),

Z =

− β

se(

)

where se(



var[

], and Z has a standard normal distribution when σ

is known. When σ

is unknown, estimate σ

by s

and hence estimate var[

]

by var[

]. Then

T =

− β

se(

)

has a Student’s t distribution with n −p



degrees of freedom, where se(



var[

]. Note that Student’s t-distribution converges to the standard nor-

mal as the degrees of freedom increase.

2.8.3 Hypothesis Tests for β

Consider testing the null hypothesis H

: β

= β

against a one-sided alterna-

tive (H

: β

>β

or H

: β

<β

) or a two-sided alternative (H

: β

= β

where β

is some hypothesized value of β

(usually zero). The statistic

T =

− β

se(

)

(2.27)

is used to test this hypothesis. When H

is true, T has a t-distribution with

n − p



degrees of freedom when σ

is unknown, so we determine signiﬁcance

by referring to this distribution.

Each individual t-test determines whether evidence exists that the param-

eter is statistically signiﬁcantly diﬀerent from β

in the presence of the other

variables currently in the model.

Example 2.16. After ﬁtting Model (2.22) to the lung capacity data in r (data

set: lungcap), the output of the summary() command in Fig. 2.6 (p. 51)

reports information about the parameter estimates in the table in the centre

of the output (starting from line 14):

2.8 Inference for Linear Regression Models: t-Tests 55

•theEstimate column contains the parameter estimates

;

•the Std. Error column contains the corresponding standard errors

se(

);

•thet value column contains the corresponding t-statistic (2.27) for test-

ing H

: β

=0;

•thePr(>|t|) column contains the corresponding two-tailed P -values for

the hypothesis tests. (The one-tailed P -value is the two-tailed P -value

divided by two.)

Line 22 in Fig. 2.6 (p. 51) regarding Signif. codes needs explanation. The

*** indicates a two-tailed P-value between 0 and 0.001; ** indicates a two-

tailed P -value between 0.001 and 0.01; * indicates a two-tailed P -value be-

tween 0.01 and 0.05; . indicates a two-tailed P-value between 0.05 and 0.10.

This information can be accessed directly using coef(summary()):

> round(coef( summary( LC.m1 ) ), 5)

Estimate Std. Error t value Pr(>|t|)

(Intercept) -1.94400 0.07864 -24.72067 0.00000

Age 0.02339 0.00335 6.98449 0.00000

Ht 0.04280 0.00168 25.48933 0.00000

GenderM 0.02932 0.01172 2.50196 0.01260

SmokeSmoker -0.04607 0.02091 -2.20311 0.02794

For example, consider a hypothesis test for β

(the coeﬃcient for Smoke). To

test H

: β

= 0 against the alternative H

: β

= 0 (in the presence of age,

height and gender), the output shows that the t-score is t = −2.203, and

the corresponding two-tailed P -value is 0.02794. Thus, some evidence exists

that smoking status is statistically signiﬁcant when age, height and gender

are in the model. If gender was omitted from the model and the relevant

null hypothesis retested, the test has a diﬀerent meaning: this second test

determines if age is signiﬁcant in the model adjusted only for height (but not

gender). Consequently, we should expect the test statistic and P -values to be

diﬀerent, and so the conclusion may diﬀer also. 

2.8.4 Conﬁdence Intervals for β

While hypothesis tests are useful for detecting statistical signiﬁcance, often

the size of the eﬀect is of greater interest. This can be estimated by computing

conﬁdence intervals. The estimates

and the corresponding standard errors

se(

) can be used to form 100(1−α)% conﬁdence intervals for each estimate

using

± t

∗

α/2,n−p



se(

where t

∗

α/2,n−p



is the value such that an area α/2 is in each tail of the t-

distribution with n −p



degrees of freedom. Rather than explicitly using the

56 2 Linear Regression Models

formula, conﬁdence intervals are found in r using the confint() command.

By default, 95% conﬁdence intervals are produced; other levels are produced

by using, for example, level=0.90 in the call to confint().

Example 2.17. For the lung capacity data (data set: lungcap), ﬁnd the 95%

conﬁdence interval for all ﬁve regression coeﬃcients in model LC.m1 using

confint():

> confint( LC.m1 )

2.5 % 97.5 %

(Intercept) -2.098414941 -1.789581413

Age 0.016812109 0.029962319

Ht 0.039498923 0.046092655

GenderM 0.006308481 0.052330236

SmokeSmoker -0.087127344 -0.005007728

For example, the 95% conﬁdence interval for β

is from −0.08713 to

−0.005008. 

2.8.5 Conﬁdence Intervals for μ

The ﬁtted values ˆμ are used to estimate the mean value for given values

of the explanatory variables. Using the expressions for computing var[ˆμ

]

(Sect. 2.3.5; Sect. 2.5.5), the 100(1 − α)% conﬁdence interval for the ﬁtted

value is

ˆμ

± t

∗

α/2,n−p



se(ˆμ),

where se(ˆμ



var[ ˆμ

], and where t

∗

α/2,n−p



is the value such that an area

α/2 is in each tail of the t-distribution with n−p



degrees of freedom. Rather

than explicitly using the formulae, r returns the standard errors when making

predictions using predict() with the input se.fit=TRUE, from which the

conﬁdence intervals can be formed.

Example 2.18. For the lung capacity data (data set: lungcap), suppose we

wish to estimate μ = E[log(fev)] for female smokers aged 18 who are 66

inches tall. Using r, we ﬁrst create a new data frame containing the values

of the explanatory variables for which we need to make the prediction:

> new.df <- data.frame(Age=18, Ht=66, Gender="F", Smoke="Smoker")

Then, use predict() to compute the estimates of μ:

> out <- predict( LC.m1, newdata=new.df, se.fit=TRUE)

> names(out)

[1] "fit" "se.fit" "df" "residual.scale"

> out$se.fit

[1] 0.02350644

2.8 Inference for Linear Regression Models: t-Tests 57

> tstar <- qt(df=LC.m1$df, p=0.975 ) # For a 95% CI

> ci.lo <- out$fit - tstar*out$se.fit

> ci.hi <- out$fit + tstar*out$se.fit

> CIinfo <- cbind( Lower=ci.lo, Estimate=out$fit, Upper=ci.hi)

> CIinfo

Lower Estimate Upper

1 1.209268 1.255426 1.301584

The prediction is ˆμ =1.255, and the 95% conﬁdence interval is from 1.209 to

1.302. Based on the discussion in Sect. 2.7, an approximate conﬁdence interval

for E[fev]is

> exp(CIinfo)

Lower Estimate Upper

1 3.351032 3.509334 3.675114

This idea can be extended to compute the conﬁdence intervals for 18 year-

old female smokers for varying heights:

> newHt <- seq(min(lungcap$Ht), max(lungcap$Ht), by=2)

> newlogFEV <- predict( LC.m1, se.fit=TRUE,

newdata=data.frame(Age=18, Ht=newHt, Gender="F", Smoke="Smoker"))

> ci.lo <- exp( newlogFEV$fit - tstar*newlogFEV$se.fit )

> ci.hi <- exp( newlogFEV$fit + tstar*newlogFEV$se.fit )

Notice that the intervals do not have the same width over the whole range

of the data:

> cbind( Ht=newHt, FEVhat=exp(newlogFEV$fit), SE=newlogFEV$se.fit,

Lower=ci.lo, Upper=ci.hi, CI.Width=ci.hi - ci.lo)

Ht FEVhat SE Lower Upper CI.Width

1 46 1.491095 0.04886534 1.354669 1.641259 0.2865900

2 48 1.624341 0.04585644 1.484469 1.777392 0.2929226

3 50 1.769494 0.04289937 1.626540 1.925011 0.2984711

4 52 1.927618 0.04000563 1.781987 2.085151 0.3031639

5 54 2.099873 0.03719000 1.951990 2.258959 0.3069685

6 56 2.287520 0.03447163 2.137804 2.447722 0.3099183

7 58 2.491936 0.03187542 2.340743 2.652894 0.3121513

8 60 2.714619 0.02943370 2.562170 2.876138 0.3139672

9 62 2.957201 0.02718813 2.803464 3.119368 0.3159041

10 64 3.221460 0.02519123 3.065984 3.384820 0.3188364

11 66 3.509334 0.02350644 3.351032 3.675114 0.3240817

12 68 3.822932 0.02220493 3.659826 3.993308 0.3334820

13 70 4.164555 0.02135689 3.993518 4.342917 0.3493998

14 72 4.536705 0.02101728 4.353286 4.727852 0.3745665

15 74 4.942111 0.02121053 4.740502 5.152294 0.4117924



58 2 Linear Regression Models

2.9 Analysis of Variance for Regression Models

A linear regression model, having been ﬁtted to the data by least squares,

yields a ﬁtted value

ˆμ



j=1

for each observation y

. Each observation therefore can be separated into a

component predicted by the model, and the remainder or residual that is left

over, as

=ˆμ

+(y

− ˆμ

In other words, Data = Fit + Residual.

The simplest possible regression model is that with p = 0 and no covari-

ates x

.Inthatcaseˆμ =

=¯y

, where ¯y



i=1



i=1

is the

weighted mean of the observations. In order to evaluate the contribution of

the covariates x

, it is more useful to consider the corresponding decompo-

sition of the mean-corrected data,

− ¯y

=(ˆμ

− ¯y

)+(y

− ˆμ

Squaring each of these terms and summing them over i leads to the key

identity

sst = ssReg + rss

where sst =



i=1

− ¯y

)

is the total sum of squares, ssReg =



i=1

(ˆμ

− ¯y

)

is the regression sum of squares,andrss =



i=1

−

ˆμ

)

is the residual sum of squares. The cross-product terms (ˆμ

−¯y

)(y

−ˆμ

)

sum to zero, and so don’t appear in this identity. The identity embodies the

principle that variation in the response variable comes from two sources:

ﬁrstly a systematic component that can be attributed to changes in the ex-

planatory variables (ssReg), and secondly a random component that cannot

be predicted (rss). This identity is the basis of what is called analysis of

variance, because it analyses the sources from which variance in the data

arises.

It is of key interest to know whether the explanatory variables are useful

predictors of the responses. This question can be answered statistically by

testing whether the regression sum of squares ssReg is larger than would be

expected due to random variation; in other words, whether ssReg is large

relative to rss after taking the number of explanatory variables into account.

The null hypothesis is the assertion that β

= 0 for all j =1,...,p.To

develop such a test, ﬁrst note that rss/σ

has a chi-square distribution with

n − p



degrees of freedom, for a normal linear regression model. Likewise,

under the null hypothesis, it can be shown that ssReg/σ

has a chi-square

2.9 Analysis of Variance for Regression Models 59

Tabl e 2 .2 The general form of an analysis of variance table for a linear regression model

(Sect. 2.9)

Source of variation Sums of squares df Mean square F

Systematic component ssReg p



− 1 msReg =

ssReg



− 1

F =

msReg

mse

Random component rss n − p



mse =

rss

n − p



= s

Total variation sst n − 1

distribution with p



− 1 degrees of freedom for a normal linear regression

model. This means that the ratio

F =

ssReg/(p



− 1)

rss/(n − p



)

msReg

mse

(2.28)

follows an F -distribution with (p



− 1,n− p



) degrees of freedom. The mse,

the mean-square error, is equal to s

, the unbiased estimator of σ

that we

have previously seen. msReg is the mean-square for the regression.

A large value for F means that the proportion of the variation that can be

explained by the systematic component is large relative to s

; a small value

for F means that the proportion of the variation that can be explained by

the systematic component is small relative to s

The computations are conveniently arranged in an analysis of variance

(anova) table (Table 2.2).

The r summary() command does not show the details of the anova ta-

ble (Fig. 2.6,p.51), but the results are reported in the ﬁnal line of output

(line 26): the F -statistic is labelled F-statistic, followed by the correspond-

ing degrees of freedom (labelled DF), and the P -value for the test (labelled

p-value). The F -statistic and the corresponding degrees of freedom are re-

turned using summary(LC.m1)$fstatistic. There is also an anova() func-

tion that is demonstrated in the next section.

The proportion of the total variation explained by the regression is the

coeﬃcient of determination,

ssReg

sst

=1−

rss

sst

. (2.29)

Clearly, by the deﬁnition, R

is bounded between zero and one. R

is some-

times also called multiple R

, because it is equal to the squared Pearson cor-

relation coeﬃcient between the y

and the ﬁtted values ˆμ

, using the weights

. r reports the value of R

in the model summary(), as shown in Fig. 2.6

(p. 51), where R

is labelled Multiple R-squared on line 25.

60 2 Linear Regression Models

Adding a new explanatory variable to the regression model cannot increase

rss and hence R

tends to increase with the size p of the model even if the

explanatory variables have no real explanatory power. For this reason, some

statisticians like to adjust R

for the number of explanatory variables in the

model. The adjusted R

, denoted

, is deﬁned by

=1−

rss/(n − p



)

sst/(n − 1)

=1− (1 −R

)

n − 1

n − p



It can be seen that 1 −

is the ratio of the residual to the total in the mean

square column of the anova table, whereas 1 −R

is the corresponding ratio

for the sums of squares column. However

is not the ratio of msReg to

sst/(n − 1), because the entries is the mean square column do not sum.

Unlike R

may be negative. This occurs whenever msReg < mse,which

can be taken to indicate a very poor model. In the model summary() (Fig. 2.6,

p. 51), r reports

, called Adjusted R-squared. F and R

are closely

related quantities (Problem 2.8), but it is F that is used to formally test

whether the regression is statistically signiﬁcant.

Example 2.19. For the lung capacity data (data set: lungcap), and

Model (2.22) with age, height, gender and smoking status as explanatory

variables, compute rss and sst (recalling that y = log(FEV)):

> mu <- fitted( LC.m1 ); RSS <- sum( (y - mu)^2 )

> SST <- sum( (y - mean(y) )^2 )

> c(RSS=RSS, SST=SST, SSReg = SST-RSS)

RSS SST SSReg

13.73356 72.52591 58.79236

> R2 <- 1 - RSS/SST # Compute R2 explicitly

> c( "Output R2" = summary(LC.m1)$r.squared, "Computed R2" = R2,

"adj R2" = summary(LC.m1)$adj.r.squared)

Output R2 Computed R2 adj R2

0.8106393 0.8106393 0.8094722

The analysis of variance table (Table 2.3) compiles the necessary information.

Compare these results to the output of summary(LC.m1) in Fig. 2.6 (p. 51).

The summary of the F -test, which includes the numerator and denominator

degree of freedom, is

> summary(LC.m1)$fstatistic

value numdf dendf

694.5804 4.0000 649.0000



2.10 Comparing Nested Models 61

Tabl e 2 .3 The anova table for Model (2.22) ﬁtted to the lung capacity data, parti-

tioning the total sum-of-squares into components due to the systematic and random

components (Example 2.19)

Source ss df ms F

Systematic component 58.79 4 14.70 694.6

Random component 13.73 649 0.02116

Total variation 72.53 653

2.10 Comparing Nested Models

2.10.1 Analysis of Variance to Compare Two Nested

Models

Rather than evaluating a single model, a researcher may wish to compare

two models. First consider comparing two nested linear regression models.

Model A is nested in Model B if Model A can be obtained from Model B by

setting some parameter(s) in Model B to zero or, more generally, if Model A is

a special case of Model B. For example, for the lung capacity data a researcher

may wish to compare two models with the systematic components

Model A: μ

= β

+ β

;

Model B: μ

= β

+ β

Model A is nested in Model B, since Model A is a special case of Model B

obtained by setting β

= β

=0.

In comparing these models, we wish to know whether the more complex

Model B is necessary, or whether the simpler Model A will suﬃce. Formally,

the null hypothesis is that the two models are equivalent, so that we test H

= β

= 0 against the alternative that β

and β

are not both zero.

Consider using the lungcap data frame, and ﬁtting the two models:

> LC.A <- lm( log(FEV) ~ Age + Smoke, data=lungcap )

> LC.B <- lm( log(FEV) ~ Age + Ht + Gender + Smoke, data=lungcap )

Now compute the respective rss:

> RSS.A <- sum( resid(LC.A)^2 ) # resid() computes residuals

> RSS.B <- sum( resid(LC.B)^2 )

> c( ModelA=RSS.A, ModelB=RSS.B)

ModelA ModelB

28.91982 13.73356

62 2 Linear Regression Models

The diﬀerence between the values of rss is called the sum-of-squares (or ss):

> SS <- RSS.A - RSS.B; SS

[1] 15.18626

> DF <- df.residual(LC.A) - df.residual(LC.B); DF

[1] 2

The ss measures the reduction in the rss gained by using the more complex

Model B. This reduction in rss is associated with an increase of two degrees

of freedom. Is this reduction statistically signiﬁcant?

The formal test requires comparing the ss divided by the change in the

degrees of freedom, to the rss for Model B divided by the degrees of freedom

for Model B:

> df.B <- df.residual(LC.B); df.B

[1] 649

> Fstat <- (SS/DF) / ( RSS.B/df.B ); Fstat

[1] 358.8249

A P -value is found by comparing to an F -distribution with (2, 649) degrees

of freedom:

> pf(Fstat, df1=DF, df2=df.B, lower.tail=FALSE)

[1] 1.128849e-105

The P -value is almost zero, providing strong evidence that Model B is signif-

icantly diﬀerent from Model A. In r, the results are displayed using anova():

> anova( LC.A, LC.B )

Analysis of Variance Table

Model 1: log(FEV) ~ Age + Smoke

Model 2: log(FEV) ~ Age + Ht + Gender + Smoke

Res.Df RSS Df Sum of Sq F Pr(>F)

1 651 28.920

2 649 13.734 2 15.186 358.82 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

More generally, consider ﬁtting two nested models, say Model A and

Model B, with systematic components

Model A: ˆμ

= β

+ β

+ ···+ β

Model B: ˆμ

= β

+ β

+ ···+ β

Model A is nested in Model B, because Model A is obtained by setting

,...,β

= 0 in Model B. The diﬀerence between the rss computed

for each model is the ss due to the diﬀerence between the models, based

on p



− p



degrees of freedom. Assuming H

: β

= ··· = β

=0is

2.10 Comparing Nested Models 63

true, the models are identical and ss is equivalent to residual variation. The

test-statistic is

F =

(rss

− rss

)/(p



− p



)

/(p



− p



)

rss

/(n − p



)

. (2.30)

A P -value is deduced by referring to an F -distribution with (p



−p



,n−p



)

degrees of freedom.

2.10.2 Sequential Analysis of Variance

The analysis of variance table just described is useful for comparing any two

nested models. Commonly, a sequence of nested models is compared. For each

pair of nested models in the sequence, the change in the rss (the ) and the

corresponding change in the degrees of freedom are recorded and organised

in a table.

As an example, consider model LC.B ﬁtted to the lungcap data

(Sect. 2.10.1,p.61), which explores the relationship between FEV and Smoke,

with the extraneous variables Age, Ht and Gender. A sequence of nested

models could be compared:

> LC.0 <- lm( log(FEV) ~ 1, data=lungcap) # No explanatory variables

> LC.1 <- update(LC.0,.~.+Age) # Age

> LC.2 <- update(LC.1,.~.+Ht) #AgeandHeight

> LC.3 <- update(LC.2,.~.+Gender) # Age, Height and Gender

> LC.4 <- update(LC.3,.~.+Smoke) # Then, add smoking status

Notice the use of update() to update models. To update model LC.0 to form

model LC.1, specify which components of LC.0 should be changed. The ﬁrst

input is the model to be changed, and the second is the component of the

model speciﬁcation to change. Here we wish to change the formula given in

LC.0. The left-hand side of the formula remains the same (as speciﬁed by .)

but the original right-hand side (indicated by .)hasAge added. Of course,

LC.1 could be also speciﬁed directly.

The rss can be computed for each model:

> RSS.0 <- sum( resid(LC.0)^2 )

> RSS.1 <- sum( resid(LC.1)^2 )

> RSS.2 <- sum( resid(LC.2)^2 )

> RSS.3 <- sum( resid(LC.3)^2 )

> RSS.4 <- sum( resid(LC.4)^2 )

> RSS.list <- c( Model4=RSS.4, Model3=RSS.3, Model2=RSS.2,

Model1=RSS.1, Model0=RSS.0)

> RSS.list

Model4 Model3 Model2 Model1 Model0

13.73356 13.83627 13.98958 29.31586 72.52591

64 2 Linear Regression Models

Notice that the rss reduces as the models become more complex. The change

in the rss,thess, can also be computed:

> SS.list <- diff(RSS.list); SS.list

Model3 Model2 Model1 Model0

0.1027098 0.1533136 15.3262790 43.2100549

The changes in the degrees of freedom between these nested models are all one

in this example. As before, we compare these changes in rss to an estimate

of σ

= mse, using the F -statistic (2.30):

> s2 <- summary(LC.4)$sigma^2 # One way to get MSE

> F.list <- (SS.list / 1) / s2; F.list

Model3 Model2 Model1 Model0

4.853708 7.245064 724.266452 2041.956379

> P.list <- pf( F.list, 1, df.residual(LC.4), lower.tail=FALSE)

> round(P.list, 6)

Model3 Model2 Model1 Model0

0.027937 0.007293 0.000000 0.000000

These computations are all performed in r by using anova(), and providing

as input the ﬁnal model in the set of nested models:

> anova(LC.4)

Analysis of Variance Table

Response: log(FEV)

Df Sum Sq Mean Sq F value Pr(>F)

Age 1 43.210 43.210 2041.9564 < 2.2e-16 ***

Ht 1 15.326 15.326 724.2665 < 2.2e-16 ***

Gender 1 0.153 0.153 7.2451 0.007293 **

Smoke 1 0.103 0.103 4.8537 0.027937 *

Residuals 649 13.734 0.021

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The F -values and P -values are the same as those found in the calculations

above.

This discussion shows that a series of sequential tests is performed. The

last formally tests if Smoke is signiﬁcant in the model, given that Age, Ht

and Gender are already in the model. In other words, the F-test for Smoke

adjusts for Age, Ht and Gender. In general, the F -tests in sequential anova

tables are always adjusted for all previous terms in the model.

Because the F -tests are adjusted for other terms in the model, numerous

F -tests are possible to test for the eﬀect of Smoke, depending on the order

in which the corresponding nested models are compared. For example, tests

based on Smoke include:

•TestforSmoke without adjusting for any other explanatory variables;

•TestforSmoke after ﬁrst adjusting for Age;

•TestforSmoke after ﬁrst adjusting for Ht;

•TestforSmoke after ﬁrst adjusting for both Age and Gender.

2.10 Comparing Nested Models 65

These tests consider diﬀerent hypotheses regarding Smoke so may produce

diﬀerent results. In contrast, t-tests (Sect. 2.8.3) present the same information

after all explanatory variables are in the model whatever order the variables

are added, as t-tests are adjusted for all other variables in the ﬁnal model.

Because the t-tests of Sect. 2.8.3 always adjust for all other terms in the

model, the results from the t-andF -tests are generally diﬀerent. However

the ﬁnal F -test in a sequential anova table, if it is on 1 degree of freedom,

is equivalent to the corresponding two-sided t-test. For example, the P -value

for Smoke in the above anova table (P =0.0279) is the same as the P -value

for Smoke given in Sect. 2.8.3, and the F -statistic for Smoke is the square of

the t-statistic for Smoke. In general, the square of a t-statistic on ν degrees of

freedom yields an F -statistic on (1,ν) degrees of freedom, so any two-sided

t-test can be expressed as an F-test.

The anova table shows the results of F -tests for the variables in the

presented order. The models higher in the table are special cases of the models

lower in the table (that is, models higher in the table are nested within models

lower in the table). The order in which the explanatory variables are ﬁtted is

important, except in very special cases (usually in an experiment explicitly

designed to ensure the order of ﬁtting is not important).

More generally, testing a series of sequential models is equivalent to sep-

arating the systematic component into contributions from each explanatory

variable (Table 2.4).

Example 2.20. Model LC.4 (in Sect. 2.10.2) ﬁts the explanatory variables Age,

Ht, Gender and Smoke in that order (data set: lungcap

). Consider ﬁtting the

explanatory variables in reverse order:

> LC.4.rev <- lm(log(FEV) ~ Smoke + Gender + Ht + Age, data=lungcap)

> anova(LC.4.rev)

Tabl e 2 . 4 The general form of an analysis of variance table for a normal linear re-

gression model, separating the systematic component into the contributions for each

explanatory variable (Sect. 2.10.2)

Mean

Source of variation ss df square F

⎧

⎪

⎨

⎪

⎩

Due to x

ss(x

)df

mse

Due to x

(adjusted for x

) ss(x

)df

mse

Due to x

(adjusted for x

and x

) ss(x

)df

mse

Due to x

(adjusted for x

,...,x

p−1

) ss(x

,...,x

p−1

)df

mse

Due to randomness rss n − p



mse

Total variation sst n − 1

66 2 Linear Regression Models

Analysis of Variance Table

Response: log(FEV)

Df Sum Sq Mean Sq F value Pr(>F)

Smoke 1 4.334 4.334 204.790 < 2.2e-16 ***

Gender 1 2.582 2.582 122.004 < 2.2e-16 ***

Ht 1 50.845 50.845 2402.745 < 2.2e-16 ***

Age 1 1.032 1.032 48.783 7.096e-12 ***

Residuals 649 13.734 0.021

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The level of signiﬁcance of Smoke depends on whether this variable is added

ﬁrst (model LC.4) or last, after adjusting for Age, Ht and Gender. Sometimes,

a variable may be signiﬁcant when added ﬁrst, but not at all signiﬁcant when

added after other variables. Thus the eﬀect of a variable may depend on

whether or not the model is adjusted for other variables. 

2.10.3 Parallel and Independent Regressions

Section 2.10.1 discussed the general case of testing any two nested models. We

now discuss a particular set of nested models that are commonly compared,

using the lung capacity data lungcap. For simplicity, we consider the case of

one covariate (height x

) and one factor (smoking status x

) to ﬁx ideas.

A naive (and obviously untrue) model is that μ = E[log(fev)] does not

depend on smoking status or height (Fig. 2.7,p.68, top left panel). The ﬁtted

systematic component is

ˆμ =0.9154, (2.31)

with rss =72.53 on 653 degrees of freedom. Note that this model simply

estimates the mean value of y = log(fev):

> mean(log(lungcap$FEV))

[1] 0.915437

To consider if the inﬂuence of height x

on μ = E[log(fev)] is signiﬁcant,

the ﬁtted model is (Fig. 2.7, top right panel)

ˆμ = −2.271 + 0.05212x

, (2.32)

with rss =14.82 on 652 degrees of freedom. This regression model does not

diﬀerentiate between smokers and non-smokers. Is the relationship diﬀerent

for smokers and non-smokers?

To consider this, add smoking status x

as an explanatory variable

(Fig. 2.7, bottom left panel):

ˆμ = −2.277 + 0.05222x

− 0.006830x

, (2.33)

2.10 Comparing Nested Models 67

with rss =14.82 on 651 degrees of freedom, and where x

= 0 refers to non-

smokers and x

= 1 to smokers. Using (2.33), the two separate systematic

components are

ˆμ =



−2.277 + 0.05222x

for non-smokers (set x

=0)

−2.284 + 0.05222x

for smokers (set x

=1)

with diﬀerent intercepts. Model (2.33) produces two parallel regression lines;

only the intercepts diﬀer but are so similar than the two lines can hardy be

distinguished on the plot (Fig. 2.7, bottom left panel). This model assumes

two separate systematic components, but a common random component and

so a common estimate of σ

Notice that the regression equation intercepts for smokers and non-smokers

are the same if the coeﬃcient for x

is zero. Hence, to formally test if the

intercepts are diﬀerent, a test of the corresponding β is conducted. In r:

> printCoefmat(coef(summary(lm( log(FEV) ~ Ht + Smoke, data=lungcap))))

Estimate Std. Error t value Pr(>|t|)

(Intercept) -2.2767801 0.0656677 -34.6712 <2e-16 ***

Ht 0.0522196 0.0010785 48.4174 <2e-16 ***

SmokeSmoker -0.0068303 0.0205450 -0.3325 0.7397

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The evidence suggests that diﬀerent intercepts are not needed when the slopes

of the lines are common. This is not unexpected given Fig. 2.7.

Perhaps the relationships between μ = E[log(fev)] and height have diﬀer-

ent intercepts and slopes for smokers and non-smokers also (Fig 2.7, bottom

right panel). Diﬀerent slopes can be modelled using the interaction between

height and smoking status as an explanatory variable:

ˆμ = −2.281 + 0.05230x

− 0.002294x

interaction

  

0.002294x

, (2.34)

with rss =14.82 on 650 degrees of freedom. Model (2.34) produces two sep-

arate systematic components; both the intercepts and slopes diﬀer (Fig. 2.7,

bottom right panel):

ˆμ =



−2.281 + 0.05230x

for non-smokers (set x

=0)

−2.137 + 0.05000x

for smokers (set x

=1).

This is not equivalent to ﬁtting two separate linear regression models, since

the same estimate of σ

is shared by both systematic components.

Notice that the regression equation slopes for smokers and non-smokers

are the same if the coeﬃcient for the interaction between x

and x

is zero.

Hence, to formally test if the slopes are diﬀerent, a test of the corresponding

45 50 55 60 65 70 75

0.0

0.5

1.0

1.5

Constant term only

Height (cm)

log(FEV, in litres)

Non−smokers

Smokers

45 50 55 60 65 70 75

0.0

0.5

1.0

1.5

Single model

Height (cm)

log(FEV, in litres)

Non−smokers

Smokers

45 50 55 60 65 70 75

0.0

0.5

1.0

1.5

Parallel regressions

Height (cm)

log(FEV, in litres)

Non−smokers

Smokers

45 50 55 60 65 70 75

0.0

0.5

1.0

1.5

Two independent

systematic components

Height (cm)

log(FEV, in litres)

Non−smokers

Smokers

Fig. 2.7 The logarithm of fev plotted against height. Top left: log(fev) is constant;

top right: log(fev) depends on height only; bottom left: parallel regression lines; bottom

right: two independent lines (Sect. 2.10.3)

2.10 Comparing Nested Models 69

Tabl e 2.5 Summarizing Models (2.31)–(2.34) ﬁtted to the lung capacity data

(Sect. 2.10.3)

Source of variation ss df ms F

57.70 1 57.70 2 531

0.002516 1 0.002516 0.1104

0.003318 1 0.003318 0.1455

Due to randomness 14.82 650 0.02280

Total variation 72.53 653

β is conducted. r indicates the interaction between two explanatory variables

by joining the interacting variables with : (a colon).

> LC.model <- lm( log(FEV) ~ Ht + Smoke + Ht:Smoke, data=lungcap)

A model including all main eﬀects plus the interaction can also be speciﬁed

using * (an asterisk). The above model, then, could be speciﬁed equivalently

as:

> LC.model <- lm( log(FEV) ~ Ht * Smoke, data=lungcap)

There is no evidence to suggest that diﬀerent intercepts and slopes are needed

for smokers and non-smokers:

> printCoefmat(coef(summary(LC.model)))

Estimate Std. Error t value Pr(>|t|)

(Intercept) -2.2814140 0.0668241 -34.1406 <2e-16 ***

Ht 0.0522961 0.0010977 47.6420 <2e-16 ***

SmokeSmoker 0.1440396 0.3960102 0.3637 0.7162

Ht:SmokeSmoker -0.0022937 0.0060125 -0.3815 0.7030

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Models (2.31)–(2.34) represent four ways to use linear regression models to

model the relationship between μ = E[log(fev)], height and smoking status.

Notice that the models are nested, so the methods in Sect. 2.10.1 (p. 61)are

appropriate for comparing the models statistically (Sect. 2.10.3). In the order

in which the models are presented in Table 2.5, models higher in the table

are nested within models lower in the table.

The value of rss reduces as the models become more complex. r produces

similar output using the anova() command, using the ﬁnal model as the

input:

> anova(LC.model)

Analysis of Variance Table

Response: log(FEV)

Df Sum Sq Mean Sq F value Pr(>F)

Ht 1 57.702 57.702 2531.1488 <2e-16 ***

Smoke 1 0.003 0.003 0.1104 0.7398

70 2 Linear Regression Models

Ht:Smoke 1 0.003 0.003 0.1455 0.7030

Residuals 650 14.818 0.023

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The table indicates that the model including only Ht is hard to improve upon;

neither Smoke nor the interaction are statistically signiﬁcant.

This analysis shows that height is important in the model, but the impact

of smoking status is less assured. Of course, in this example, we have not even

considered age and gender, or even if the model above follows the necessary

assumptions. In any case, the analysis suggests that height has a larger eﬀect

on μ = E[log(fev)] than smoking status in youth.

2.10.4 The Marginality Principle

For the model ﬁtted above, suppose that the interaction between height and

smoking status was necessary in the model. Then, height and smoking status

main-eﬀects should be included in the model whether they are statistically

signiﬁcant or not. Interactions indicate variations of the main-eﬀect terms,

which makes no sense if the main eﬀects are not present. This idea is called

the marginality principle. This principle states that:

• If higher-order powers of a covariate appear in a model, then the lower

order power should also be in the model. For example, if x

is in a model

then x should be also. (If x

remains in the model but x is removed, then

the model is artiﬁcially constrained to ﬁtting a quadratic model that has

zero slope when x = 0, something which is not usually required.)

• If the interaction between two or more factors appears in the model, then

the individual factors and lower-order interactions should appear also.

• If the interaction between factors and covariates appears in the linear

model, then the individual factors and covariates should appear also.

2.11 Choosing Between Non-nested Models: AIC and

BIC

The hypothesis tests discussed in Sect. 2.10 only apply when the models being

compared are nested. However, sometimes researchers wish to compare non-

nested models, so those testing methods do not apply. This section introduces

quantities for comparing models that are not necessarily nested.

First, recall that the two criteria for selecting a statistical model are ac-

curacy and parsimony (Sect. 1.10). The rss simply measures the accuracy:

adding a new explanatory variable to the model never makes the rss larger,

2.11 Choosing Between Non-nested Models: AIC and BIC 71

and almost always makes it smaller. Adding many explanatory variables pro-

duces smaller values of the rss, but also produces a more complicated model.

Akaike’s An Information Criterion (aic) balances these two criteria, by

measuring the accuracy using the rss but penalizing the complexity of the

model as measured by the number of estimated parameters. For a normal

linear regression model,

aic = n log(rss/n)+2p



(2.35)

when σ

is unknown. Using this deﬁnition, smaller values of the aic (closer

to −∞) represent better models. A formal, more general, deﬁnition for the

aic appears in Sect. 4.12. The term 2p



is called the penalty, since it penalizes

more complex linear regression models (models with larger values of p



)bya

factor of k = 2. Note that the value of the aic is not meaningful by itself; it

is useful for comparing models.

Other quantities similar to the aic are also deﬁned, with diﬀerent forms

for the penalty. One example is the Bayesian Information Criterion (bic),

also called Schwarz’s criterion [10]:

bic = n log(rss/n)+p



log n, (2.36)

when σ

is unknown. The bic is inclined to select lower dimensional (more

parsimonious) models than is aic, as the penalty for extra parameters is more

severe (k = log n>2) unless the number of observations is very small.

The aic and bic focus on the two diﬀerent purposes of a statistical model

(Sect. 1.9). The aic focuses more on creating a model for making good pre-

dictions. Extra explanatory variables may be included in the model if they

are more likely to help than not, even though the evidence for their im-

portance might not be convincing. The bic requires stronger evidence for

including explanatory variables, so produces simpler models having simpler

interpretations. aic is directed purely at prediction, while bic is a compro-

mise between interpretation and prediction. Neither aic nor bic are formal

testing methods, so no test statistics or P -values can be produced.

Both the aic and the bic are found in r using the extractAIC() com-

mand. The aic is returned by default, and the bic returned by specifying

the penalty k=log(nobs(fit)) where fit is the ﬁtted model, and nobs()

extracts the number of observations used to ﬁt the model.

Example 2.21. Consider the lung capacity data again (Example 1.1; data set:

lungcap). Suppose the researcher requires smoking status x

in the model,

and one of age x

or height x

. The two possible systematic components to

consider are

Model A: μ

= β

+ β

;

Model B: μ

= β

+ β

72 2 Linear Regression Models

The models are not nested, so the methods of Sect. 2.10 are not appropriate.

The aic is extracted using r as follows:

> LC.A <- lm( log(FEV) ~ Age + Smoke, data=lungcap )

> extractAIC(LC.A)

[1] 3.000 -2033.551

> LC.B <- lm( log(FEV) ~ Ht + Smoke, data=lungcap )

> extractAIC(LC.B)

[1] 3.000 -2470.728

The ﬁrst value reported is the equivalent degrees of freedom; for linear re-

gression models, the equivalent degrees of freedom is the number of estimated

regression parameters in the model. The aic is the second value reported;

thus the aic is lower (closer to −∞) for the second model which uses Ht.To

extract the bic, the same function extractAIC() is used, but the penalty is

adjusted:

> k <- log( length(lungcap$FEV) )

> extractAIC(LC.A,k=k)

[1] 3.000 -2020.102

> extractAIC(LC.B,k=k)

[1] 3.000 -2457.278

The bic is lower (closer to −∞) for the second model. The aic and the bic

both suggest the combination of Ht and Smoke is more useful as a set of

explanatory variables than the combination of Age and Smoke.Thisisnot

surprising, since Ht directly measures a physical trait. 

2.12 Tools to Assist in Model Selection

2.12.1 Adding and Dropping Variables

In situations where many explanatory variables are candidates for inclusion in

the model, selecting the optimal set is tedious and diﬃcult, especially because

the order in which the variables are added is usually important. Exploring

the possible models is more convenient using the r functions add1() and

drop1(). These functions explore the impact of adding one variable (add1())

and dropping one variable (drop1()) from the current model, one at a time.

The function step() repeatedly uses add1() and drop1() to suggest a model,

basing the decisions on the values of the aic (by default) or the bic.

Example 2.22. Consider the lung capacity data (data set: lungcap), and

the four explanatory variables Age, Ht, Gender and Smoke. The command

drop1() is used by providing a model, and each term is removed one at a

time:

2.12 Tools to Assist in Model Selection 73

> drop1( lm( log(FEV) ~ Age + Ht + Gender + Smoke, data=lungcap), test="F")

Single term deletions

Model:

log(FEV) ~ Age + Ht + Gender + Smoke

Df Sum of Sq RSS AIC F value Pr(>F)

<none> 13.734 -2516.6

Age 1 1.0323 14.766 -2471.2 48.7831 7.096e-12 ***

Ht 1 13.7485 27.482 -2064.9 649.7062 < 2.2e-16 ***

Gender 1 0.1325 13.866 -2512.3 6.2598 0.01260 *

Smoke 1 0.1027 13.836 -2513.7 4.8537 0.02794 *

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The output shows the value of the aic for the original model, and also when

Age, Ht, Gender and Smoke are removed from model one at a time. The aic

is the smallest (closest to −∞) when none of the explanatory variables are

removed (indicated by the row labelled <none>), suggesting no changes are

needed to the model. The F-test results for omitting terms are displayed

using test="F", otherwise drop1() reports only the aic.

In a similar fashion, using add1() adds explanatory variables one at a

time. Using add1() requires two inputs: the simplest and the most complex

systematic components to be considered. For the lung capacity data, we are

particularly interested in the relationship between fev and smoking status,

and so we ensure that the minimum model contains smoking status.

> LC.full <- lm( log(FEV) ~ Age + Ht + Gender + Smoke, data=lungcap)

> add1( lm( log(FEV) ~ Smoke, data=lungcap), LC.full, test="F" )

Single term additions

Model:

log(FEV) ~ Smoke

Df Sum of Sq RSS AIC F value Pr(>F)

<none> 68.192 -1474.5

Age 1 39.273 28.920 -2033.5 884.045 < 2.2e-16 ***

Ht 1 53.371 14.821 -2470.7 2344.240 < 2.2e-16 ***

Gender 1 2.582 65.611 -1497.8 25.616 5.426e-07 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The output shows that any one of the explanatory variables can be added

to the simple model log(FEV) ~ Smoke and improve the model (the aic

becomes closer to −∞). Since the aic is smallest when Ht is added, we would

add Ht to the systematic component, and then use add1() again. 

2.12.2 Automated Methods for Model Selection

If many explanatory variables are candidates for inclusion in a statistical

model, many statistical models are possible. For example, with ten possible

74 2 Linear Regression Models

explanatory variables, 2

= 1024 models are possible, ignoring possible in-

teractions. While comparing every possible model is an option, theory or

practical knowledge are usually used to reduce the number of model compar-

isons needed. Nevertheless, many comparison may still be made, and so the

task may be automated using computer software based on speciﬁc rules. The

three most common automated procedures for selecting models are forward

regression, backward elimination and stepwise regression.

Forward regression starts with essential explanatory variables in the model

(often just the constant β

), and each explanatory variable not in the current

model is added one at a time. If adding any variables improves the current

model, the variable making the greatest improvement is added, and the pro-

cess is repeated with the remaining variables not in the model. At each step,

the aic closest to −∞ is adopted. (The bic can be used by setting the appro-

priate penalty.) The process is repeated with all explanatory variables not in

the model until the model cannot be improved by adding more explanatory

variables.

Backward elimination is similar but removes explanatory variables at each

step. The process starts with all explanatory variables in the model, and at

each step removes each explanatory variables in the current model one at

a time. If removing any variables improves the current model, the variable

making the greatest improvement is removed, and the process is repeated

with the remaining variables in the model. At each step, the model with the

aic closest to −∞ is adopted. The process is repeated with all explanatory

variables in the model until the model cannot be improved by removing more

explanatory variables.

At each step of stepwise regression, explanatory variables not in the model

are added one at a time, and explanatory variables in the current model are

removed one at a time. If adding or removing any variable improves the

current model, the variable making the greatest improvement is added or re-

moved as necessary, and the process is repeated. At each step the model with

the aic closest to −∞ is adopted. Interactions are only considered between

lower-order terms already in the current model, according to the marginality

principle (Sect. 2.10.4). For example, r only considers adding the interaction

Ht:Gender if both Ht and Gender are in the current model.

These procedures are implemented in the r function step(), which (by

default) uses the aic to select models. step() can perform forward regres-

sion (using the input argument direction="forward"), backward elimina-

tion (direction="backward") or stepwise regression (direction="both").

The output is often voluminous if many steps are needed to ﬁnd the ﬁnal

model and a large number of explanatory variables are being considered.

The step() function has three commonly-used inputs. The input object

and the input scope together indicate the range of models for r to consider,

and their use depends on which type of approach is used (as indicated by

direction); see Example 2.23 for a demonstration.

2.12 Tools to Assist in Model Selection 75

Example 2.23. Consider again the lung capacity data lungcap.First,consider

forward regression. The ﬁrst argument in step() is the minimal acceptable

model. From Example 2.22, no variables can be removed from the model

> min.model <- lm(log(FEV) ~ Age + Ht + Gender + Smoke, data=lungcap)

to improve the model, so we begin with this as the minimal model. We now

use step() to suggest a model for the lungcap data, considering models as

complex as:

> max.model <- lm( log(FEV) ~ (Smoke + Age + Ht + Gender)^2, data=lungcap)

which speciﬁes all two-way interactions between the variables.

The use of step() requires the minimum model and maximum model that

is to be considered to be speciﬁed. The output is voluminous, so is not shown.

> auto.forward <- step( min.model, direction="forward",

scope=list(lower=min.model, upper=max.model) )

The use of step() for backward elimination is similar:

> auto.backward <- step( max.model, direction="backward",

scope=list(lower=min.model, upper=max.model) )

The use of step() for stepwise regression (which uses add1() and drop1()

repeatedly) is also similar.

> auto.both <- step( min.model, direction="both",

scope=list(lower=min.model, upper=max.model) )

In this case, the three approaches produce the same models:

> signif( coef(auto.forward), 3 )

(Intercept) Age Ht GenderM SmokeSmoker

-1.9400 0.0234 0.0428 0.0293 -0.0461

> signif( coef(auto.backward), 3 )

(Intercept) SmokeSmoker Age Ht GenderM

-1.9400 -0.0461 0.0234 0.0428 0.0293

> signif( coef(auto.both), 3 )

(Intercept) Age Ht GenderM SmokeSmoker

-1.9400 0.0234 0.0428 0.0293 -0.0461

Again, we note that we have not considered if the model is appropriate.

The three methods do not always produce the same suggested model. To

explain, consider some explanatory variable x1. The variable x1 might never

enter the model using the forward and stepwise regression procedures, so

interactions with x1 are never even considered (using the marginality prin-

ciple). However in backward elimination, an interaction involving x1 might

not be able to be removed from the model, so x1 must remain in the model

(using the marginality principle). 

76 2 Linear Regression Models

2.12.3 Objections to Using Stepwise Procedures

Automated stepwise procedures may be convenient (and appear in most sta-

tistical packages), but numerous objections exist [6, §4.3]. The objections are

philosophical in nature (stepwise methods do not rely on any theory or under-

standing of the data; stepwise methods test hypothesis that are never asked,

or even of interest), or relate to multiple testing issues (standard errors of the

regression parameter estimates in the ﬁnal model are too low; P -values are

too small; conﬁdence intervals are too narrow; R

values are too high; the

distribution of the anova test statistic does not have an F -distribution; re-

gression parameter estimates are too large in absolute value; models selected

using automated procedures often do not ﬁt well to new data sets). Many au-

thors strongly recommend against using automated procedures. Comparing

all possible sub-models presents the same objections. Other methods may be

used to assist in model selection [3, 13].

2.13 Case Study

A study [15, 16] compiled data from 90 countries (29 industrialized; 61 non-

industrialized) on the average annual sugar consumption and the estimated

mean number of decayed, missing and ﬁlled teeth (dmft) at age 12 years

(Table 2.6; data set: dental). A plot of the data (Fig. 2.8, left panel) suggests

a relationship between dmft and sugar consumption. Also, whether or not

the country is industrialized or not seems important (Fig. 2.8, right panel):

> data(dental); summary(dental)

Country Indus Sugar DMFT

Albania : 1 Ind :29 Min. : 0.97 Min. :0.300

Algeria : 1 NonInd:61 1st Qu.:14.53 1st Qu.:1.600

Angolia : 1 Median :33.79 Median :2.300

Argentina: 1 Mean :30.14 Mean :2.656

Australia: 1 3rd Qu.:44.32 3rd Qu.:3.350

Austria : 1 Max. :63.02 Max. :8.100

(Other) :84

> plot( DMFT ~ Sugar, las=1, data=dental, pch=ifelse( Indus=="Ind", 19, 1),

xlab="Mean annual sugar consumption\n(kg/person/year)",

ylab="Mean DMFT at age 12")

> legend("topleft", pch=c(19, 1), legend=c("Indus.","Non-indus."))

> boxplot(DMFT ~ Indus, data=dental, las=1,

ylab="Mean DMFT at age 12", xlab="Type of country")

Consider ﬁtting the linear regression model, including interactions:

> lm.dental <- lm( DMFT ~ Sugar * Indus, data=dental)

> anova(lm.dental)

Analysis of Variance Table

2.13 Case Study 77

Tabl e 2 . 6 The estimated mean number of decayed, missing and ﬁlled teeth (dmft)at

age 12 years, and the mean annual sugar consumption (in kg/person/year, computed

over the ﬁve years prior to the survey) for 90 countries. The ﬁrst ﬁve observations for

both categories are shown (Sect. 2.13)

Industrialized Non-industrialized

Mean annual Mean annual

Country sugar consumption dmft Country sugar consumption dmft

Albania 22.16 3.4 Algeria 36.60 2.3

Australia 49.96 2.0 Angolia 12.00 1.7

Austria 47.32 4.4 Argentina 34.56 3.4

Belgium 40.86 3.1 Bahamas 34.40 1.6

Canada 42.12 4.3 Bahrain 34.86 1.3

0 102030405060

Mean annual sugar consumption

(kg/person/year)

Mean DMFT at age 12

Indus.

Non−indus.

Ind NonInd

Type of country

Mean DMFT at age 12

Fig. 2.8 Left panel: a plot of the mean number of decayed, missing and ﬁlled teeth

(dmft) at age 12 against the mean annual sugar consumption in 90 countries; right

panel: a boxplot showing a diﬀerence in the distributions between the mean dmft for

industrialized and non-industrialized countries (Sect. 2.13)

Response: DMFT

Df Sum Sq Mean Sq F value Pr(>F)

Sugar 1 49.836 49.836 26.3196 1.768e-06 ***

Indus 1 1.812 1.812 0.9572 0.33065

Sugar:Indus 1 6.674 6.674 3.5248 0.06385 .

Residuals 86 162.840 1.893

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

From this anova table, the eﬀect of sugar consumption is signiﬁcant without

adjusting for any other variables. The eﬀect of Indus is not signiﬁcant after

adjusting for Sugar. The interaction between sugar consumption and whether

78 2 Linear Regression Models

the country is industrialized is marginally signiﬁcant after adjusting for sugar

consumption and the industrialization. Consider the ﬁtted model:

> coef( summary( lm.dental ) )

Estimate Std. Error t value Pr(>|t|)

(Intercept) 3.90857067 1.28649859 3.0381461 0.003151855

Sugar -0.01306504 0.03014315 -0.4334332 0.665785323

IndusNonInd -2.74389029 1.32480815 -2.0711605 0.041341018

Sugar:IndusNonInd 0.06004128 0.03198042 1.8774386 0.063847913

This output indicates that the mean sugar consumption is not signiﬁcant

after adjusting for the other variables. Furthermore, the coeﬃcient for the

sugar consumption is negative (though not statistically signiﬁcant), suggest-

ing greater sugar consumption is associated with lower mean numbers of

dmft. Recall this interpretation is for Indus=="Ind" (that is, for industri-

alized countries, when Indus=0). For non-industrialized countries, the coeﬃ-

cient for sugar consumption is

> sum( coef(lm.dental)[ c(2, 4) ] )

[1] 0.04697624

For non-industrialized countries, the coeﬃcient for the sugar consumption is

positive. Plotting the two lines (using abline()) is informative (Fig. 2.9):

> dental.cf <- coef( lm.dental )

> abline(a=dental.cf[1], b=dental.cf[2], lwd=2, lty=1)

> abline(a=sum( dental.cf[c(1, 3)]), b=sum(dental.cf[c(2, 4)]),

lwd=2, lty=2)

0102030405060

Mean annual sugar consumption

(kg/person/year)

Mean DMFT at age 12

Industrialized

Non−industrialized

Fig. 2.9 A plot of the mean number of decayed, missing and ﬁlled teeth (dmft)at

age 12 and the mean annual sugar consumption in 90 countries showing the ﬁtted model

(Sect. 2.13)

2.14 Using R for Fitting Linear Regression Models 79

Both the intercept and slope for NonInd are computed as the sum of the

appropriate two coeﬃcients.

Both the anova F -test and the t-test show the interaction is of marginal

importance. In fact, the two tests are equivalent (for example, compare the

corresponding P -values). We decide to retain the interaction, so Sugar and

Indus must remain in the model by the marginality principle (Sect. 2.10.3).

How can the model be interpreted? For non-industrialized countries, in-

creasing average sugar consumption is related to increasing average num-

ber of dmft at age 12 in children. An increase in mean annual sugar

consumption of one kg/person/year is associated with a mean increase of

−0.01307 + 0.06004 = 0.04698 dmft in children at age 12. For industrialized

countries, the average number of dmft at age 12 appears to be unrelated

to sugar consumption. Since industrialized countries in general have superior

personal dental hygiene, dental facilities, and ﬂuoridation of water, the ef-

fect of sugar consumption on dmft may be reduced. However, note that the

data for the industrialized countries span a much narrower range of sugar

consumptions than those for non-industrialized countries:

> range( dental$Sugar[dental$Indus=="Ind"] ) # Industrialized

[1] 22.16 53.54

> range( dental$Sugar[dental$Indus=="NonInd"] ) # Non-industrialized

[1] 0.97 63.02

Note that the mean number of dmft is recorded for children at age 12

(that is, for individuals), but the sugar consumption is an average for the

whole population. This means that any connection between the sugar con-

sumption and number of dmft for individuals cannot be made. For example,

individuals who do not consume sugar may be those individuals with the

larger numbers of dmft. Assuming that the relationships observed for a

population also applies to individuals within the population is called the eco-

logical fallacy. Also, since the data are observational, no cause-and-eﬀect can

be inferred. Even though the regression model has been successfully ﬁtted,

closer inspection suggests the model can be improved (Sect. 3.15.1).

2.14 Using R for Fitting Linear Regression Models

An introduction to using r is given in Appendix A (p. 503). For ﬁtting

linear regression models, the function lm() is used, as has been demonstrated

numerous times in this chapter (Sects. 2.6 and 2.10.3 are especially relevant).

Common inputs to lm() are:

• formula: The ﬁrst input is the model formula, taking the form y~x1

+ x2 + x3 + x1:x2 as an example.

80 2 Linear Regression Models

• data: The data frame containing the variables may be given as an input

using the data argument (in the form data=lungcap).

• weights: The prior weights are supplied using the weights input argu-

ment. The default is to set all prior weights to one.

• subset: Sometimes a model needs to be ﬁtted to a subset of the data,

when the subset input is used. For example, to ﬁt a linear regression

model for only the females in the lung capacity data, use, for example

lm(log(FEV) ~ Age, data=lungcap, subset=(Gender=="F"))

since Gender=="F" selects females. Alternatively, the subset() function

can be used to create a data frame that is a subset of the original data

frame; for example:

lm(log(FEV) ~ Age, data=subset(lungcap, Gender=="F"))

Other inputs are also deﬁned; see ?lm for more information. The explanatory

variables in the formula are re-ordered so that all main eﬀects are ﬁtted before

any interactions. Furthermore, all two-variables interactions are ﬁtted, then

all three-variable interactions, and so on. Use terms() to ﬁt explanatory

variables in a given order.

The function update() updates a model. Rather than specifying the model

completely, only the changes from a current model are given (see Sect. 2.10.1,

p. 61). Typical use: update(old, changes), where old is the old model, and

changes indicates the changes to the old model. Typically changes speciﬁes

a diﬀerent formula from the old model. The changes formula may contain

dots . on either side of the ~, which are replaced by the expression in the

old formula on the corresponding side of the formula.

Usually, the output from a ﬁtted model is sent to an output object:

fit <- lm( log(FEV) ~ Age + Ht + Gender + Smoke, data=lungcap),

for example. The output object fit contains substantial information; see

names(fit). The most useful information is extracted from fit using ex-

tractor functions, which include:

• coef(fit) (or coefficients(fit)) extracts the parameter estimates

;

• df.residual(fit) extracts the residual degrees of freedom;

• fitted(fit) (or fitted.values(fit)) extracts the ﬁtted values ˆμ.

Other useful r functions used with linear regression models include:

summary(fit):Thesummary() of the model prints the following: the pa-

rameter estimates with the corresponding standard errors, t-statistics

and two-tailed P -values for testing H

: β

= 0; the estimate of s;the

value of R

; the value of

; the results of the overall anova test for the

regression. See Fig. 2.6 (p. 51).

The output of summary() (for example, out <- summary(fit)) contains

substantial information (see names(out)). For example, out$r.squared

displays the value of R

and out$sigma displays the value of s. coef(out)

2.14 Using R for Fitting Linear Regression Models 81

displays the parameter estimates and standard errors, plus the t-values

and two-tailed P -values for testing H

: β

= 0. See ?summary.lm for

further information.

anova():Theanova() function can be used in two ways:

1. anova(fit): When a single model fit is given as input, an anova

table is produced that sequentially tests the signiﬁcance of each ex-

planatory variable as it is added to the model (Sect. 2.10.2).

2. anova(fit1, fit2, ...): Compares any set of ﬁtted nested mod-

els fit1, fit2 and so on by providing all models to anova().The

models are then tested against one another in the speciﬁed order,

where models earlier in the list of models are nested in later models

(Sect. 2.10.1).

confint(fit): Returns the 95% conﬁdence interval for all the regression co-

eﬃcients β

in the systematic component. For diﬀerent conﬁdence levels,

use confint(fit, level=0.99), for example, which creates 99% conﬁ-

dence intervals.

drop1() and add1(): Drops or adds explanatory variables one at a time from

the given model using the aic by default, while obeying the marginality

principle. F -test results are displayed by using test="F".Touseadd1(),

the second input shows the maximum scope of the models to be consid-

ered

step(): Uses automated methods for suggesting a linear regression model

based on the aic by default. Common usage is step(object, scope,

direction), where direction is one of "forward" for forward regres-

sion, "backward" for backward elimination, or "both" for stepwise re-

gression. object is an initial linear regression model, and scope deﬁnes

extent of the models to be considered. Section 2.12.2 (p. 73) demonstrates

the use of step() for the three types of automated methods. Decisions

can be based on the bic by using the input k=log(nobs(fit)), where

fit is the ﬁtted model.

extractAIC(fit): Returns the number of estimated regression parame-

ters as the ﬁrst output value, and the aic for the given model as

the second output value. To compute the bic instead of the aic,use

extractAIC(fit, k=log(nobs(fit))), where fit is the ﬁtted model.

abline(): Draws a straight line on the current plot. In the form abline(a=

2, b=-3), the straight line with intercept 2 and slope −3isdrawn.Fora

simple linear regression model, the slope and intercept are returned using

coef(fit), so that abline(coef(fit)) draws the systematic component

of the ﬁtted simple linear regression model. The form abline(h=1) draws

a horizontal line at y = 1, and the form abline(v=-1) draws a vertical

line at x =

−1.

82 2 Linear Regression Models

2.15 Summary

Chapter 2 focuses on linear regression models. These models have the form

(Sect. 2.2):

⎧

⎪

⎨

⎪

⎩

var[y

]=σ

= β



j=1

where E[y

]=μ

,thew

are known positive prior weights, σ

is the unknown

variance, and β

,...,β

are the unknown regression parameters. There are p

explanatory variables, and p



parameters β

to be estimated.

Special names are given in special cases (Sect. 2.2):

• Simple linear regression models refer to the case with p =1;

• Ordinary linear regression models have all prior weights set to one (to be

distinguished from weighted linear regression models);

• Multiple linear regression models refer to cases where p>1;

• Normal linear regression models refers to models with the additional as-

sumption that y

∼ N(μ

,σ

) (Sect. 2.8.1).

Matrix notation can be used to write these models compactly (Sect. 2.5.1).

The parameters β

in the linear regression model are estimated using least-

squares estimation, by minimizing the sum of the squared deviations between

and μ

(Sect. 2.4). These estimates are denoted

. The residual sum-of-

squares is rss =



i=1

− ˆμ

)

, where ˆμ



j=1

are called

the ﬁtted values (Sect. 2.4).

For simple linear regression, formulae exist for computing the least-squares

estimates of the regression parameters (Sect. 2.3.2). More generally, the val-

ues of

,...,

are estimated using matrix algebra (Sect. 2.4). In practice,

linear regression models are ﬁtted in r using lm() (Sect. 2.6). The estimated

regression parameters have standard error se(

) (Sects. 2.3.4 and 2.5.4).

An unbiased estimate of the variance of the randomness (Sect. 2.4.2)is

= rss/(n − p



), where n − p



is called the residual degrees of freedom.

To perform inference, it is necessary to also assume that the responses

follow a normal distribution, so that y

∼ N(μ

,σ

). Under this assump-

tion, the

have a normal distribution (Sect. 2.8.2), and a test of H

: β

= β

(for some given value β

) against a one- or two-tailed alternative can be per-

formed using a t-test (Sect. 2.8.3). Furthermore, a 100(1 − α)% conﬁdence

interval for β

can be formed using

± t

∗

α/2,n−p



se(

), where t

∗

α/2,n−p



the value of t on n − p



degrees of freedom such that an area α/2isineach

tail (Sect. 2.8.4).

The signiﬁcance of the regression model as a whole can be assessed by

comparing the ratio of the variation due to the systematic component to the

variation due to the random component, using an F -test (Sect. 2.9).

2.15 Summary 83

Each observation can be separated into a component predicted by the

model, and the residual: Data = Fit + Residual. In terms of sums of

squares, sst = ssReg + rss. Then, the multiple R

measures the proportion

of the total variation explained by the systematic component (Sect. 2.9): R

ssReg/sst. The adjusted R

, denoted

, modiﬁes R

to adjust for the

number of explanatory variables.

Any two nested models can be compared using an F -test (Sect. 2.10.1).

The signiﬁcance of individual explanatory variables can be tested sequen-

tially using F -tests by partitioning the sum-of-squares due to the systematic

component into contributions for each explanatory variable (Sect. 2.10.2).

An important application of nested models is testing for parallel and inde-

pendent regressions (Sect. 2.10.3). For non-nested models, comparisons are

possible using the aic and bic (Sect. 2.11).

Some tools are available to help with model selection, but must be used

with extreme caution (Sect. 2.12.3). The r functions drop1() and add1()

drop or add (respectively) explanatory variables one at a time from a model

(Sect. 2.12.1). Forward regression, backward elimination and step-wise selec-

tion procedures are automated procedures for choosing models (Sect. 2.12.2).

Finally, any regression coeﬃcients should be interpreted within the limi-

tations of the model and the data (Sect. 2.7).

Problems

Selected solutions begin on p. 530. Problems preceded by an asterisk * refer

to the optional sections in the text, and may require matrix manipulations.

2.1. In this problem, we consider two ways of writing the systematic compo-

nent of a simple linear regression model.

1. Interpret the meaning of the constant term β

when the systematic com-

ponent is written as μ = β

+ β

2. Interpret the meaning of the constant term α

when the systematic com-

ponent is written as μ = α

+ β

(x − ¯x).

2.2. For simple linear regression, show that the simultaneous solutions to

∂S/∂β

=0and∂S/∂β

=0in(2.4) and (2.5) produce the solutions shown

in (2.6) and (2.7)(p.37).

*2.3.In the case of simple linear regression with all weights set to one,

show that

WX =







where the summations are over i =1, 2,...,n. Hence, show that



xy −



y/n



− (



84 2 Linear Regression Models

*2.4.Show that the least-squares estimator of β in the linear regression model

β =(X

WX)

−1

Wy, by following these steps.

1. Show that S =(y−Xβ)

W(y−Xβ)=y

Wy−2β

Wy+β

WXβ.

S is the sum of the squared deviations.

2. Diﬀerentiate S with respect to β to ﬁnd dS/dβ.(Hint: Diﬀerentiating

Mβ with respect to β for any compatible matrix M gives 2Mβ.)

3. Use the previous result to ﬁnd the value of

β minimizing the value of S.

2.5. For simple linear regression, show that

deﬁned by (2.7) is an unbiased

estimator of β

.Thatis,showthatE[

]=β

.(Hint:



−¯x)a =0for

any constant a.)

*2.6.Show that

β =(X

WX)

−1

Wy is an unbiased estimator of β. That

is,showE[

β]=β.

*2.7.Show that the variance–covariance matrix of

β is var[

β]=(X

WX)

−1

using that var[Cy] = Cvar[y]C

for a constant matrix C.

2.8. Show that the F -statistic (2.28)andR

(2.29) are related by

F =

/(p



− 1)

(1 − R

)/(n − p



)

*2.9.Consider a simple linear regression model with systematic component

μ = β

+ β

x. Suppose we wish to design an experiment with n = 5 observa-

tions, when σ

is known to be 1. Suppose three designs for the experiment are

considered. In Design A, the values of the explanatory variable are x =1,1,

−1, −1 and 0. In Design B, the values are x =1,1,1,1and−1. In Design C,

the values are x =1,0.5, 0, −0.5and−1.

1. Write the model matrix X for each design.

2. Compute var[ˆμ] for each design.

3. Plot var[ˆμ]forx

between −1 and 1. When would Design A be preferred,

and why? When would Design B be preferred, and why? When would

Design C be preferred, and why?

2.10. Assume that a quantitative response variable y and a covariate x are

related by some smooth function f such that μ = f(x) where μ =E[y].

1. Assuming that the necessary derivatives exist, ﬁnd the ﬁrst-order Taylor

series expansion of f (x) expanded about ¯x, where ¯x is the mean of x.

2. Rearrange this expression into the form of a multiple regression model.

3. Explain how this implies that regression models are locally linear.

2.15 Summary 85

2.11. In Sect. 2.7, an interpretation for a model with systematic component

μ = E[log y]=β

+ β

x was discussed.

1. Use a Taylor series expansion of log y about μ =E[y].

2. Find the expected value of both sides of this equation, and hence show

that E[log y] ≈ log E[y] = log μ.

3. Using this information, show that an increase in the value of x by 1 is

associated (approximately) with a change in μ by a factor of exp(β

2.12. Using r, produce a vector of 30 random numbers y from a standard

normal distribution (use rnorm()). Generate a second vector of 30 random

numbers x from a standard normal distribution. Find the P -value for testing

if the explanatory variable x is signiﬁcantly related to y using the regression

model lm(y ~ x).

Repeat the process a large number of times, say 1000 times. What propor-

tion of the P -values are less than 5%? Less than 10%? What is the lesson?

2.13. A study [7] exposed sleeping people (males and females) of various

ages to four diﬀerent ﬁre cues (a crackling noise, a shuﬄing noise, a ﬂickering

light, an unpleasant smell), and recorded the response time (in seconds) for

the people to wake. Use the partially complete anova table (Table 2.7)to

answer the following questions.

1. Determine the degrees of freedom omitted from Table 2.7.

2. Determine how many observations were used in the analysis.

3. Find an unbiased estimate of σ

4. Determine which explanatory variables are statistically signiﬁcant for pre-

dicting response time, using sequential F -tests.

5. The analysed data are for participants who actually woke during the

experiment; some failed to wake at all and were omitted from the analysis.

Explain how this aﬀects the interpretation of the results.

6. Compute the aic for the three nested models implied by Table 2.7. What

model is suggested by the aic?

7. Compute the bic for the three nested models implied by Table 2.7. What

model is suggested by the bic?

8. Compute R

and the adjusted R

for the three models implied by

Table 2.7. What model is suggested by the R

and the adjusted R

Tabl e 2.7 An anova table for ﬁtting a linear regression model to the response time as

a function of various ﬁre cues and extraneous variables (Problem 2.13)

Source of variation df ss

Cue ? 117,793

Sex ? 2659

Age 3 22,850

Residual 60 177,639

86 2 Linear Regression Models

Tabl e 2.8 The parameter estimates and the standard errors in the linear regression

model for estimating the systolic blood pressure (in mm Hg) in Ghanaian men aged

between 18 and 65 (Problem 2.14)

Explanatory variable

se(

)

Constant 100.812 13.096

Age (in years) 0.332 0.062

Waist circumference (in cm) 0.411 0.090

Alcohol (yes: 1; no: 0) −3.003 1.758

Smoking (yes: 1; no: 0) −0.362 2.732

Ambient temperature (in

◦

C) −0.521 0.262

9. Compare the models suggested by the anova table, the aic,thebic, R

and the adjusted R

. Comment.

2.14. Numerous studies have shown an association between seasonal ambient

temperature (in

◦

C) and blood pressure (in mm Hg). A study of 574 rural

Ghanaian men aged between 18 and 65 studied this relationship [9] (and also

included a number of extraneous variables) using a linear regression model,

producing the results in Table 2.8.

1. Compute the P -values for each term in the model, and comment.

2. After adjusting for age, waist circumference, alcohol consumption and

smoking habits, describe the relationship between ambient temperature

and systolic blood pressure.

3. Plot the line describing the relationship between ambient temperature

and systolic blood pressure for 30-year-old men who do not smoke, do

drink alcohol and have a waist circumference of 100 cm. The authors

state that

Daily mean temperatures range between an average minimum of 20

◦

Cinthe

rainy season and an average maximum of 40

◦

C in the dry season. In the dry

season, early mornings are usually cool and the afternoons commonly hot

with daily maximum temperatures going as high as 45

◦

C (p. 17).

Use this information to guide your choice of temperature values for

your plot.

4. Compute a 95% conﬁdence interval for the regression parameter for am-

bient temperature.

5. Interpret the relationship between ambient temperature and all the vari-

ables in the regression equation.

6. Predict the mean systolic blood pressure for 35 year-old Ghanaian men

(who do not smoke, do drink alcohol and have a waist circumference of

100 cm) when the ambient temperature is 30

◦

2.15. An experiment was conducted [11] to determine how to maximize Mer-

maid meadowfoam ﬂower production (Table 2.9; data set: flowers) for ex-

traction as vegetable oil.

2.15 Summary 87

Tabl e 2.9 The average number of ﬂowers per meadowfoam plant (based on ten

seedlings) exposed to various levels of lighting at two diﬀerent times: at photoperiodic

ﬂoral induction (pfi)or24daysbeforepfi. These data are consistent with the results

in [11] (Problem 2.15)

Light intensity (in μmol m

−2

−1

)

Timing 150 300 450 600 750 900

At pfi 62.4 77.1 55.7 54.2 49.5 62.0 39.3 45.3 30.9 45.2 36.8 42.2

Before pfi 77.7 75.4 68.9 78.2 57.2 70.9 62.9 52.1 60.2 45.6 52.5 44.1

1. Plot the average number of ﬂowers produced per plant against the light

intensity, distinguishing the two timings. Comment.

2. Suppose a model with the systematic component Flowers ~ Light +

Timing was needed to model the data. What would such a systematic

component imply about the relationship between the variables?

3. Suppose a model with the systematic component Flowers ~ Light *

Timing was needed to model the data. What would such a systematic

component imply about the relationship between the variables?

4. Fit the two linear regression models with the systematic components

speciﬁed above. Which is the preferred model?

5. The ﬁtted model should use all prior weights as w

= 10 for all i. What

diﬀerence does it make if the prior weights are not deﬁned (which r

interprets as w

= 1 for all i)?

6. Plot the systematic component of the preferred regression model on the

data.

7. Interpret the model.

(This problem continues in Problem 3.13.)

2.16. A study of babies [1] hypothesized that babies would take longer to

learn to crawl in colder months because the extra clothing restricts their

movement. From 1988–1991, the babies’ ﬁrst crawling age and the average

monthly temperature six months after birth (when “infants presumably en-

ter the window of locomotor readiness”; p. 72) were recorded. The parents

reported the birth month, and age when their baby ﬁrst crept or crawled a

distance of four feet in one minute. Data were collected at the University of

Denver Infant Study Center on 208 boys and 206 girls, and summarized by

the birth month (Table 2.10; data set: crawl).

1. Plot the data. Which assumptions, if any, appear to be violated?

2. Explain why a weighted regression model is appropriate for the data.

3. Fit a weighted linear regression model to the data, and interpret the

regression coeﬃcients.

4. Formally test the hypothesis proposed by the researchers.

5. Find a 90% conﬁdence interval for the slope of the ﬁtted line, and

interpret.

88 2 Linear Regression Models

Tabl e 2.1 0 The crawling age and average monthly temperature six months after birth

for 414 babies (Problem 2.16)

Birth Mean age when Sample Monthly average temperature

month crawling started (weeks) size six months after birth (

◦

January 29.84 32 66

February 30.52 36 73

March 29.70 23 72

April 31.84 26 63

May 28.58 27 52

June 31.44 29 39

July 33.64 21 33

August 32.82 45 30

September 33.83 38 33

October 33.35 44 37

November 33.38 49 48

December 32.32 44 57

6. Fit the unweighted regression model, then plot both regression lines on

a plot of the data. Comment on the diﬀerences.

7. Compute the 95% conﬁdence intervals for the ﬁtted values from the

weighted regression line, and also plot these.

8. Interpret the model.

(This problem continues in Problem 3.15.)

2.17. For a sample of 64 grazing Merino castrated male sheep (wethers) [5,

14, 17], the daily energy requirements and weight was recorded (Table 2.11;

data set: sheep).

1. Fit a linear regression model to model the daily energy requirement from

the weight.

2. Plot the data, plus the systematic component of the ﬁtted model and the

95% conﬁdence intervals about the ﬁtted values.

3. Interpret the model.

4. Which assumptions, if any, appear to be violated? Explain.

(This problem continues in Problem 3.17.)

2.18. Children were asked to build towers out of cubical and cylindrical

blocks as high as they could [8, 12], and the number of blocks used and

the time taken were recorded (Table 2.12; data set: blocks). In this Prob-

lem, we focus on the time taken to build the towers. (The number of blocks

used to build towers is studied in Problem 10.19.)

1. The data were originally examined in Problem 1.9 (p. 28). Using these

plots, summarize the possible relationships of the explanatory variables

with the time taken. Which assumptions, if any, appear to be violated?

2.15 Summary 89

Tabl e 2. 1 1 The energy requirements (in Mcal/day) and weight (in kg) for a sample of

64 Merino wethers (Problem 2.17)

Weight Energy Weight Energy Weight Energy Weight Energy Weight Energy

22.1 1.31 25.1 1.46 25.1 1.00 25.7 1.20 25.9 1.36

26.2 1.27 27.0 1.21 30.0 1.23 30.2 1.01 30.2 1.12

33.2 1.25 33.2 1.32 33.2 1.47 33.9 1.03 33.8 1.46

34.3 1.14 34.9 1.00 42.6 1.81 43.7 1.73 44.9 1.93

49.0 1.78 49.2 2.53 51.8 1.87 51.8 1.92 52.5 1.65

52.6 1.70 53.3 2.66 23.9 1.37 25.1 1.39 26.7 1.26

27.6 1.39 28.4 1.27 28.9 1.74 29.3 1.54 29.7 1.44

31.0 1.47 31.0 1.50 31.8 1.60 32.0 1.67 32.1 1.80

32.6 1.75 33.1 1.82 34.1 1.36 34.2 1.59 44.4 2.33

44.6 2.25 52.1 2.67 52.4 2.28 52.7 3.15 53.1 2.73

52.6 3.73 46.7 2.21 37.1 2.11 31.8 1.39 36.1 1.79

28.6 2.13 29.2 1.80 26.2 1.05 45.9 2.36 36.8 2.31

34.4 1.85 34.4 1.63 26.4 1.27 27.5 0.94

Tabl e 2 .12 The time taken (in s), and the number of blocks used, to build towers out

of two shapes of blocks in two trials one month apart. The children’s ages are given in

decimal years (converted from years and months). The results for the ﬁrst ﬁve children

are shown (Prob. 2.18)

Trial 1 Trial 2

Cubes Cylinders Cubes Cylinders

Child Age Number Time Number Time Number Time Number Time

A 4.67 11 30.0 6 30.0 10 35.0 8 125.0

B 5.00 9 19.0 4 6.0 10 28.0 5 14.4

C 4.42 8 18.6 5 14.2 7 18.0 5 24.0

D 4.33 9 23.0 4 8.2 11 34.8 6 14.4

E 4.33 10 29.0 6 14.0 6 16.2 5 15.0

2. Suppose a model with the systematic component Time ~ Age * Shape

was needed to model the data. What would such a systematic component

imply about the relationship between the variables?

3. Suppose a model with the systematic component Time ~ Age * Trial

was needed to model the data. What would such a systematic component

imply about the relationship between the variables?

4. Suppose a model with the systematic component Time ~ (Age + Shape)

* Trial was needed to model the data. What would such a systematic

component imply about the relationship between the variables?

5. One hypothesis of interest is whether the time taken to build the tower

diﬀers between cubical and cylindrical shaped blocks. Test this hypothesis

by ﬁtting a linear regression model.

90 REFERENCES

Tabl e 2 .13 The sharpener data; the ﬁrst ﬁve cases are shown (Problem 2.13)

9.87 0.64 0.22 0.83 0.41 0.64 0.88 0.22 0.41 0.38 0.02

8.86 0.16 0.55 0.71 0.25 0.61 0.68 0.93 0.95 0.15 0.00

7.82 0.14 0.00 0.97 0.54 0.25 0.46 0.71 0.90 0.13 0.18

10.77 0.53 0.45 0.80 0.54 0.84 0.39 0.16 0.06 0.72 0.90

9.53 0.14 0.52 0.13 0.91 0.15 0.52 0.09 0.26 0.12 0.51

6. Another hypothesis of interest is that older children take less time to

build the towers than younger children, but the diﬀerence would depend

on the type of block. Test this hypothesis.

7. Find a suitable linear regression model for the time taken to build the

towers. Do you think this model is suitable? Explain.

8. Interpret your ﬁnal model.

(This problem continues in Problem 3.16.)

2.19. The data in Table 2.13 (data set: sharpener) come from a study to

make a point.

1. Using the forward regression procedure (Sect. 2.12.2,p.73), ﬁnd a suit-

able linear regression (without interactions) model for predicting y from

the explanatory variables, based on using the aic.

2. Using the backward elimination procedure, ﬁnd a model (without inter-

actions) for predicting y from the explanatory variables based on using

the aic.

3. Using the step-wise regression procedure, ﬁnd a model (without interac-

tions) for predicting y from the explanatory variables, based on using the

aic.

4. From the results of the above approaches, deduce a model (without in-

teractions) for the data.

5. Repeat the three procedures, but use the bic to select a model.

6. After reading the r help for the sharpener data (using ?sharpener),

comment on the use of automatic methods for ﬁtting regression models.

References

[1] Benson, J.: Season of birth and onset of locomotion: Theoretical and

methodological implications. Infant Behavior and Development 16(1),

69–81 (1993)

REFERENCES 91

[2] Bland, J.M., Peacock, J.L., Anderson, H.R., Brooke, O.G.: The adjust-

ment of birthweight for very early gestational ages: Two related problems

in statistical analysis. Applied Statistics 39(2), 229–239 (1990)

[3] Davison, A.C., Hinkley, D.V.: Bootstrap Methods and their Application.

Cambridge University Press (1997)

[4] Green, P.J.: Iteratively reweighted least squares for maximum likelihood

estimation, and some robust and resistant alternatives (with discussion).

Journal of the Royal Statistical Society, Series B 46(2), 149–192 (1984)

[5] Hand, D.J., Daly, F., Lunn, A.D., McConway, K.Y., Ostrowski, E.: A

Handbook of Small Data Sets. Chapman and Hall, London (1996)

[6] Harrell Jr, F.: Regression Modeling Strategies: With Applications to

Linear Models, Logistic Models, and Survival Analysis. Springer (2001)

[7] Hasofer, A.M., Bruck, D.: Statistical analysis of response to ﬁre cues.

Fire Safety Journal 39, 663–688 (2004)

[8] Johnson, B., Courtney, D.M.: Tower building. Child Development 2(2),

161–162 (1931)

[9] Kunutsor, S.K., Powles, J.W.: The eﬀect of ambient temperature on

blood pressure in a rural West African adult population: A cross-

sectional study. Cardiovascular Journal of Africa 21(1), 17–20 (2010)

[10] Schwarz, G.E.: Estimating the dimension of a model. The Annals of

Statistics 6(2), 461–464 (1978)

[11] Seddigh, M., Joliﬀ, G.D.: Light intensity eﬀects on meadowfoam growth

and ﬂowering. Crop Science 34, 497–503 (1994)

[12] Singer, J.D., Willett, J.B.: Improving the teaching of applied statistics:

Putting the data back into data analysis. The American Statistician

44(3), 223–230 (1990)

[13] Tibshirani, R.: Regression shrinkage and selection via the lasso. Journal

of the Royal Statistical Society. Series B (Methodological) 58(1), 267–

288 (1996)

[14] Wallach, D., Goﬃnet, B.: Mean square error of prediction in models for

studying ecological systems and agronomic systems. Biometrics 43(3),

561–573 (1987)

[15] Woodward, M.: Epidemiology: study design and data analysis, second

edn. Chapman & Hall/CRC, Boca Raton, FL (2004)

[16] Woodward, M., Walker, A.R.P.: Sugar consumption and dental caries:

Evidence from 90 countries. British Dental Journal 176, 297–302 (1994)

[17] Young, B.A., Corbett, J.L.: Maintenance energy requirement of grazing

sheep in relation to herbage availability. Australian Journal of Agricul-

tural Research 23(1), 57–76 (1972)

Chapter 3

Linear Regression Models:

Diagnostics and Model-Building

Normality is a myth; there never was, and never will be,

a normal distribution. This is an over-statement from the

practical point of view, but it represents a safer initial

mental attitude than any in fashion during the past two

decades.

Geary [13, p. 241]

3.1 Introduction and Overview

As the previous two chapters have demonstrated, the process of building

a linear regression model, or any regression model, is aided by exploratory

plots of the data, by reﬂecting on the experimental design, and by considering

the scientiﬁc relationships between the variables. This process should ensure

that the model is broadly appropriate for the data. Once a candidate model

has been ﬁtted to the data, however, there are specialist measures and plots

that can examine the model assumptions and diagnose possible problems in

greater detail. This chapter describes these tools for detecting and highlight-

ing violations of assumptions in linear regression models. The chapter goes

on to discuss some possible courses of action that might alleviate the identi-

ﬁed problems. The process of examining and identifying possible violations of

model assumptions is called diagnostic analysis. The assumptions of linear re-

gression models are ﬁrst reviewed (Sect. 3.2), then residuals, the main tools of

diagnostic analysis, are deﬁned (Sect. 3.3). We follow with a discussion of the

leverage, a measure of the location of an observation relative to the average

observation location (Sect. 3.4). The various diagnostic tools for checking the

model assumptions are then introduced (Sect. 3.5) followed by techniques for

identifying unusual and inﬂuential observations (Sect. 3.6). The terminology

of residuals is summarized in Sect. 3.7. Techniques for ﬁxing any weaknesses

in the models are summarised in Sect. 3.8, and explained in greater detail in

Sects. 3.9 to 3.13. Finally, the issue of collinearity is discussed (Sect. 3.14).

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_3

94 3 Linear Regression Models: Diagnostics and Model-Building

3.2 Assumptions from a Practical Point of View

3.2.1 Types of Assumptions

The general form of a linear regression model is given by (2.1) or, assuming

normality, by (2.25). The assumptions of the model can be summarized as:

• Lack of outliers: All responses were generated from the same process, so

that the same regression model is appropriate for all the observations.

• Linearity: The linear predictor captures the true relationship between μ

and the explanatory variables, and all important explanatory variables

are included.

• Constant variance: The responses y

have constant variance, apart from

known weights w

• Independence: The responses y

are statistically independent of each

other.

• Distribution: The responses y

are normally distributed around μ

Failure of the assumptions may lead to inappropriate and incorrect results

from hypothesis tests and conﬁdence intervals, potentially leading to incorrect

parameter estimation and incorrect interpretations.

The ﬁrst two assumptions are obviously the most basic. If the linear model

doesn’t correctly model the systematic trend in the responses, then it will be

useless for prediction and interpretation purposes. The other three assump-

tions aﬀect the precision with which the regression coeﬃcients are estimated,

as well as the accuracy of standard errors and the validity of statistical tests.

3.2.2 The Linear Predictor

This chapter generally assumes that all the important explanatory variables

are at least available. Methods will be presented for detecting observations

that are errors or which do not ﬁt the pattern of the remaining observations.

This chapter will also explore ways to improve linearity by changing the scale

of the covariate or response, or to accommodate more complex relationships

by building new covariates from the existing ones.

3.2.3 Constant Variance

Deviations from constant variance are of two major types. Firstly, it is pos-

sible that one group of observations is intrinsically more heterogeneous than

another. For example, diseased patients often show more variability than

3.2 Assumptions from a Practical Point of View 95

control patients without the disease, or disease tumour tissue may show

more variability than normal tissue. However, by far the most commonly-

arising and important scenario leading to non-constant variance is when the

response is measured on a scale for which the precision of the observation

depends on the size of the observation. Measures of positive physical quan-

tities frequently show more absolute variability when the quantity is large

than when the quantity is small. For example, the mass of a heavy object

might be measured to a constant relative error over a wide range of values, so

that the standard deviation of each measurement is proportional to its mean.

The number of people in a group might be counted accurately when there

are only a few individuals, but will have to be estimated more approximately

when the crowd is large. This sort of mean–variance relationship will be ex-

plored extensively in later chapters of this book; in fact it is a major theme

of the book. This chapter will examine ways to alleviate any mean–variance

relationship by transforming the response.

3.2.4 Independence

Ensuring that the responses y

are statistically independent is one of the aims

of the experimental design or data collection process. Dependence between

responses can arise because the responses share a common source or because

the data are collected in a hierarchical manner. Examples include:

• Repeated measures. Multiple treatments are applied to same experimen-

tal subjects.

• Blocking. A group of observations are drawn close in space or in time so

as to minimize their variability. For example, multiple plants are grown

in the same plot of ground, or a complex experiment is conducted in a

number of separate stages or batches.

• Multilevel sampling. For example, a cost-eﬀective way to sample school

children is to take a random sample of school districts; within selected

districts, take a random sample of schools; within selected schools, take

a random sample of pupils.

• Time series. The responses arise from observing the same process over

time. For example, the sales ﬁgures of a particular product.

In the simplest cases, the dependence between multiple observations in a

block can be accounted for by including the blocking variable as an explana-

tory factor in the linear model. For example, when multiple treatments are

given to the same set of subjects, the subject IDs may be treated as the

levels of an explanatory factor. In other cases, dependence can by detected

by suitable plots. In more complex cases, when there are multiple levels of

variability, random eﬀects models may be required to fully represent the data

collection process [29]. However, these are beyond the scope of this textbook.

96 3 Linear Regression Models: Diagnostics and Model-Building

3.2.5 Normality

The assumption of normality underlies the use of F -andt-tests (Sect. 2.8).

When the number of observations is large, and there are no serious outliers,

t-andF -tests tend to behave well even when the residuals are not normally

distributed. This means the assumption of normality is most critical for small

sample sizes. Unfortunately, small sample size is exactly the situation when

assessing normality is most diﬃcult.

3.2.6 Measurement Scales

A broad consideration that aﬀects many of the assumptions is that of the

measurement scales used for the response and the explanatory variables, and

especially the range of feasible values that the variables can take on. For

example, if the response y

can take only positive values, then it is clearly

mathematically impossible for it to follow a normal distribution. Similarly,

a positive response variable may cause problems if the linear predictor can

take negative values. A strictly positive random variable is also unlikely to

have a constant variance if values near zero are possible. The same sort of

considerations apply doubly when the response represents a proportion and

is therefore bounded at both zero and one. In this case, constant variance is

unlikely if values close to zero or one are possible. In general, linear models for

positive or constrained response variables may be ﬁne over a limited range of

values, but are likely to be suspect when the values range over several orders

of magnitude are possible.

The units of measurement can also guide the process of model building.

For the lung capacity data of Example 1.1, the response variable fev is in

units of volume, whereas height is in units of length. If individuals were of the

same general shape, volume would tend to be proportional to height cubed.

3.2.7 Approximations and Consequences

As always, a statistical model is a mathematical ideal, and will never be

an exact representation of any real data set or real physical process. When

evaluating the assumptions, we are guided by the likely sensitivity of the

conclusions to deviations from the model assumptions. For example, the re-

sponse variable y may not exactly be a linear function of a covariate x, but a

linear approximation may be adequate in a context where are limited range

of x values are likely to appear. The assumptions are ordered in the above

list from those that eﬀect the ﬁrst moment of the responses (the mean),

to the second moment (variances) to third and higher moments (complete

3.3 Residuals for Normal Linear Regression Models 97

distribution of y

). Generally speaking, assumptions that aﬀect the lower mo-

ments of y

are the most basic, and assumptions relating to higher moments

are progressively of lower priority.

3.3 Residuals for Normal Linear Regression Models

The raw residuals are simply

= y

− ˆμ

Recall that rss =



i=1

Since ˆμ is estimated from the data, ˆμ is a random variable. This means

that var[y

− ˆμ

] is not the same as var[y

− μ

]=var[y

]=σ

. Instead,

as shown in Sect. 3.4.2,

var[r

]=σ

(1 − h

)/w

, (3.1)

where h

is the leverage which y

has in estimating its own ﬁtted value ˆμ

(Sect. 3.4).

Equation (3.1) means that the raw residuals r

do not have constant vari-

ance, and so may be diﬃcult to interpret in diagnostic plots. A modiﬁed

residual that does have constant variance can be deﬁned by

∗

√

− ˆμ

)

√

1 − h

with var[r

∗

]=σ

. The modiﬁed residual has the interesting interpretation

that its square (r

∗

)

is the reduction in the rss that results when Observa-

tion i is omitted from the data (Problem 3.1).

After estimating σ

by s

,thestandardized residuals are deﬁned by



∗

√

− ˆμ

)

√

1 − h

. (3.2)

The standardized residuals estimate the standardized distance between the

data y

about the ﬁtted values ˆμ

. The standardized residuals are ap-

proximately standard normal in distribution. More exactly, r



follows a t-

distribution on n − p



degrees of freedom.

The raw residuals are computed from any ﬁtted linear regression model fit

in r using resid(fit), and standardized residuals using rstandard(fit).

Example 3.1. In Chaps. 1 and 2, the lung capacity were used (Example 1.5;

data set lungcap), and log(fev) was found to be linearly associated with

height. For this reason, models in those chapters were considered using the

response variable y = log(fev).

98 3 Linear Regression Models: Diagnostics and Model-Building

In this chapter, for the purpose of demonstrating diagnostics for linear

regression models, we begin by considering a model for y = fev (not y =

log(fev)) to show how the diagnostics reveal the inadequacies of this model.

We decide to use a systematic component involving Ht, Gender and Smoke.

(preferring Ht over Age as Ht is a physical trait).

> library(GLMsData); data(lungcap)

> lungcap$Smoke <- factor(lungcap$Smoke,

levels=c(0, 1),

labels=c("Non-smoker","Smoker"))

> ### POOR MODEL!

> LC.lm <- lm( FEV ~ Ht + Gender + Smoke, data=lungcap)

To compute the residuals for this model in r,use:

> resid.raw <- resid( LC.lm ) # The raw residuals

> resid.std <- rstandard( LC.lm ) # The standardized residuals

> c( Raw=var(resid.raw), Standardized=var(resid.std) )

Raw Standardized

0.1812849 1.0027232

The standardized residuals have variance close to one, as expected. 

3.4 The Leverages for Linear Regression Models

3.4.1 Leverage and Extreme Covariate Values

To explain the leverages clearly, we need ﬁrst to standardize the responses so

they have constant variance. Write the standardized responses as z

√

Then E[z

]=ν

√

and var[z

]=σ

. The ﬁtted values ˆν

√

ˆμ

can

be considered to be a linear function of the responses z

.Thehat-values are

deﬁned as those values h

that relate the responses z

to the ﬁtted values ˆν

satisfying

ˆν



j=1

The hat-value h

is the coeﬃcient applied to the standardized observation z

to obtain the standardized ﬁtted value ˆν

. When the weights w

are all one,

ˆμ

= h

+ h

+ ···+ h



j=1

This shows that the hat-value h

is the coeﬃcient applied to y

to obtain ˆμ

Colloquially, the hat-values put the “hat” on μ

3.4 The Leverages for Linear Regression Models 99

Of particular interest are the diagonal hat-values h

, which we will call

leverages, written h

= h

. The leverages h

measure the weight that response

(or z

) receives in computing its own ﬁtted value: h



j=1

.The

leverages h

depend on the values of the explanatory variables and weights,

not on the values of the responses. The n leverages satisfy 1/n ≤ h

≤ 1

(Problem 3.3), and have total sum equal to p



. This shows that the mean of

the hat-values is

h = p



/n.

In the case of simple linear regression without weights (Problem 3.3),

− ¯x)

showing that leverage increases quadratically as x

is further from the mean

¯x. It is a good analogy to think of ¯x as deﬁning the fulcrum of a lever through

which each observation contributes to the regression slope, with x

− ¯x the

distance of the point from the fulcrum.

For an unweighted linear regression with a factor as the single explana-

tory variable, the leverages are h

=1/n

, where n

is the total number of

observations in the same group as observation i.

In general, a small leverage for Observation i indicates that many observa-

tions, not just one, are contributing to the estimation of the ﬁtted value. In

the extreme case that h

=1,theith ﬁtted value will be entirely determined

by the ith observation, so that ˆμ

= y

. In practice, this means that large

values of h

(perhaps two or three times the mean value of the h

) identify

unusual combinations of the explanatory variables.

The leverages in r for a linear regression model called fit are computed

using the command hatvalues(fit).

Example 3.2. For the poor model ﬁtted in Example 3.1 to the lungcap data,

the leverages are found using hatvalues():

> h <- hatvalues( LC.lm ) # Produce the leverages

> sort( h, decreasing=TRUE) [1:2] # The largest two leverages

629 631

0.02207842 0.02034224

The two largest leverages are for Observations 629 and 631. Compare these

leverages to the mean value of the leverages:

> mean(h); length(coef(LC.lm))/length(lungcap$FEV) # Mean leverage

[1] 0.006116208

> sort( h, decreasing=TRUE) [1:2] / mean(h)

629 631

3.609822 3.325956

Observations 629 and 631 are many times greater than the mean value of

the leverages. Note that both of these large leverages correspond to male

smokers:

100 3 Linear Regression Models: Diagnostics and Model-Building

55 60 65 70 75

Male smokers

Height (inches)

FEV (L)

Large leverage points

Fig. 3.1 fev plotted against height for males smokers. The leverages h

are shown for

two observations as ﬁlled dots (Example 3.2)

> sort.h <- sort( h, decreasing=TRUE, index.return=TRUE)

> large.h <- sort.h$ix[1:2] # Provide the index where these occur

> lungcap[ large.h, ]

Age FEV Ht Gender Smoke

629 9 1.953 58 M Smoker

631 11 1.694 60 M Smoker

Consider the plot of FEV against Ht for just male smokers then:

> plot( FEV ~ Ht, main="Male smokers",

data=subset( lungcap, Gender=="M" & Smoke=="Smoker"),

# Only male smokers las=1, xlim=c(55, 75), ylim=c(0, 5),

xlab="Height (inches)", ylab="FEV (L)" )

> points( FEV[large.h] ~ Ht[large.h], data=lungcap, pch=19) # Large vals

> legend("bottomright", pch=19, legend=c("Large leverage points") )

The two largest leverages correspond to the two unusual observations in the

bottom left corner of the plot (Fig. 3.1). 

* 3.4.2 The Leverages Using Matrix Algebra

For simplicity, consider ﬁrst the case of unweighted regression for which all

the w

= 1; in other words W = I

. Recall that the least squares estimates

of the regression coeﬃcients are given by

β =(X

−1

y when W = I

Therefore the ﬁtted values are given by

μ =Xβ =Hy with

H=X(X

−1

We say that H is the hat matrix, because it puts the “hat” on y. The leverages

are the diagonal elements of H.

3.5 Residual Plots 101

Write r for the vector of raw residuals from the regression

r = y −

μ =(I

− H)y.

It is not hard to show that the covariance matrix of this residual vector is

given by

var[r]=(I

− H)σ

In particular, it follows that var[r

]=(1− h

)σ

To incorporate general weights W = diag(w

), it is easiest to transform to

an unweighted regression. Write z =W

1/2

y, and deﬁne X

1/2

X. Then

E[z]=ν =X

β and var[z]=σ

. The hat matrix for this linear model is

H=X

)

−1

1/2

X(X

WX)

−1

1/2

. (3.3)

For the transformed regression, var[z − ˆν]=σ

− H

). The residuals for

the weighted regression are r = W

−1/2

(z −

ν). It follows (Problem 3.2) that

the covariance matrix of the residuals for the weighted regression is

var[r]=var[y −

μ]=σ

−1/2

− H)

−1/2

In r, the leverages may be computed directly from the model matrix X using

hatvalues(X).

3.5 Residual Plots

3.5.1 Plot Residuals Against x

: Linearity

Basic exploratory data analysis usually includes a plot of the response variable

against each explanatory variable. Such a plot is complicated by the fact that

multiple explanatory variables may have competing eﬀects on the response.

Furthermore, some deviations from linearity may be hard to detect. A plot

of residuals against a covariate x

can more easily detect deviations from

linearity, because the linear eﬀects of all the explanatory variables have been

removed. If the model ﬁts well, the residuals should show no pattern, just

constant variability around zero for all values of x

. Any systematic trend in

the residuals, such as a quadratic curve, suggests a need to transform x

to include extra terms in the linear model.

Using scatter.smooth() in place of plot() in r adds a smoothing curve

to the plots, which may make trends easier to see.

Example 3.3. Consider again the lung capacity data (Example 1.1; data set:

lungcap), and model LC.lm ﬁtted to the data in Example 3.1. Assume the

102 3 Linear Regression Models: Diagnostics and Model-Building

45 50 55 60 65 70 75

−4

−2

Height (inches)

Standardized residuals

Fig. 3.2 Residuals plotted against the covariate Ht for the model LC.lm ﬁtted to the

lung capacity data (Example 3.3)

data were collected so that the responses are independent. Then, plots of

residuals against the covariate can be created:

> # Plot std residuals against Ht

> scatter.smooth( rstandard( LC.lm ) ~ lungcap$Ht, col="grey",

las=1, ylab="Standardized residuals", xlab="Height (inches)")

The plots of residuals against height (Fig. 3.2) are slightly non-linear, and

have increasing variance. This suggests that the model is poor. Of course,

linearity is not relevant for gender or smoking status, as these variables take

only two levels. 

3.5.2 Partial Residual Plots

Partial residuals plots are similar to plotting residuals against x

, but with

the linear trend with respect to x

added back into the plot. To examine the

relationship between the response y and a particular covariate x

deﬁne the

partial residuals as

= r +

. (3.4)

The partial residual plot is a plot of u

against x

.(Hereu

and x

are

variables with n values, and the subscript i has been suppressed.) The partial

residual plot shows much the same information as the ordinary residual plot

versus x

but, by showing the linear trend on the same plot, the partial

residual plots allows the analyst to judge the relative importance of any

linearity relative to the magnitude of the linear trend. When plotting residuals

versus x

, the focus is on existence of any nonlinear trends. With the partial

residual plot, the focus is on the relative importance of any nonlinearity in

the context of the linear trend.

3.5 Residual Plots 103

A partial residual plot can be seen as an attempt to achieve the same

eﬀect and simplicity of interpretation as the plot of y against x in simple

linear regression, but in the context of multiple regression. With multiple

predictors, plots of y against each explanatory variable are generally diﬃcult

to interpret because of the competing eﬀects of the multiple variables. The

partial residual plot shows the contribution of x

after adjusting for the other

variables currently in the model. The slope of a least-squares line ﬁtted to the

partial residual plot gives the coeﬃcient for that explanatory variable in the

full regression model. However, the variability of points around the line in the

partial residual plot may suggest to the eye that σ

is somewhat smaller than

it actually is, because the residuals being plotted are from the full regression

model with n − p



residual degrees of freedom, rather than from a simple

linear regression with n − 2 degrees of freedom.

Example 3.4. Consider the lungcap data again. Figure 1.1 (p. 6) shows the

relationships between fev and each explanatory variable without adjusting

for the other explanatory variables. The partial residuals can be computed

using resid():

> partial.resid <- resid( LC.lm, type="partial")

> head(partial.resid)

Ht Gender Smoke

1 -1.4958086 0.4026274 0.46481270

2 -1.7288086 -0.0897584 -0.02757306

3 -1.4658086 0.1732416 0.23542694

4 -1.1788086 0.4602416 0.52242694

5 -0.9908086 0.5185487 0.58073406

6 -1.1498086 0.3595487 0.42173406

The easiest way to produce the partial residual plots (Fig. 3.3)istouse

termplot(). We do so here to produce the partial residuals plot for Ht only

(Fig. 3.3):

> termplot( LC.lm, partial.resid=TRUE, terms="Ht", las=1)

termplot() also shows the ideal linear relationship in the plots. The partial

residual plot for Ht shows non-linearity, again suggesting the use of μ =

E[log(fev)] as the response variable.

The relationship between FEV and Ht appears quite strong after adjusting

for the other explanatory variables. Note that the slope of the simple regres-

sion line is equal to the coeﬃcient in the full model. For example, compare

the regression coeﬃcients for Ht:

> coef( summary(LC.lm) )

Estimate Std. Error t value Pr(>|t|)

(Intercept) -5.36207814 0.186552603 -28.7429822 7.069632e-118

Ht 0.12969288 0.003105995 41.7556591 3.739216e-186

GenderM 0.12764341 0.034093423 3.7439305 1.972214e-04

SmokeSmoker 0.03413801 0.058581034 0.5827485 5.602647e-01

104 3 Linear Regression Models: Diagnostics and Model-Building

45 50 55 60 65 70 75

−2

−1

Partial for Ht

Fig. 3.3 Partial residual plot Ht in the model LC.lm ﬁtted to the lung capacity data

(Example 3.4)

> lm.Ht <- lm( partial.resid[, 1]~lungcap$Ht)

> coef( summary(lm.Ht) )

Estimate Std. Error t value Pr(>|t|)

(Intercept) -7.9298868 0.179532816 -44.16957 3.629602e-198

lungcap$Ht 0.1296929 0.002923577 44.36102 4.369629e-199

The coeﬃcients for Ht are exactly the same. The full regression gives larger

standard errors than the simple linear regression however, because the latter

over-estimates the residual degrees of freedom. 

3.5.3 Plot Residuals Against ˆμ: Constant Variance

Plotting the residuals against ˆμ is primarily used to check for constant vari-

ance (Fig. 3.4). An increasing or decreasing trend in the variability of the

residuals about the zero line suggests the need to transform or change the

scale of the response variable to achieve constant variance. For example, if

the response variable is a positive quantity, and the plot of residuals versus ˆμ

shows an increasing spread of the residuals for larger ﬁtted values, this would

suggest a need to transform the response variable to compress the larger val-

ues, by taking logarithms or similar. Standardized residuals r



(rather than

the raw residuals r) are preferred in these plots, as standardized residuals

have approximately constant variance if the model ﬁts well.

Example 3.5. Returning to the lung capacity data, Fig. 3.5 shows that the

plot of residuals against ﬁtted values has a variance that is not constant,

but is increasing as the mean increases. In other words, there appears to be

an increasing mean–variance relationship. The plot also shows non-linearity,

again suggesting that the model can be improved:

3.5 Residual Plots 105

−0.10 0.00 0.10

−2

−1

Ideal plot: no pattern

Fitted values μ

Std Residuals r

012345

−2

−1

Non−linearity

Fitted values μ

Std Residuals r '

1234

−3

−2

−1

Non−constant variance

Fitted values μ

Std Residuals

r '

Fig. 3.4 Some example plots of the standardized residuals r



plotted against the ﬁtted

values ˆμ. The eﬀects are exaggerated from what is usually seen in practice (Sect. 3.5.1)

1234

−4

−2

Fitted values

Standardized residuals

Fig. 3.5 Standardized residual plotted against the ﬁtted values for the model LC.lm

ﬁtted to the lung capacity data (Example 3.5)

> # Plot std residuals against the fitted values

> scatter.smooth( rstandard( LC.lm ) ~ fitted( LC.lm ), col="grey",

las=1, ylab="Standardized residuals", xlab="Fitted values")



3.5.4 Q–Q Plots and Normality

The assumption of normality can be checked using a normal quantile–quantile

plot, or normal Q–Q plot, of the residuals. A Q–Q plot, in general, graphs

the quantiles of the data against the quantiles of given distribution; a normal

Q–Q plot graphs the quantiles of the data against the quantiles of a standard

normal distribution. For example, the value below which 30% of the data lie is

plotted against the value below which 30% of a standard normal distribution

lies. If the residuals have a normal distribution, the points will lie on a straight

106 3 Linear Regression Models: Diagnostics and Model-Building

line in the Q–Q plot. For this reason, a straight line is often added to the

Q–Q plot to assist in assessing normality. For small sample sizes, Q–Q plots

may be hard to assess (Problem 3.5).

Non-normality may appear as positive skewness (which is quite common);

negative skewness; as having too many observations in the tails of the dis-

tribution; or as having too few observations in the tails of the distribution

(Fig. 3.6). Q–Q plots are also a convenient way to check for the presence of

large residuals (Sect. 3.6.2). Since standardized residuals r



are more normally

distributed than raw residuals, Q–Q plots are more appropriate and outliers

are easier to identify using standardized residuals.

In r, Q–Q plots of residuals can be produced from a ﬁtted model fit

using qqnorm(), using either resid(fit) or rstandard(fit) as the input.

A reference line for assessing normality of the points is added by following the

qqnorm() command with the corresponding qqline() command, as shown

in the following example.

Example 3.6. Consider the lungcap data again (Example 1.1), and model

LC.lm ﬁtted to the data. The Q–Q plot (Fig. 3.7) suggests that the normality

assumption is suspect:

> # Q-Q probability plot

> qqnorm( rstandard( LC.lm ), las=1, pch=19)

> qqline( rstandard( LC.lm ) ) # Add reference line

The distribution of residuals appears to have heavier tails than the normal

distribution in both directions, because the residuals curve above the line

on the right and below the line on the left. The plot also shows a number

of large residuals, both positive and negative, suggesting the model can be

improved. 

3.5.5 Lag Plots and Dependence over Time

Dependence is not always easy to detect, if not already obvious from the data

collection process. When data are collected over time, dependence between

successive response can be detected by plotting each residual against the

previous residual in time, often called the lagged residual. If the responses are

independent, the plots should show no pattern under (Fig. 3.8, left panel).

−2 −1 0 1 2

Right skewed

Theoretical Quantiles

Sample Quantiles

−2 −1 0 1 2

Left skewed

Theoretical Quantiles

Sample Quantiles

−2 −1 0 1 2

Tails too light

Theoretical Quantiles

Sample Quantiles

Right skewed

Residuals

Frequency

0246810

Left skewed

Residuals

Frequency

0246810

Tails too light

Residuals

Frequency

0246810

−2 −1 0 1 2

Tails too heavy

Theoretical Quantiles

Sample Quantiles

−2 −1 0 1 2

Bimodal distribution

Theoretical Quantiles

Sample Quantiles

−2 −1 0 1 2

True normal distribution

Theoretical Quantiles

Sample Quantiles

Tails too heavy

Residuals

Frequency

0246810

Bimodal distribution

Residuals

Frequency

0246810

True normal distribution

Residuals

Frequency

0246810

Fig. 3.6 Typical Q–Q plots of standardized residuals. In all cases, the sample size is

150. The solid line is added as a reference to aid is assessing linearity of the points

(Sect. 3.5.4)

108 3 Linear Regression Models: Diagnostics and Model-Building

−3 −2 −1 0 1 2 3

−4

−2

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

Fig. 3.7 The Q–Q plot for model LC.lm ﬁtted to the lung capacity data (Example 3.6)

−3

−2

−1

−3

−2

−1

Independent residuals

t−1

−3

−2

−1

−3

−2

−1

Negatively correlated

residuals

t−1

−3

−2

−1

−3

−2

−1

Positively correlated

residuals

t−1

Fig. 3.8 Some example plots of the residuals at time t, denoted r

, plotted against the

previous residual in time r

t−1

(Sect. 3.5.5)

3.6 Outliers and Inﬂuential Observations

3.6.1 Introduction

The previous section presented tools for assessing overall model assumptions.

This section discusses methods for detecting problems with individual obser-

vations. The two issues may be related: an incorrect model speciﬁcation may

indicate problems with a particular observation. Consequently, the methods

in Sect. 3.5 should be used in conjunction with the methods in this section.

3.6 Outliers and Inﬂuential Observations 109

3.6.2 Outliers and Studentized Residuals

Outliers are observations inconsistent with the rest of the data set. Incon-

sistent observations are located by identifying the corresponding residual as

unusually large (positive or negative). This may be done by using Q–Q plots

or other plots already produced for assessing the model assumptions. As a

guideline, potential outliers might be ﬂagged as observations with standard-

ized residual r



greater than, say, 2.5 in absolute value. This is naturally only

a guideline to guide further investigation, as approximately 1.2% of observa-

tions will have absolute standardized residuals exceeding 2.5 just by chance

even when there are no outliers and all the model assumptions are correct.

Standardized residuals are computed using s

, which is computed from

the entire data set. An observation with a large raw residual is actually used

to compute s

and perhaps inﬂating its value, in turn making the unusual

observation hard to detect. This suggests omitting Observation i from the cal-

culation of s

when computing the residual for Observation i. These residuals

are called Studentized residuals.

To ﬁnd the Studentized residual r



, ﬁrst ﬁt a linear regression model to

all the data except case i. Then compute the estimate of the variance s

(i)

from this model based on the remaining n −1 observations, the subscript (i)

indicating that Observation i has been omitted in computing the estimate.

Then, the Studentized residuals are



√

− ˆμ

i(i)

)

(i)

√

1 − h

, (3.5)

where ˆμ

i(i)

is the ﬁtted value for Observation i computed from the model

ﬁtted without Observation i. This deﬁnition appears to be cumbersome to

compute, since computing r



for all n observations apparently requires ﬁtting

n+1 models (the original with all observations, plus a model when each obser-

vation is omitted). However, numerical identities are available for computing



without the need for repeated linear regressions. Using r, Studentized

residuals are easily found using rstudent().

Example 3.7. For the lungcap data, the residual plot in Fig. 3.2 (p. 102)

shows no outliers (but does shows some large residuals, both positive and

negative), so r



and r



are expected to be similar:

> summary( cbind( Standardized = rstandard(LC.lm),

Studentized = rstudent(LC.lm) ) )

Standardized Studentized

Min. :-3.922299 Min. :-3.966502

1st Qu.:-0.596599 1st Qu.:-0.596304

Median : 0.002062 Median : 0.002061

Mean : 0.000213 Mean : 0.000387

3rd Qu.: 0.559121 3rd Qu.: 0.558826

Max. : 4.885392 Max. : 4.973802



110 3 Linear Regression Models: Diagnostics and Model-Building

Example 3.8. For the model LC.lm ﬁtted to the lungcap data in Example 3.1,

the Studentized residuals can be computed by manually deleting each ob-

servation. For example, deleting Observation 1 and reﬁtting produces the

Studentized residual for Observation 1:

> # Fit the model *without* Observation 1:

> LC.no1 <- lm( FEV ~ Ht + Gender + Smoke,

data=lungcap[-1,]) # The negative index *removes* row 1

> # The fitted value for Observation 1, from the original model:

> mu <- fitted( LC.lm )[1]

> # The estimate of s from the new model, without Obs. 1:

> s <- summary(LC.no1)$sigma

> h <- hatvalues( LC.lm )[1] # Hat value, for Observation 1

> resid.stud <- ( lungcap$FEV[1] - mu ) /(s*sqrt(1-h) )

> resid.stud

1.104565

> rstudent(LC.lm)[1] # The easy way

1.104565



3.6.3 Inﬂuential Observations

Inﬂuential observations are observations that substantially change the ﬁtted

model when omitted from the data set. Inﬂuential observations necessarily

have moderate to large residuals, but are not necessarily outliers. Similarly,

outliers may or may not be inﬂuential.

More speciﬁcally, inﬂuential observations are those that combine large

residuals with high leverage (Fig. 3.9). That is, inﬂuential observations are

outliers with high leverage. A popular measure of inﬂuence for observation i

is Cook’s distance:

D =



)





1 − h



. (3.6)

(The subscript i has been omitted here from all quantities for brevity.)

Problem 3.4 develops another interpretation. The values of Cook’s distance

are found in r using cooks.distance().

Approximately, D has an F -distribution with (p



,n− p



) degrees of free-

dom [9], so a conservative approach for identifying inﬂuential observations

uses the 50th percentile point of the F -distribution as a guideline [39]. This

guideline is used by r. For most F -distributions, the 50th percentile is near

1, so a useful rule-of-thumb is that observations with D>1 may be ﬂagged

as potentially inﬂuential. Other guidelines also exist for identifying high-

inﬂuence outliers [10, 12].

3.6 Outliers and Inﬂuential Observations 111

Outlier with high influence

Outlier with low influence

No outliers; no high

influence observations

Fig. 3.9 Three examples showing the relationship between outliers and inﬂuential ob-

servations. The solid circle is the outlier, the solid line is the regression line including

the outlier; the dashed line is the regression line omitting the outlier (Sect. 3.6.3)

Another measure of the inﬂuence of Observation i, very similar to Cook’s

distance, is dffits. dffits measures how much the ﬁtted value of Obser-

vation i changes between the model ﬁtted with all the data and the model

ﬁtted when Observation i is omitted:

dffits

ˆμ

− ˆμ

i(i)

(i)

= r





1 − h

where ˆμ

i(i)

is the estimate of μ

from the model ﬁtted after omitting Obser-

vation i from the data. dffits

is essentially equivalent to the square root of

Cook’s distance. dffits

diﬀers from Cook’s distance only by a factor of 1/p



and by replacing s

with s

(i)

. dffits are computed in r using dffits().

dfbeta is a coeﬃcient-speciﬁc version of dffits, which measures how

much the estimates of each individual regression coeﬃcient change between

the model ﬁtted using all observations and the model ﬁtted with Observation i

omitted:

dfbetas

−

j(i)

se(

j(i)

)

where

j(i)

is the estimate of β

after omitting Observation i and se(

j(i)

)is

the standard error of

using s

(i)

to estimate the error standard deviation.

One set of dfbetas is produced for each model coeﬃcient. The dfbetas are

computed in r using dfbetas().

Yet another measure of inﬂuence, the covariance ratio (cr), measures the

increase in uncertainty about the regression coeﬃcients when Observation i

is omitted. Mathematically, cr is the ratio by which the volume of the con-

ﬁdence ellipsoid for the coeﬃcient vector increases when Observation i is

112 3 Linear Regression Models: Diagnostics and Model-Building

omitted. More simply, the square root of cr can be interpreted as the av-

erage factor by which the conﬁdence intervals for the regression coeﬃcients

become wider when Observation i is omitted. A convenient computational

formula for cr is:

cr =

1 − h



n − p



+(r



)



where r



is the Studentized residual (3.5). In r, the function covratio()

computes cr.

The r function influence.measures() produces a table of the inﬂuence

measures dfbetas, dffits, cr and D, plus the leverages h. Observations

identiﬁed as inﬂuential with respect to any of these statistics (or having high

leverage in the case of h) are ﬂagged with a * according to the following

criteria:

• dfbetas: Observation i is declared inﬂuential when |dfbetas

| > 1.

• dffits: Observation i is declared inﬂuential when

|dffits

| > 3/





/(n − p



• Covariance ratio cr: Observation i is declared inﬂuential when cr



/(n − p



• Cook’s distance D: Observation i is declared inﬂuential when D exceeds

the 50th percentile of the F distribution with (p



,n−p



) degrees of free-

dom.

• Leverages h: Observations are declared high leverage if h>3p



/n.

Diﬀerent observations may be declared as inﬂuential by the diﬀerent criteria.

The covariance ratio has a tendency to declare more observations as inﬂuen-

tial than the other criteria.

Example 3.9. Consider the lung capacity data again (Example 1.1; data set:

lungcap), and model LC.lm (Example 3.1,p.97). The observations with the

smallest and largest values of Cook’s distance are:

> cd.max <- which.max( cooks.distance(LC.lm)) # Largest D

> cd.min <- which.min( cooks.distance(LC.lm)) # Smallest D

> c(Min.Cook = cd.min, Max.Cook = cd.max)

Min.Cook.69 Max.Cook.613

69 613

The values of dffits, cv and Cook’s distance for these observations can be

found as follows:

> out <- cbind( DFFITS=dffits(LC.lm),

Cooks.distance=cooks.distance(LC.lm),

Cov.ratio=covratio(LC.lm))

3.6 Outliers and Inﬂuential Observations 113

These statistics for the observations cd.max and cd.min are:

> round( out[c(cd.min, cd.max),], 5) # Show the values for these obs only

DFFITS Cooks.distance Cov.ratio

69 0.00006 0.00000 1.01190

613 -0.39647 0.03881 0.96737

From these three measures, Observation 613 is more inﬂuential than Observa-

tion 69 according to dffits and Cook’s distance (but not cv). Now examine

inﬂuence of Observation 613 and 69 on each of the regression parameters:

> dfbetas(LC.lm)[cd.min,] # Show DBETAS for cd.min

(Intercept) Ht GenderM SmokeSmoker

4.590976e-05 -3.974922e-05 -2.646158e-05 -1.041249e-06

> dfbetas(LC.lm)[cd.max,] # Show DBETAS for cd.max

(Intercept) Ht GenderM SmokeSmoker

0.05430730 -0.06394615 0.10630441 -0.31682958

Omitting Observation 69 (cd.min) makes almost no diﬀerence to the re-

gression coeﬃcients. Observation 613 is clearly more inﬂuential than Obser-

vation 69, as expected. The r function influence.measures() is used to

identify potentially inﬂuential observations according to r’s criteria:

> LC.im <- influence.measures( LC.lm ); names(LC.im)

[1] "infmat" "is.inf" "call"

The object LC.im contains the inﬂuence statistics (as LC.im$infmat), and

whether or not they are inﬂuential according to r’s criteria (LC.im$is.inf):

> head( round(LC.im$infmat, 3) ) # Show for first few observations only

dfb.1_ dfb.Ht dfb.GndM dfb.SmkS dffit cov.r cook.d hat

1 0.117 -0.109 -0.024 0.015 0.127 1.012 0.004 0.013

2 -0.005 0.005 0.001 -0.001 -0.006 1.017 0.000 0.010

3 0.051 -0.047 -0.014 0.005 0.058 1.015 0.001 0.010

4 0.113 -0.104 -0.031 0.012 0.127 1.007 0.004 0.010

5 0.116 -0.106 -0.036 0.010 0.133 1.004 0.004 0.009

6 0.084 -0.077 -0.026 0.007 0.097 1.009 0.002 0.009

> head( LC.im$is.inf )

dfb.1_ dfb.Ht dfb.GndM dfb.SmkS dffit cov.r cook.d hat

1 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

2 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

3 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

4 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

5 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

6 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

To determine how many entries in the columns of LC.im$is.inf are TRUE,

sum over the columns (this works because r treats FALSE as 0 and TRUE as 1):

> colSums( LC.im$is.inf )

dfb.1_ dfb.Ht dfb.GndM dfb.SmkS dffit cov.r cook.d hat

0000185607

114 3 Linear Regression Models: Diagnostics and Model-Building

Seven observations have high leverage, as identiﬁed by the column labelled

hat, 56 observations are identiﬁed by the covariance ratio as inﬂuential, but

Cook’s distance does not identify any observation as inﬂuential.

We can also determine how many criteria declare observations as inﬂuential

by summing the relevant columns of LC.im$is.inf over the rows:

> table( rowSums( LC.im$is.inf[, -8] ) ) # Omitting leverages (col 8)

012

590 54 10

This shows that most observations are not declared inﬂuential on any of the

criteria, and 54 observations declared as inﬂuential on just one criterion.

For Observations 69 and 613 explicitly:

> LC.im$is.inf[c(cd.min, cd.max), ]

dfb.1_ dfb.Ht dfb.GndM dfb.SmkS dffit cov.r cook.d hat

69 FALSE FALSE FALSE FALSE FALSE FALSE FALSE FALSE

613 FALSE FALSE FALSE FALSE TRUE TRUE FALSE FALSE

Observation 613 is signiﬁcantly inﬂuential based on dffits and cv.

A plot of these inﬂuence diagnostics is often useful (Fig. 3.10), using type=

"h" to draw histogram-like (or high-density) plots:

> # Cooks' Distance

> plot( cooks.distance( LC.lm ), type="h", main="Cook's distance",

ylab="D", xlab="Observation number", las=1 )

> # DFFITS

> plot( dffits( LC.lm ), type="h", main="DFFITS",

ylab="DFFITS", xlab="Observation number", las=1 )

0 200 500

0.00

0.01

0.02

0.03

0.04

Cook's distance

Observation number

0 200 500

−0.4

−0.2

0.0

0.2

0.4

DFFITS

Observation number

DFFITS

0 200 500

−0.10

−0.05

0.00

0.05

0.10

0.15

0.20

DFBETAS for beta2

Observation number

DFBETAS

Fig. 3.10 Inﬂuence diagnostics for model LC.lm ﬁtted to the lung capacity data. Left

panel: Cook’s distance D

; centre panel: dffits; right panel: dfbetas for β

(Exam-

ple 3.9)

3.8 Remedies: Fixing Identiﬁed Problems 115

> # DFBETAS for beta_2 only (that is, column 3)

> dfbi <- 2

> plot( dfbetas( LC.lm )[, dfbi + 1], type="h", main="DFBETAS for beta2",

ylab="DFBETAS", xlab="Observation number", las=1 )



3.7 Terminology for Residuals

The terminology used for residuals is confusingly inconsistent. Generally in

statistics, dividing some quantity by an estimate of its standard deviation

is called standardizing. More speciﬁcally, dividing a quantity which follows a

normal distribution by the sample standard deviation to produce a quantity

which follows a t-distribution is called Studentizing, following the approach

used by Student [37] when introducing the t-distribution.

Under these commonly-used deﬁnitions, both r



and r



are standardized

and Studentized residuals, and various authors use the terms for describing

both residuals. Following r and Belsley et al. [3], we call r



the Studen-

tized residual (Sect. 3.6.2; rstudent() in r) because it follows a Student’s

t-distribution exactly, whereas r



will simply be called the standardized resid-

ual (Sect. 3.3; rstandard() in r).

An alternative convention [39] is to call r



the internally Studentized resid-

ual and r



the externally Studentized residual. These labels are perhaps more

speciﬁc and descriptive of the diﬀerences between the two types of residuals,

but have not become widely used in the literature.

3.8 Remedies: Fixing Identiﬁed Problems

The past few sections have described a variety of diagnostics for identifying

diﬀerent types of weaknesses in the ﬁtted model. The next few sections will

consider some standard strategies for modifying the ﬁtted model in order to

remedy or ameliorate speciﬁc problems.

One commonly-occurring problem is that the response is recorded on a

measurement scale for which the variance increases or decreases with the

mean. If this is the case, the variance can often be stabilized by transforming

the response to a diﬀerent scale (Sect. 3.9).

Sometimes a nonlinear relationship between y and x canbeﬁxedbya

simple transformation of x (Sect. 3.10). More generally, a complex relation-

ship between a covariate and the response signals the need to build further

terms into the model to capture this relationship (Sections 3.11 and 3.12).

Usually the measurement scale of y should be settled before transforming

116 3 Linear Regression Models: Diagnostics and Model-Building

the covariates, because any transformation of y will obviously impact on the

shape of its relationships with the covariates.

Often the above steps will solve structural problems and hence also tend

to reduce the number of apparent outliers or dangerously inﬂuential observa-

tions. If some remain, however, decisions must be made to remove the out-

liers or to accommodate them into a modiﬁed model. Section 3.13 discusses

these issues.

One possible problem that will not be discussed in detail later is that

of correlated residuals. Dependence between responses can arise from com-

mon causes shared between observations, or from a carryover eﬀect from

one observation to another, or from other causes. When the responses fail

to be independent, there are a variety of more complex models that can

be developed to accommodate this dependence, including generalized least

squares [8], mixed models [40] or spatial models [5]. All of these possibilities

however would take us outside the scope of this book.

3.9 Transforming the Response

3.9.1 Symmetry, Constraints and the Ladder of

Powers

The idea of a transformation is to convert the response variable to a diﬀerent

measurement scale. For example, consider the acidity of swimming pool wa-

ter. From a chemical point of view, acidity is measured by the concentration

of hydrogen ions. However acidity is more commonly expressed in terms of

pH-level. If y is hydrogen ion concentration, then the pH level is deﬁned by

pH= −log

y. This serves as an alternative and, for many purposes, more

useful scale on which to measure the same quantity. In mathematical terms,

a new response variable y

∗

= h(y) is computed from y, where h() is some

invertible function, and then a linear regression model is built for y

∗

instead

of y. In the case of the pH-level, h(y)=−log

y. After transforming the

response, the basic linear regression model structure remains the same, the

new variable y

∗

simply replacing y. The model becomes



∗

∼ N(μ

,σ

)

= β



j=1

(3.7)

Note that now μ

=E[y

∗

] rather than E[y

]. After transforming the response,

one will typically reﬁt the model and produce new residual plots to recheck

assumptions for the new model. This may be done iteratively until a satis-

factory transformation is found.

There are three main reasons why one might choose to transform the re-

sponse variable. First, transforming the measurement scale so that it covers

3.9 Transforming the Response 117

the whole real line can avoid diﬃculties with constraints on the linear regres-

sion coeﬃcients. In the lung capacity study, for example, ideally we would

like to ensure that our model will never predict a negative value for fev.The

diﬃculty with predicting negative values for fev can be avoiding by building

a linear regression model for y

∗

= log(fev) instead of for fev itself, because

any predicted value for the logarithm of fev, whether negative or positive,

translates into a positive value for fev itself.

When y is a count for which zero is a possible value, the starred log-

transformations y

∗

= log (y +0.5) or y

∗

= log (y + 1) have been used to

avoid taking the logarithm of zero. When y is a count out of a possible total

n, then the empirical logistic transformation y

∗

= log{(y +0.5)/(n+0.5)} has

sometimes been used. In both cases the motivation is the same: to convert

the response to a scale for which the linear predictor is unconstrained. These

transformations can be successful if the counts are not too small or too near

the boundary values.

A second possible reason for transforming the response is to cause its

distribution to be more nearly normally distributed. Typically this means

trying to make the distribution of y-values more symmetric. For example,

consider the acidity of swimming pool water again. The concentration of

hydrogen ions is a strictly positive quantity, usually very close to zero but

varying by orders of magnitude from one circumstance to another. Hence

hydrogen concentration is likely have a highly right-skewed distribution. By

contrast, the pH-levels are usually more symmetrically distributed. In other

words, the pH-level is likely to be more nearly normally distributed than

is the hydrogen ion concentration itself. Right skew distributions arise most

commonly when the response measures a physical quantity that can only take

positive values. In such a case, a log-transformation, y

∗

= log y, or a power

transformation, y

∗

= y

with λ<1, will reduce the right skewness. Common

values for λ make up what is sometimes called a ladder of powers (Table 3.1).

The smaller λ is chosen, the stronger the transformation. A too small value

for λ will reverse a right skew distribution to one that is left skew. The usual

procedure is to start with a transformation with λ near one, then decrease λ

until symmetry of the residuals from the regression is roughly achieved.

If y is left skewed, then a power transformation y

∗

= y

with λ>1 might

be used (Table 3.1). Such situations are less common however.

3.9.2 Variance-Stabilizing Transformations

There is a third and even more fundamental motivation for transforming

the response variable, which is to try to achieve close to constant variance

across all observations. Again we focus on the commonly-occurring situation

in which y measures some physical quantity that can only take on positive

values. For such a variable, it is almost inevitable that the variance of y

will be smaller when μ is close to zero than when μ is large, because of

118 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3 .1 The ‘ladder of powers’. Variance increasing with mean is more common than

variance decreasing with the mean, hence the transformations on the right-hand side

are more commonly used. Note that λ = 1 produces no transformation of the response

(Sect. 3.9)

Transformation: ← ... y

√

y log y 1/

√

y 1/y 1/y

···→

Box–Cox λ: ← ... 32 11/20−1/2 −1 −2 ···→

Primary use: • When variance • When variance increases with

decreases with increasing mean

increasing mean

Other uses: • When y left-skewed • When y right-skewed

the requirement that the range of y is restricted to positive values. This

phenomenon will become readily apparent in practical terms when the values

of y vary by orders of magnitude in a single data set. In these cases, we say

that y shows a positive mean–variance relationship.

In the scientiﬁc literature, the uncertainty of physical measurements of

positive quantities are often expressed in terms of the coeﬃcient of variation

(standard deviation divided by the mean) instead of in terms of variance or

standard deviation. This is because the coeﬃcient of variation often tends to

be more nearly constant across cases than is the standard deviation, so it is

more useful to express variability in relative terms rather than in absolute

terms. Mathematically, this means that the standard deviation σ of y is

proportional to the mean μ or, equivalently, the variance is proportional

to the mean squared, var[y]=φμ

for some φ. In such cases, y is said to

have a quadratic mean–variance relationship. The strongest motivation for

transforming the response is usually to try to remove the mean–variance

relationship.

If y takes positive values, then the ladder of powers may be used to remove

or mitigate a mean–variance relationship (Table 3.1). A power transformation

with λ<1 will reduce or remove an increasing mean–variance relationship,

while λ>1 will reduce or remove a decreasing mean–variance relationship.

More generally, we consider the class of variance-stabilizing transforma-

tions. Suppose that y has a mean–variance relationship deﬁned by the func-

tion V (μ), with var[y]=φV (μ). Then, consider a transformation y

∗

= h(y).

A ﬁrst-order Taylor series expansion of h(y)aboutμ gives y

∗

= h(y) ≈

h(μ)+h



(μ)(y −μ), from which it can be inferred that

var[y

∗

]=var[h(y)] ≈ h



(μ)

var[y].

Hence the transformation y

∗

= h(y) will approximately stabilize the variance

if h



(μ) is proportional to var[y]

−1/2

= V (μ)

−1/2

. When V (μ)=μ

(standard

deviation proportional to the mean), the variance-stabilizing transformation

is the logarithm, because then h



(μ)=1/μ. When V (μ)=μ, the variance-

stabilizing transformation is the square root, because h



(μ)=1/μ

1/2

3.9 Transforming the Response 119

The most common variance-stabilizing transformations appear on a ladder

of powers (Table 3.1). To use this ladder, note that the milder transformations

are closer to λ = 1 (no transformation). It is usual to start with mild transfor-

mations and progressively try more severe transformations as necessary. For

example, if a logarithmic transformation still produces increasing variance as

the mean increases, try the next transformation on the ladder: 1/

√

y.The

most commonly-used transformation is the logarithmic transformation.

When y is a proportion or percentage (taking values from zero to one, or

zero to 100%), the mean–variance relationship is likely to be unimodal. In

such cases, the possible values for y have two boundaries, one at zero and

the other at one, and the variance of y is likely to decrease as the mean ap-

proaches either boundary. Proportions often show a quadratic mean–variance

relationship of the form V (μ) ∝ μ(1 − μ), with 0 <μ<1. In such cases, the

variance-stabilizing transformation is the arc-sin–square root transformation

∗

=sin

−1

√

Transformations with λ ≤ 0 can only be applied to positive values of y.If

negative values are present, then power transformations should not be used.

If y is positive except for a few exact zeros, one has the choice between using a

positive value of λ, for example a small positive value such as λ =1/4 instead

of a log-transformation, or else oﬀsetting y to be positive before transforming.

For example, a response variable such as rainfall is positive and continuous

on days when rain has occurred, but is zero otherwise. In such cases, the

starred logarithmic transformation, y

∗

= log(y +c) where c is a small positive

constant, has sometimes been used. Such transformations should be used with

caution, as they are sensitive to the choice of oﬀset c. Choosing c too small

can easily introduce outliers into the data.

Example 3.10. For the lungcap data, we have established that the model LC.

lm is inadequate (Example 3.3). For example, a plot of r



against ˆμ

(Fig. 3.5)

shows non-constant variance. Various transformations of the response can be

used to determine which, if any, transformation of the response is appropriate

(Fig. 3.11). Since the variance increases with increasing mean, try the ﬁrst

transformation suggested on the ladder of powers (Table 3.1,p.118), the

square root transformation:

> LC.sqrt <- update( LC.lm, sqrt(FEV) ~ .)

> scatter.smooth( rstandard(LC.sqrt)~fitted(LC.sqrt), las=1, col="grey",

ylab="Standardized residuals", xlab="Fitted values",

main="Square-root transformation")

This transformation (Fig. 3.11, top right panel) produces slightly increasing

variance. Try the next transformation on the ladder, the commonly-used

logarithmic transformation:

> LC.log <- update( LC.lm, log(FEV) ~ .)

> scatter.smooth( rstandard(LC.log)~fitted(LC.log), las=1, col="grey",

ylab="Standardized residuals", xlab="Fitted values",

main="Log transformation")

120 3 Linear Regression Models: Diagnostics and Model-Building

1234

−4

−2

No transformation

Fitted values

Standardized residuals

1.0 1.4 1.8

−4

−2

Square−root transformation

Fitted values

Standardized residuals

0.5 1.0 1.5

−4

−2

Log transformation

Fitted values

Standardized residuals

−0.2 0.0 0.1 0.2

−895

−885

log−Likelihood

95%

Fig. 3.11 Transformations of the fev in the data frame lungcap. The original data

(top left panel); using a square root transformation (top right panel); using a logarithmic

transformation (bottom left panel); a plot to ﬁnd the Box–Cox transformation (bottom

right panel) (Examples 3.10 and 3.11)

This plot show approximately constant variance and no trend. The logarith-

mic transformation appears suitable, and also allows easier interpretations

than using the square root transformation. A logarithmic transformation of

the response is required to produce almost constant variance, as used in

Chap 2. 

3.9.3 Box–Cox Transformations

Notice that the transformations in Table 3.1 have the form of y raised to some

power, except for the logarithmic transformation. The logarithmic transfor-

mation also ﬁts the general power-transformation form if we deﬁne

∗

⎧

⎨

⎩

− 1

for λ =0

log y for λ =0.

(3.8)

3.10 Simple Transformations of Covariates 121

This family of transformations is called the Box–Cox transformation [7]. The

form of the Box–Cox transformation (3.8) is continuous in λ when natural

logarithms are used, since (y

−1)/λ → log y as λ → 0. The Box–Cox trans-

formation (3.8) has the same impact as the transformation y

∗

= y

, but the

results diﬀer numerically. For example, λ = 1 transforms the responses y to

(y−1), which has no impact on the model structure, but the numerical values

of the response change.

Computationally, various values of λ are chosen, and the transformation

producing the response y

∗

with approximately constant variance is then cho-

sen. This approach can be implemented in r directly, or by using the function

boxcox() (in the package MASS). The boxcox() function uses the maximum

likelihood criterion, discussed in the next chapter of this book. It ﬁnds the

optimal λ to achieve linearity, normality and constant variance simultane-

ously.

Example 3.11. Continuing using the lungcap data from the previous exam-

ple, we use the boxcox() function to estimate the optimal Box–Cox trans-

formation. In the plot produced, higher log-likelihood values are preferable.

The maximum of the Box–Cox plot is achieved when λ is just above zero,

conﬁrming that a logarithmic transformation is close to optimal for achieving

linearity, normality and constant variance (Fig. 3.11, bottom right panel):

> library(MASS) # The function boxcox() is in the MASS package

> boxcox( FEV ~ Ht + Gender + Smoke,

lambda=seq(-0.25, 0.25, length=11), data=lungcap)



3.10 Simple Transformations of Covariates

Sometimes, to achieve linearity or to reduce the inﬂuence of inﬂuential ob-

servations, transformations of the covariates are required (Fig. 3.12). Using

transformed covariates still produces a model linear in the parameters. Trans-

formations may apply to any or all of the covariates. (Transforming factors

makes no sense.)

Example 3.12. The wind velocity and corresponding direct current (dc) out-

put from windmills (Table 3.2; data set: windmill) was recorded [18, 19].

A plot of the data (Fig. 3.13, left panels) shows non-linearity, but little ev-

idence of non-constant variance (so a transformation of the response is not

recommended):

> data(windmill); names(windmill)

[1] "Wind" "DC"

122 3 Linear Regression Models: Diagnostics and Model-Building

Fig. 3.12 Transformations of covariates to achieve linearity (Sect. 3.10)

Tabl e 3 .2 The dc output from windmills at various wind velocities (in miles/h)

(Example 3.2)

Wind velocity dc output Wind velocity dc output Wind velocity dc output

2.45 0.123 4.60 1.562 7.85 2.179

2.70 0.500 5.00 1.582 8.15 2.166

2.90 0.653 5.45 1.501 8.80 2.112

3.05 0.558 5.80 1.737 9.10 2.303

3.40 1.057 6.00 1.822 9.55 2.294

3.60 1.137 6.20 1.866 9.70 2.386

3.95 1.144 6.35 1.930 10.00 2.236

4.10 1.194 7.00 1.800 10.20 2.310

7.40 2.088

> scatter.smooth( windmill$DC ~ windmill$Wind, main="No transforms",

xlab="Wind speed", ylab="DC output", las=1)

> wm.m1 <- lm( DC ~ Wind, data=windmill )

> scatter.smooth( rstandard(wm.m1) ~ fitted(wm.m1), main="No transforms",

xlab="Standardized residulas", ylab="Fitted values", las=1)

To alleviate the non-linearity, we try some transformations of the wind-

speed. Based on Fig. 3.12, we initially try a logarithmic transformation of

Wind, the most common transformation (Fig. 3.13, centre panels):

> scatter.smooth( windmill$DC ~ log(windmill$Wind), main="Log(Wind)",

xlab="log(Wind speed)", ylab="DC output", las=1)

> wm.m2 <- lm( DC ~ log(Wind), data=windmill )

> scatter.smooth( rstandard(wm.m2) ~ fitted(wm.m2), main="Log(Wind)",

ylab="Standardized residuals", xlab="Fitted values", las=1)

3.10 Simple Transformations of Covariates 123

46810

0.5

1.0

1.5

2.0

No transforms

Wind speed

DC output

1.0 1.5 2.0 2.5

−2

−1

No transforms

Standardized residulas

Fitted values

1.0 1.4 1.8 2.2

0.5

1.0

1.5

2.0

Log(Wind)

log(Wind speed)

DC output

0.5 1.0 1.5 2.0 2.5

−2

−1

Log(Wind)

Fitted values

Standardized residuals

0.10 0.20 0.30 0.40

0.5

1.0

1.5

2.0

1/Wind

1/(Wind speed)

DC output

0.5 1.0 1.5 2.0

−2.0

−1.5

−1.0

−0.5

0.0

0.5

1.0

1/Wind

Fitted values

Standardized residuals

Fig. 3.13 The windmill data. Left panels: the original data; centre panels: using the

logarithm of Wind; right panels: using the inverse of Wind; top panels: DC against the

covariate or transformed covariate; bottom panels: the standardized residuals against

the covariate or transformed covariate (Example 3.12)

The relationship is still non-linear, so try a more extreme transformation,

such as a reciprocal transformation of Wind (Fig. 3.13, right panels):

> scatter.smooth( windmill$DC ~ (1/windmill$Wind), main="1/Wind",

xlab="1/(Wind speed)", ylab="DC output", las=1)

> wm.m3 <- lm( DC ~ I(1/Wind), data=windmill )

> scatter.smooth( rstandard(wm.m3) ~ fitted(wm.m3), main="1/Wind",

ylab="Standardized residuals", xlab="Fitted values", las=1)

Note the use of I() when using lm(). This is needed because 1/Wind has

a diﬀerent meaning in an r formula than what is intended here. The term

1/Wind would mean to ﬁt a model with Wind nested within the intercept, an

interpretation which makes no sense here. To tell r to interpret 1/Wind as

an arithmetic expression rather than as a formula we insulate it (or inhibit

interpretation as a formula operator) by surrounding it with the function

I(). (For another example using I(), see Example 3.15,p.128.)

The relationship is now approximately linear, and the variance is ap-

proximately constant. The diagnostics show the model is mostly adequate

(Fig. 3.14):

124 3 Linear Regression Models: Diagnostics and Model-Building

510152025

0.00

0.05

0.10

0.15

0.20

Index

Cook's distance D

−2 −1 0 1 2

−2.0

−1.5

−1.0

−0.5

0.0

0.5

1.0

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

Fig. 3.14 Diagnostic plots from ﬁtting a model with the inverse of Wind to the windmill

data. Left: Cook’s distance; right: the Q–Q plot of standardized residuals (Example 3.12)

> plot( cooks.distance( wm.m3 ), type="h", las=1, ylab="Cook's distance D")

> qqnorm( rstandard( wm.m3), las=1 ); qqline( rstandard( wm.m3 ), las=1 )

No observations appear inﬂuential; no standardized residuals appear large

(though the normality of the residuals may be a little suspect). The system-

atic component is

> coef( wm.m3 )

(Intercept) I(1/Wind)

2.978860 -6.934547



A special case where simultaneous log-transformations of both x and y can

be useful is that where physical quantities may be related through power laws.

If y is proportional to some power of x such that E[y]=αx

, the relationship

may be linearized by logging both x and y, since E[log y] ≈ log α + β log x.

Example 3.13. In the lung capacity study (data set: lungcap), fev is a vol-

ume measure and hence is in units of length cubed, whereas height is in

ordinary units of length. Other things being equal, one would expect volume

to be proportional to a length measure (like height) cubed. On the log-scale,

we would expect log(FEV) to be linearly related to log(Ht) with a slope close

to 3, and this turns out to be so (Fig. 3.15):

> LC.lm.log <- lm(log(FEV)~log(Ht), data=lungcap)

> printCoefmat(coef(summary(LC.lm.log)))

Estimate Std. Error t value Pr(>|t|)

(Intercept) -11.921103 0.255768 -46.609 < 2.2e-16 ***

log(Ht) 3.124178 0.062232 50.202 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

> plot( log(FEV) ~ log(Ht), data=lungcap, las=1)



3.10 Simple Transformations of Covariates 125

3.9 4.0 4.1 4.2 4.3

0.0

0.5

1.0

1.5

log(Ht)

log(FEV)

Fig. 3.15 The logarithm of fev plotted against the logarithm of height for the lung

capacity data (Example 3.13)

Example 3.14. The volume y (in cubic feet) of 31 black cherry trees was

measured [2, 28, 34] as well as the height (in feet) and the girth, or diameter,

at breast height (in inches) (Table 3.3; data set: trees):

> data(trees) # The trees data frame comes with R

> plot( Volume ~ Height, data=trees, las=1, pch=19, xlab="Height (feet)",

ylab="Volume (cubic feet)", main="Volume vs height", las=1)

> plot(Volume ~ Girth, data=trees, las=1, pch=19, xlab="Girth (inches)",

ylab="Volume (cubic feet)", main="Volume vs girth", las=1)

The volume of the tree is related to the volume of timber, which is im-

portant economically. The relationships between the tree volume and height,

and tree volume and girth, both appear non-linear (Fig. 3.16, top panels).

An appropriate systematic component can be developed by approximat-

ing the cherry trees as either cones or cylinders in shape. For these shapes,

formulae for computing the timber volume y in cubic feet from the height

in feet h and the girth (diameter) in feet d/12 (recall the girth is given in

inches, not feet; 12 inches in one foot) are:

Cone: y =

π(d/12)

;

Cylinder: y =

π(d/12)

Taking logarithms and simplifying,

Cone: μ = log(π/1728) + 2 log d + log h

Cylinder: μ = log(π/576) + 2 log d + log h

126 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3 .3 The volume, height and girth (diameter) for 31 felled black cherry trees in

the Allegheny National Forest, Pennsylvania (Example 3.3)

Girth Height Volume Girth Height Volume

(in inches) (in feet) (in cubic feet) (in inches) (in feet) (in cubic feet)

8.3 70 10.3 12.9 85 33.8

8.6 65 10.3 13.3 86 27.4

8.8 63 10.2 13.7 71 25.7

10.5 72 16.4 13.8 64 24.9

10.7 81 18.8 14.0 78 34.5

10.8 83 19.7 14.2 80 31.7

11.0 66 15.6 14.5 74 36.3

11.0 75 18.2 16.0 72 38.3

11.1 80 22.6 16.3 77 42.6

11.2 75 19.9 17.3 81 55.4

11.3 79 24.2 17.5 82 55.7

11.4 76 21.0 17.9 80 58.3

11.4 76 21.4 18.0 80 51.5

11.7 69 21.3 18.0 80 51.0

12.0 75 19.1 20.6 87 77.0

12.9 74 22.2

where μ = E[log y]. Plotting the logarithm of volume against the logarithm

of girth and height (Fig. 3.16, bottom panels) shows approximately linear

relationships:

> plot( log(Volume)~log(Height), data=trees, pch=19, xlab="log(Height)",

ylab="log(Volume)", main="Log(Volume) vs log(Height)", las=1)

> plot( log(Volume)~log(Girth), data=trees, pch=19, xlab="log(Girth)",

ylab="log(Volume)", main="Log(Volume) vs log(Girth)", las=1)

Since the cone and cylinder are only approximations, enforcing the param-

eters to the above values may be presumptuous. Instead, consider the more

general model with the form

log μ = β

+ β

log d + β

log h.

If the assumptions about the tree shapes are appropriate, expect β

≈ 2

and β

≈ 1. The value of β

may give an indication of whether the cone

(β

≈ log(π/1728) = −6.310) or the cylinder (β

≈ log(π/576) = −5.211) is

a better approximation to the shape.

To ﬁt the suggested model in r:

> m.trees <- lm( log(Volume)~log(Girth)+log(Height), data=trees)

> printCoefmat( coef(summary(m.trees)))

Estimate Std. Error t value Pr(>|t|)

(Intercept) -6.631617 0.799790 -8.2917 5.057e-09 ***

log(Girth) 1.982650 0.075011 26.4316 < 2.2e-16 ***

log(Height) 1.117123 0.204437 5.4644 7.805e-06 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

3.11 Polynomial Trends 127

65 70 75 80 85

Volume vs height

Height (feet)

Volume (cubic feet)

8101214161820

Volume vs girth

Girth (inches)

Volume (cubic feet)

4.15 4.25 4.35 4.45

2.5

3.0

3.5

4.0

Log(Volume) vs log(Height)

log(Height)

log(Volume)

l l

2.2 2.4 2.6 2.8 3.0

2.5

3.0

3.5

4.0

Log(Volume) vs log(Girth)

log(Girth)

log(Volume)

Fig. 3.16 The volume of timber from 31 cherry trees plotted against the tree height

(top left panel) and against tree girth (top right panel). The bottom panels show the

logarithm of volume against logarithm of height (bottom left panel) and logarithm of

volume against logarithm of girth (bottom right panel) (Example 3.14)

Observe that

= −6.632 is close to the value expected if trees were approx-

imated as cones. In addition,

≈ 2and

≈ 1 as expected. 

3.11 Polynomial Trends

The covariate transformations discussed in the previous section are simple

and commonly used. Sometimes, however, the relationship between the re-

sponse and the covariates is more complicated than can be described by sim-

ple transformations of the covariates. A more general possibility is to build

a polynomial trend as a function of one of the covariates. The higher the

128 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3.4 The heat capacity C

of hydrogen bromide (in calories/(mole.K)) and the

temperature (in K) (Example 3.15)

Temperature C

Temperature

10.79 118.99 10.98 132.41 11.40 158.03

10.80 120.76 11.03 135.89 11.61 162.72

10.86 122.71 11.08 139.02 11.69 167.67

10.93 125.48 11.10 140.25 11.91 172.86

10.99 127.31 11.19 145.61 12.07 177.52

10.96 130.06 11.25 153.45 12.32 182.09

120 130 140 150 160 170 180

11.0

11.5

12.0

Heat capacity versus temperature

Temp (in Kelvin)

Heat capacity (cal/(mol.K))

Fig. 3.17 The heat capacity of hydrogen bromide plotted against temperature

(Example. 3.15)

degree of the polynomial, the greater the complexity of the trend that can be

ﬁtted. Unlike covariate transformations, which do not increase the number

of covariates in the model, polynomial trends involve adding new terms to

linear predictor, such as x

and x

, which are powers of the original covariate.

Example 3.15. Consider the heat capacity (C

) of solid hydrogen bromide

(HBr) [17, 31] as a function of temperature (Table 3.4; data set: heatcap).

The relationship between heat capacity and temperature is clearly non-linear

(Fig. 3.17):

> data(heatcap)

> plot( Cp ~ Temp, data=heatcap, main="Heat capacity versus temperature",

xlab="Temp (in Kelvin)", ylab="Heat capacity (cal/(mol.K))", las=1)

First note that the variation in the responses appears approximately con-

stant, and that the relationship is nonlinear. However, simple transformations

like log x are unlikely to work well for these data as the relationship is more

3.11 Polynomial Trends 129

complex; polynomials may be suitable. Care is needed when adding powers

of covariates to the systematic component in r. For example, this command

does not produce the required result:

> lm( Cp ~ Temp + Temp^2, data=heatcap) ### INCORRECT!

The above command fails, because the ^ symbol is interpreted in a formula

as crossing terms in the formula, and not as the usual arithmetic instruction

to raise Temp to a power. To tell r to interpret ^ arithmetically, we insulate

the terms (or inhibit interpretation as a formula operator) by using I():

> hc.col <- lm( Cp ~ Temp + I(Temp^2), data=heatcap)

Observe that the correlations between the two predictors are extremely close

to plus or minus one.

> summary(hc.col, correlation=TRUE)$correlation

(Intercept) Temp I(Temp^2)

(Intercept) 1.0000000 -0.9984975 0.9941781

Temp -0.9984975 1.0000000 -0.9985344

I(Temp^2) 0.9941781 -0.9985344 1.0000000

This is not uncommon when x, x

, x

and similar higher powers (referred to

as the raw polynomials) are used as model explanatory variables. Correlated

covariates may cause diﬃculties and confusion in model selection, and are

discussed more generally in Sect. 3.14. More numerically stable polynomials

are usually ﬁtted, called orthogonal polynomials, using poly() in r. For the

heat capacity data, we can ﬁt four polynomial models using poly(),and

compare:

> hc.m1 <- lm( Cp ~ poly(Temp, 1), data=heatcap) # Linear

> hc.m2 <- lm( Cp ~ poly(Temp, 2), data=heatcap) # Quadratic

> hc.m3 <- lm( Cp ~ poly(Temp, 3), data=heatcap) # Cubic

> hc.m4 <- lm( Cp ~ poly(Temp, 4), data=heatcap) # Quartic

The correlations between the estimated regression parameters are now zero

to computer precision. For example:

> summary(hc.m2, correlation=TRUE)$correlation

(Intercept) poly(Temp, 2)1 poly(Temp, 2)2

(Intercept) 1.000000e+00 3.697785e-32 -3.330669e-16

poly(Temp, 2)1 3.697785e-32 1.000000e+00 -1.110223e-16

poly(Temp, 2)2 -3.330669e-16 -1.110223e-16 1.000000e+00

> zapsmall( summary(hc.m2,correlation=TRUE)$correlation )

(Intercept) poly(Temp, 2)1 poly(Temp, 2)2

(Intercept) 1 0 0

poly(Temp, 2)1 0 1 0

poly(Temp, 2)2 0 0 1

Because the polynomials are orthogonal, the coeﬃcients of each ﬁtted poly-

nomial do not change when higher order polynomials are added to the model,

unlike the coeﬃcients when using the raw polynomials 1, x and x

130 3 Linear Regression Models: Diagnostics and Model-Building

120 140 160 180

10.5

11.0

11.5

12.0

12.5

Heat capacity vs temp:

Linear model

Temp (in K)

Heat capacity (cal/(mol.K))

120 140 160 180

10.5

11.0

11.5

12.0

12.5

Heat capacity vs temp:

Quadratic model

Temp (in K)

Heat capacity (cal/(mol K))

120 140 160 180

10.5

11.0

11.5

12.0

12.5

Heat capacity vs temp:

Cubic model

Temp (in K)

Heat capacity (cal/(mol K))

120 140 160 180

10.5

11.0

11.5

12.0

12.5

Heat capacity vs temp:

Quartic model

Temp (in K)

Heat capacity (cal/(mol K))

Fig. 3.18 Four models ﬁtted to the heat capacity data (Example 3.15)

> coef( hc.m1 )

(Intercept) poly(Temp, 1)

11.275556 1.840909

> coef( hc.m2 )

(Intercept) poly(Temp, 2)1 poly(Temp, 2)2

11.275556 1.840909 0.396890

> coef( hc.m3 )

(Intercept) poly(Temp, 3)1 poly(Temp, 3)2 poly(Temp, 3)3

11.2755556 1.8409086 0.3968900 0.1405174

Signiﬁcance tests show that the fourth order coeﬃcient is not required, so

the third-order polynomial is suﬃcient (Fig. 3.18):

> printCoefmat(coef(summary(hc.m4)))

Estimate Std. Error t value Pr(>|t|)

(Intercept) 11.2755556 0.0077737 1450.4766 < 2.2e-16 ***

poly(Temp, 4)1 1.8409086 0.0329810 55.8173 < 2.2e-16 ***

poly(Temp, 4)2 0.3968900 0.0329810 12.0339 2.02e-08 ***

poly(Temp, 4)3 0.1405174 0.0329810 4.2606 0.0009288 ***

poly(Temp, 4)4 -0.0556088 0.0329810 -1.6861 0.1156150

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

3.12 Regression Splines 131

11.0 11.5 12.0

−2

−1

Fitted values

Standardized residuals

120 130 140 150 160 170 180

−2

−1

Temp (in K)

Standardized residuals

−2 −1 0 1 2

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

51015

0.0

0.1

0.2

0.3

0.4

Index

cooks.distance(hc.m3)

Fig. 3.19 The diagnostic plots for the third-order polynomial model ﬁtted to the heat

capacity data (Example 3.15)

The diagnostics suggest no major problems with the cubic model, though

normality is perhaps suspect (Fig. 3.19):

> plot( rstandard(hc.m3) ~ fitted(hc.m3), las=1,

ylab="Standardized residuals", xlab="Fitted values" )

> plot( rstandard(hc.m3) ~ heatcap$Temp, las=1,

ylab="Standardized residuals", xlab="Temp (in K)" )

> qqnorm( rstandard( hc.m3 ), las=1 ); qqline( rstandard( hc.m3 ) )

> plot( cooks.distance(hc.m3), type="h", las=1)



3.12 Regression Splines

A more ﬂexible alternative to polynomial trends is to ﬁt a general-purpose

smooth curve which can take almost any shape. The simplest way to do this

is to use regression splines. Splines provide an objective and ﬂexible means

to ﬁt general but unknown curves.

A spline represents the relationship between y and x as a series of poly-

nomials, usually cubic polynomials, joined together at locations called knots,

in such a way to ensure a continuous relationship and continuous ﬁrst and

second derivatives (to ensure the polynomials join smoothly). The number of

132 3 Linear Regression Models: Diagnostics and Model-Building

polynomials to join together, and the degree of those polynomials (quadratic,

cubic, and so on) can be chosen by the user, depending on the type of spline

used. For each spline, the ﬁt is local to a subset of the observations; fewer

polynomials means a smoother curve and a simpler model.

The simplest approach to specify a spline curve is to specify a convenient

number of knots, depending on the complexity of the curve required, then ﬁt

the spline curve to the data by least squares. This approach is called regres-

sion splines. It is a type of linear regression with specially chosen covariates

that serve as a basis for the ﬁtted cubic polynomial curve. The number of

regression coeﬃcients used to a ﬁt a regression spline is known as the degrees

of freedom of the curve. The higher the degrees of freedom, the more complex

the trend that the curve can follow.

In r, splines may be ﬁtted using either bs() or ns(), both in the r package

splines which comes with r distributions. The function ns() ﬁts natural cubic

splines, which are splines with the second derivatives forced to zero at the

endpoints of the given interval, which are by default at the minimum and

maximum values of x. For a natural cubic spline, the degrees of freedom are

one more than the number of knots. bs() generates a B-spline basis for a cubic

spline. For a cubic B-spline, the degrees of freedom is one plus the number

of knots including the boundary knots at the minimum and maximum values

of x; in other words the number of internal knots plus three.

For either bs() or ns(), the complexity of the ﬁtted curve can be speciﬁed

by specifying the degrees of freedom or by explicitly specifying the locations

of the (internal) knots. The number of degrees of freedom is given using

df.Forbs(), the number of internal knots is df −degree under the default

settings, where degree is the degree of the polynomial (three by default). For

ns(), the number of internal knots is df −1 under the default settings. (This

is diﬀerent to bs() since the two functions treat the boundary conditions

diﬀerently.)

The location of the knots is given using the input knots. A common way

to do this is to use, for example,

bs(Temp, knots=quantile(Temp, c(.3, 0.6)), degree=2),

where the construct quantile(Temp, c(0.3, 0.6 ) locates the knots at the

30% and 60% quantiles of the data. (The Q% quantile is that value larger than

Q% of the observations.) By default, the knots are chosen at the quantiles of

x corresponding to equally spaced proportions.

Natural smoothing splines are linear at the end points, and hence can be

extrapolated in a predictable way outside the interval of the data used to

estimate the curve, unlike polynomials or B-splines which have relatively un-

predictable behaviour outside the interval. For this reason, natural smoothing

splines are a good practical choice in most cases for ﬁtting data-driven curves.

Example 3.16. Consider ﬁtting splines to the heat capacity data set

(Example 3.15; data set: heatcap). Fit a B-spline of degree=3 (that is,

cubic) and a natural cubic spline. Compare to the cubic polynomial ﬁtted

using

poly() chosen in Sect. 3.15 (p. 128), and use the same number of

degrees of freedom for all models:

3.12 Regression Splines 133

100 140 180

10.0

10.5

11.0

11.5

12.0

12.5

13.0

Using poly()

Temperature (in Kelvin)

Heat capacity

100 140 180

10.0

10.5

11.0

11.5

12.0

12.5

13.0

Using ns()

Temperature (in Kelvin)

Heat capacity

100 140 180

10.0

10.5

11.0

11.5

12.0

12.5

13.0

Using bs()

Temperature (in Kelvin)

Heat capacity

Fig. 3.20 The three cubic models ﬁtted to the heat capacity data (Example 3.16)

> library(splines)

> lm.poly <- lm( Cp ~ poly(Temp, 3), data=heatcap )

> lm.ns <- lm( Cp ~ ns(Temp, df=3), data=heatcap )

> lm.bs <- lm( Cp ~ bs(Temp, df=3), data=heatcap )

The models are not nested, so we use the aic to compare the models:

> extractAIC(lm.poly); extractAIC(lm.ns); extractAIC(lm.bs)

[1] 4.0000 -117.1234

[1] 4.0000 -119.2705

[1] 4.0000 -117.1234

The ﬁrst output from extractAIC() indicates that all models use the same

eﬀective number of parameters and so have the same level of complexity.

Of these three models, lm.ns has the smallest (closest to −∞) aic.The

ﬁtted models (Fig. 3.20) are reasonably similar over the range of the data

as expected. However, the behaviour of ns() near the endpoints is diﬀerent.

Recall ns() ﬁts natural cubic splines, forcing the second derivatives to zero

at the endpoints (Fig. 3.20, centre panel). 

Example 3.17. As more cubic polynomials are joined together in the spline

curve (and hence each is ﬁtted to fewer observations), the ﬁtted models be-

come more complex. Figure 3.21 is constructed using natural cubic splines

and the function ns(), but the ﬁtted splines are almost identical to those

produced with bs() and the same degrees of freedom. The dashed vertical

lines show the location of the knots partitioning the data; a cubic polynomial

is ﬁtted in each partition. By default the knots are located so that approx-

imately equal numbers of observations are between the knots, so where the

data are more concentrated around smaller values of Temp the knots are closer

together. 

134 3 Linear Regression Models: Diagnostics and Model-Building

120 140 160 180

11.0

11.5

12.0

ns(): 1 knot

Temperature (in Kelvin)

Heat capacity

120 140 160 180

11.0

11.5

12.0

ns(): 4 knots

Temperature (in Kelvin)

Heat capacity

120 140 160 180

11.0

11.5

12.0

ns(): 7 knots

Temperature (in Kelvin)

Heat capacity

Fig. 3.21 The heat capacity data, plotting C

against temperature using natural cubic

splines ns(). The dashed vertical lines are the locations of the knots on the horizontal

axis (Example 3.17)

3.13 Fixing Identiﬁed Outliers

After applying remedies to ensure linearity and constant variance, obser-

vations previously identiﬁed as outliers or as inﬂuential may no longer be

identiﬁed as such. Sometimes outliers or inﬂuential observations do remain,

however, or new ones may become apparent.

The ﬁrst step in dealing with outliers is to try to identify their cause. This

will lead to one of following conclusions:

• The observation is a known mistake. For example, too much herbicide

was accidentally used, the operator made a mistake using the machine,

or the observation was simply mis-recorded.

• The observation is known to come from a diﬀerent population. For ex-

ample, in an analysis of hospital admission rates, the outlier turns out on

closer examination to correspond to a hospital much larger than others

in the study.

• There is no known reason for why the observation might be an outlier.

When the outlier arises from an identiﬁable mistake, the ideal solution is

obviously to correct the mistake. For example, if a number was mis-recorded

and the correct value can still be recovered, then the data can be repaired.

If the mistake cannot be corrected, for example because it would require

re-running the experiment, then the oﬀending observation can be discarded.

This assumes that the occurrence of the mistake did not depend on the

value of the observation. If, for example, mistakes are more common for larger

values of the response than for smaller values, after a machine has been run

for some time perhaps, then more complex considerations come into play.

Little and Rubin [22] consider to what extent missing data or errors can

be accommodated into a statistical analysis when the errors depend on the

response variable of interest.

3.14 Collinearity 135

If the outlier arises from a diﬀerent population (such as ‘large hospitals’)

than the rest of the observations (‘small- and medium-sized hospitals’), then

again the outlier may safely be discarded. Any reporting of the results must

make it clear that the results do not apply to large hospitals, since that pop-

ulation of hospitals is not represented in the analysis. If there are a number

of observations from the secondary population (‘large hospitals’), not just

one or two, then the model might be augmented to allow separate parameter

values for the two populations, so that these observations could be retained.

When the cause of an outlier cannot be identiﬁed, the analyst is faced

with a dilemma. Simply discarding the observation is often unwise, since

that observation may be a real, genuine observation for which an alternative

model would be appropriate. An outlier that is not a mistake suggests that a

diﬀerent or more complex model may be necessary. One strategy to evaluate

the inﬂuence of the outlier is to ﬁt the model to the data with and without the

outlier. If the two models produce similar interpretations and conclusions for

the researcher, then the outlier is unimportant, whether discarded or not. If

the two models are materially diﬀerent, perhaps other types of models should

be considered. At the very least, note the observation and discuss the eﬀect

of the observation on the model.

3.14 Collinearity

Collinearity, sometimes called multicollinearity, occurs when some of the co-

variates are highly correlated with each other, implying that they measure

almost the same information.

Collinearity means that diﬀerent combinations of the covariates may lead

to nearly the same ﬁtted values. Collinearity is therefore mainly a problem

for interpretation rather than prediction (Sect. 1.9). Very strong collinearity

can theoretically cause numerical problems during the model ﬁtting, but this

is seldom a problem in practice with modern numerical software. Collinearity

does cause the estimated regression coeﬃcients to be highly dependent on

other variables in the linear predictor, making direct interpretation virtually

impossible.

A symptom of collinearity is that the standard errors of the aﬀected re-

gression coeﬃcients become large. If two covariates are very highly correlated,

typically only one of them needs to be retained in the model, but either one

would do equally well from a statistical point of view. In these cases, there

will exist many diﬀerent linear predictors all of which compute virtually the

same predictions, but with quite diﬀerent coeﬃcients for individual variables.

Collinearity means that separating causal variables from associated (passen-

ger) variables is especially diﬃcult, perhaps impossible.

136 3 Linear Regression Models: Diagnostics and Model-Building

Collinearity is most easily identiﬁed by examining the correlations between

the covariates. Correlations close to one in absolute value are of concern.

Other methods also exist for identifying collinearity.

A special case of collinearity occurs when a covariate and a power of the

covariate are included in the same model, such as x and x

(Example 3.15): x

and x

are almost inevitably highly correlated. Using orthogonal polynomials

or regression splines (Sect. 3.12) avoids this problem.

If collinearity is detected or suspected, remedies include:

• Omitting some explanatory variables from the analysis, since collinearity

implies the explanatory variables contain almost the same information.

Favour omitting explanatory variables with less theoretical basis for be-

longing in the model, whose interpretation is less clear, or are harder to

collect or measure. However, in practice, researchers tend to be reluctant

to throw away data.

• Combine explanatory variables in the model provided the combination

makes sense. For example, if height and weight are highly correlated,

consider combining the explanatory variables as the body mass index, or

bmi, and use this explanatory variable in the model in place of height

and weight. (bmi is weight (in kg), divided by the square of height (in

m).)

• Collect more data, if there are observations that can be made that better

distinguish the correlated covariates. Sometimes the covariates are intrin-

sically correlated, so collinearity is diﬃcult to remove regardless of data

collection.

• Use special methods, such as ridge regression [39, §11.2], which are beyond

the scope of this book.

Example 3.18. The monthly maintenance hours associated with maintaining

the anaesthesiology service for twelve naval hospitals in the usa was col-

lected (Table 3.5; data set: nhospital) together with some possible explana-

tory variables [26]. All explanatory variables appear strongly related to the

response (Fig. 3.22):

Tabl e 3. 5 Naval hospital maintenance data. MainHours is the monthly maintenance

hours; Eligible is the eligible population per thousand; OpRooms is the number of op-

erating rooms; Cases is the number of surgical cases (Example 3.18)

MainHours Eligible OpRooms Cases MainHours Eligible OpRooms Cases

304.37 25.5 4 89 383.78 43.4482

2616.32 294.3 11 513 2174.27 165.2 10 427

1139.12 83.7 4 231 845.30 74.3 4 193

285.43 30.7 2 68 1125.28 60.8 5 224

1413.77 129.8 6 319 3462.60 319.2 12 729

1555.68 180.8 6 276 3682.33 376.2 12 951

3.14 Collinearity 137

0 400 800

1000

2000

3000

4000

Cases

Maintenance hours

0 100 300

1000

2000

3000

4000

Eligible pop./thousand

Maintenance hours

02468 12

1000

2000

3000

4000

Operating rooms

Maintenance hours

Fig. 3.22 Plots of the naval hospital data (Example 3.18)

> data(nhospital); names(nhospital)

[1] "Cases" "Eligible" "OpRooms" "MainHours"

> plot( MainHours~Cases, data=nhospital, las=1, pch=19,

ylim=c(0, 4000), xlim=c(0, 1000),

xlab="Cases", ylab="Maintenance hours")

> plot( MainHours~Eligible, data=nhospital, las=1, pch=19,

ylim=c(0, 4000), xlim=c(0, 400),

xlab="Eligible pop./thousand", ylab="Maintenance hours")

> plot( MainHours~OpRooms, data=nhospital, las=1, pch=19,

ylim=c(0, 4000), xlim=c(0, 12),

xlab="Operating rooms", ylab="Maintenance hours")

The variables are all highly correlated:

> cor( nhospital)

Cases Eligible OpRooms MainHours

Cases 1.0000000 0.9602926 0.9264237 0.9802365

Eligible 0.9602926 1.0000000 0.9399181 0.9749010

OpRooms 0.9264237 0.9399181 1.0000000 0.9630730

MainHours 0.9802365 0.9749010 0.9630730 1.0000000

The correlations are all very close to one, implying many models exists which

give very similar predictions (Problem 3.7).

Consider ﬁtting the model:

> nh.m1 <- lm( MainHours ~ Eligible + OpRooms + Cases, data=nhospital)

Since the correlations are very high between the response and explanatory

variables, strong relationships between MainHours and each covariate are

expected after ﬁtting the model. However, the results of the t-tests for this

model show no evidence of strong relationships:

> printCoefmat( coef( summary( nh.m1 ) ) )

Estimate Std. Error t value Pr(>|t|)

(Intercept) -114.58953 130.33919 -0.8792 0.40494

Eligible 2.27138 1.68197 1.3504 0.21384

138 3 Linear Regression Models: Diagnostics and Model-Building

OpRooms 99.72542 42.21579 2.3623 0.04580 *

Cases 2.03154 0.67779 2.9973 0.01714 *

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The t-tests suggest OpRooms and Cases are mildly signiﬁcant in the model

after adjusting for Eligible, but Eligible is not signiﬁcant after adjust-

ing for the other explanatory variables. In contrast, consider the sequential

anova F -tests:

> anova( nh.m1 )

Analysis of Variance Table

Response: MainHours

Df Sum Sq Mean Sq F value Pr(>F)

Eligible 1 14346071 14346071 523.7574 1.409e-08 ***

OpRooms 1 282990 282990 10.3316 0.01234 *

Cases 1 246076 246076 8.9839 0.01714 *

Residuals 8 219125 27391

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

In the anova table, Eligible is highly signiﬁcant, and shows a very small

P -value. Since these F -tests are sequential, this test has not adjusted for any

other explanatory variable, so the result is strong as expected. After Eligible

is in the model, the other explanatory variable have little contribution to

make because the explanatory variables are highly correlated. 

3.15 Case Studies

3.15.1 Case Study 1

Consider the dmft data (data set: dental) ﬁrst seen in Sect. 2.13 (p. 76). In

that section, the model ﬁtted to the data was:

> data(dental)

> dental.lm <- lm( DMFT ~ Sugar * Indus, data=dental)

Consider some diagnostic plots (Fig. 3.23, top panels):

> scatter.smooth( rstandard(dental.lm) ~ fitted(dental.lm),

xlab="Fitted values", ylab="Standardized residuals", las=1)

> qqnorm( rstandard( dental.lm ), las=1 ); qqline( rstandard( dental.lm ) )

> plot( cooks.distance(dental.lm), type="h", las=1)

The plots are acceptable, though the Q–Q plot is not ideal. However, one ob-

servation has a large residual of r



=3.88 (top left panel; top centre panel).

3.15 Case Studies 139

1.5 2.5 3.5

−1

Fitted values

Standardized residuals

−2 0 1 2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

0 20406080

0.00

0.02

0.04

0.06

0.08

0.10

0.12

0.14

Index

cooks.distance(dental.lm)

0.2 0.6 1.0 1.4

−3

−2

−1

Fitted values

Standardized residuals

−2 0 1 2

−3

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

0 20406080

0.00

0.01

0.02

0.03

0.04

0.05

0.06

Index

Cook's distance, D

Fig. 3.23 Diagnostic plots of the model ﬁtted to the dmft data. Top panels: using

dmft as the response; bottom panels: using the logarithm of dmft as the response

(Sect. 3.15.1)

The inﬂuence diagnostics reveal that two observations are inﬂuential accord-

ing to dffits, but none are inﬂuential according to Cook’s distance or df-

betas:

> im <- influence.measures(dental.lm)

> colSums(im$is.inf)

dfb.1_ dfb.Sugr dfb.InNI dfb.S:IN dffit cov.r cook.d hat

000021102

DMFT is a strictly positive response variable that varies over an order of

magnitude between countries, so a log-transformation may well be helpful:

> dental.lm.log <- update(dental.lm, log(DMFT) ~ .)

> anova(dental.lm.log)

Analysis of Variance Table

Response: log(DMFT)

Df Sum Sq Mean Sq F value Pr(>F)

Sugar 1 10.9773 10.9773 36.8605 3.332e-08 ***

Indus 1 0.6183 0.6183 2.0761 0.15326

Sugar:Indus 1 1.3772 1.3772 4.6245 0.03432 *

140 3 Linear Regression Models: Diagnostics and Model-Building

Residuals 86 25.6113 0.2978

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Now examine the diagnostics of this new model (Fig. 3.23, bottom panels):

> scatter.smooth( rstandard(dental.lm.log) ~ fitted(dental.lm.log),

xlab="Fitted values", ylab="Standardized residuals", las=1)

> qqnorm( rs <- rstandard( dental.lm.log ), las=1 ); qqline( rs )

> plot( cooks.distance(dental.lm.log), type="h", las=1,

ylab="Cook's distance, D")

Each diagnostic plot is improved: the variance of the standardized residuals

appears approximately constant and the slight curvature is gone; the residuals

appear more normally distributed; and the largest absolute residual is much

smaller. Furthermore, the two observations identiﬁed as inﬂuential according

to dffits are no longer declared inﬂuential:

> im <- influence.measures(dental.lm.log); colSums(im$is.inf)

dfb.1_ dfb.Sugr dfb.InNI dfb.S:IN dffit cov.r cook.d hat

000001102

The ﬁnal model is:

> printCoefmat(coef( summary(dental.lm.log)) )

Estimate Std. Error t value Pr(>|t|)

(Intercept) 1.3871066 0.5102055 2.7187 0.007926 **

Sugar -0.0058798 0.0119543 -0.4919 0.624075

IndusNonInd -1.2916000 0.5253985 -2.4583 0.015964 *

Sugar:IndusNonInd 0.0272742 0.0126829 2.1505 0.034325 *

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Sugar is retained due to the marginality principle. The two ﬁtted models are

shown in Fig. 3.24. The model can be written as



∼ N(μ

=0.298)

=1.387 − 0.005880x

− 1.292x

+0.02727x

where E[log y

]=μ

, x

is the mean annual sugar consumption (in kg/per-

son/year) and x

= 1 for industrialized countries (and is 0 otherwise). More

directly, the systematic component is

E[log y

]=μ



1.387 − 0.005880x

for industrialized countries

0.09551 + 0.02139x

for non-industrialized countries.

The two models (using the response as DMFT or log(DMFT)) can be com-

pared using the aic and bic:

> # AIC

> c( "AIC (DMFT)" = extractAIC(dental.lm)[2],

"AIC (log-DMFT)" = extractAIC(dental.lm.log)[2] )

3.15 Case Studies 141

0 102030405060

No transformation

Mean annual sugar consumption

Mean DMFT at age 12

Industrialized

Non−industrialized

0 102030405060

Log transformation

Mean annual sugar consumption

Mean DMFT at age 12

Industrialized

Non−industrialized

Fig. 3.24 Two models ﬁtted to the dmft data. Left panel: using dmft as the response;

right panel: using the logarithm of dmft as the response (Sect. 3.15.1)

AIC (DMFT) AIC (log-DMFT)

61.36621 -105.10967

> # BIC

> k <- nobs(dental.lm) # The penalty to compute the BIC

> c( "BIC (DMFT)" = extractAIC(dental.lm, k=k )[2],

"BIC (log-DMFT)" = extractAIC(dental.lm.log, k=k )[2])

BIC (DMFT) BIC (log-DMFT)

413.3662 246.8903

In both cases, the model using log(DMFT) as the response variable is pre-

ferred.

For industrialized countries, the mean number of dmft at age 12 in-

creases approximately by a factor of exp(−0.005880) = 0.9941 for each

1 kg/person/year increase in sugar consumption, which is not statistically

signiﬁcant. For non-industrialized countries, the mean number of dmft at

age 12 increases by approximately a factor of exp(0.02139) = 1.022 for each

1 kg/person/year increase in sugar consumption.

The limitations in the study (identiﬁed in Sec. 2.13) remain, though the

ﬁtted model is now slightly better according to the diagnostics.

3.15.2 Case Study 2

To understand the how the chemical composition of cheese is related to its

taste, a study [25, 34] from the La Trobe Valley in Victoria (Australia) had

142 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3. 6 The chemical composition and tastes of samples of cheddar cheese

(Sect. 3.15.2)

Taste Acetic H2S Lactic Taste Acetic H2S Lactic

12.3 94 23 0.86 40.9 581 14,589 1.74

20.9 174 155 1.53 15.9 120 50 1.16

39.0 214 230 1.57 6.4 224 110 1.49

47.9 317 1801 1.81 18.0 190 480 1.63

5.6 106 45 0.99 38.9 230 8639 1.99

25.9 298 2000 1.09 14.0 96 141 1.15

37.3 362 6161 1.29 15.2 200 185 1.33

21.9 436 2881 1.78 32.0 234 10,322 1.44

18.1 134 47 1.29 56.7 349 26,876 2.01

21.0 189 65 1.58 16.8 214 39 1.31

34.9 311 465 1.68 11.6 421 25 1.46

57.2 630 2719 1.90 26.5 638 1056 1.72

0.7 88 20 1.06 0.7 206 50 1.25

25.9 188 140 1.30 13.4 331 800 1.08

54.9 469 856 1.52 5.5 481 120 1.25

samples of cheddar cheese chemically analysed. For each cheese, the acetic

acid concentration (Acetic), the lactic acid concentration (Lactic), and the

S concentration (H2S) were measured. The cheeses were also scored for

their taste (Table 3.6; data set: cheese), and the ﬁnal Taste score combines

the taste scores from several judges.

Plotting the response Taste against the explanatory variables shows pos-

sible relationships between the variables (Fig. 3.25):

> data(cheese); names(cheese)

[1] "Taste" "Acetic" "H2S" "Lactic"

> plot( Taste ~ Acetic, data=cheese, las=1, pch=19,

xlab="Acetic acid concentration", ylab="Taste score")

> plot( Taste ~ H2S, data=cheese, las=1, pch=19,

xlab="H2S concentration", ylab="Taste score")

> plot( Taste ~ Lactic, data=cheese, las=1, pch=19,

xlab="Lactic acid concentration", ylab="Taste score")

First consider the variance of y. The plot of Taste against Lactic shows

little evidence of non-constant variance (Fig. 3.25, bottom left panel); the

plot of Taste against Acetic suggests the variance slightly increases as the

mean taste score increases (top left panel). The plot of Taste against H2S is

diﬃcult to interpret (top right panel) as most values of H2S are small, but

some are very large.

The relationships between Taste and Acetic, and also between Taste

and Lactic, appear approximately linear. The relationship between Taste

against H2S is non-linear, and the observations with large values of H2S will

3.15 Case Studies 143

100 200 300 400 500 600

Acetic acid concentration

Taste score

0 5000 15000 25000

H2S concentration

Taste score

1.0 1.2 1.4 1.6 1.8 2.0

Lactic acid concentration

Taste score

46810

log(H2S concentration)

Taste score

Fig. 3.25 The cheese data. The mean taste score plotted against the acetic acid concen-

tration (top left panel); the mean taste score plotted against the H

S concentration (top

right panel); the mean taste score plotted against the lactic acid concentration (bottom

left panel); the mean taste score plotted against the logarithm of H

S concentration

(bottom right panel) (Sect. 3.15.2)

certainly be inﬂuential. Since H2S covers many orders of magnitude (from 20

to 26, 880), consider taking logarithms (Fig. 3.25, bottom right panel):

> plot( Taste ~ log(H2S), data=cheese, las=1, pch=19,

xlab="log(H2S concentration)", ylab="Taste score")

The relationship between Taste and log(H2S) now appears approximately

linear. The variance of Taste appears to be slightly increasing as log(H2S)

increases. Some, but not all, evidence suggests the variation is slightly in-

creasing for increasing taste scores. For the moment, we retain Taste as the

response without transforming, and examine the diagnostics to determine if

a transformation is necessary.

Begin with the full model, including all interactions:

> cheese.m1 <- lm( Taste ~ Acetic * log(H2S) * Lactic, data=cheese )

> drop1(cheese.m1, test="F")

Single term deletions

144 3 Linear Regression Models: Diagnostics and Model-Building

Model:

Taste ~ Acetic * log(H2S) * Lactic

Df Sum of Sq RSS AIC F value Pr(>F)

<none> 2452.3 148.11

Acetic:log(H2S):Lactic 1 36.467 2488.8 146.55 0.3272 0.5731

The three-way interaction is not needed. Then consider dropping each two-

way interaction in turn:

> cheese.m2 <- update( cheese.m1, . ~ (Acetic + log(H2S): + Lactic)^2 )

> drop1(cheese.m2, test="F")

Single term deletions

Model:

Taste ~ Acetic + log(H2S):Lactic + Acetic:log(H2S):Lactic

Df Sum of Sq RSS AIC F value Pr(>F)

<none> 2679.1 142.76

Acetic:log(H2S):Lactic 1 24.269 2703.4 141.03 0.2355 0.6315

No two-way interactions are needed either. Finally, consider dropping each

main eﬀect term:

> cheese.m3 <- lm( Taste ~ log(H2S) + Lactic + Acetic, data=cheese )

> drop1(cheese.m3, test="F")

Single term deletions

Model:

Taste ~ log(H2S) + Lactic + Acetic

Df Sum of Sq RSS AIC F value Pr(>F)

<none> 2660.9 142.56

log(H2S) 1 1012.39 3673.3 150.23 9.8922 0.004126 **

Lactic 1 527.53 3188.4 145.98 5.1546 0.031706 *

Acetic 1 8.05 2668.9 140.65 0.0787 0.781291

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The most suitable model appears to be:

> cheese.m4 <- lm( Taste ~ log(H2S) + Lactic, data=cheese )

> coef( summary(cheese.m4) )

Estimate Std. Error t value Pr(>|t|)

(Intercept) -27.591089 8.981801 -3.071888 0.004813785

log(H2S) 3.946425 1.135722 3.474817 0.001742652

Lactic 19.885953 7.959175 2.498494 0.018858866

While all three covariates appear associated with Taste (Fig. 3.25,p.143),

only two are necessary in the model. This implies the covariates are corre-

lated:

> with(cheese, cor( cbind(Taste, Acetic, logH2S=log(H2S), Lactic) ) )

Taste Acetic logH2S Lactic

Taste 1.0000000 0.5131983 0.7557637 0.7042362

Acetic 0.5131983 1.0000000 0.5548159 0.5410837

logH2S 0.7557637 0.5548159 1.0000000 0.6448351

Lactic 0.7042362 0.5410837 0.6448351 1.0000000

3.15 Case Studies 145

010 30 50

−1

Std resids vs fitted values

Fitted values

Standardized residuals

−2 −1 0 1 2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

0 5 10 20 30

0.00

0.02

0.04

0.06

0.08

0.10

0.12

Cook's distance values

Index

Cook's distance, D

100 300 500

−1

Std residuals vs Acetic

Acetic acid concentration

Standardized residuals

46810

−1

Std residuals vs log(H2S)

log(H2S concentration

Standardized residuals

1.0 1.4 1.8

−1

Std residuals vs Lactic

Lactic acid concentration

Standardized residuals

Fig. 3.26 The diagnostics from the model ﬁtted to the cheese-tasting data (Sect. 3.15.2)

Clearly, the relationships between Taste and Lactic, and between Taste and

log(H2S), are stronger than that between Taste and Acetic. Furthermore,

Acetic is correlated with both Lactic and log(H2S), so once Lactic and

log(H2S) are in the model Acetic has almost nothing further to contribute:

> cor( cbind(rstandard(cheese.m3), cheese$Acetic))

[,1] [,2]

[1,] 1.000000000 -0.002230637

[2,] -0.002230637 1.000000000

Consider the diagnostics of the ﬁnal model (Fig. 3.26):

> scatter.smooth( rstandard(cheese.m4) ~ fitted(cheese.m4), las=1,

main="Std resids vs fitted values",

xlab="Fitted values", ylab="Standardized residuals")

> qqnorm( rstandard(cheese.m4), las=1); qqline( rstandard(cheese.m4) )

> plot( cooks.distance(cheese.m4), type="h", las=1,

main="Cook's distance values", ylab="Cook's distance, D")

> scatter.smooth( rstandard(cheese.m4) ~ cheese$Acetic,

main="Std residuals vs Acetic", las=1,

xlab="Acetic acid concentration", ylab="Standardized residuals")

> scatter.smooth( rstandard(cheese.m4) ~ log(cheese$H2S),

main="Std residuals vs log(H2S)", las=1,

xlab="log(H2S concentration", ylab="Standardized residuals")

146 3 Linear Regression Models: Diagnostics and Model-Building

> scatter.smooth( rstandard(cheese.m4) ~ cheese$Lactic,

main="Std residuals vs Lactic", las=1,

xlab="Lactic acid concentration", ylab="Standardized residuals")

The model diagnostics suggest the model cheese.m4 is adequate, although a

single observation with a standardized residual just larger than 2 makes the

variance appear larger in the centre of some plots. No observation appears

substantially more inﬂuential than the others based on the Cook’s distance,

dffits or dfbetas:

> im <- influence.measures(cheese.m4); colSums(im$is.inf)

dfb.1_ dfb.l(H2 dfb.Lctc dffit cov.r cook.d hat

0000400

The ﬁtted model cheese.m4 shows that the taste improves, on average,

with increasing concentrations of lactic acid and H

S. Because of the high cor-

relations between Lactic and H2S, interpreting the individual contributions

of each chemical to the taste is not straightforward.

3.16 Using R for Diagnostic Analysis of Linear

Regression Models

An introduction to using r is given in Appendix A. For ﬁtting linear regres-

sion models, the function lm() is used (see Sect. 2.14,p.79 for more on the

use of lm()). This section summarizes and collates r commands relevant to

diagnostic analysis of linear regression models.

Three types of residuals may be computed from a ﬁtted model, say fit,

using r:

• Raw residuals (Sect. 3.3): Use resid(fit) or residuals(fit).

• Standardized residuals r



(Sect. 3.3): Use rstandard(fit).

• Studentized residuals r



(Sect. 3.6.2): Use rstudent(fit).

Diﬀerent measures of inﬂuence may be computed in r (Sect. 3.6.3):

• Cook’s distance D:Usecooks.distance(fit).

• dfbetas:Usedfbetas(fit).

• dffits:Usedffits(fit).

• Covariance ratio cr:Usecovratio(fit).

All these measures of inﬂuence, together with the leverages h, are returned us-

ing influence.measures(fit). Observations of potential interest are ﬂagged

according to the criteria explained in Sect. 3.6.3 (p. 110). Other useful r com-

mands for diagnostics analysis include:

• Q–Q plots: Use qqnorm(), where the input is a function to produce resid-

uals from a ﬁtted model fit, such as rstandard(fit). Add a reference

line by following the qqnorm() call with qqline() with the same input.

• Fitted values ˆμ:Usefitted(fit).

• Leverages h:Usehatvalues(fit).

3.17 Summary 147

A ﬁtted model can be plotted also; for example:

> model <- lm( y ~ x); plot( model )

These commands produce four residual plots by default; see ?plot.lm.

r commands useful for remedying problems include:

•Thepoly() function (Sect. 3.12) is used to add orthogonal polynomi-

als to the systematic component. To use poly(), supply the name of

the covariate x, and the degree of the polynomial to ﬁt. Typical use:

poly(Ht, degree=4) which ﬁts a quartic in Ht.

• The spline functions ns() (to ﬁt natural cubic splines) and bs() (to

ﬁt splines of any degree) are in package splines which comes with r

(Sect. 3.12).

To use ns(), supply the name of the covariate, and either the degrees

of freedom using df or the location of the internal knots using knots.

Typical use: ns(Ht, df=3), which ﬁts a natural cubic spline with three

degrees of freedom.

To use bs(), supply the name of the covariate, the degree of the polyno-

mials to use, and either the degrees of freedom using df or the location of

the internal knots using knots. Typical use: bs(Ht, df=3, degree=2),

which ﬁts quadratic splines with three degrees of freedom.

• Transformations of the responses (Sect. 3.9) or the covariates (Sect. 3.10)

are computed using standard r functions, such as sqrt(x), log(y), 1/x,

asin(sqrt(y)),andy^(-2). When used with covariates in lm(),the

transformation should be insulated using I(); for example, I(1/x).

• The Box–Cox transformation may be chosen using the boxcox() func-

tion in package MASS (which comes with r), designed to identify the

transformation most suitable for achieving linearity, normality and con-

stant variance simultaneously. Typical use: boxcox(FEV ~ Age + Ht +

Gender + Smoke).

3.17 Summary

Chapter 3 discusses methods for identifying possible violations of assumptions

in multiple regression models, and remedying these issues. The assumptions

for linear regression models are, in order of importance (Sect. 3.2):

• Lack of outliers: The model is appropriate for all observations.

• Linearity: The linear predictor captures the true relationship between μ

and the explanatory variables, and all important explanatory variables

are included.

• Constant variance: The responses y

have constant variance, apart from

known weights w

• Independence: The responses y

are independent of each other.

148 3 Linear Regression Models: Diagnostics and Model-Building

In addition, normal linear regression models assume the responses y come

from a normal distribution.

Diagnostic analysis is used to identify any deviations from these assump-

tions that are likely to aﬀect conclusions (Sect. 3.2), and the main tool for

diagnostic analysis is residuals. The three main types of residuals (Sects. 3.3

and 3.6.2) are raw residuals r

, standardized residuals r



, and Studentized

residuals r



. The standardized and Studentized residuals have approximately

constant variance of one, and are preferred in residual plots for this reason

(Sect. 3.3; Sect. 3.6.2). The terminology used for residuals is confusingly in-

consistent (Sect. 3.7). In addition to residuals, the leverages h

identify un-

usual combinations of the explanatory variable (Sects. 3.4).

A strategy for assessing models is (Sect. 3.5):

• Check for independence of the responses when possible. This assumption

can be hard to check, as this may be depend on the method of data col-

lection. However, if the data are collected over time, dependence may be

identiﬁed by plotting residuals against the previous residual in time. Like-

wise, if the data are spatial, check for dependence by plotting residuals

against spatial variables (Sect. 3.5.5).

• Check for linearity between the responses and all covariates using plots

of the residuals against each explanatory variable (Sect. 3.5.1). Linearity

between the response and explanatory variables after adjusting for the

eﬀects of the other explanatory variables can also be assessed using partial

residual plots (Sect. 3.5.2).

• Check for constant variance in the response using plots of the residuals

against ˆμ (Sect. 3.5.3).

• Check for normality of the responses using a Q–Q plot (Sect. 3.5.4).

Outliers are observations inconsistent with the rest of the observations

(Sect. 3.6.2), when the corresponding residuals are unusually large, positive

or negative. Outliers should be identiﬁed and, if necessary, appropriately

managed (Sect. 3.13).

Inﬂuential observations are outliers that substantially change the ﬁtted

model when omitted from the data set (Sect. 3.6.2). Numerical means for

identifying inﬂuence include Cook’s distance D, dffits, dfbetas,orthe

covariance ratio cr (Sect. 3.6.3).

Some strategies for solving model weaknesses are (Sect. 3.8):

• If the responses are not independent, use other methods.

• If the variance of the response is not approximately constant, transform

y as necessary (Sect. 3.9).

• Then, if the relationship is not linear, transform the covariates us-

ing simple transformations (Sect. 3.10), polynomials in the covariates

(Sect. 3.11), or regression splines (Sect. 3.12).

Finally, collinearity occurs when at least some of the covariates are highly

correlated with each other (Sect. 3.14).

3.17 Summary 149

Problems

Selected solutions begin on p. 532. Problems preceded by an asterisk * refer

to the optional sections in the text, and may require matrix manipulations.

3.1. The standardized residual r



measures the reduction in the rss (divided

by s

) when Observation i is omitted from the data. Demonstrate this in r

using the lungcap data as follows.

• Fit the model LC.lm (Example 3.1,p.97). Compute the rss, s

and the

standardized residuals from this model.

• Omit observation 1 from lungcap, and reﬁt the model without Observa-

tion 1. Call this model LC.omit1.

• Compute the diﬀerence between the rss for the full model LC.lm and for

model LC.omit1. Show that this diﬀerence divided by s

is the standard-

ized residuals squared for Observation 1.

Repeat the above process for every observation i, and show that the n diﬀer-

ences divided by s

are the standardized residuals squared.

*3.2.Consider the hat matrix as deﬁned in (3.3)(p.101).

1. Show that H is idempotent; that is, H

=H.

2. Show that H is symmetric; that is, H

=H.

3. Show I

− H is idempotent and symmetric.

*3.3.Consider a simple linear regression model, with all prior weights set

to one and including a constant term in the linear predictor.

1. Show that

− ¯x)



j=1

− ¯x)

2. Use this expression to show that h

≥ (1/n)

3. Show that h

≤ 1. Hint: Since H is idempotent (Problem 3.2), ﬁrst show



j=1

= h



j=i

*3.4.Equation (3.6)(p.110) gives an expression for Cook’s distance, which

can also be written as

(

μ −

(i)

)

(

μ −

(i)

)



. (3.9)

Interpret Cook’s distance using this form.

3.5. To gain experience reading Q–Q plots, use r to produce Q–Q plots of

data known to be generated randomly from a standard normal distribution

using rnorm(). Generate ten Q–Q plots based on 100 random numbers, and

comment on using Q–Q plots when n = 100. Repeat the exercise for n = 50,

20 and 10, and comment further.

150 3 Linear Regression Models: Diagnostics and Model-Building

3.6. Show that the partial residual plot for a simple linear regression model

is simply a plot of y against x.

3.7. For the naval hospital data (data set: nhospital) (Example 3.18,p.136),

ﬁt the three models that contain two of the explanatory variables. Show that

the ﬁtted values are very similar for all three models.

3.8. The lung capacity data [21] in Example 1.1 (data set: lungcap)have

been used often in Chaps. 2 and 3.

1. Fit the model with fev as the response and smoking status as the only

explanatory variable. Interpret the meaning of the coeﬃcient for smoking.

2. Fit the model with fev as the response and all other variables as explana-

tory variables (but do not use any interactions). Interpret the coeﬃcient

for smoking status.

3. Fit the model with the logarithm of fev as the response and all other

variables as explanatory variables (but do not use any interactions). In-

terpret the coeﬃcient for smoking status.

4. Determine a suitable model for the data.

3.9. In Chap. 2, the lung capacity data (data set: lungcap) was analysed

using log(FEV) as the response variable, with Ht as one of the explanatory

variables. In Example 3.13, a model was proposed for analysing log(FEV)

using log(Ht) in place of Ht as one of the covariates. Compare these two

models using a diagnostic analysis, and comment.

3.10. In Sect. 3.15.2 (p. 141), a model is ﬁtted to the cheese tasting data

(data set: cheese). However, before ﬁtting this model, the plot of Taste

against log(H2S) suggested slightly non-constant variance. An alternative

model might suggest using log(Taste) as the response rather than Taste.

Show that using log(Taste) as the response results in a poor model.

3.11. A study [27] compiled information about the food consumption habits

of various ﬁsh species (data set: fishfood). The ﬁtted linear regression model

has the form

log ˆμ = β

+ β

log MaxWt + β

log Temp + β

log AR + β

Food,

where μ =E[FoodCon] is the predicted daily food consumption as a percent-

age of biomass, F = 0 for carnivores, and F = 1 for herbivores, and the other

variables are deﬁned in Table 3.7.

1. Fit the model used in original study.

2. Perform a diagnostic analysis of this model.

3. Interpret the model.

4. Determine if a better model can be found by considering interaction

terms.

3.17 Summary 151

Tabl e 3 . 7 The daily food consumption (as a percentage of biomass) FoodCon,maximum

weight (in g) MaxWt, mean habitat temperature (in

◦

C) Temp,aspectratioAR, and food

type Food (where C means carnivore and H means herbivore) for various ﬁsh Species.

The ﬁrst six observations are shown (Problem 3.11)

Species MaxWt Temp AR Food FoodCon

Brevoortia patronus 362 25 1.69 C 2.22

Brevoortia tyrannus 1216 18 2.31 H 8.61

Engraulis encrasicholus 28 15 1.42 C 2.50

Hygophum proximum 2 25 1.65 C 9.28

Hygophum reindhardtii 1 25 1.05 C 6.66

Lampanyctus alatus 2 25 1.62 C 3.32

Tabl e 3 .8 Energy and digestibilities (‘Digest.’) of diets for sheep (Problem 3.12)

Dry matter Energy Digestible Dry matter Energy Digestible energy

digest. (%) digest. (%) energy (cal/gram) digest. (%) digest. (%) (cal/gram)

30.5 27.8 1.243 68.5 66.8 3.016

63.0 61.5 2.750 71.6 70.7 3.149

62.8 60.4 2.701 71.5 69.8 3.131

50.0 49.5 2.213 75.4 73.5 3.396

60.3 58.7 2.681 71.7 69.8 3.131

64.1 63.0 2.887 73.2 72.1 3.226

63.7 62.8 2.895 56.6 55.2 2.407

63.4 62.8 2.895 49.7 48.1 2.098

65.4 64.2 2.952 54.7 53.4 2.331

68.1 66.5 3.059 58.7 57.0 2.488

72.1 70.4 3.239 64.3 62.3 2.761

68.8 68.7 3.154 67.7 65.5 2.904

52.8 50.7 2.229 68.3 66.2 2.933

60.3 58.1 2.550 66.4 64.8 2.869

52.8 50.7 2.226 68.1 66.3 2.963

66.1 64.2 2.823 72.2 70.8 3.164

62.5 61.3 2.768 76.3 74.2 3.314

65.8 64.0 2.768 70.4 69.0 3.081

3.12. In a study [24] of the feed of ruminants, the data in Table 3.8 were

collected (data set: ruminant). The purpose of the study was to model the

digestible energy content, and explore the relationships with percentage dry

matter digestibility and percentage energy digestibility.

1. Plot the digestible energy content against the other two variables, and

comment on the relationships.

2. Compute the correlations between the three variables, and comment.

3. Fit a suitable simple linear regression model.

4. Perform a diagnostic analysis. In particular, one observation is diﬀerent to

the others: does the observation have a large residual or a high leverage?

152 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3 .9 The pH and wound size of for 20 lower-leg wounds on 17 patients (Prob-

lem 3.14)

Start End

Size (in cm

) pH Size (in cm

)pH

4.3 7.26 4.0 7.15

2.4 7.63 1.5 7.15

7.3 7.63 2.9 7.50

4.3 7.18 1.4 7.15

3.5 7.75 0.1 6.69

10.3 7.94 6.0 7.56

0.6 7.60 0.6 5.52

0.7 7.90 1.1 7.70

18.3 7.60 13.1 7.76

16.1 7.70 18.1 7.42

2.5 7.98 1.0 7.15

20.0 7.35 16.5 6.55

2.4 7.89 2.3 7.28

3.7 8.00 3.5 7.40

2.4 7.10 1.0 7.48

61.0 8.30 72.0 7.95

17.7 7.66 9.6 7.32

2.1 8.20 3.0 7.24

0.9 8.25 2.0 7.71

22.0 7.63 23.5 7.52

3.13. An experiment was conducted [30] to determine how to maximize

meadowfoam ﬂower production. The data and a fuller description are given

in Problem 2.15 (data set: flowers). In that problem, a linear regression

model was ﬁtted to the data.

1. Perform a diagnostic analysis on the ﬁtted linear regression model.

2. Identify any inﬂuential observations or outliers.

3. Interpret the ﬁnal model.

3.14. A study [15] of the eﬀect of Manuka honey of the healing of wounds

collected data from 20 wounds from 17 individuals (Table 3.9; data set:

manuka).

1. Plot the percentage reduction in wound size over 2 weeks against the

initial pH.

2. Fit the corresponding regression equation, and draw the regression line

on the plot.

3. Write down the regression model. Interpret the model. (This led to one

of the main conclusions of the paper.)

Later, a retraction notice was issued for the article [16] which stated that:

3.17 Summary 153

The regression results presented. . . are strongly inﬂuenced by a high outlying

value. . . When the results for this patient are omitted, the association is no longer

statistically signiﬁcant. . . As this relationship is pivotal to the conclusions of the

paper, it is felt that the interests of patient care would be best served by a retrac-

tion.

4. Perform a diagnostic analysis of the model ﬁtted above. Identify the ob-

servation that is inﬂuential.

5. Reﬁt the regression model without this inﬂuential observation, and write

down the model. Interpret the model, and compare to your interpretation

of the previous model.

6. Plot this regression line on the plot generated above. Compare the two

regression lines, and comment.

3.15. A study of babies [4] hypothesized that babies would take longer to

learn to crawl in colder months because the extra clothing restricts their

movement (data set: crawl). The data and a fuller description are given in

Problem 2.16 (p. 87). In that problem, a linear regression model was ﬁtted

to the data.

1. Perform a diagnostic analysis of the ﬁtted linear regression model.

2. Identify any inﬂuential observations or outliers.

3. Suppose some of the babies were twins. Which assumption would be

violated by the inclusion of these babies in the study? Do you think this

would have practical implications?

3.16. Children were asked to build towers out of cubical and cylindrical

blocks as high as they could [20, 33], and the number of blocks used and the

time taken were recorded. The data (data set: blocks) and a fuller descrip-

tion are given in Problem 2.18 (p. 88). In that problem, a linear regression

model was ﬁtted to model the time to build the towers, based on the initial

examination in Problem 1.9 (p. 28).

1. Perform a diagnostic analysis of the linear regression model ﬁtted in Prob-

lem 2.18 (p. 88), and show a transformation of the response is necessary.

2. Fit an appropriate linear regression model to the data after applying the

transformation, ensuring a diagnostic analysis.

3.17. In Problem 2.17, the daily energy requirements and weight of 64

wethers (Table 2.11; data set: sheep) were analysed [18, 38, 42].

1. Using the model ﬁtted in Problem 2.17, perform a diagnostic analysis.

2. Fit another linear regression model using the logarithm of energy re-

quirements as the response variable. Perform a diagnostic analysis of this

second model, and show this is a superior model.

3. Interpret the model that was ﬁtted using the logarithm of energy require-

ments.

154 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3 .10 Age, percent body fat and bmi (in kg/m

) for 18 normal adults aged

between 23 and 61 years, for males (M) and females (F) (Problem 3.18)

Age Percent Age Percent

(years) body fat Gender bmi (years) body fat Gender bmi

23 9.5 M 17.8 56 32.5 F 28.4

23 27.9 F 22.5 57 30.3 F 31.8

27 7.8 M 24.6 58 33.0 F 25.2

27 17.8 M 20.5 53 34.7 F 23.8

39 31.4 F 25.1 53 42.0 F 22.8

41 25.9 F 21.4 54 29.1 F 26.4

45 27.4 M 26.0 58 33.8 F 28.3

49 25.2 F 22.3 60 41.1 F 23.2

50 31.1 F 21.8 61 34.5 F 23.2

3.18. A study [23] measured the body fat percentage and bmi of adults aged

between 23 and 61 (Table 3.10; data set: humanfat).

1. Plot the data, distinguishing between males and females. Which assump-

tions, if any, appear to be violated?

2. Fit the linear regression model with systematic component Percent.Fat

~ Age * Gender to the data.

3. Write down the two systematic components corresponding to females and

males.

4. Interpret each coeﬃcient in this model.

5. Use a t-test to determine if the interaction term is signiﬁcant.

6. Use an F -test to determine if the interaction term is signiﬁcant.

7. Show that the P -values for the t-andF -tests are the same for the inter-

action term, and explain why. Also show that the square of the t-statistic

is the F -statistic (within the limitations of computer arithmetic).

8. To the earlier plot, add the separate regression lines for males and females.

9. Compute and plot the 90% conﬁdence intervals about the ﬁtted values

for both males and females, and comment

10. Argue that only using the females in the study is sensible. Furthermore,

argue that only using females aged over 38 is sensible.

11. Using this subset of the data, ﬁnd a model using age and bmi as explana-

tory variables.

12. Using this model, compute Cook’s distance, leverages, Studentized resid-

uals and standardized residuals to evaluate the model. Identify any out-

liers and inﬂuential observations, and discuss the diﬀerences between the

Studentized and standardized residuals.

3.19. A study of urethral length L and mass M of various mammals [41]

expected to ﬁnd isometric scaling; that is, proportional relationships being

maintained as the size of animals increases. For these data (Table 3.11; data

set: urinationL) then, one postulated relationship is L = kM

1/3

for some

3.17 Summary 155

Tabl e 3 .11 The urethral length of 47 mammals (Problem 3.19)

Mean mass Mean urethral Sample

Animal Sex (in kg) length (in mm) size

Mouse F 0.02 10.0 1

Wister rat F 0.20 9.5 20

Rat F 0.20 17.0 1

Sprague-Dawley rat F 0.30 20.0 61

Dunkin Hartley guinea pig M 0.40 20.0 1

Normal adult cat F 2.30 49.4 1

Tabl e 3 .1 2 The mean annual rainfall, altitude, latitude and longitude for 24 cities in

the wheat-growing region of eastern Australia. Only the ﬁrst six observations are shown

(Problem 3.20)

Station Altitude Latitude Longitude Mean annual

name (in m) (

◦

S) (

◦

E) rainfall (in mm) Region

Goondiwindi 216.0 28.53 150.30 529 3

Condobolin 199.0 33.08 147.15 447 1

Coonamble 180.0 30.97 148.38 505 1

Gilgandra 278.0 31.72 148.67 563 2

Nyngan 177.0 31.56 147.20 440 1

Trangie 219.0 32.03 147.99 518 1

proportionality constant k. By using a transformation, ﬁt an appropriate

weighted linear regression model, and test the hypothesis using both a t-test

and an F -test. Interpret your model.

3.20. A study of the annual rainfall between 1916 and 1990 in a wheat-

growing region of eastern Australia [6] explored the relationships between

mean annual rainfall AR and region Region, altitude Alt, latitude Lat and

longitude Lon (Table 3.12; data set: wheatrain).

1. Plot the annual rainfall against the region and altitude, and identify any

important features.

2. Interpret a regression model with systematic component AR ~ Alt *

Region.

3. Fit the model with systematic component AR ~ Alt * Region. Show

that the interaction term is not necessary in the model, but both main

eﬀect terms are necessary.

4. Produce diagnostic plots and evaluate the ﬁtted model. Use both stan-

dardized and Studentized residuals, and compare. Identify the observa-

tion that appears to be an outlier.

156 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3 . 13 The strength of Kraft paper measured for various percentages of hardwood

concentration (Problem 3.21)

Strength % Hardwood Strength % Hardwood Strength % Hardwood

6.3 1.0 33.8 5.0 52.0 10.0

11.1 1.5 34.0 5.5 52.5 11.0

20.0 2.0 38.1 6.0 48.0 12.0

24.0 3.0 39.9 6.5 42.8 13.0

26.1 4.0 42.0 7.0 27.8 14.0

30.0 4.5 46.1 8.0 21.9 15.0

53.1 9.0

5. The data are spatial, so examine the independence of the data by plotting

the residuals against Lon and against Lat. Comment.

6. Summarize the diagnostic analysis of the ﬁtted model.

3.21. The tensile strength of Kraft paper (a strong, coarse and usually brown-

ish type of paper) was measured [18, 19] for diﬀerent percentages of hardwood

concentrations (Table 3.13; data set: paper).

1. Plot the data, and show that the data have a non-linear relationship.

2. Determine a suitable polynomial model for the data using poly().

3. Determine a suitable model using a regression spline.

4. Plot the two models (one using poly(); one using a regression spline) on

the data, and comment.

3.22. An experiment was conducted [11] to measure the heat developed by

setting cement with varying constituents (Table 3.14; data set: setting).

1. Plot each explanatory variable against heat evolved, and decide which

constituents appear to be related to heat evolved.

2. Fit the linear regression model predicting heat evolved from the explana-

tory variables A, B, C and D (that is, no interactions). Using t-tests, deter-

mine which explanatory variables appear statistically signiﬁcant. Com-

pare to your decisions in the previous part of this question.

3. Show that collinearity may be a problem. Explain why this may be the

case, and propose a solution.

4. Fit the amended model, and compare the t-test results to the t-test results

from the initial model above.

3.23. A compilation of data [1] from various studies of Gopher tortoises linked

the mean clutch size to environmental variables for 19 populations of the

tortoises (Table 3.15; data set: gopher).

1. Plot the mean clutch size against the temperature and evapotranspira-

tion. Comment on the relationships.

3.17 Summary 157

Tabl e 3 . 14 The amount of heat evolved (in calories/gram of cement) Heat by setting

cement for given percentages of four constituents: A refers to tricalcium aluminate; B

to tricalcium silicate; C to tetracalcium alumino ferrite; D to dicalcium silicate (Prob-

lem 3.22)

A B C D Heat ABCDHeat A B C D Heat

7 26 6 60 78.5 11 55 9 22 109.2 21 47 4 26 115.9

1 29 15 52 74.3 3 71 17 6 102.7 1 40 23 34 83.8

11 56 8 20 104.3 1 31 22 44 72.5 11 66 9 12 113.3

11 31 8 47 87.6 2 54 18 22 93.1 10 68 8 12 109.4

7 52 6 33 95.9

Tabl e 3. 1 5 Results from 19 studies of Gopher tortoises. Lat is the latitude at which

the study was conducted; Evap is the mean total annual actual evapotranspiration (in

mm); Temp is the mean annual temperature (in

◦

C); ClutchSize is the mean clutch size;

SampleSize is the sample size used in the study (Problem 3.23)

Site Latitude Evap Temp ClutchSize SampleSize

1 26.8 1318 24.0 8.2 23

2 27.3 1193 22.2 6.5 8

3 27.7 1112 22.7 7.6 32

4 28.0 1171 22.6 7.1 19

5 28.5 1116 21.4 4.8 12

6 28.5 1116 21.4 5.8 16

7 28.5 1116 21.4 8.0 19

8 28.6 1198 22.2 7.5 24

9 29.5 1091 20.4 5.8 62

10 29.7 1091 20.4 5.8 51

11 30.3 1037 20.4 5.0 23

12 30.7 1039 20.0 4.6 11

13 30.8 1030 19.2 5.5 19

14 30.9 1036 19.3 7.0 47

15 31.2 995 19.2 5.6 36

16 31.3 992 18.8 4.8 87

17 31.9 1018 19.7 6.5 25

18 32.5 965 18.6 3.8 23

19 32.6 911 18.6 4.5 23

2. Explain why a weighted linear regression model is appropriate.

3. Fit a weighted linear regression model for modelling ClutchSize using

Evap and Temp as explanatory variables. Produce the t-tests, and com-

ment.

4. Compute the anova table for the ﬁtted model, and comment.

5. Show that collinearity is evident in the data.

6. Perform a diagnostic analysis of this model. Be sure to test spatial inde-

pendence by plotting the residuals against Latitude.

3.24. Consider the (artiﬁcial) data in Table 3.16 (based on [14]), and con-

tained in data set triangle.

158 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3 .16 The data for Problem 3.24

10.1 5.3 8.5 11.1 4.2 10.3 8.8 4.2 7.7 10.9 5.7 9.3

11.6 5.4 10.3 11.4 5.0 10.2 13.5 5.6 12.3 12.2 4.0 11.6

10.4 4.5 9.4 13.0 5.0 12.1 10.3 3.2 9.8 11.3 4.2 10.4

13.0 4.7 12.2 13.2 6.9 11.2 12.6 6.5 10.8 10.1 5.6 8.5

12.3 6.6 10.4 10.2 4.7 9.0 10.1 4.3 9.1 9.7 5.6 7.9

1. Fit the linear regression model with the systematic component y~x1+

x2 to the data. Show that the interaction term is not necessary.

2. Use appropriate diagnostics to show the model is appropriate.

3. Interpret the ﬁtted model.

4. The data are actually randomly generated so that μ =



+ x

; that

is, x

and x

are the lengths of the sides of a right-angled triangle, and

μ is the length of the hypotenuse (and some randomness has been added

to produce y). What lesson does this demonstrate?

5. Fit the model for modelling μ =E[y

], using the systematic component

I(x1^2) + I(x2^2) - 1. Then use the t-test to conﬁrm that the pa-

rameter estimates suggested by Pythagoras’ theorem are supported by

the data.

3.25. In an experiment [39, p 122] conducted to investigate the amount of

drug retained in the liver of a rat (Table 3.17; data set: ratliver), nineteen

rats were randomly selected, weighed, and placed under light anesthetic and

given an oral dose of the drug. Because large livers were thought to absorb

more of a given dose than a small liver, the dose was approximately deter-

mined as 40 mg of the drug per kg of body weight. After a ﬁxed length of

time, each rat was sacriﬁced, the liver weighed, and the percentage dose in

the liver y determined.

1. Plot DoseInLiver against each explanatory variable, and identify impor-

tant features to be modelled.

2. Fit a linear regression model with systematic component DoseInLiver ~

BodyWt + LiverWt + Dose.

3. Using t-tests, show that BodyWt and Dose are signiﬁcant for modelling

DoseInLiver.

4. In the study, the dose was determined as an approximate function of

body weight, hence both variables BodyWt and Dose measure almost the

same physical quantity. Why should both covariates be necessary in the

model? By computing the appropriate statistics, show that Observation 3

has high leverage and is inﬂuential.

5. Plot BodyWt against Dose, and identify Observation 3 to see the problem.

6. Fit the same linear regression model, after omitting Observation 3. Use

t-tests to show that none of the covariates are now statistically signiﬁcant.

3.17 Summary 159

Tabl e 3 .1 7 Drug doses retained in the liver of rats. See the text for an explanation of

the data. BodyWt is the body weight of each rat (in g); LiverWt is liver weight (in g);

Dose is the dose relative to largest dose; DoseInLiver is the proportion of the dose in

liver, as percentage of liver weight (Problem 3.25)

BodyWt LiverWt Dose DoseInLiver BodyWt LiverWt Dose DoseInLiver

176 6.50.88 0.42 158 6.90.80 0.27

176 9.50.88 0.25 148 7.30.74 0.36

190 9.01.00 0.56 149 5.20.75 0.21

176 8.90.88 0.23 163 8.40.81 0.28

200 7.21.00 0.23 170 7.20.85 0.34

167 8.90.83 0.32 186 6.80.94 0.28

188 8.00.94 0.37 146 7.30.73 0.30

195 10.00.98 0.41 181 9.00.

90 0.37

176 8.00.88 0.33 149 6.40.75 0.46

165 7.90.84 0.38

Tabl e 3. 18 Inorganic and organic phosphorus in 18 soil samples, tested at 20

◦

C. Inorg

is the amount of inorganic phosphorus (in ppm); Org is the amount of organic phosphorus

(in ppm); PA is the amount of plant-available phosphorus (in ppm) (Problem 3.26)

Sample Inorg Org PA Sample Inorg Org PA Sample Inorg Org PA

1 0.4 53 64 7 9.4 44 81 13 23.1 50 77

2 0.4 23 60 8 10.1 31 93 14 21.6 44 93

3 3.1 19 71 9 11.6 29 93 15 23.1 56 95

4 0.6 34 61 10 12.6 58 51 16 1.9 36 54

5 4.7 24 54 11 10.9 37 76 17 26.8 58 168

6 1.7 65 77 12 23.1 46 96 18 29.9 51 99

3.26. The amount of organic, inorganic and plant-available phosphorus was

chemically determined [35] in eighteen soil samples (Table 3.18; data set:

phosphorus), all tested at 20

◦

1. Plot the plant-available phosphorous against both inorganic and organic

phosphorus. Comment.

2. Fit the linear regression model with systematic component PA ~ Inorg

+ Org.

3. Use t-tests to identify which covariates are statistically signiﬁcant.

4. Use appropriate statistics to identify any inﬂuential observations, and

any observations with high leverage.

3.27. Thirteen American footballers punted a football [26], and had their leg

strengths measured (Table 3.19; data set: punting).

1. Plot punting distance y against left leg strength x

, and then against

right leg strength x

. Comment.

2. Show that collinearity is likely to be a problem.

3. Propose a sensible solution to the collinearity problem.

160 3 Linear Regression Models: Diagnostics and Model-Building

Tabl e 3.1 9 Leg strength (in lb) and punting distance (in feet, using the right foot)

for 13 American footballers. Leg strengths were determined using a weight lifting test

(Problem 3.27)

Left-leg Right-leg Punting Left-leg Right-leg Punting

strength strength distance strength strength distance

170 170 162.50 110 110 104.83

130 140 144.00 110 120 105.67

170 180 174.50 120 130 117.58

160 160 163.50 140 120 140.25

150 170 192.00 130 140 150.17

150 150 171.75 150 160 165.17

180 170 162.00

Tabl e 3.2 0 The age and salary (including bonuses) of ceos of small companies. The

ﬁrst six observations are shown (Problem 3.28)

Age Salary

(in years) (in $’000)

53 145

43 621

33 262

45 208

46 362

55 424

4. Determine a suitable model for the data, ensuring a diagnostics analysis.

5. Interpret the ﬁnal model.

3.28. The age and salary of the chief executive oﬃcers (ceo) of small com-

panies in 1993 (Table 3.20; data set: ceo) were published by Forbes maga-

zine [34]. (Small companies were deﬁned as those with annual sales greater

than $5 million and less than $350 million, according to 5-year average return

on investment.) Find a suitable model for the data, and supply appropriate

diagnostics to show the model is appropriate.

3.29. A study of computer tomography (ct) interventions [32, 43]inthe

abdomen measured the total procedure time and the total radiation dose

received (Table 3.21; data set: fluoro). During these procedures, “one might

postulate that the radiation dose received is related to. . . the total procedure

time” [43, p. 619].

1. Plot the dose against the exposure time, and comment.

2. Fit the linear regression model for modelling dose from exposure time.

Produce the residual plots, and show that the variance is not constant.

3.17 Summary 161

Tabl e 3 . 21 Total exposure time and radiation dose for nineteen patients undergoing

ct ﬂuoroscopy in the abdomen (Problem 11.13)

Time Dose Time Dose Time Dose

(in min) (in rad) (in min) (in rad) (in min) (in rad)

37 4.39 66 9.39 90 34.81

48 3.46 67 6.36 92 16.61

52 8.00 75 17.12 97 58.56

57 5.47 75 50.91 98 84.77

58 8.00 83 20.70 100 23.57

61 18.92 83 25.28 114 66.02

86 47.94

Tabl e 3 . 22 Percentage butterfat for various pure-bred cattle taken from Canadian

records. There are ﬁve breeds, and ten 2-year old cows have been randomly selected plus

ten mature (older than 4 years) cows (Problem 3.30)

Ayrshire Canadian Guernsey Holstein–Fresian Jersey

Mature 2 years Mature 2 years Mature 2 years Mature 2 years Mature 2 years

3.74 4.44 3.92 4.29 4.54 5.30 3.40 3.79 4.80 5.75

4.01 4.37 4.95 5.24 5.18 4.50 3.55 3.66 6.45 5.14

3.77 4.25 4.47 4.43 5.75 4.59 3.83 3.58 5.18 5.25

3.78 3.71 4.28 4.00 5.04 5.04 3.95 3.38 4.49 4.76

4.10 4.08 4.07 4.62 4.64 4.83 4.43 3.71 5

.24 5.18

4.06 3.90 4.10 4.29 4.79 4.55 3.70 3.94 5.70 4.22

4.27 4.41 4.38 4.85 4.72 4.97 3.30 3.59 5.41 5.98

3.94 4.11 3.98 4.66 3.88 5.38 3.93 3.55 4.77 4.85

4.11 4.37 4.46 4.40 5.28 5.39 3.58 3.55 5.18 6.55

4.25 3.53 5.05 4.33 4.66 5.97 3

.54 3.43 5.23 5.72

3. Try using various transformations of the response variable. Fit these

model, and re-examine the residual plots to determine a suitable trans-

formation.

4. Test the hypothesis implied by the quote given original article.

5. Interpret the ﬁnal model.

3.30. The average butterfat content of milk from dairy cows was recorded

for each of ﬁve breeds of cattle [18, 36]. Random samples of ten mature

(older than 4 years) and ten 2-year olds were taken (Table 3.22; data set:

butterfat).

1. Plot the percentage butterfat against breed, and also against age. Discuss

any features of the data that are apparent.

2. Use various transformation to make the variance of the response approxi-

mately constant. Which transformation appears appropriate? Does using

boxcox() help with the decision?

3. Fit an appropriate linear regression model, and interpret the appropriate

diagnostics.

162 REFERENCES

References

[1] Ashton, K.G., Burke, R.L., Layne, J.N.: Geographic variation in body

and clutch size of Gopher tortoises. Copeia 2007(2), 355–363 (2007)

[2] Atkinson, A.C.: Regression diagnostics, transformations and constructed

variables. Journal of the Royal Statistical Society, Series B 44(1), 1–36

(1982)

[3] Belsley, D.A., Kuh, E., Welsch, R.E.: Regression Diagnostics: Identifying

Inﬂuential Data and Sources of Collinearity. John Wiley & Sons, New

York (2004)

[4] Benson, J.: Season of birth and onset of locomotion: Theoretical and

methodological implications. Infant Behavior and Development 16(1),

69–81 (1993)

[5] Bivand, R.S., Pebesma, E.J., Gómez-Rubio, V.: Applied Spatial Data

Analysis with r. Springer (2008)

[6] Boer, R., Fletcher, D.J., Campbell, L.C.: Rainfall patterns in a major

wheat-growing region of Australia. Australian Journal of Agricultural

Research 44, 609–624 (1993)

[7] Box, G.E.P., Cox, D.R.: An analysis of transformations (with discus-

sion). Journal of the Royal Statistical Society, Series B 26, 211–252

(1964)

[8] Cochran, D., Orcutt, G.H.: Application of least squares regression to re-

lationships containing auto-correlated error terms. Journal of the Amer-

ican Statistical Association 44(245), 32–61 (1949)

[9] Cook, D.R.: Detection of inﬂuential observations in linear regression.

Technometrics 19(1), 15–18 (1977)

[10] Davison, A.C.: Statistical Models. Cambridge University Press, UK

(2003)

[11] Draper, N., Smith, H.: Applied Regression Analysis. John Wiley and

Sons, New York (1966)

[12] Fox, J.: An R and S-Plus Companion to Applied Regression Analysis.

Sage Publications, Thousand Oaks, CA (2002)

[13] Geary, R.C.: Testing for normality. Biometrics 34(3/4), 209–242 (1947)

[14] Gelman, A., Nolan, D.: Teaching Statistics: A Bag of Tricks. Oxford

University Press, Oxford (2002)

[15] Gethin, G.T., Cowman, S., Conroy, R.M.: The impact of Manuka honey

dressings on the surface pH of chronic wounds. International Wound

Journal 5(2), 185–194 (2008)

[16] Gethin, G.T., Cowman, S., Conroy, R.M.: Retraction: The impact of

Manuka honey dressings on the surface pH of chronic wounds. Interna-

tional Wound Journal 11(3), 342–342 (2014)

REFERENCES 163

[17] Giauque, W.F., Wiebe, R.: The heat capacity of hydrogen bromide from

◦

K. to its boiling point and its heat of vaporization. The entropy from

spectroscopic data. Journal of the American Chemical Society 51(5),

1441–1449 (1929)

[18] Hand, D.J., Daly, F., Lunn, A.D., McConway, K.Y., Ostrowski, E.: A

Handbook of Small Data Sets. Chapman and Hall, London (1996)

[19] Joglekar, G., Scheunemyer, J.H., LaRiccia, V.: Lack-of-ﬁt testing when

replicates are not available. The American Statistician 43, 135–143

(1989)

[20] Johnson, B., Courtney, D.M.: Tower building. Child Development 2(2),

161–162 (1931)

[21] Kahn, M.: An exhalent problem for teaching statistics. Journal of Sta-

tistical Education 13(2) (2005).

[22] Little, R.J.A., Rubin, D.B.: Statistical analysis with missing data (2nd

ed.). Wiley, New York (2002)

[23] Mazess, R.B., Peppler, W.W., Gibbons, M.: Total body composition

by dualphoton (

153

Gd) absorptiometry. American Journal of Clinical

Nutrition 40, 834–839 (1984)

[24] Moir, R.J.: A note on the relationship between the digestible dry matter

and the digestable energy content of ruminant diets. Australian Journal

of Experimental Agriculture and Animal Husbandry 1, 24–26 (1961)

[25] Moore, D.S., McCabe, G.P.: Introduction to the Practice of Statistics,

second edn. W. H. Freeman and Company, New York (1993)

[26] Myers, R.H.: Classical and Modern Regression with Applications, second

edn. Duxbury, Belmont CA (1990)

[27] Palomares, M.L., Pauly, D.: A multiple regression model for predicting

the food consumption of marine ﬁsh populations. Australian Journal of

Marine and Freshwater Research 40(3), 259–284 (1989)

[28] Ryan, T.A., Joiner, B.L., Ryan, B.F.: Minitab Student Handbook.

Duxbury Press, North Scituate, Mass. (1976)

[29] Searle, S.R., Casella, G., McCulloch, C.E.: Variance Components. John

Wiley and Sons, New York (2006)

[30] Seddigh, M., Joliﬀ, G.D.: Light intensity eﬀects on meadowfoam growth

and ﬂowering. Crop Science 34, 497–503 (1994)

[31] Shacham, M., Brauner, N.: Minimizing the eﬀects of collinearity in poly-

nomial regression. Industrial and Engineering Chemical Research 36,

4405–4412 (1997)

[32] Silverman, S.G., Tuncali, K., Adams, D.F., Nawfel, R.D., Zou, K.H.,

Judy, P.F.: ct ﬂuoroscopy-guided abdominal interventions: Techniques,

results, and radiation exposure. Radiology 212, 673–681 (1999)

[33] Singer, J.D., Willett, J.B.: Improving the teaching of applied statistics:

Putting the data back into data analysis. The American Statistician

44(3), 223–230 (1990)

164 REFERENCES

[34] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011). URL

http://www.statsci.org/data

[35] Snapinn, S.M., Small, R.D.: Tests of signiﬁcance using regression models

for ordered categorical data. Biometrics 42, 583–592 (1986)

[36] Sokal, R.R., Rohlf, F.J.: Biometry: The Principles and Practice of Statis-

tics in Biological Research, third edn. W. H. Freeman and Company,

New York (1995)

[37] Student: The probable error of a mean. Biometrika 6(1), 1–25 (1908)

[38] Wallach, D., Goﬃnet, B.: Mean square error of prediction in models for

studying ecological systems and agronomic systems. Biometrics 43(3),

561–573 (1987)

[39] Weisberg, S.: Applied Linear Regression. Wiley Series in Probability

and Mathematical Statistics. John Wiley and Sons, New York (1985)

[40] West, B.T., Welch, K.B., Galecki, A.T.: Linear Mixed Models: A Prac-

tical Guide using Statistical Software. CRC, Boca Raton, Fl (2007)

[41] Yang, P.J., Pham, J., Choo, J., Hu, D.L.: Duration of urination does not

change with body size. Proceedings of the National Academy of Sciences

111(33), 11 932–11 937 (2014)

[42] Young, B.A., Corbett, J.L.: Maintenance energy requirement of grazing

sheep in relation to herbage availability. Australian Journal of Agricul-

tural Research 23(1), 57–76 (1972)

[43] Zou, K.H., Tuncali, K., Silverman, S.G.: Correlation and simple linear

regression. Radiology 227, 617–628 (2003)

Chapter 4

Beyond Linear Regression: The

Method of Maximum Likelihood

Just as the ability to devise simple but evocative models is

the signature of the great scientist so overelaboration and

overparameterization is often the mark of mediocrity.

Box [2, p. 792]

4.1 Introduction and Overview

The linear regression model introduced in Chap. 2 assumes the variance is

constant, possibly from a normal distribution. Many data types exist for

which the randomness is not constant, and so other methods are necessary.

This chapter demonstrates situations where the linear regression model fails.

In these cases, least-squares estimation, as used in Chap. 2, is no longer ap-

propriate. Instead, maximum likelihood estimation is appropriate. In Chap. 4,

we discuss three speciﬁc situations in which linear regression models fail

(Sect. 4.2) and then consider a general approach to modelling such data

(Sect. 4.3). To ﬁt these models, maximum likelihood estimation is needed

and is reviewed in Sect. 4.4. We then examine maximum likelihood estima-

tion in the case of one parameter (Sect. 4.5) and more than one parameter

(Sect. 4.6), and then using matrix algebra (Sect. 4.7). Fitting models using

maximum likelihood is discussed in Sect. 4.8, followed by a review of the

properties of maximum likelihood estimators (Sect. 4.9). Results concerning

hypothesis tests (Sect. 4.10) and conﬁdence intervals (Sect. 4.11) are then pre-

sented, followed by a discussion of comparing non-nested models (Sect. 4.12).

4.2 The Need for Non-normal Regression Models

4.2.1 When Linear Models Are a Poor Choice

The random component of the regression models in Chap. 2 has constant

variance, possibly from a normal distribution. Three common situations exist

where the variation is not constant, and so linear regression models are a poor

choice for modelling such data:

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_4

165

166 4 Beyond Linear Regression: The Method of Maximum Likelihood

1. The response is a proportion, ranging between 0 and 1 inclusive, of a

total number of counts. As the modelled proportion approaches these

boundaries of 0 and 1, the variance of the responses must approach zero.

The variance must be smaller near 0 and 1 than the variation of pro-

portions near 0.5 (where the observations can spread equally in both

directions toward the boundaries). Thus, the variance is not, and can-

not be, constant. Furthermore, because the response is between 0 and 1,

the randomness cannot be normally distributed. For proportions of a

total number of counts, the binomial distribution may be appropriate

(Sect. 4.2.2; Chap. 9).

A speciﬁc example of binomial data is binary data (Example 4.6) where

the response takes one of two outcomes (such as ‘success’ and ‘failure’,

or ‘present’ and ‘absent’).

2. The response is a count. As the modelled count approaches zero, the

variance of the responses must approach zero. Furthermore, the normal

distribution is a poor choice for modelling the randomness because counts

are discrete and non-negative. For count data, the Poisson distribution

may be appropriate (Example 1.5; Sect. 4.2.3; Chap. 10).

3. The response is positive continuous. As the modelled response approaches

zero, the variance of the responses must approach zero. Furthermore,

the normal distribution is a poor choice because positive continuous

data are often right skewed, and because the normal distribution per-

mits negative values. For positive continuous data, distributions such

as the gamma and inverse Gaussian distributions may be appropriate

(Sect. 4.2.4; Chap. 11).

In these circumstances, the relationship between y and the explanatory vari-

ables is usually non-linear also: the response has boundaries in all cases, so

a linear relationship cannot apply for all values of the response.

4.2.2 Binary Outcomes and Binomial Counts

First consider binary regression. There are many applications in which the

response is a binary variable, taking on only two possible states. In this

situation, a transformation to normality is out of the question.

Example 4.1. (Data set: gforces) Military pilots sometimes black out when

their brains are deprived of oxygen due to G-forces during violent manoeu-

vres. A study [7] produced similar symptoms by exposing volunteers’ lower

bodies to negative air pressure, likewise decreasing oxygen to the brain. The

data record the ages of eight volunteers and whether they showed synco-

pal blackout-related signs (pallor, sweating, slow heartbeat, unconsciousness)

during an 18 min period. Does resistance to blackout decrease with age?

4.2 The Need for Non-normal Regression Models 167

> data(gforces); gforces

Subject Age Signs

1JW390

2JM421

3DT200

4LK371

5JK201

6MK210

7FP411

8DG521

The explanatory variable is Age. The response variable is Signs, coded as 1

if the subject showed blackout-related signs and 0 otherwise. The response

variable is binary, taking only two distinct values, and no transformation can

change that. A regression approach that directly models the probability of a

blackout response given the age of the subject is needed. 

The same principles apply to situations where a number of binary out-

comes are tabulated to make a binomial random variable, as in the following

example.

Example 4.2. (Data set: shuttles) After the explosion of the space shuttle

Challenger on January 28, 1986, a study was conducted [3, 4] to determine

if previously-collected data about the ambient air temperature at the time of

launch could have been used to foresee potential problems with the launch

(Table 4.1). In this example, the response variable is the number of damaged

O-rings out of six for each of the previous 23 launches with data available, so

only seven values are possible for the response. No transformation can change

this.

A more sensible model would be to use a binomial distribution with mean

proportion μ for modelling the proportion y of O-rings damaged out of m

at various temperatures x.(Here,m = 6 for every launch.) Furthermore,

a linear relationship between temperature and the proportion of damaged

O-rings cannot be linear, as proportions are restricted to the range (0, 1).

Instead, a systematic relationship of the form

log

1 − μ

= β

+ β

may be more suitable, since log{μ/(1 − μ)} has a range over the entire real

line. 

Combining the systematic and random components, a possible model for

the data is:



ym ∼ Bin(μ, m) (random component)

log

1 − μ

= β

+ β

x (systematic component).

(4.1)

168 4 Beyond Linear Regression: The Method of Maximum Likelihood

Tabl e 4. 1 The ambient temperature and the number of O-rings (out of six) damaged

for 23 of the 24 space shuttle launches before the launch of Challenger; Challenger was

the 25th shuttle. One engine was lost at sea and so its O-rings could not be examined

(Example 4.2)

Temperature O-rings Temperature O-rings Temperature O-rings

(in

◦

F) damaged (in

◦

F) damaged (in

◦

F) damaged

53 2 68 0 75 0

57 1 69 0 75 2

58 1 70 0 76 0

63 1 70 0 76 0

66 0 70 1 78 0

67 0 70 1 79 0

67 0 72 0 81 0

67 0 73 0

4.2.3 Unrestricted Counts: Poisson or Negative

Binomial

Count data is another situation where linear regression models are

inadequate.

Example 4.3. (Data set: nminer) A study [9] of the habitats of the noisy

miner (a small but aggressive native Australian bird) counted the number

of noisy miners y and the number of eucalypt trees x in two-hectare buloke

woodland transects (Table 1.2,p.15). Buloke woodland patches with more

eucalypts tend to have more noisy miners (Fig. 1.4,p.15).

The number of noisy miners is more variable where more eucalypts are

present. Between 0 and 10 eucalypts, the number of noisy miners is almost

always zero; between 10 and 20 eucalypts, the number of noisy miners in-

creases. This shows that the systematic relationship between the number of

eucalypts and the number of noisy miners is not linear. A possible model for

the systematic component is log μ = β

+β

x, where x is the number of euca-

lypt trees at a given site, and μ is the expected number of noisy miners. Using

the logarithm ensures μ>0 even when β

and β

range between −∞ and

∞, and also models the non-linear form of the relationship between μ and x.

Between 0 and 10 eucalypts, the number of noisy miners varies little. Be-

tween 10 and 20 eucalypts, a larger amount of variation exists in the number

of noisy miners. This shows that the randomness does not have constant

variance. Instead, the variation in the data may be modelled using a Poisson

distribution, y ∼ Pois(μ), where y =0, 1, 2,...,andμ>0.

Combining the systematic and random components, a possible model for

the data is:



y ∼ Pois(μ) (random component)

log μ = β

+ β

x (systematic component).

(4.2)



4.2 The Need for Non-normal Regression Models 169

Tabl e 4 .2 The time for delivery to soft drink vending machines (Example 4.4)

Time Cases Distance Time Cases Distance Time Cases Distance

(in mins) (in feet) (in mins) (in feet) (in mins) (in feet)

16.68 7 560 79.24 30 1460 19.00 7 132

11.50 3 220 21.50 5 605 9.50 3 36

12.03 3 340 40.33 16 688 35.10 17 770

14.88 4 80 21.00 10 215 17.90 10 140

13.75 6 150 13.50 4 255 52.32 26 810

18.11 7 330 19.75 6 462 18.75 9 450

8.00 2 110 24.00 9 448 19.83 8 635

17.83 7 210 29.00 10 776 10.75 4 150

15.35 6 200

4.2.4 Continuous Positive Observations

A third common situation where linear regressions are unsuitable is for pos-

itive continuous data.

Example 4.4. (Data set: sdrink) A soft drink bottler is analyzing vending

machine service routes in his distribution system [11, 13]. He is interested

in predicting the amount of time y required by the route driver to service

the vending machines in an outlet. This service activity includes stocking the

machine with beverage products and minor maintenance or housekeeping.

The industrial engineer responsible for the study has suggested that the two

most important variables aﬀecting the delivery time are the number of cases

of product stocked x

and the distance walked by the route driver x

.The

engineer has collected 25 observations on delivery time, the number of cases

and distance walked (Table 4.2).

In this case, the delivery times are strictly positive values. They are likely

to show an increasing mean–variance relationship with standard deviation

roughly proportional to the mean, so a log-transformation might be approx-

imately variance stabilizing. However the dependence of time on the two

covariates is likely to be directly linear, because time should increase linearly

with the number of cases or the distance walked (Fig. 4.1); that is, a sensible

systematic component is μ = β

+ β

. No normal linear regression

approach can achieve these conﬂicting aims, because any transformation to

stabilize the variance would destroy linearity. A regression approach that di-

rectly models the delivery times using an appropriate probability distribution

for positive numbers (such as a gamma distribution) is desirable. Combining

the systematic and random components, a possible model for the data is:



y ∼ Gamma(μ; φ) (random component)

μ = β

+ β

x (systematic component)

(4.3)

where φ is related to the variance of the gamma distribution. 

170 4 Beyond Linear Regression: The Method of Maximum Likelihood

0 5 10 15 20 25 30

Service time vs cases sold

Number of cases of product sold

Service time (in mins)

0 500 1000 1500

Service time vs distance waked

Distance walked by driver (in feet)

Service time (in mins)

Fig. 4.1 A plot of the soft drink data: time against the number of cases of product sold

(left panel) and time against the distance walked by the route driver (right panel)

Tabl e 4. 3 The time to death (in weeks) and white blood cell count (wbc) for leukaemia

patients, grouped according to ag type (Example 4.5)

ag positive patients ag negative patients

Time to Time to Time to Time to

wbc death wbc death wbc death wbc death

2300 65 7000 143 4400 56 28000 3

750 156 9400 56 3000 65 31000 8

4300 100 32000 26 4000 17 26000 4

2600 134 35000 22 1500 7 21000 3

6000 16 100000 1 9000 16 79000 30

10500 108 100000 1 5300 22 100000 4

10000 121 52000 5 10000 3 100000 43

17000 4 100000 65 19000 4 27000 2

5400 39

Example 4.5. (Data set: leukwbc) The times to death (in weeks) of two

groups of leukaemia patients (grouped according to a morphological vari-

able called the ag factor) were recorded (Table 4.3) and their white blood

cell counts were measured (Fig. 4.2). The authors originally ﬁtted a model

using the exponential distribution [5, 6].

We would like to model the survival times on a log-linear scale, building a

linear predictor for log μ

, where μ

> 0 is the expected survival time. How-

ever the log-survival times are not normally distributed, as the logarithm of

an exponentially distributed random variable is markedly left-skewed. Hence

normal linear regression with the log-survival times as response is less than

desirable. Furthermore, linear regression would estimate the variance of the

residuals, whereas the variance of an exponential random variable is known

once the mean is speciﬁed. An analysis that uses the exponential distribution

explicitly is needed. 

4.3 Generalizing the Normal Linear Model 171

0 20406080100

100

150

Time to death vs

white blood cell count

White blood cell count, in thousands

Time to death (in weeks)

AG positive

AG negative

Fig. 4.2 A plot of the leukaemia data: time to death against the white blood cell count

(Example 4.5)

Tabl e 4.4 Diﬀerent models discussed so far, all of which are generalized linear models.

In all cases η = β



j=1

for the appropriate explanatory variables x

(Sect. 4.3)

Random Systematic

Data Reference component component

fev data Example 1.1 (p. 1)Normal μ = η

Challenger data Example 4.2 (p. 167) Binomial log {μ/(1 − μ)} = η

Noisy miner data Example 4.3 (p. 168) Poisson log μ = η

Soft drink data Example 4.4 (p. 169) Gamma μ = η

Leukaemia data Example 4.5 (p. 170) Exponential log μ = η

4.3 Generalizing the Normal Linear Model

For the data in Sect. 4.2, diﬀerent models are suggested (Table 4.4): a variety

of random and systematic components appear. The theory in Chaps. 2 and 3,

based on linearity and constant variance, no longer applies.

To use each of the models listed in Table 4.4 requires the development

of separate theory: ﬁtting algorithms, inference procedures, diagnostic tools,

and so on. An alternative approach is to work more generally. For example,

later we consider a family of distributions which has the normal, binomial,

Poisson and gamma distributions as special cases. Using this general family

of distributions, any estimation algorithms, inference procedures and diag-

nostic tools that are developed apply to all distributions in this family of

distributions. Implementation for any one speciﬁc model would be a special

case of the general theory. In addition, later we allow systematic components

of the form f (μ)=η for certain functions f().

172 4 Beyond Linear Regression: The Method of Maximum Likelihood

This is the principle behind generalized linear models (glms). Glms unify

numerous models into one general theoretical framework, incorporating all

the models in Table 4.4 (and others) under one structure. Common estima-

tion algorithms (Chap. 6), inference methods (Chap. 7), and diagnostic tools

(Chap. 8) are possible under one common framework. The family of distri-

butions used for glms is called the exponential dispersion model (or edm)

family, which includes common distributions such as the normal, binomial,

Poisson and gamma distributions, among others.

Why should the random component be restricted to distributions in the

edm family? For example, distributions such as the Weibull distribution and

von Mises distribution are not edms, but may be useful for modelling certain

types of data. Glms are restricted to distributions in the edm family because

the general theory is developed by taking advantage of the structure of edms.

Using the structure provided by the edm family enables simple ﬁtting algo-

rithms and inference procedures, which share similarities with the normal

linear regression models. The theory does not apply to distributions that are

not edms. Naturally, if a non-edm distribution really is appropriate it should

be used (and the model will not be a glm). However, edms are useful for

most common types of data:

• Continuous data over the entire real line may be modelled by the normal

distribution (Chaps. 2 and 3).

• Proportions of a total number of counts may be modelled by the binomial

distribution (Example 4.2; Chap. 9).

• Discrete count data may be modelled by the Poisson or negative binomial

distributions (Example 4.3; Chap. 10).

• Continuous data over the positive real line may be modelled by the

gamma and inverse Gaussian distributions (Example 4.4; Chap. 11).

• Positive data with exact zeros may be modelled by a special case of the

Tweedie distributions (Chap. 12).

The advantages of glms are two-fold. Firstly, the mean–variance relation-

ship can be chosen separately from the appropriate scale for the linear predic-

tor. Secondly, by choosing a response distribution that matches the natural

support of the responses, we can expect to achieve a better approximation to

the probability distribution.

4.4 The Idea of Likelihood Estimation

Chapter 2 developed the principle of least-squares as a criterion for esti-

mating the parameters in the linear predictor of linear regression models.

Least-squares is an appropriate criterion for ﬁtting regression models to re-

sponse data that are approximately normally distributed. In the remainder of

this chapter, we develop a much more general estimation methodology called

4.4 The Idea of Likelihood Estimation 173

maximum likelihood. Maximum likelihood is appropriate for estimating the

parameters of non-normal models such as those based on the binomial, Pois-

son or gamma distributions discussed earlier in this chapter, and includes

least-squares as a special case. Maximum likelihood tools will be used exten-

sively for ﬁtting models and testing hypotheses in the remaining chapters of

this book.

Maximum likelihood can be applied whenever a speciﬁc probability distri-

bution has been proposed for the data at hand. The idea of maximum likeli-

hood is to choose those estimates for the unknown parameters that maximize

the probability density of the observed data.

Suppose for example that y

,...,y

are independent observations from

an exponential distribution with scale parameter θ. The probability density

function, or probability function, of the exponential distribution is

P(y; θ)=θ exp(−yθ).

The joint probability density function of y

,...,y

therefore is

P(y

,...,y

; θ)=



i=1

P(y

; θ)=θ

exp(−n¯yθ)

where ¯y is the arithmetic mean of the y

. This quantity is called the likelihood

function, L(θ; y

,...,y

). This is often written more compactly as L(θ; y), so

that

L(θ; y)=



i=1

P(y

; θ)=θ

exp(−n¯yθ).

The maximum likelihood principle is to estimate θ by that value

θ that

maximizes this joint probability function. The value of the parameter θ that

maximizes the likelihood function is the maximum likelihood estimate (mle)

of that parameter. In this book, mles will be represented by placing a ‘hat’

over the parameter estimated, so the mle of θ is denoted

θ. For the exponen-

tial distribution example above, it is easy to show that L(θ; y) is maximized

with respect to θ at 1/¯y (Problem 4.5). Hence we say that the maximum

likelihood estimator of θ is

θ =1/¯y.

Ordinarily, the probability function is viewed a function of y

,...,y

for

a given parameter θ. Likelihood theory reverses the roles of the observations

and the parameters, considering the probability function as a function of

the parameters for a given set of observations. In practice, the log-likelihood

function (θ; y

,...,y

), often written more compactly as (θ; y), is usually

more convenient to work with:

(θ; y) = log L(θ; y)=



i=1

log P(y

; θ).

174 4 Beyond Linear Regression: The Method of Maximum Likelihood

Obviously, maximizing the log-likelihood is equivalent to maximizing the like-

lihood itself. For the exponential distribution example discussed above, the

log-likelihood function for θ is

(θ; y)=n(log θ − ¯yθ).

It is easy to show that least squares is a special case of maximum like-

lihood. Consider a normal linear regression model, y

∼ N(μ

,σ

), with

= β

+ β

+ ···+ β

. The normal distribution has the probabil-

ity density function

P(y

; μ

,σ

√

2πσ

exp



−

− μ

)

2σ



Hence the log-probability density function for y

log P(y

; μ

,σ

)=−

log(2πσ

) −

2σ

− μ

)

The log-likelihood function for the unknown parameters is

(β

,...,β

,σ

; y)=−

log(2πσ

) −

2σ



i=1

− μ

)

= −

log(2πσ

) −

2σ

rss,

where rss is the sum of squares. The likelihood depends on β

,...,β

only

through the rss and so, for any ﬁxed value of σ

, the likelihood is maxi-

mized by minimizing the rss. Hence maximizing the likelihood with respect

to the regression coeﬃcients β

is the same as minimizing the sum of squares.

Hence maximum likelihood is the same as least-squares for normal regression

models.

Example 4.6. The total July rainfall (in millimetres) at Quilpie, Australia, has

been recorded (Table 4.5; data set: quilpie), together with the value of the

monthly mean southern oscillation index (soi). The soi is the standardized

diﬀerence between the air pressures at Darwin and Tahiti, and is known to

have relationships with rainfall in parts of Australia [10, 14]. Some Australian

farmers may delay planting crops until a certain amount of rain has fallen (a

‘rain threshold’) within a given time frame (a ‘rain window’) [12]. Accordingly,

we deﬁne the response variable y as

y =



1 if the total July rainfall exceeds 10 mm

0 otherwise.

(4.4)

The unknown parameter here is the probability that the rainfall exceeds

10 mm, which we will write as μ because E[y]=μ =Pr(y = 1). We will

4.4 The Idea of Likelihood Estimation 175

Tabl e 4.5 The total July rainfall (in millimetres) at Quilpie, and the corresponding

soi and soi phase. The ﬁrst six observations are shown (Example 4.6)

Rainfall Rainfall soi

i Year (in mm) exceeds 10 mm? soi phase

1 1921 38.4 Yes 2.72

2 1922 0.0 No 2.05

3 1923 0.0 No −10.73

4 1924 24.4 Yes 6.92

5 1925 0.0 No −12.53

6 1926 9.1 No −1.04

be interested in the relationship between μ and soi, but for the moment we

ignore the soi and consider all the observations as equivalent.

The probability function of y is deﬁned by Pr(y =1)=μ and Pr(y =0)=

1 − μ or, more compactly, by

P(y; μ)=μ

(1 − μ)

1−y

, (4.5)

for y = 0 or 1. This is known as a Bernoulli distribution with probability μ,

denoted Bern(μ). The r function dbinom() evaluates the probability function

for the binomial distribution, and when size=1 the binomial distribution

corresponds to the Bernoulli distribution. Evaluating the log-likelihood for a

few test values of μ shows that the mle of μ is near 0.5, and certainly between

0.4 and 0.6:

> data(quilpie); names(quilpie)

[1] "Year" "Rain" "SOI" "Phase" "Exceed" "y"

> mu <- c(0.2, 0.4, 0.5, 0.6, 0.8) # Candidate values to test

> ll <- rep(0, 5) # A place-holder for the log-likelihood values

> for (i in 1:5)

ll[i] <- sum( dbinom(quilpie$y, size=1, prob=mu[i], log=TRUE))

> data.frame(Mu=mu, LogLikelihood=ll)

Mu LogLikelihood

1 0.2 -63.69406

2 0.4 -48.92742

3 0.5 -47.13401

4 0.6 -48.11649

5 0.8 -60.92148

Figure 4.3 plots the likelihood and log-likelihood functions for a greater range

of μ values. Visually, the mle of μ appears to be just above 0.5. 

176 4 Beyond Linear Regression: The Method of Maximum Likelihood

Likelihood function

Likelihood

0.0 0.2 0.4 0.6 0.8 1.0

1 × 10

−21

2 × 10

−21

3 × 10

−21

0.0 0.2 0.4 0.6 0.8 1.0

−100

−90

−80

−70

−60

−50

Log−likelihood function

Log−likelihood

Fig. 4.3 The likelihood function (top panel) and the log-likelihood function (bottom

panel) for the Quilpie rainfall data. The solid dots correspond to the ﬁve test values.

The vertical line is at ˆμ =0.5147

4.5 Maximum Likelihood for Estimating One Parameter

4.5.1 Score Equations

A systematic approach to maximizing the log-likelihood is to use calculus,

ﬁnding that value of the parameter where the derivative of the log-likelihood

is zero. If there is a single parameter ζ, the derivative of the log-likelihood

is called the score function, denoted U(ζ)=d/dζ, and the equation to be

solved for

ζ is the score equation U(

ζ) = 0. When there are p



unknown

regression parameters, there are p



corresponding score equations.

In general in calculus, a stationary point of a function is not necessarily

the global maximum—it could be merely a local maximum or even a local

minimum. The log-likelihood functions considered in this book however are

always unimodal and continuously diﬀerentiable in the parameters, so the

score equations always yield the maximum likelihood estimators.

4.5 Maximum Likelihood for Estimating One Parameter 177

The score function has the important property that it has zero expectation,

E[U(ζ)] = 0, when evaluated at the true parameter value (Problem 4.3). It

follows that var[U (ζ)] = E[U(ζ)

Example 4.7. The log-probability function of the Bernoulli distribution (4.5)

log P(y; μ)=y log μ +(1− y) log(1 − μ), (4.6)

so that

d log P(y; μ)

dμ

y −μ

μ(1 − μ)

The log-likelihood function is

(μ; y)=



i=1

log μ +(1− y

) log(1 − μ).

Hence the score function is

U(μ)=

d(μ; y)

dμ



i=1

− μ

μ(1 − μ)



i=1

− nμ

μ(1 − μ)

n(¯y − μ)

μ(1 − μ)

, (4.7)

where ¯y =(1/n)



i=1

is the sample mean of the y

or, in other words, the

proportion of cases for which y = 1. Setting U(ˆμ) = 0 and solving produces

ˆμ =¯y (Fig. 4.3); that is, the mle of μ is the sample mean. In r:

> muhat <- mean(quilpie$y); muhat

[1] 0.5147059



4.5.2 Information: Observed and Expected

The previous section focused on the derivative of the log-likelihood. We now

focus on the second derivative, as a measure of how well determined the mle

is. For simplicity of notation, we assume a single parameter ζ for this section.

Write J(ζ)forminus the second derivative of the log-likelihood with re-

spect to ζ:

J(ζ)=−

(ζ; y)

dζ

= −

dU(ζ)

dζ

J(ζ) must be positive near the mle

ζ. If it is large, then U is changing rapidly

near the mle and the peak of the log-likelihood is very sharp and hence the

estimate is well-deﬁned. In this situation, changing the estimate of ζ by a

178 4 Beyond Linear Regression: The Method of Maximum Likelihood

0.3 0.4 0.5 0.6 0.7

−60

−55

−50

−45

Log−likelihood function

Log−likelihood

Fig. 4.4 A plot of the likelihood function for the Quilpie rainfall data (solid line), and a

hypothetical log-likelihood that contains more information (dashed line). In both cases,

the mle is the same (as shown by the thin vertical line). The log-likelihood function

is sharper with more information (dashed line), so that a small change in the estimate

causes larger changes in the value of the log-likelihood

small amount will substantially change the value of the log-likelihood. This

means that

ζ is a very precise estimate of ζ (Fig. 4.4). On the other hand, if

J(ζ) is close to zero, then the log-likelihood is relatively ﬂat around

ζ and

the peak is less deﬁned. This means that

ζ is not so well determined and is

a less precise estimator of ζ. All this shows that J(ζ) is a measure of the

precision of the estimate

ζ;thatis,J(ζ) measures how much information is

available for estimating ζ.

The expression J(ζ)=−dU(ζ)/dζ is called the observed information.We

also deﬁne the expected information I(ζ)=E[J(ζ)], also called Fisher infor-

mation. Whereas J(ζ) is a function of the observed data, I(ζ) is a property

of the model. It measures the average information that will be observed for

this parameter from this model and the speciﬁed parameter value.

The expected information I(ζ) has some advantages over the observed

information J(ζ). First, expected information is much simpler to evaluate

for the models that will be considered in this book. Second, J(ζ) can only be

guaranteed to be positive at ζ =

ζ, whereas I

(ζ) is positive for any parameter

value. Third, I(ζ) has a very neat relationship to the variance of the score

function and to that of the mle itself, as shown in the next section.

Example 4.8. We continue the example ﬁtting the Bernoulli distribution to

the quilpie data introduced in Example 4.6. The second derivative of the

log-probability function (for an individual observation) is

(μ; y)

dμ

dU(μ)

dμ

−μ(1 − μ) − (y − μ)(1 − 2μ)

(1 − μ)

4.5 Maximum Likelihood for Estimating One Parameter 179

and so the observed information for μ is

J(μ)=−

(μ; y)

dμ

= −



i=1

log P(y; μ)

dμ

= n

μ(1 − μ) − (ˆμ − μ)(1 − 2μ)

(1 − μ)

When we evaluate at μ =ˆμ, the second term in the numerator is zero, so

that

J(ˆμ)=

ˆμ(1 − ˆμ)

Note that J(ˆμ) is positive, conﬁrming that the second derivative is negative

and hence that the log-likelihood has a maximum at ˆμ. In fact, ˆμ is a global

maximum of the likelihood. The expected information is

I(μ)=E[J(μ)] =

μ(1 − μ)

(4.8)

because E[ˆμ]=μ. Hence the observed and expected information coincide

when μ is evaluated at μ =ˆμ. Note that the expected information increases

proportionally with the sample size n. Evaluating (4.8)inr gives Fisher

information:

> n <- length( quilpie$y )

> Info <- n / (muhat *(1-muhat))

> c(muhat=muhat, FisherInfo=Info)

muhat FisherInfo

0.5147059 272.2354978



4.5.3 Standard Errors of Parameters

It can be shown that I(ζ)=E[U(ζ)] = var[U(ζ)] (Problem 4.3). This states

exactly how the expected information measures the rate of change in the

score function around the true parameter value. A Taylor’s series expansion

of the log-likelihood around ζ =

ζ shows furthermore that

var[

ζ] ≈ 1/I(ζ). (4.9)

Hence the expected information is a measure of the precision of the mle;

speciﬁcally, the variance of the mle is inversely proportion to the Fisher

information for the parameter. The estimated standard deviation (standard

error) of

ζ is 1/I(

ζ)

1/2

180 4 Beyond Linear Regression: The Method of Maximum Likelihood

Example 4.9. Based on the Fisher information found in Example 4.8,the

estimated standard error for ˆμ can be found:

> 1/sqrt(Info)

[1] 0.06060767



4.6 Maximum Likelihood for More Than One Parameter

4.6.1 Score Equations

Our discussion of likelihood functions so far has not included covariates and

explanatory variables. The normal and non-normal regression models devel-

oped in this book will assume that each response observation y

follows a

probability distribution that is parametrised by a location parameter μ

,ac-

tually the mean μ

=E[y

], and dispersion parameter φ that speciﬁes the

variance of y

. The mean μ

will be assumed to be a function of explana-

tory variables x

and regression parameters β

. Speciﬁcally, we will assume

a linear predictor

= β

+ β

+ ···+ β

The mean μ

depends on the linear predictor; more precisely, g(μ

)=η

for some known function g(). The function g() links the means to the linear

predictor, and so is known as the link function.

For regression models, the log-likelihood function is

(β

,β

,...,β

; y)=



i=1

log P(y

; μ

,φ).

The score functions have the form

U(β

∂(β

,β

,...,β

; y)

∂β



i=1

P(y

; μ

,φ)

∂μ

∂β

with one score function corresponding to each unknown regression parameter

Example 4.10. (Data set: quilpie) We return to the Quilpie rainfall example

(Example 4.6,p.174), now relating the soi to the probability that the rainfall

exceeds the 10 mm threshold. Plots of the data suggest that the probability

of exceeding 10 mm increases with increasing values of the soi (Fig. 4.5):

> boxplot( SOI ~ Exceed, horizontal=TRUE, data=quilpie, las=2,

xlab="July average SOI", ylab="Rainfall exceeds threshold" )

4.6 Maximum Likelihood for More Than One Parameter 181

lll

Yes

−20

−10

July average SOI

Rainfall exceeds threshold

July average SOI

Rainfall exceeds threshold

−20

−10

Yes

July average SOI

Rainfall exceeds threshold

−20 0 10

No Yes

0.0

0.2

0.4

0.6

0.8

1.0

Fig. 4.5 The relationship between the SOI and exceeding the rainfall threshold of

10 mm in July at Quilpie and the soi (Example 4.6)

> plot( jitter(y, 0.15) ~ SOI, data=quilpie, pch=19, axes=FALSE, las=2,

xlab="July average SOI", ylab="Rainfall exceeds threshold" )

> axis(side=1, las=2)

> axis(side=2, at=0:1, labels=c("No", "Yes"), las=2); box()

> cdplot( Exceed ~ SOI, data=quilpie,

xlab="July average SOI", ylab="Rainfall exceeds threshold" )

The left panel of Fig. 4.5 shows the distribution of the soi in years when

the rainfall exceeded and did not exceed the threshold. The centre panel of

Fig. 4.5 uses the jitter() command to add a small amount of randomness

to y to avoid overplotting. The right panel using a conditional density plot

for the data.

Recall that μ =Pr(y = 1) is the probability that the 10 mm threshold is

exceeded. A direct linear model would assume

μ = β

+ β

x. (4.10)

This, however, is not sensible for the Quilpie rainfall data. Since μ is a prob-

ability, it cannot be smaller than 0, nor larger than 1. The systematic com-

ponent (4.10) cannot ensure this without imposing diﬃcult-to-enforce con-

straints on the β

. A diﬀerent form of the systematic component is needed

to ensure μ remains between 0 and 1.

One possible systematic component is

log

1 − μ

= η = β

+ β

x, (4.11)

which ensures 0 <μ<1. The systematic component (4.11) has two parame-

ters to be estimated, β

and β

, so there are two score functions: U(β

)and

U(β

). Note that, from (4.11),

∂μ

∂β

= μ(1 − μ)and

∂μ

∂β

= μ(1 − μ)x.

182 4 Beyond Linear Regression: The Method of Maximum Likelihood

Then, working with just one observation, the score functions are

U(β

∂ log P(y; μ)

∂β

d log P(y; μ)

dμ

∂μ

∂β

= y −μ;

U(β

∂ log P(y; μ)

d log P(y; μ)

dμ

∂μ

∂β

=(y −μ)x.

Hence the two score equations are



i=1

− ˆμ

=0 and



i=1

− ˆμ

=0,

where log{ˆμ

/(1 − ˆμ

)} =

. Solving these simultaneous equations

for

and

is, in general, best achieved using iterative matrix algorithms

(Sect. 4.8). 

4.6.2 Information: Observed and Expected

The second derivatives of the log-likelihood, as seen earlier (Sect. 4.5.2), quan-

tify the amount of information available for estimating parameters. For more

than one parameter to be estimated, the second derivatives are

(β)=−

U(β

)

∂β

= −

dU(β

)

dμ

∂μ

∂β

The expected information is, as always, I

(β)=E[J

(β)]. Note that the

expected information relating to regression parameter β

is I

(β).

Example 4.11. Returning again to the Quilpie rainfall data (Example 4.6,

p. 174), we can compute:

(β)=−

∂U(β

)

∂β

= −

dU(β

)

dμ

∂μ

∂β



i=1

(1 − μ

);

(β)=−

∂U(β

)

∂β

= −

dU(β

)

dμ

∂μ

∂β



i=1

(1 − μ

;

(β)=J

(β)=−

∂U(β

)

∂β

= −

dU(β

)

dμ

∂μ

∂β



i=1

(1 − μ



4.7 Maximum Likelihood Using Matrix Algebra 183

4.6.3 Standard Errors of Parameters

Similar to before,

var[

] ≈ 1/I

(β),

so that the standard errors are se(

) ≈ 1/I

(

β)

1/2

* 4.7 Maximum Likelihood Using Matrix Algebra

* 4.7.1 Notation

Now assume that the responses come from a probability distribution with

probability function P(y; ζ), where ζ =[ζ

,...,ζ

] is a vector of unknown

parameters of the distribution. The likelihood function is the same as the

joint probability function, only viewed as a function of the parameters:

L(ζ

,...,ζ

; y

,...,y

)=L(ζ; y)=P(y; ζ). (4.12)

In practice, the log-likelihood function

(ζ; y ) = log L(ζ; y)

is usually more convenient to work with. Obviously, maximizing the log-

likelihood is equivalent to maximizing the likelihood itself.

The values of the parameters ζ

,...,ζ

that maximize the likelihood func-

tion are the maximum likelihood estimates (mle) of those parameters. In

this book, mles will be represented by placing a ‘hat’ over the parameter

estimated, so the mle of ζ is denoted

ζ =[

,...,

* 4.7.2 Score Equations

The ﬁrst derivative of the log-likelihood with respect to ζ is called the score

function or score vector U (ζ):

U(ζ)=

∂(ζ; y)

∂ζ



i=1

∂ log P(y

; ζ)

∂ζ

where U(ζ) is a vector of partial ﬁrst derivatives, one for each parameter in

ζ such that U(ζ

)=∂(ζ; y)/∂ζ

.Thus,themle of ζ is usually the unique

solution to the score equation

ζ)=0. (4.13)

184 4 Beyond Linear Regression: The Method of Maximum Likelihood

In some cases, several solutions exist to (4.13), or the log-likelihood may

be maximized at a boundary of the parameter space. In these cases, the log-

likelihood is evaluated at all solutions to (4.13) and the boundary values, and

the solution giving the maximum value is chosen. For all situations in this

book, a unique maximum occurs at the solution to (4.13), unless otherwise

noted. Solving (4.13) usually requires numerical methods (Sect. 4.8).

In the speciﬁc case of regression models, the parameter of interest is μ

which is usually a function of explanatory variables, so estimates of μ are

not of direct interest. For example, for the Quilpie rainfall data μ is assumed

to be some function of the soi x. In these situations, the estimates of the

regression parameters β

are of primary interest, so we need to evaluate the

derivatives of the log-likelihood with respect to the regression parameters.

For the models in this book, the linear predictor is written as

η = β

+ β

+ ···+ β

=Xβ

where X is an n × p



matrix, and β is a vector of regression parameters of

length p



. There will be p



score functions, one for each unknown parameter

, of the form:

U(β

∂(β; y)

∂β

d(β; y)

dμ

∂μ

∂β

Then, μ = g(η) for some known function g().

Simultaneously solving the score equations is not trivial in general, and

usually requires iterative numerical methods (Sect. 4.8).

Example 4.12. For the Quilpie rainfall example (data set: quilpie), the score

equations were given in Example 4.10 for estimating the relationship between

soi and the probability that rainfall exceeds the 10 mm threshold. In matrix

form, μ = g(η)=g (Xβ).

The mle

β =[

] is the solution to the score equation

β)=



i=1

− ˆμ



i=1

− ˆμ

= 0, (4.14)

where log{

μ/(1 −

μ)} =X

β. Solving this score equation is not trivial. 

* 4.7.3 Information: Observed and Expected

Under certain conditions, which hold for models in this book, the information

matrix (or the expected information matrix) I(ζ) is deﬁned as the negative

of the expected value of the matrix of second derivatives (Problem 4.3):

I(ζ)=−E



∂

(ζ; y )

∂ζ∂ζ



=E[J(ζ)].

4.7 Maximum Likelihood Using Matrix Algebra 185

J(ζ) is called the observed information matrix, where element (j, k) of this

matrix, denoted J

(ζ), is

(ζ)=−

∂

(ζ; y )

∂ζ

For the models in this book, η = β

+ β

+ ···+ β

=Xβ. Then, in

matrix form, the observed information for each parameter is

∂

(β; y )

∂β

dμ



∂(β; y)

∂β



∂μ

∂β

dU(β

)

dμ

∂μ

∂β

The mixed derivatives are

∂

(β; y )

∂β

∂

(β; y )

∂β

dμ



∂(β; y)

∂β



∂μ

∂β

dU(β

)

dμ

∂μ

∂β

These derivatives can be assembled into a matrix, called the observed in-

formation matrix, J(β). The expected information matrix (or Fisher infor-

mation matrix) is I(β)=E[J(β)]. When necessary, element (j, k)ofthe

information matrix is denoted I

(ζ).

Using these results, two important properties of the score vector (Prob-

lem 4.3)are:

1. The expected value of the score vector is zero: E[U (ζ)] = 0.

2. The variance of the score vector is var[U(ζ)] = I(ζ)=E[U(ζ)U (ζ)

Example 4.13. For the Quilpie rainfall example, expressions for the informa-

tion were given in Example 4.11. Using matrices and vectors, compute (for

example)

∂

(β; y)

∂β

dμ



∂(β; y)

∂β



∂μ

∂β

= −



i=1

(1 − μ

Computing all second derivatives (Problem 4.2), the 2 ×2 observed informa-

tion matrix J(β)is

J(β)=−

∂

(β; y)

∂β∂β





(1 − μ

)



(1 − μ



(1 − μ



(1 − μ



, (4.15)

where the summations are over i =1,...n,andμ

is deﬁned by (4.11). The

expected information matrix is

I(β)=E[J(β)] =





(1 − μ

)



(1 − μ



(1 − μ



(1 − μ



. (4.16)

For this example, the expected information I(β) and the observed informa-

tion matrix J(β) are identical, since J(β) does not contain any random

components. This is not true in general. 

186 4 Beyond Linear Regression: The Method of Maximum Likelihood

* 4.7.4 Standard Errors of Parameters

The variances of each parameter are found from the corresponding diagonal

elements of the inverse of the information matrix:

var[

] ≈I

−1

(β),

where I

−1

(β) is element (j, k)ofI

−1

(β). Hence, the standard error of each

parameter is

se(

) ≈I

−1/2

(

β).

If the oﬀ-diagonal elements of the information matrix are zero, then estimates

of the corresponding parameters, or sets of parameters, are independent and

can be computed separately.

Example 4.14. For the Bernoulli model ﬁtted to the Quilpie rainfall data, use

the information matrix in (4.16) to ﬁnd

−1

(

ζ)=





(1 − μ

−



(1 − μ

−



(1 − μ



(1 − μ

)



where Δ =



(1 − μ

)



(1 − μ

− (



(1 − μ

)

, and the sum-

mations are over i =1,...n. For example, the variance of

var[



i=1

(1 − μ

The standard error of

is the square root of var[

] after replacing μ with ˆμ.



* 4.8 Fisher Scoring for Computing MLEs

By deﬁnition, the mle occurs when U (

ζ)=0 (ignoring situations where the

maxima occur on the boundaries of the parameter space). Many methods

exist for solving such an equality. In general, an iterative technique is needed,

such as the Newton–Raphson method. In matrix form, the Newton–Raphson

iteration is

(r+1)

(r)

+ J(

(r)

)

−1

(r)

where

(r)

is the estimate of ζ at iteration r. In practice, the observed infor-

mation matrix J(ζ) may be diﬃcult to compute, so the expected (Fisher)

information matrix I(ζ)=E[J(ζ)] is used in place of the observed informa-

tion because I(ζ) usually has a simpler form than J(ζ). This leads to the

Fisher scoring iteration:

(r+1)

(r)

+ I(

(r)

)

−1

(r)

4.8 Fisher Scoring for Computing MLEs 187

Example 4.15. For the Quilpie rainfall data, the score vector is given in (4.14)

and the expected information matrix in (4.16). Solving the score equation is

an iterative process. Start the process assuming no relationship between y

and SOI (that is, setting

(0)

= 0) and setting

(0)

=0.5147 (the mle of μ

computed in Example 4.6). r code for implementing the algorithm explicitly

using the Fisher scoring algorithm is shown in Sect. 4.14 (p. 204). The output

is shown below. The iterations converge rapidly:

> # Details of the iterations, using an R function FitModelMle()

> # that was specifically written for this example (see Sect 4.14)

> m1.quilpie <- FitModelMle(y=quilpie$y, x=quilpie$SOI)

> m1.quilpie$coef.vec # Show the estimates at each iteration

[,1] [,2]

[1,] 0.51470588 0.0000000

[2,] 0.04382413 0.1146656

[3,] 0.05056185 0.1422438

[4,] 0.04820676 0.1463373

[5,] 0.04812761 0.1464183

[6,] 0.04812757 0.1464184

[7,] 0.04812757 0.1464184

[8,] 0.04812757 0.1464184

The output indicates that the algorithm has converged quickly, and that the

ﬁtted model has the systematic component

log

ˆμ

1 − ˆμ

=0.04813 + 0.1464x, (4.17)

where x is the monthly average soi. Figure 4.6 displays the model plotted

with the data. The linear regression model with the linear systematic compo-

nent (4.10) is also shown. The linear regression model is inappropriate: neg-

ative probabilities of exceeding the rainfall threshold are predicted for large

−20 −10 0 10 20

0.0

0.2

0.4

0.6

0.8

1.0

July average SOI

Prob. of rainfall exceeding threshold

Linear regression model

Adopted model

Fig. 4.6 The ﬁtted linear regression model (4.10) and the adopted model (4.17). The

points have a small amount of added randomness in the vertical direction to avoid

overplotting (Example 4.10)

188 4 Beyond Linear Regression: The Method of Maximum Likelihood

−48

−46

−44

−42

−40

−39

−38.5

−38

−0.4 −0.2 0.0 0.2 0.4

0.00

0.05

0.10

0.15

0.20

0.25

0.5147

Fig. 4.7 A contour plot showing the log-likelihood function for the Quilpie rainfall data

(note the contours are not equally spaced). The solid point in the centre is the maximum

likelihood estimate. The gray lines and gray points show the path of the estimates on

the likelihood surface; the larger gray point in the bottom right corner is the starting

point (Example 4.15)

negative values of the soi, and probabilities exceeding one are predicted for

large positive values of the soi. Figure 4.7 shows the log-likelihood surface

for the example, and the progress of the iterations. 

The ﬁtted model explains the relationship between the soi and the proba-

bility of exceeding 10 mm of total July rainfall at Quilpie. Rearranging (4.17),

ˆμ =

1+exp(−0.04813 − 0.1464x)

Then, ˆμ → 0asx →−∞, and ˆμ → 1asx →∞. This shows that larger values

of the soi are associated with higher probabilities of exceeding 10 mm, and

lower values of the soi are associated with lower probabilities of exceeding

10 mm (as seen in Fig. 4.6). When the soi is zero, the probability of exceeding

10 mm is computed as approximately 51%.

Example 4.16. For the Bernoulli model ﬁtted to the Quilpie rainfall data, we

can continue Example 4.15. Since the values of μ

are unknown, the diagonal

elements of the inverse of the information matrix evaluated at

μ (at the ﬁnal

iteration) give the estimated variance of the parameter estimates:

4.9 Properties of MLEs 189

> inf.mat.inverse <- solve( m1.quilpie$inf.mat )

> # Note: 'solve' with one matrix input computes a matrix inverse

> inf.mat.inverse

Constant x

Constant 0.0775946484 -0.0006731683

x -0.0006731683 0.0018385219

Hence the standard errors are:

> std.errors <- sqrt( diag( inf.mat.inverse ) )

> std.errors

Constant x

0.27855816 0.04287799



The Fisher scoring iteration is used for parameter estimation with glms

used later in this book. However, writing corresponding r functions for each

diﬀerent model, as for the Quilpie rainfall example and shown in Sect. 4.14

(p. 204), is clearly time-consuming, error-prone and tedious. In Chap. 5,the

structure of glms is established that enables the Fisher scoring iteration

to be written in a general form applicable to all types of glms, and hence

a common algorithm is established for ﬁtting the models. Because of the

structure established in Chap. 5, a simple-to-use r function (called glm())is

used to ﬁt the generalized linear models in this book, avoiding the need to

develop problem-speciﬁc r code (as in the example above).

4.9 Properties of MLEs

4.9.1 Introduction

Maximum likelihood estimators have many appealing properties, which we

state in this section without proof. The properties in this section hold under

standard conditions that are true for models in this book. The main assump-

tion is that information about the unknown parameters increases with the

number of observations n.

4.9.2 Properties of MLEs for One Parameter

The mle of ζ, denoted

ζ, has the following appealing properties.

1. Mlesareinvariant. This means that if s(ζ) is a one-to-one function of

ζ, then s(

ζ)isthemle of s(ζ).

190 4 Beyond Linear Regression: The Method of Maximum Likelihood

2. Mlesareasymptotically unbiased. This means that E[

ζ]=ζ as n →∞.

For small samples, the bias may be substantial. In some situations (such

as the parameter estimates

in normal linear regression models), the

mle is unbiased for all n.

3. Mlesareasymptotically eﬃcient. This means that no other asymptoti-

cally unbiased estimator exists with a smaller variance. Furthermore, if an

eﬃcient estimator of ζ exists, then it must be asymptotically equivalent

ζ.

4. Mlesareconsistent. This means that the mle converges to the true value

of ζ for increasing n:

ζ → ζ as n →∞.

5. Mlesareasymptotically normally distributed. This means that if ζ

the true value of ζ,

ζ ∼ N (ζ

, 1/I(ζ

)) , (4.18)

as n →∞, where N denotes the normal distribution. Importantly, this

shows that the reciprocal of the information is the variance

ζ as n →∞:

var[

ζ]=1/I(ζ

). (4.19)

Consequently, the standard error of



I(ζ

* 4.9.3 Properties of MLEs for Many Parameters

The properties of mles described above can be extended to more than one

parameter, using vector notation. The mle of ζ, denoted

ζ, has the following

appealing properties, which are stated without proof but which hold under

standard conditions that are true for models in this book. The main assump-

tion is that information about

ζ (as measured by the eigenvalues of I(ζ))

increases with the number of observations n.

1. Mlesareinvariant. This means that if s(ζ) is a one-to-one function of

ζ, then s(

ζ)isthemle of s(ζ).

2. Mlesareasymptotically unbiased. This means that E[

ζ]=ζ as n →∞.

For small samples, the bias may be substantial. In some situations (such

as the parameter estimates

in normal linear regression models), the

mle is unbiased for all n.

3. Mlesareasymptotically eﬃcient. This means that no other asymptoti-

cally unbiased estimator exists with a smaller variance. Furthermore, if an

eﬃcient estimator of ζ exists, then it must be asymptotically equivalent

ζ.

4. Mlesareconsistent. This means that the mle converges to the true value

of ζ for increasing n:

ζ → ζ as n →∞.

4.10 Hypothesis Testing: Large Sample Asymptotic Results 191

5. Mlesareasymptotically normally distributed. This means that if ζ

the true value of ζ,

ζ ∼ N



, I(ζ

)

−1



, (4.20)

as n →∞, where N

denotes the multivariate normal distribution of

dimension q,andq is the length of ζ. Importantly, this shows that the

inverse of the information matrix is the covariance matrix of

ζ as n →∞:

var[

ζ]=I(ζ

)

−1

. (4.21)

Consequently, the standard error of

is the corresponding diagonal ele-

ment of I(ζ

)

−1/2

. Equation (4.20) may be written equivalently as

(

ζ − ζ

)

I(ζ

)(

ζ − ζ

) ∼ χ

(4.22)

as n →∞.

4.10 Hypothesis Testing: Large Sample Asymptotic

Results

4.10.1 Introduction

After ﬁtting a model, asking questions and testing hypotheses about the

model is natural. Start by considering models with only one parameter, and

hypotheses concerning this single parameter. Speciﬁcally, we test the null

hypothesis that H

: ζ = ζ

for some postulated value ζ

against the two-

tailed alternative H

: ζ = ζ

Three methods for testing the null hypothesis H

: ζ = ζ

are possible

(Fig. 4.8). A Wald test is based on the distance between

ζ and ζ

(Fig. 4.8,

left panel). After normalizing by an estimate of the variance of

ζ, write

W =

(

ζ − ζ

)

var[

ζ]

where var[

ζ]=1/I(

ζ)from(4.9). If H

is true, then W follows a χ

distribu-

tion as n →∞.IfW is small, the distance

ζ − ζ

is small, which means the

estimate

ζ is close to the hypothesized value ζ

and is evidence to support

When testing about one parameter, the square root of W is often used as

the test statistic, when we write Z =

√

W . Then, Z ∼ N(0, 1) as n →∞.

Using Z enables testing with one-sided alternative hypotheses.

The score test examines the slope of the log-likelihood near ζ

(Fig. 4.8,

centre panel). By deﬁnition, the slope of the log-likelihood is zero at

ζ,soifthe

192 4 Beyond Linear Regression: The Method of Maximum Likelihood

Wald test

Log−likelihood

Score test

Log−likelihood

Likelihood ratio test

Log−likelihood

l(ζ=ζ

)

l(ζ=ζ

)

ΔΔ

Fig. 4.8 Three ways of testing the hypothesis that ζ = ζ

. The Wald test measures the

change in the ζ dimension; the score test measures the slope of the likelihood function

at ζ

; the likelihood ratio test measures the change in the likelihood dimension. The

likelihood curve is actually computed using the Quilpie rainfall data (Sect. 4.10.1)

slope of the log-likelihood at ζ

is near zero, then ζ

is near

ζ. Normalizing by

the variance of the slope, using var[U(ζ

)] = I(ζ

) from Sect. 4.5.3 (p. 179),

write

S =

U(ζ

)

I(ζ

)

If H

is true, then S follows a χ

distribution as n →∞.IfS is small, then

the slope at ζ

is close to zero, and the estimate

ζ is close to the hypothesized

value ζ

which is evidence to support H

. Notice that computing S does not

require knowledge of

ζ; instead, S is evaluated at ζ

, so the estimate of ζ is

not needed. For this reason, score tests are often simpler than Wald tests.

When testing about one parameter, the square root of S is often used, where

√

S ∼ N (0, 1) as n →∞.Using

√

S enables testing with one-sided alternative

hypotheses.

The likelihood ratio test is based on the distance between the maximum

possible value of the log-likelihood (evaluated at

ζ) and the likelihood evalu-

ated at ζ

(Fig. 4.8, right panel):

L =2{(

ζ; y) − (ζ

; y)}.

Twice the diﬀerence between the log-likelihoods is used, because then L fol-

lows a χ

distribution as n →∞.IfL is small, then the diﬀerence between

the log-likelihoods is small, and the estimate

ζ is close to the hypothesized

value ζ

which is evidence to support H

Note that W , S and L all have approximate χ

distributions. To compute

P -values corresponding to each statistic, refer to a χ

distribution. As n →∞,

all three test statistics are equivalent.

4.10 Hypothesis Testing: Large Sample Asymptotic Results 193

Example 4.17. For the Quilpie rainfall data (data ﬁle: quilpie), and the

model based on estimating μ (and ignoring soi), consider testing H

: μ =0.5

using all three tests (that is, use μ

=0.5). For reference, recall that

U(μ)=



i=1

− nμ

μ(1 − μ)

n(ˆμ − μ)

μ(1 − μ)

and I(μ)=

μ(1 − μ)

from Examples 4.7 and 4.8. Also, ˆμ =0.5147 and n = 68. For the Wald test,

compute

W =

(ˆμ − μ

)

ˆμ(1 − ˆμ)/n

where W ∼ χ

as n →∞.Usingr:

> muhat <- mean( quilpie$y )

> mu0 <- 0.5

> n <- length(quilpie$y)

> varmu <- muhat*(1-muhat)/n

> W <- (muhat - mu0)^2 / varmu; W

[1] 0.05887446

The score statistic is

S =

U(μ

)

I(μ

)



nˆμ − nμ



nμ

(1 − μ

)

where S ∼ χ

as n →∞. Notice that

√

S =

ˆμ − μ



(1 − μ

)/n

where

√

S ∼ N(0, 1) as n →∞. This expression for

√

S is the usual test

statistic for a one-sample proportion problem. Using r:

> S <- (muhat - mu0)^2 / ( mu0*(1-mu0)/n ); S

[1] 0.05882353

For the likelihood ratio test statistic, compute the log-likelihood at μ

and

at ˆμ, then compute L =2

(ˆμ; y) − (μ

; y)

.Usingr:

> Lmu0 <- sum( dbinom(quilpie$y, 1, mu0, log=TRUE ) )

> Lmuhat <- sum( dbinom(quilpie$y, 1, muhat, log=TRUE ) )

> L <- 2*(Lmuhat - Lmu0); L

[1] 0.05883201

In this example, W , S and L have similar values:

> c( Wald=W, score=S, LLR=L)

Wald score LLR

0.05887446 0.05882353 0.05883201

194 4 Beyond Linear Regression: The Method of Maximum Likelihood

For each statistic, the asymptotic theory suggests referring to a χ

distribu-

tion. Assuming the likelihood-theory approximations are sound, the corre-

sponding two-tailed P -values are:

> P.W <- pchisq(W, df=1, lower.tail=FALSE) # Wald

> P.S <- pchisq(S, df=1, lower.tail=FALSE) # Score

> P.L <- pchisq(L, df=1, lower.tail=FALSE) # Likelihood ratio

> round(c(Wald=P.W, Score=P.S, LLR=P.L), 5)

Wald Score LLR

0.80828 0.80837 0.80835

(The function pchisq computes the cumulative distribution function for the

chi-square distribution with df degrees of freedom.) The two-tailed P -values

and conclusions are similar in all cases: the data are consistent with the null

hypothesis that μ =0.5. Recall that none of these P -values are exact; each

statistic follows a χ

distribution as n →∞. 

* 4.10.2 Global Tests

The three tests used in the last section were applied when only one parame-

ter appears in the model. These tests can also be used to test hypotheses for

all parameters ζ simultaneously in situations where more than one param-

eter appears. Consider testing the hypothesis H

: ζ = ζ

, where ζ

is the

postulated value of ζ. In this context, the three test statistics are:

Wald: W =(

ζ − ζ

)

ζ)(

ζ − ζ

);

Score: S = U(ζ

)

I(ζ

)

−1

U(ζ

);

Likelihood ratio: L =2{(

ζ; y) − (ζ

; y)}. (4.23)

Large values are evidence against H

. Each statistic follows a χ

distribution

as n →∞, where q is the length of ζ. This result can be used to ﬁnd the

corresponding two-tailed P -values.

Example 4.18. For the Quilpie rainfall data (data set: quiplie), consider

the model with log{μ/(1 − μ)} = β

+ β

x where x is the value of the soi

(Example 4.10,p.180). If μ =0.5 regardless of the soi, then log{μ/(1−μ)} =

0 for all values of the soi. This means that β

= β

= 0. Hence, consider

testing β =[0, 0]

, where

β is:

> m1.quilpie$coef

[1] 0.04812757 0.14641837

Note that β

=[0, 0]

, and so (

β − β

β. Also, the inverse of the infor-

mation matrix is given in Example 4.14 (p. 186). Using r:

4.10 Hypothesis Testing: Large Sample Asymptotic Results 195

> beta0 <- c(0, 0); betahat <- m1.quilpie$coef

> betahat.minus.beta0 <- betahat - beta0

> W.global <- t(betahat.minus.beta0) %*% m1.quilpie$inf.mat %*%

betahat.minus.beta0

> p.W.global <- pchisq( W.global, df=2, lower.tail=FALSE)

> round(c(W.stat=W.global, P=p.W.global), 6)

W.stat P

11.794457 0.002747

For the score test, all quantities must be computed under H

, so the informa-

tion matrix must be recomputed at μ =0.5 (the value of μ when β =[0, 0]

> U <- MakeScore(cbind(1, quilpie$SOI), quilpie$y, beta0)

> # Note: MakeScore() was written for this example (Sect. 4.14)

> inf.mat.score <- MakeExpInf( cbind(1, quilpie$SOI), 0.5)

> inf.mat.inverse <- solve( inf.mat.score )

> S.global <- t(U) %*% inf.mat.inverse %*% U

> p.S.global <- pchisq( S.global, df=2, lower.tail=FALSE)

> round(c(score.stat=S.global, P=p.S.global), 6)

score.stat P

15.924759 0.000348

For the likelihood ratio test, ﬁrst compute the two likelihoods:

> mu <- m1.quilpie$mu

> Lbeta0 <- sum( dbinom(quilpie$y, 1, 0.5, log=TRUE ) )

> Lbetahat <- sum( dbinom(quilpie$y, 1, mu, log=TRUE ) )

> L.global <- 2*(Lbetahat - Lbeta0)

> p.L.global <- pchisq( L.global, df=2, lower.tail=FALSE)

> round(c(LLR.stat=L.global, P=p.L.global), 6)

LLR.stat P

18.367412 0.000103

Recall each statistic follows a χ

distribution as n →∞. Nonetheless, the

three diﬀerent tests produce diﬀerent two-tailed P -values:

> test.info <- array(dim=c(3, 2)) # Array to hold the information

> rownames(test.info) <- c("Wald","Score","Likelihood ratio")

> colnames(test.info) <- c("Test statistic","P-value")

> test.info[1,] <- c(W.global, p.W.global)

> test.info[2,] <- c(S.global, p.S.global)

> test.info[3,] <- c(L.global, p.L.global)

> round(test.info, 6)

Test statistic P-value

Wald 11.79446 0.002747

Score 15.92476 0.000348

Likelihood ratio 18.36741 0.000103

The conclusions will almost certainly be the same here whichever test statistic

is used: the evidence is not consistent with H

: β =[0, 0]

.TheP -values from

the score and likelihood ratio tests are similar, but the Wald test P -value is

about ten times larger. 

196 4 Beyond Linear Regression: The Method of Maximum Likelihood

* 4.10.3 Tests About Subsets of Parameters

So far, the Wald, score and likelihood ratio testing procedures have consid-

ered tests about all the parameters in the model, either the single parameter

(Sect. 4.10.1) or all of the many parameters (Sect. 4.10.2). However, com-

monly tests are performed about subsets of the parameters.

To do this, partition ζ so that ζ

=[ζ

, ζ

], where ζ

has length q

and ζ

has length q

, and the null hypotheses H

: ζ

= ζ

is to be tested.

Partition the information matrix correspondingly as

ζ)=





so that I

is a q

× q

matrix, and I

is a q

× q

matrix. Then write

ζ)

−1





(Note that I

=(I

−I

−1

)

−1

.) Consider testing H

: ζ

= ζ

against

the two-tailed alternative, where ζ

is some postulated value. ζ

is a nuisance

parameter, and is free to vary without restriction. Now deﬁne ζ

∗

, ζ

In other words, ζ

∗

is the vector of the mle for ζ

under H

, and the value

of ζ

deﬁned in H

. Then the three test statistics are:

Wald: W =(

− ζ

)

−1

(

− ζ

);

Score: S = U(ζ

∗

)

I(ζ

∗

)

−1

U(ζ

∗

); (4.24)

Likelihood ratio: L =2

(

ζ; y) − (ζ

∗

; y)

. (4.25)

Each statistic follows a χ

distribution as n →∞. Large values are evidence

against H

Example 4.19. For the Quilpie rainfall data (data ﬁle: quiplie), possibly soi

is not signiﬁcantly related to the probability of the rainfall exceeding the

threshold, and is not necessary in the model. An appropriate hypothesis to

test is H

: β

= 0, so that β

plays the role of ζ

and β

plays the role

of ζ

We can test the hypothesis using the score test (the Wald and likelihood

ratio tests for this hypothesis will be demonstrated in Example 4.20). First,

evaluate the log-likelihood where β

=0:

4.10 Hypothesis Testing: Large Sample Asymptotic Results 197

> m2.quilpie <- FitModelMle(quilpie$y); m2.quilpie$coef

[1] 0.0588405

> zeta.star <- c(m2.quilpie$coef, 0) # Add the coefficient for beta1 = 0

> Xvars <- cbind( rep(1, length(quilpie$y)), # Constant

quilpie$SOI )

> U.vec <- MakeScore( Xvars, y=quilpie$y, zeta.star); U.vec

[,1]

[1,] -2.331468e-15

[2,] 1.477353e+02

Note that since ζ

∗

, 0]

, the ﬁrst element of U(ζ

∗

) is zero (to computer

precision) since the mle is computed for this ﬁrst parameter. Eﬀectively,

since U(ζ

∗

) has only one non-zero component, the matrix computation (4.24)

simpliﬁes considerably:

> inf.mat2 <- MakeExpInf( Xvars, m2.quilpie$mu )

> inf.mat.inv2 <- solve( inf.mat2 )

> scoretest <- t( U.vec ) %*% inf.mat.inv2 %*% U.vec

> drop(scoretest)

[1] 15.87967

Since the score statistic has an approximate chi-square distribution with one

degree of freedom, the two-tailed P -value is approximately

> p.score <- pchisq( scoretest, df=1, lower.tail=FALSE)

> drop(p.score)

[1] 6.749985e-05

The evidence is not consistent with β

=0. 

4.10.4 Tests About One Parameter in a Set of

Parameters

A common situation is to test the hypothesis H

: β

= β

when a group

of parameters are in the model. This is a special case of the situation in

Sect. 4.10.3 when q

= 1. While the Wald, score and likelihood ratio test

statistics can all be used in this situation, the Wald statistic conveniently

reduces to

W =

(

− ζ

)

var[

]

, (4.26)

which is distributed as χ

as n →∞. In this situation, working with Z =

√

is more common (and permits one-sided alternative hypotheses), giving

Z =

− ζ



var[

]

, (4.27)

where Z ∼ N(0, 1) as n →∞.

198 4 Beyond Linear Regression: The Method of Maximum Likelihood

The likelihood ratio test is conducted by evaluating the log-likelihood un-

der H

,say(β

; y) (that is, setting β

to β

) and evaluating the likelihood

under the alternative hypothesis, say (

; y) (that is, setting β

), and

computing L =2{(

; y) − (β

; y)}. L follows a χ

distribution as n →∞.

Example 4.20. For the Quilpie rainfall data (data ﬁle: quiplie), possibly soi

is not signiﬁcantly related to the probability of the rainfall exceeding the

threshold. An appropriate hypothesis to test is H

: β

= 0. A Wald test is

conducted using either

W =

(

− 0)



(1 − μ

or Z =

− 0





(1 − μ

using results from Examples 4.14 and 4.16.Inr:

> m1.quilpie <- FitModelMle(y=quilpie$y, x=quilpie$SOI) # Refit

> mu <- m1.quilpie$mu

> var.beta1 <- 1 / sum( mu * (1-mu) * quilpie$SOI^2 )

> se.beta1 <- sqrt(var.beta1); Z <- m1.quilpie$coef[2] / se.beta1; Z

[1] 3.420204

Since Z ∼ N(0, 1) as n →∞, the two-tailed P -value is approximately

> p.Z <- 2 * pnorm( Z, lower.tail=FALSE ) # Two-tailed P-value

> round( c(Z=Z, P=p.Z), 6)

3.420204 0.000626

Exactly the same two-tailed P -value results if W = Z

is used as the test

statistic, after referring to a χ

distribution:

> W <- Z^2; p.W <- ( pchisq( W, df=1, lower.tail=FALSE ) )

> round( c(W=W, P=p.W), 6)

11.697796 0.000626

Consider testing the same hypothesis using the likelihood ratio test statistic.

For the ﬁtted model, the log-likelihood is

> llh.full <- sum( dbinom( quilpie$y, size=1, prob=m1.quilpie$mu) )

> llh.full

[1] 42.16348

Under H

, when β

= 0, the model must be ﬁtted again:

> ### Fit reduced model:

> m2.quilpie <- FitModelMle(quilpie$y); m2.quilpie$coef

[1] 0.0588405

4.10 Hypothesis Testing: Large Sample Asymptotic Results 199

Then the log-likelihood for this reduced model is

> llh.reduced <- sum( dbinom( quilpie$y, size=1, prob=m2.quilpie$mu) )

> llh.reduced

[1] 34.02941

The values of L and the corresponding two-tailed P -value are

> L <- 2*( llh.full - llh.reduced )

> p.lrt <- pchisq( L, df=1, lower.tail=FALSE)

> round( c(L=L, P=p.lrt), 6)

16.268137 0.000055

The three test statistics and corresponding P -values are very similar, but

diﬀerent (the score test was performed in Example 4.19):

> test.info <- array(dim=c(3, 2))

> rownames(test.info) <- c("Wald","Score","Likelihood ratio")

> colnames(test.info) <- c("Test statistic","P-value")

> test.info[1,] <- c(W, p.W); test.info[2,] <- c(scoretest, p.score)

> test.info[3,] <- c(L, p.lrt); round(test.info, 6)

Test statistic P-value

Wald 11.69780 0.000626

Score 15.87967 0.000067

Likelihood ratio 16.26814 0.000055

The data are inconsistent with the null hypothesis, and suggest soi is nec-

essary in the model. Again, the P-values from the score and likelihood ratio

tests are similar, but the Wald test P -value is about ten times larger. 

4.10.5 Comparing the Three Methods

Three methods have been discussed for testing H

: β

= 0 for the Quilpie

rainfall data (Example 4.20): the Wald, score and likelihood ratio tests. While

the conclusions drawn from these tests are probably the same here, the P -

values are diﬀerent for the three tests. The P -value from the Wald test is

larger than the others by a factor of 10 approximately. Referring the statistics

to a χ

distribution in each case only gives approximate P-values, as the χ

assumption applies asymptotically as n →∞. In practice, the asymptotic

results apply when n is much larger than the number of parameters, so that

all unknown parameters become well estimated. (In some cases, such as when

y follows a normal distribution, the χ

approximations are exact even for

small sample sizes.)

Of the three tests, the Wald test is usually the easiest to perform, be-

cause the necessary information (the parameter estimates and the standard

errors of the parameters) are computed as a direct result of ﬁtting the model

using the algorithm in Sect. 4.8. This means that a simple explicit formula

200 4 Beyond Linear Regression: The Method of Maximum Likelihood

exists for testing hypotheses about a single parameter (4.26). However, W

has undesirable statistical properties, particularly with binomial distributions

(Sect. 9.9). Under some circumstances, as

−ζ

increases the test statistic W

approaches zero, in contrast to the expectations of Fig. 4.8. This is sometimes

called the Hauck–Donner eﬀect [8]. The results from the score and likelihood

ratio tests are more reliable.

Score tests often require less computational eﬀort. For example, score tests

concerning β

do not require the estimate

. Likelihood ratio tests require

two models to be ﬁtted: the model under the null hypothesis and the model

under the alternative hypothesis.

4.11 Conﬁdence Intervals

* 4.11.1 Conﬁdence Regions for More Than One

Parameter

For the Wald, score and likelihood ratio statistics, conﬁdence intervals can

be formed for parameters. A joint 100(1 − α)% conﬁdence region for all the

unknown parameters ζ simultaneously can be obtained from the Wald, score

or likelihood ratio statistics, as the two vector solutions to

Wald: (

ζ − ζ)

ζ)(

ζ − ζ) ≤ χ

q,1−α

(4.28)

Score: U(ζ)

I(ζ)

−1

U(ζ) ≤ χ

q,1−α

(4.29)

Likelihood ratio: 2

(

ζ; y) − (ζ; y)

≤ χ

q,1−α

(4.30)

where ζ is the true value, and q is the length of ζ. General solutions to these

equations are diﬃcult to ﬁnd. The intervals are only approximate in general,

as they are based on the distributional assumptions which apply as n →∞.

4.11.2 Conﬁdence Intervals for Single Parameters

A conﬁdence interval for a single parameter ζ

(Fig. 4.9) has the limits of

the conﬁdence interval as the two values of ζ

satisfying the appropriate

condition (4.28)–(4.30). Wald conﬁdence intervals are based on the values of

ζ at a given distance either side of

ζ. Score conﬁdence intervals are based on

the values of ζ at which the slope of the likelihood function meets appropriate

criteria. Likelihood-ratio conﬁdence intervals are based on the values of ζ

such that diﬀerence between the maximum value of the likelihood and the

likelihood function meet appropriate criteria.

4.11 Conﬁdence Intervals 201

Wald interval

Lower

limit

Upper

limit

Log−likelihood

Score interval

Lower

limit

Upper

limit

Log−likelihood

LR interval

Lower

limit

Upper

limit

Log−likelihood

Fig. 4.9 Three ways of computing conﬁdence intervals for a one-dimensional situation.

The Wald conﬁdence interval is symmetric by deﬁnition; the score and the likelihood

ratio conﬁdence intervals are not necessarily symmetric (Sect. 4.11)

For a single parameter, the approximate 100(1 −α)% conﬁdence interval

based on the Wald statistic is obtained directly from (4.27):

− z

∗



var[

] <ζ

+ z

∗



var[

]

where z

∗

is the quantile of the standard normal distribution such that an area

α/2 is in each tail. Wald conﬁdence intervals are most commonly used, be-

cause this explicit solution is available, and because

and



var[

] are found

directly from the ﬁtting algorithm (Sect. 4.8). Note the conﬁdence interval is

necessarily symmetric for the Wald statistic.

Conﬁdence intervals for single parameters based on the score and likeli-

hood statistics are harder to ﬁnd, as they require numerically solving the

corresponding equations that come from the relevant statistics. The limits of

the conﬁdence interval are the two solutions to

Score: U(ζ)

/I(ζ) ≤ χ

1,1−α

(4.31)

Likelihood ratio: 2

(

ζ; y) − (ζ; y)

≤ χ

1,1−α

(4.32)

Example 4.21. Consider the model ﬁtted to the Quilpie rainfall data (data

ﬁle: quiplie)usingsoi as an explanatory variable (Example 4.6,p.174),

and ﬁnding a conﬁdence interval for β

. The log-likelihood evaluated at the

mlesofβ

and β

is (

; y)=−37.95 and χ

1,1−α

=3.841 for a 95%

conﬁdence interval. Then, from (4.30), the limits of the conﬁdence interval

are the two solutions to

−37.95 − (

,β

; y)

=3.841, (4.33)

202 4 Beyond Linear Regression: The Method of Maximum Likelihood

Tabl e 4. 6 Conﬁdence intervals for β

, using the Wald, score and likelihood ratio statis-

tics. Note that

=0.1464 (Sect. 4.11)

Type of interval Lower Upper

Wald: 0.06238 0.2305

Score: 0.06552 0.2289

Likelihood-ratio: 0.07191 0.2425

a non-linear equation which must be solved numerically. One solution will be

less than

=0.1464, and one solution greater than

=0.1464.

In Fig. 4.9, conﬁdence intervals are shown based on the Wald, score and

likelihood-ratio statistics. The Wald conﬁdence interval is symmetric, by def-

inition. The conﬁdence intervals based on the score and log-likelihood func-

tions are not necessarily symmetric (Table 4.6), since the log-likelihood func-

tion is not exactly symmetric about

. 

4.12 Comparing Non-nested Models: The AIC and BIC

In Sect. 2.11,theaic and bic were used to compare non-nested linear regres-

sion models. More generally, the aic and bic can be used to compare any

non-nested models based on a speciﬁc probability distribution, by using the

log-likelihood and penalizing the complexity of models. Formally, the aic is

deﬁned [1] in terms of the log-likelihood as

aic = −2(

,...,

; y)+

2 × (Number of unknown parameters), (4.34)

where (

,...,

; y) is the log-likelihood evaluated at the mles for the model

under consideration. The aic penalizes the log-likelihood by the number of

unknown parameters using k = 2. Using this deﬁnition, smaller values of the

aic (closer to −∞) represent better models.

Similarly, the bic is deﬁned as

bic = −2(

,...,

; y)+

(log n) × (Number of unknown parameters). (4.35)

The bic penalizes the log-likelihood by the number of unknown parameters

using k = 2 log n. The results in Sect 2.11 (p. 70) are simply those for (4.34)

and (4.35) applied to normal linear regression models (Problem 4.10), ignor-

ing all constants.

4.12 Comparing Non-nested Models: The AIC and BIC 203

Example 4.22. Consider the model quilpie.m1 ﬁtted to the Quilpie rainfall

data quiplie in Example 4.15 (p. 187). The aic and bic are:

> LLH <- m1.quilpie$LLH

> m1.aic <- -2 * LLH+2*length(m1.quilpie$coef)

> m1.bic <- -2 * LLH + log(length(quilpie$y)) * length(m1.quilpie$coef)

> c(AIC=m1.aic, BIC=m1.bic)

AIC BIC

79.90060 84.33962

Rather than using the soi as an explanatory variable, an alternative is to

use the soi phases [14]. The soi can be classiﬁed into one of ﬁve phases,

depending on the soi in the current and previous months (see ?quilpie for

more details). For ﬁve soi phases, four dummy variables are needed, so the

total number of estimated parameters is ﬁve (including the constant). The

ﬁtted model is:

> quilpie$Phase <- factor( quilpie$Phase )

> Xvars <- with( quilpie, model.matrix( ~ Phase))#Create dummy vars

> head(Xvars)

(Intercept) Phase2 Phase3 Phase4 Phase5

1 11000

2 10001

3 10100

4 11000

5 10100

6 10010

> phase.quilpie <- FitModelMle(quilpie$y, x=Xvars, add.constant=FALSE )

(Notice the use of model.matrix() to automatically deﬁne the dummy vari-

ables for soi phases.) The two models m1.quilpie and phase.quilpie are

not nested, so comparing the models using the likelihood ratio test is inap-

propriate. Instead, the aic and bic are:

> LLH <- phase.quilpie$LLH

> m2.aic <- -2 * LLH+2*length(phase.quilpie$coef)

> m2.bic <- -2 * LLH + log(length(quilpie$y)) * length(phase.quilpie$coef)

> c( "AIC (SOI model)"=m1.aic, "AIC (SOI Phase model)"=m2.aic)

AIC (SOI model) AIC (SOI Phase model)

79.90060 75.79902

> c( "BIC (SOI model)"=m1.bic, "BIC (SOI Phase model)"=m2.bic)

BIC (SOI model) BIC (SOI Phase model)

84.33962 86.89656

The aic suggests that the model using the soi phases makes better predic-

tions than using the soi,astheaic for the soi model is closer to −∞.In

contrast, the bic suggests that the model using the soi is a superior model.



204 4 Beyond Linear Regression: The Method of Maximum Likelihood

4.13 Summary

Chapter 4 discusses situations where linear regression models do not apply,

and explores the theory of likelihood methods for estimation in these contexts.

We considered three important cases for which linear regression models

fail (Sect. 4.2):

• The response y is a proportion of a total number of counts, where 0 ≤

y ≤ 1.

• The response y is a count, where y =0, 1, 2,....

• The response y is positive continuous, where y>0.

A more general approach to regression models assumes the responses belong

to a family of distributions (Sect. 4.3).

For these models, maximum likelihood methods (Sect. 4.4) can be used for

estimation and hypothesis testing. We consider the one parameter (Sect. 4.5)

and two-parameter (Sect. 4.6) cases separately, and then the case of many

parameters using matrix algebra (Sect. 4.7).

Estimation using maximum likelihood includes a discussion of the score

equations (Sect. 4.5.1) the observed and expected information (Sect. 4.5.2)

and standard errors (Sect. 4.5.3). Then, the Fisher scoring algorithm for ﬁnd-

ing the maximum likelihood estimates was detailed (Sect. 4.8). Maximum

likelihood estimators are invariant, asymptotically unbiased, asymptotically

eﬃcient, consistent, and asymptotically normally distributed (Sect. 4.9).

Three types of inference are suggested by maximum likelihood methods:

Wald, score and likelihood ratio (Sect. 4.10 for hypothesis testing;. Sect. 4.11

for conﬁdence intervals). Asymptotic results are available for describing the

distribution of the Wald, score and likelihood ratio statistics, which apply as

n →∞(Sect. 4.10). Non-nested models can be compared using the aic or

the bic (Sect. 4.12).

* 4.14 Appendix: R Code to Fit Models to the Quilpie

Rainfall Data

In Example 4.15 (p. 187), a model was ﬁtted to the Quilpie rainfall data using

the ideas in Sect. 4.8 (p. 186). The r code used to ﬁt these models is shown

below. The purpose of the code is to demonstrate the application of the ideas

and formulae, and is not optimal r programming (for example, there is no

error checking). Later (Chap. 6), built-in r functions are described to ﬁt these

models without the need to use these functions. Notes on writing r functions

are given in Sect. A.3.11.

# Function for computing the information matrix:

MakeExpInf <- function(x, mu){

# Args:

4.14 Appendix: R Code to Fit Models to the Quilpie Rainfall Data 205

# x: The matrix of explanatory variables

# mu: The fitted values

# Returns:

# The expected information matrix

if ( length(mu) ==1)mu<-rep( mu, dim(x)[1])

mu <- as.vector(mu)

return( t(x) %*% diag( mu * (1 - mu) ) %*% x )

}

# Function for computing mu:

MakeMu <- function(x, beta){

# Args:

# x: The matrix of explanatory variables

# beta: The linear model parameter estimates

# Returns:

# The value of mu

eta <- x %*% beta

return(1/(1+exp( -eta)))

}

# Function for computing the score vector:

MakeScore <- function(x, y, beta){

# Args:

# x: The matrix of explanatory variables

# y: The response variable

# beta: The linear model parameter estimates

# Returns:

# The score matrix

mu <- MakeMu(x, beta)

return( t(x) %*% (y - mu) )

}

FitModelMle <- function(y, x=NULL, maxits=8, add.constant=TRUE){

# Args:

# y: The response variable

# x: The matrix of explanatory variables

# maxits: The maximum number of iteration for the algorithm

# add.constant: If TRUE, a constant is added to the x matrix

# (All models must have a constant term.)

# Returns:

# Information about the fitted glm

if ( is.null(x)){ # If no x given, ensure constant appears

allx <- cbind( Constant=rep( 1, length(y) ) )

} else {

allx <- x

if( add.constant ){

allx <- cbind( Constant=rep(1, length(y)), x)

}

num.x.vars <- dim(allx)[2] - 1 # Take one, because of constant

# Find initials: beta_0 = mean(y), and the other beta_j are zero

beta <- c( mean(y), rep( 0, num.x.vars ) )

206 4 Beyond Linear Regression: The Method of Maximum Likelihood

# Set up

beta.vec <- array( dim=c(maxits, length(beta) ) )

beta.vec[1,] <- beta

mu <- MakeMu( allx, beta )

score.vec <- MakeScore(allx, y, beta)

inf.mat <- MakeExpInf( allx, mu )

# Now iterate to update

for (i in (2:maxits)){

beta <- beta + solve( inf.mat ) %*% score.vec

beta.vec[i,] <- beta

mu <- MakeMu( allx, beta )

score.vec <- MakeScore(allx, y, beta)

inf.mat <- MakeExpInf( allx, mu )

}

# Compute log-likelihood

LLH <- sum( y*log(mu) + (1-y)*log(1-mu) )

return( list(coef = beta.vec[maxits,], # MLE of parameter estimates

coef.vec = beta.vec, # Estimates at each iteration

LLH = LLH, # The maximum log-likelihood

inf.mat = inf.mat, # The information matrix

score.vec = score.vec, # The score vector

mu = mu) ) # The fitted values

}

Problems

Selected solutions begin on p. 534. Problems preceded by an asterisk * refer

to the optional sections in the text, and may require matrix manipulations.

4.1. Show that an approximation to the Wald statistic can be developed from

the second-order Taylor expansion of the log-likelihood as follows. For this

problem, focus on just one of the regression parameters, say β

1. Write the ﬁrst three terms of the Taylor series expansion of (β

; y)ex-

panded about

2. Rearrange to show that the Wald statistic is approximately equal to

2{(β

; y) −(

; y)}, and hence show that the Wald statistic is approxi-

mately equivalent to a likelihood ratio test when β

−

is small.

*4.2.In Example 4.10 (p. 180), the information matrix was given for the

Bernoulli model ﬁtted to the Quilpie rainfall data. Prove the result in (4.15).

*4.3.In Sect. 4.7.3 (p. 184), two statements were made concerning the log-

likelihood, which we now prove. In this question, assume y is continuous.

4.14 Appendix: r Code to Fit Models to the Quilpie Rainfall Data 207

1. Working with just one observation, use the deﬁnition of the expected

value to show that

E[U(ζ)] =

∞

−∞

∂P(y; ζ)

∂ζ

dy. (4.36)

Then use (4.36)toshowthatE[U(ζ)] = 0.

2. Using that E[U (ζ)] = 0 and the deﬁnition of the variance, show that

var[U(ζ)] = E[U (ζ)U(ζ)

], which is I(ζ) (assuming the order of the

integration and diﬀerentiation can be reversed).

4.4. The normal distribution N(μ, σ

) has the probability function

P(y; μ, σ

√

2πσ

exp



−

(y −μ)

2σ



for σ>0, −∞ <μ<∞ and −∞ <y<∞. Consider estimating the mean μ

for the normal distribution when σ

is known, based on a sample y

,...,y

1. Determine the likelihood function and the log-likelihood function.

2. Find the score function.

3. Using the score function, ﬁnd the mle of μ.

4. Find the observed and expected information for μ.

5. Find the standard error for ˆμ.

6. Find the Wald test statistic W for testing H

: μ =0.

7. Find the score test statistic S for testing H

: μ =0.

8. Find the likelihood ratio test statistic L for testing H

: μ =0.

9. Show that W = S = L in this example.

4.5. The exponential distribution has the probability function

P(y; μ) = exp(−y/μ)/μ, (4.37)

for μ>0andy>0. Consider estimating the mean μ for the exponential

distribution based on a sample y

,...,y

1. Determine the likelihood function and the log-likelihood function.

2. Find the score function.

3. Using the score function, ﬁnd the mle of μ.

4. Find the observed and expected information for μ.

5. Show that the standard error for ˆμ is se(ˆμ)=ˆμ/

√

6. Show that the Wald test statistic for testing H

: μ =1isW =(ˆμ −

/(ˆμ

/n).

7. Show that the score test statistic for testing H

: μ =1isS = n(ˆμ − 1)

8. Show that the likelihood ratio test statistic for testing H

: μ =1is

L =2n(ˆμ − log ˆμ − 1).

9. Plot W , S and L for values of μ between 0.5 and 2, for n = 10. Comment.

10. Plot W, S and L for values of μ between 0.5 and 2, for n = 100. Comment.

208 4 Beyond Linear Regression: The Method of Maximum Likelihood

4.6. Use the r function rexp() to generate n = 100 random numbers from

the exponential distribution (4.37) with μ =1.(Inr, the parameter of the

exponential distribution is the rate where the rate is 1/μ.)

1. Use r to plot the likelihood function for the randomly generated data

from μ =0.75 to μ =1.25. Use vertical lines to show the location of ˆμ

and μ

=1.

2. Test the hypothesis H

: μ = 1 using the Wald, score and likelihood ratio

statistics developed in Problem 4.5.

3. Plot the Wald, score and likelihood ratio test statistics against possible

values of μ. Use a horizontal line to show the location of the critical value

of χ

. Compare the values of the test statistics for various values of ˆμ.

4. Find the standard error of ˆμ.

5. Find a 95% conﬁdence interval for μ using the Wald statistic.

*4.7.Consider a model based on the exponential distribution (4.37), where

log μ = β

+ β

x. Consider estimating the regression parameters based on a

sample y

,...,y

1. Show that the score vector has elements

∂

∂β



i=1

− μ

and

∂

∂β



i=1

− μ

2. Show that the second derivatives of the log-likelihood are

∂



∂β

= −



i=1

;

∂



∂β

= −



i=1

;

∂



∂β

= −



i=1

3. Using the results above, determine an expression for se(

4. Deﬁne the Wald test statistic for testing H

: β

=0.

4.8. The Poisson distribution has the probability function

P(y; μ)=

exp(−μ)μ

for μ>∞ and where y is a non-negative integer. Initially, consider estimating

the mean μ for the Poisson distribution, based on a sample y

,...,y

1. Determine the likelihood function and the log-likelihood function.

2. Find the score function U (μ).

3. Using the score function, ﬁnd the mle of μ.

4. Find the observed and expected information for μ.

5. Find the standard error for ˆμ.

*4.9.Following Problem 4.8, now consider the case where log μ = β

+ β

1. Find the score functions U (β

)andU(β

REFERENCES 209

2. Find the observed and expected information matrices.

3. Hence ﬁnd the standard errors of β

and β

4.10. Using the deﬁnition of the aic in (4.34), show that the formulae for

computing the aic in normal linear regression models is given by aic =

n log(rss/n)+2p



, as shown in (2.35)(p.71), after ignoring all constants.

References

[1] Akaike, H.: A new look at the statistical model identiﬁcation. IEEE

Transactions on Automatic Control 19(6), 716–723 (1974)

[2] Box, G.E.P.: Science and statistics. Journal of the American Statistical

Association 71, 791–799 (1976)

[3] Chatterjee, S., Handcock, M.S., Simonoﬀ, J.S.: A Casebook for a First

Course in Statistics and Data Analysis. John Wiley and Sons, New York

(1995)

[4] Dala, S.R., Fowlkes, E.B., Hoadley, B.: Risk analysis of the space shuttle:

pre-Challenger prediction of failure. Journal of the American Statistical

Association 84(408), 945–957 (1989)

[5] Dunn, P.K., Smyth, G.K.: Randomized quantile residuals. Journal of

Computational and Graphical Statistics 5(3), 236–244 (1996)

[6] Feigl, P., Zelen, M.: Estimation of exponential survival probabilities with

concomitant information. Biometrics 21, 826–838 (1965)

[7] Glaister, D.H., Miller, N.L.: Cerebral tissue oxygen status and psychomo-

tor performance during lower body negative pressure (LBNP). Aviation,

Space and Environmental Medicine 61(2), 99–105 (1990)

[8] Hauck Jr., W.W., Donner, A.: Wald’s test as applied to hypotheses in

logit analysis. Journal of the American Statistical Association 72, 851–

853 (1977)

[9] Maron, M.: Threshold eﬀect of eucalypt density on an aggressive avian

competitor. Biological Conservation 136, 100–107 (2007)

[10] McBride, J.L., Nicholls, N.: Seasonal relationships between Australian

rainfall and the southern oscillation. Monthly Weather Review 111(10),

1998–2004 (1983)

[11] Montgomery, D.C., Peck, E.A.: Introduction to Regression Analysis. Wi-

ley, New York (1992)

[12] Pook, M., Lisson, S., Risbey, J., Ummenhofer, C.C., McIntosh, P.,

Rebbeck, M.: The autumn break for cropping in southeast Australia:

trends, synoptic inﬂuences and impacts on wheat yield. International

Journal of Climatology 29, 2012–2026 (2009)

[13] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

[14] Stone, R.C., Auliciems, A.: soi phase relationships with rainfall in east-

ern Australia. International Journal of Climatology 12, 625–636 (1992)

Chapter 5

Generalized Linear Models:

Structure

Models are useful distillations of reality. Although wrong

by deﬁnition, they are the wind that blows away the fog

and cuts through the untamed masses of data to let us see

answers to our questions.

Kel ler [4, p. 97]

5.1 Introduction and Overview

Chapters 2 and 3 considered linear regression models. These models assume

constant variance, which demonstrably is not true for all data, as shown

in Chap. 4. Generalized linear models (glms) assume the responses come

from a distribution that belongs to a more general family of distributions,

and also permit more general systematic components. We ﬁrst review the

two components of a glm (Sect. 5.2) then discuss in greater detail the fam-

ily of distributions upon which the random component is based (Sect. 5.3),

including writing the probability functions in the useful dispersion model

form (Sect. 5.4). The systematic component of the glm is then considered in

greater detail (Sect. 5.5). Having discussed the two components of the glm,

glms are then formally deﬁned (Sect. 5.6), and the important concept of the

deviance function is introduced (Sect. 5.7). Finally, using a glm is compared

to using a regression model after transforming the response (Sect. 5.8).

5.2 The Two Components of Generalized Linear Models

Generalized linear models (glms) are regression models (Sect. 1.6), and so

consist of a random component and a systematic component. The random

and systematic components take speciﬁc forms for glms, which depend on

the answers to the following questions:

1. What probability distribution is appropriate? The answer determines the

random component of the model. The choice of probability distribution

may be suggested by the response data (for example, proportions of a

total suggest a binomial distribution), or knowledge of how the variance

changes with the mean.

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_5

211

212 5 Generalized Linear Models: Structure

2. How are the explanatory variables related to the mean of the response

μ? The answer suggests the systematic component of the model. Glms

assume a function linking the linear predictor η = β



j=1

the mean μ, such as log μ = η for example. That is, glms are regression

models linear in the parameters.

5.3 The Random Component: Exponential Dispersion

Models

5.3.1 Examples of EDMs

Glms assume the responses come from a distribution that belongs to a fam-

ily of distributions called the exponential dispersion model family (or edm

family, or just edms). Continuous edms include the normal and gamma dis-

tributions. Discrete edms include the Poisson, binomial and negative bino-

mial distributions. The edm family of distributions enables glms to be ﬁtted

to a wide range of data types, including binary data (Chap. 4), proportions

(Chap. 9), counts (Chap. 10), positive continuous data (Chap. 11), and posi-

tive continuous data with exact zeros (Chap. 12).

5.3.2 Deﬁnition of EDMs

Distributions in the edm family have a probability function (a probability

density function if y is continuous; a probability mass function if y is discrete)

of the form

P(y; θ, φ)=a(y,φ)exp



yθ − κ(θ)



(5.1)

where

• θ is called the canonical parameter.

• κ(θ) is a known function, and is called the cumulant function.

• φ>0isthedispersion parameter.

• a(y,φ) is a normalizing function ensuring that (5.1) is a probability

function. That is, a(y, φ) is the function of φ and y ensuring that

P(y; θ, φ) dy = 1 over the appropriate range if y is continuous, or the

function ensuring that



P(y; θ, φ) dy =1ify is discrete. The function

a(y, φ) cannot always be written in closed form.

The mean μ is a known function of the canonical parameter θ (Sect. 5.3.5).

The notation y ∼ edm(μ, φ) indicates that the responses come from a dis-

tribution in the edm family (5.1), with mean μ and dispersion parameter

φ. Deﬁnition (5.1) writes the form of an edm in canonical form. Other pa-

rameterizations are also possible, and the dispersion model form (Sect. 5.4)

is particularly important.

5.3 The Random Component: Exponential Dispersion Models 213

The support of y (the set of possible values for y) is denoted by S, where

S does not depend on the parameters θ and φ. The domain of θ, denoted

Θ, is an open interval of values satisfying κ(θ) < ∞ that includes zero. The

corresponding domain of μ is denoted Ω.

Example 5.1. The probability density function for the normal distribution

with mean μ and variance σ

P(y; μ, σ

√

2πσ

exp



−

(y −μ)

2σ



(5.2)

√

2πσ

exp



yμ −(μ

/2)

−

2σ



Comparing to (5.1), θ = μ is the canonical parameter, κ(θ)=μ

/2=θ

is the cumulant function, φ = σ

is the dispersion parameter, and a(y, φ)=

(2πσ

)

−1/2

exp{−y

/(2σ

)} is the normalizing function. The normal distri-

bution is an edm. 

Example 5.2. The Poisson probability function is usually written

P(y; μ)=

exp(−μ)μ

for μ>0andy =0,1,2,....Intheformof(5.1),

P(y; μ) = exp{y log μ − μ − log(y!)},

showing that θ = log μ is the canonical parameter, κ(θ)=μ,andφ =1.

The normalizing function is a(y, φ)=1/y!. The Poisson distribution is an

edm. 

Example 5.3. The binomial probability function is

P(y; μ, m)=





(1 − μ)

m(1−y)





exp





y log

1 − μ

+ log(1 − μ)



, (5.3)

where y =0, 1/m, 2/m,...1, and 0 <μ<1. Comparing to (5.1), θ =

log{μ/(1 −μ)} is the canonical parameter, κ(θ)=−log(1 −μ), φ =1/m and

a(y, φ)=





. The binomial distribution is an edm when m is known. 

Example 5.4. The Weibull distribution has the probability function

P(y; α, γ)=





α−1

exp



−







214 5 Generalized Linear Models: Structure

for y>0 with α>0andγ>0. Rewriting,

P(y; α, γ) = exp



−





+ log





+(α − 1) log



Inside the exponential function, a term of the form yθ cannot be extracted

unless α = 1. Hence, the Weibull distribution is not an edm in general. When

α = 1, the probability function is

P(y; γ) = exp(−y/γ)/γ =exp{−(y/γ) − log γ},

which is the exponential distribution (4.37) with mean γ. The exponential

distribution written in this form is an edm where θ = −1/γ is the canonical

parameter, κ(θ) = log γ and φ =1. 

5.3.3 Generating Functions

edms have many important and useful properties. One useful property is that

the moment generating function (mgf) always has a simple form, even if the

probability function cannot be written in closed form. The mean and variance

may be found from this simple mgf.

The moment generating function, denoted M (t), for some variable y with

probability function P(y)is

M(t)=E[e

⎧

⎪

⎨

⎪

⎩

P(y)e

dy for y continuous



y∈S

P(y)e

for y discrete,

for all values of t for which the expectation exists. The cumulant generating

function (or cgf) is then deﬁned as

K(t) = log M(t) = log E[e

for all values of t for which the expectation exists. The cgf is used to derive

the cumulants of a distribution, such as the mean (ﬁrst cumulant, κ

)and

the variance (second cumulant, κ

). The rth cumulant, κ

,is

K(t)

(

t=0

(5.4)

5.3 The Random Component: Exponential Dispersion Models 215

where the notation means to evaluate the indicated derivative at t =0.Using

the cgf, the mean and variance are (Problem 5.4):

E[y]=κ

dK(t)

(

t=0

and var[y]=κ

K(t)

(

t=0

. (5.5)

5.3.4 The Moment Generating and Cumulant

Functions for EDMs

The mgf, and hence cgf, for an edm has a very simple form. The mgf is

developed here for a continuous response, but the results also hold for discrete

distributions (Problem 5.6).

Using (5.1), the mgf for an edm is

M(t) = E[exp(ty)]

exp(ty)a(y,φ)exp



yθ − κ(θ)



=exp



κ(θ



) − κ(θ)



a(y, φ)exp



yθ



− κ(θ



)



dy,

where θ



= θ + tφ. The integral on the right is one, since the integrand is an

edm density function (5.1) written in terms of θ



rather than θ. This means

that the mgf and cumulant generating function (cgf) for an edm are

M(t) = exp



κ(θ + tφ) − κ(θ)



; (5.6)

K(t)=

κ(θ + tφ) − κ(θ)

. (5.7)

Using (5.7), the rth cumulant for an edm is (Problem 5.5)

= φ

r−1

κ(θ)

dθ

. (5.8)

For this reason, κ(θ) is called the cumulant function.

Example 5.5. For the normal distribution, the results in Example 5.1 can be

used with (5.7) to obtain

K(t)=

(μ + tσ

)

2σ

−

2σ

= μt +



216 5 Generalized Linear Models: Structure

Example 5.6. For the Poisson distribution, the results in Example 5.2 can be

used to obtain K(t)=μ(exp t − 1). 

5.3.5 The Mean and Variance of an EDM

The mean and variance of an edm are found by applying (5.8)to(5.5):

E[y]=μ =

dκ(θ)

dθ

and var[y]=φ

κ(θ)

dθ

. (5.9)

Observe that

κ(θ)

dθ



dκ(θ)

dθ



dμ

dθ

Since d

κ(θ)/dθ

> 0 is a variance, then dμ/dθ>0. This means that μ

must be a monotonically increasing function of θ,soμ and θ are one-to-one

functions of each other. Hence, deﬁne

V (μ)=

dμ

dθ

, (5.10)

called the variance function. Then the variance of y can be written as

var[y]=φV (μ). (5.11)

The variance is a product of the dispersion parameter φ and V (μ). Table 5.1

(p. 221) gives the variance function for common edms.

Example 5.7. For the normal distribution (Example 5.1; Table 5.1), κ(θ)=

/2, and so E[y]=dκ(θ)/dθ = θ. Since θ = μ for the normal distribution,

E[y]=θ = μ (as expected). For the variance, compute V (μ)=d

κ(θ)/dθ

1, and so var[y]=φV (μ)=σ

as expected. 

Example 5.8. For the Poisson distribution (Example 5.2; Table 5.1), κ(θ)=μ

and θ = log μ. The mean is

E[y]=

dκ

dθ

dκ

dμ

dθ

= μ

as expected. For the variance function, V (μ)=dμ/dθ = μ. Since φ =1for

the Poisson distribution, var[y]=μ for the Poisson distribution. 

5.3 The Random Component: Exponential Dispersion Models 217

5.3.6 The Variance Function

The variance function V (μ) uniquely determines the distribution within the

class of edms since the variance function determines κ(θ), up to an addi-

tive constant. This in turn speciﬁes K(t), which uniquely characterizes the

distribution.

To demonstrate, consider edms with V (μ)=μ

. Since V (μ)=dμ/dθ

from (5.10), solve dθ/dμ = μ

−2

for θ to obtain θ = −1/μ, setting the inte-

gration constant to zero. Then using that μ =dκ(θ)/dθ from (5.9) together

with θ = −1/μ shows that κ(θ)=−log(−θ) = log μ. Using these forms for θ

and κ(θ), the edm uniquely corresponding to V (μ)=μ

has the probability

function

P(y)=a(y, φ)exp



y(−1/μ) − log μ



for an appropriate normalizing function a(y; φ). The constants of integra-

tion are not functions of μ, so are absorbed into a(y, φ) if not set to zero.

This probability function is the probability function for a gamma distribu-

tion. Hence, the variance function V (μ)=μ

uniquely refers to a gamma

distribution within the edm class of distributions.

This result means that if the mean–variance relationship can be estab-

lished for a given data set, and quantiﬁed using the variance function, the

corresponding edm is uniquely identiﬁed.

In general, (5.11) states that, in general, the variance of an edm depends

on the mean. The normal distribution is unique in the family of edms, as its

variance does not depend on the mean since V (μ) = 1. For other edms, the

variance is a function of the mean, and the role of the variance function is to

specify exactly that function.

Example 5.9. For the noisy miner data [6] in Table 1.2 (data set: nminer),

divide the data into ﬁve approximately equal-sized groups:

> data(nminer)

> breaks <- c(-Inf, 4, 11, 15, 19, Inf) + 0.5 # Break points

> Eucs.cut <- cut(nminer$Eucs, breaks ); summary(Eucs.cut)

(-Inf,4.5] (4.5,11.5] (11.5,15.5] (15.5,19.5] (19.5, Inf]

96565

For each group, compute the mean and variance of the number of noisy

miners:

> mn <- tapply( nminer$Minerab, Eucs.cut, "mean" ) # Mean of each group

> vr <- tapply( nminer$Minerab, Eucs.cut, "var" ) # Var of each group

> sz <- tapply( nminer$Minerab, Eucs.cut, "length" ) # Num. in each group

> cbind("Group size"=sz, "Group mean"=mn, "Group variance"=vr)

Group size Group mean Group variance

(-Inf,4.5] 9 0.1111111 0.1111111

(4.5,11.5] 6 0.5000000 1.5000000

(11.5,15.5] 5 3.8000000 11.2000000

218 5 Generalized Linear Models: Structure

(15.5,19.5] 6 4.3333333 7.8666667

(19.5, Inf] 5 7.0000000 48.5000000

The command tapply(nminer$Minerab, Eucs.cut, "mean") computes

the mean() of nminer$Minerab for each level of Eucs.cut. More generally,

tapply(X, INDEX, FUN) applies the function FUN() to the data X,foreach

group of values in the unique combination of factors in INDEX.

A plot of the logarithm of each group mean against the logarithm of each

group variance (Fig. 5.1, right panel) shows that, in general, the variance

increases as the mean increases:

> plot(jitter(Minerab)~(Eucs), pch=1, las=1, data=nminer, ylim=c(0, 20),

xlab="Number of eucalypts/2 ha.", ylab="Number of noisy miners")

> # Draw the dashed vertical lines

> abline(v=breaks, lwd=1, lty=2, col="gray")

> plot( log( vr ) ~ log ( mn ), pch=19, las=1, cex=0.45*sqrt(sz),

xlab="Log of means", ylab="Log of variances" )

(The points are plotted so that the area is proportional to the sample size.

The scaling factor 0.45 is chosen by trial-and-error.) More speciﬁcally, an

approximate linear a relationship of the form

log(group variance) = a + b log(group mean)

may be reasonable (Fig. 5.1, right panel). This is equivalent to (group

variance) ∝ (group mean)

. This is the form of the variance of an edm:

var[y]=φV (μ), where V (μ)=μ

and where b is the slope of the linear

relationship:

> hm.lm <- lm( log( vr ) ~ log ( mn ), weights=sz )

> coef(hm.lm); confint(hm.lm)

(Intercept) log(mn)

0.802508 1.295222

2.5 % 97.5 %

(Intercept) 0.007812159 1.597204

log(mn) 0.821058278 1.769386

For the data, the slope of the linear regression line (weighted by the number

of observations in each group) is b ≈ 1.3, suggesting the mean is approxi-

mately proportional to the variance. In addition, the estimate of φ is approx-

imately 1 as needed for the Poisson distribution. In other words, V (μ)=μ

approximately. Since this is the variance function for a Poisson distribution

(Table 5.1), a Poisson distribution may be suitable for the data. Of course,

the Poisson distribution is also suggested because the data are counts. 

5.4 EDMs in Dispersion Model Form

5.4.1 The Unit Deviance and the Dispersion Model Form

We have shown that μ and θ are one-to-one functions of each another. As a

result, it must be possible to write the probability function (5.1) as a function

5.4 EDMs in Dispersion Model Form 219

0 5 10 15 20 25 30

Number of eucalypts/2 ha.

Number of noisy miners

−2 −1 0 1 2

−2

−1

Log of means

Log of variances

Fig. 5.1 Plots of the noisy miner data. Left: the number of noisy miners plotted against

the number of eucalypt trees (a small amount of randomness is added in the vertical

direction to the number of noisy miners to avoid over-plotted observations). The dashed

vertical lines break the data into ﬁve groups of similar size. Right panel: the logarithm

of sample variances for each group plotted against the logarithm of the sample means

for each group in the data; the area of the plotted points are proportional to the number

of observations in each group (Example 5.9)

of μ instead of θ. We will see that this version has some advantages because

μ has such a clear interpretation as the mean of the distribution. To do this,

start by writing

t(y, μ)=yθ − κ(θ)

for that part of the probability function which depends on θ. There must be

some function t(·, ·) for which this is true. Now consider t(y, μ) as a function

of μ. See that

∂t(y, μ)

∂θ

= y −

dκ(θ)

dθ

= y −μ

and

∂

t(y, μ)

∂θ

κ(θ)

dθ

= V (μ) > 0.

The second derivative is always positive, and the ﬁrst derivative is zero at

y = μ,sot(y, μ) must have a unique maximum with respect to μ at μ = y.

This allows us to deﬁne a very important quantity, the unit deviance:

d(y, μ)=2{t(y, y) − t(y, μ)}. (5.12)

Notice that d(y, μ) = 0 only when y = μ and otherwise d(y, μ) > 0. In fact,

d(y, μ) increases as μ moves away from y in either direction. This shows that

d(y, μ) can be interpreted as a type of distance measure between y and μ.

220 5 Generalized Linear Models: Structure

In terms of the unit deviance, the probability function (5.1) for an edm is

P(y; μ, φ)=b(y, φ)exp



−

2φ

d(y, μ)



, (5.13)

where b(y,φ)=a(y,φ)exp{t(y,y)/φ}, which cannot always be written in

closed form. This is called the dispersion model form of the probability func-

tion for edms, and is invaluable for much of what follows.

Example 5.10. For the normal distribution (Example 5.1), deduce that

t(y, μ)=yμ − μ

/2andsot(y,y)=y

− y

/2=y

/2. The unit dev-

iance then is d(y, μ)=(y − μ)

. Hence the normal distribution written

as (5.2) is in dispersion model form. 

The above deﬁnition for the unit deviance assumes that we can always set

μ equal to y. However, cases exist when values of y are not allowable values

for μ. The important cases occur when y is on the boundary of the support of

the distribution. For example, the binomial distribution requires 0 <μ<1,

so setting μ = y is not possible when y =0ory = 1. However μ can still take

values arbitrarily close to y. To cover these cases, we generalize the deﬁnition

of the unit deviance to

d(y, μ)=2

lim

→0

t(y + , y + ) − t(y, μ)

. (5.14)

If y is on the lower boundary of S, the right limit will be taken. If y is at

the upper bound (such as y = 1 for the binomial), then the left limit is

taken. This deﬁnition covers all the distributions considered in this book. For

simplicity, the unit deviance is usually written as (5.12), on the understanding

that (5.14) is used when necessary. The unit deviances for common edmsare

in Table 5.1 (p. 221).

Example 5.11. Consider the Poisson distribution in Example 5.2 (p. 213), for

which μ>0. Deduce that t(y, μ)=y log μ − μ.Ify = 0, then t(y, y)=

y log y − y,sothat

d(y, μ)=2



y log

− (y − μ)



. (5.15)

If y = 0 we need the limit form (5.14) of the unit deviance instead. It is easily

seen that lim

↓0

t(y + , y + )=0sothat

d(0,μ)=2μ. (5.16)

The unit deviance is commonly written as (5.15) on the understanding that

the limit form (5.16) is used when y = 0. The other terms in the dispersion

model form (5.13)areb(y)=(y log y − y)/y!andφ =1. 

As already noted, the unit deviance is a measure of the discrepancy be-

tween y and μ. For normal distributions, the unit deviance d(y, μ)=(y −μ)

(Example 5.10) is symmetric about μ as a function of y. For other edms, the

Tabl e 5.1 Common edms, showing their variance function V (μ), cumulant function κ(θ), canonical parameter θ, dispersion parameter φ, unit

deviance d(y, μ), support S (the permissible values of y), domain Ω for μ and domain Θ for θ. For the Tweedie distributions, the case ξ =2is

the gamma distribution, and ξ =1withφ = 1 is the Poisson distribution. R refers to the real line; N refers to the natural numbers 1, 2,...;

superscript + means positive values only; superscript − means negative values only; subscript 0 means zero is included in the space (Sect. 5.3.5)

edm V (μ) κ(θ) θφ d(y, μ) SΩΘReference

Normal 1 θ

/2 μσ

(y −μ)

RRRChaps. 2 and 3

Binomial μ(1 − μ)

exp θ

1+expθ

log

1 − μ

y log

+(1− y)log

1 − y

1 − μ

0, 1,...m

(0, 1) R Chap. 9

Negative

binomial μ +

−log(1 −exp θ)log

μ + k

y log

− (y + k)log

y + k

μ + k

−

Chap. 10

Poisson μ exp θ log μ 12

y log

− (y −μ)

R Chap. 10

Gamma μ

−log(−θ) −

φ 2

−log

y −μ

R Chap. 11

Inverse

Gaussian μ

−

√

−2θ −

2μ

(y −μ)

−

Chap. 11

Tweedie

(ξ ≤ 0orξ ≥ 1) μ

{(1 − ξ)θ}

(2−ξ)/(1−ξ)

2 − ξ

1−ξ

1 − ξ

φ 2



max(y, 0)

2−ξ

(1 − ξ)(2 −ξ)

− ξ<0: RR

Chap. 12

for ξ =2 forξ =1

yμ

1−ξ

1 − ξ

2−ξ

2 − ξ



1 <ξ<2: R

−

for ξ =1, 2 ξ>2: R

−

222 5 Generalized Linear Models: Structure

unit deviance is asymmetric (Fig. 5.2), because diﬀerences relative to the vari-

ance are important. For example, consider the unit deviance for the gamma

distribution (which has V (μ)=μ

) with μ = 3 (Fig. 5.2, bottom left panel).

The unit deviance is greater at y = 1 than at y = 5 even though the absolute

diﬀerence |y −μ| = 2 is the same in both cases. This is because the variance

is smaller at y = 1 than at y = 5, so the diﬀerence between y and μ is greater

in standard deviation terms.

Technical note. All the edm distributions used for examples in this book

have the property that the domain Ω for μ is the same as the support for y,

at least in a limiting sense. (Technically, the support for y is contained in the

closure of the domain for μ.) However, edms exist for which the allowable

values for μ are far more restricted than those for y. Chapter 12 will discuss

Tweedie models with power variance functions V (μ)=μ

. When ξ<0, the

resulting distributions can take all values y on the real line, whereas the mean

is restricted to be positive, μ>0. To cover such distributions, the deﬁnition

of the unit deviance can be generalized further to

0246

Unit deviance for

a normal EDM

The response y

Unit deviance d

(

μ)

01234567

Unit deviance for

a Poisson EDM

The response y

Unit deviance d(y,μ)

01234567

Unit deviance for

a gamma EDM

The response y

Unit deviance d(

)

Unit deviance for

a binomial EDM

The response y

Unit deviance

(y,μ)

0.0 0.2 0.4 0.6 0.8 1.0

Fig. 5.2 The unit deviance d(y, μ)forfouredms. Top left panel: the unit deviance for

the normal distribution when μ = 3; top right panel: the unit deviance for the Poisson

distribution when μ = 3; bottom left panel: the unit deviance for the gamma distribution

when μ =3andφ = 1; bottom right: the unit deviance for the binomial distribution

when μ =0.2. The solid points show where the limit form of the unit deviance (5.14)

has been used (Sect. 5.11)

5.4 EDMs in Dispersion Model Form 223

d(y, μ)=2



sup

μ∈Ω

t(y, μ) − t(y, μ)



(5.17)

where the notation ‘sup’ is short for ‘supremum’. However such distributions

do not have any useful applications for modelling real data, as least not yet,

so we can ignore this technicality in practice. The limiting deﬁnition (5.14)

given previously is adequate for all applications considered in this book.

5.4.2 The Saddlepoint Approximation

The saddlepoint approximation to the edm density function P(y; μ, φ) is de-

ﬁned by

P(y; μ, φ)=



2πφV (y)

exp



−

d(y, μ)

2φ



. (5.18)

The saddlepoint approximation is often remarkably accurate, even in the

extreme tails of the distribution. As well as being computationally useful

in some cases, the approximation aids our theoretical understanding of the

properties of edms.

For practical use, the term V (y) in the denominator of (5.18) is usually

modiﬁed slightly so that it can never take the value zero [7]. For example,

the saddlepoint approximation to the Poisson or negative binomial distribu-

tions can be improved by replacing V (y) with V (y + ) where  =1/6. The

saddlepoint approximation, adjusted in this way, has improved accuracy ev-

erywhere as well as having the advantage of being deﬁned at y = 0. This is

called the modiﬁed saddlepoint approximation.

Comparing to the dispersion model form (5.13)(p.220), the saddlepoint

approximation (5.18) is equivalent to writing b(y, φ) ≈ 1/



2πφV (y). Ob-

serve that b(y, φ), which for some edms isn’t available in any closed form, is

approximated by a simple analytic function.

Example 5.12. For the normal distribution, V (μ)=1sothatV (y)=1.

Applying (5.18) simply reproduces the probability function for the normal

distribution in dispersion model form (5.2). This shows that the saddlepoint

approximation is exact for the normal distribution. 

Example 5.13. For the Poisson distribution, V (μ)=μ so that V (y)=y.The

saddlepoint approximation is therefore

P(y; μ)=

√

2πy

exp{−y log(y/μ)+(y −μ)}. (5.19)



224 5 Generalized Linear Models: Structure

5.4.3 The Distribution of the Unit Deviance

The saddlepoint approximation has an important consequence. If the saddle-

point approximation to the probability function of an edm is accurate, then

it follows that the unit deviance d(y, μ) follows a χ

distribution.

To prove this, we use the fact that the χ

distribution is determined by

its mgf. Consider a random variable y whose probability function is an edm.

If the saddlepoint approximation to its probability function is accurate, then

the mgf of the unit deviance is

d(y,μ)

(t) = E[exp{d(y, μ)t}] (by deﬁnition)

exp{d(y, μ)t}



2πφV (y)

exp



−

d(y, μ)

2φ



dy.

(Recall that y ∈ S.) Rearranging:

d(y,μ)

(t)=

exp



−d(y, μ)



1 − 2φt

2φ





2πφV (y)

=(1− 2φt)

−1/2

(1 − 2φt)

1/2

{2πφV (y)}

1/2

exp



−d(y, μ)



1 − 2φt

2φ



dy.

Let φ



= φ/(1 − 2φt). Then

d(y,μ)

(t)=(1− 2φt)

−1/2

{2πφ



V (y)}

−1/2

exp



−

d(y, μ)

2φ





=(1− 2φt)

−1/2

, (5.20)

since the integrand is the (saddlepoint) density of the distribution with φ



φ/(1 − 2φt). The mgf (5.20) identiﬁes a χ

distribution, showing that

d(y, μ)/φ ∼ χ

(5.21)

whenever the saddlepoint approximation is accurate. This result forms the

basis of small-dispersion asymptotic theory used in Chap. 7. Note that (5.21)

implies that E[d(y,μ)] = φ whenever the saddlepoint approximation is accu-

rate.

Example 5.14. The saddlepoint approximation is exact for the normal dis-

tribution (Example 5.12), implying that the unit deviance has an exact

distribution for the normal distribution. The unit deviance for the nor-

mal distribution, found in Example 5.10,isd(y, μ)=(y − μ)

. This means

d(y, μ)/φ = {(y − μ)/σ}

, which deﬁnes a χ

random variate when y comes

from the N(μ, σ

) distribution. 

5.4 EDMs in Dispersion Model Form 225

5.4.4 Accuracy of the Saddlepoint Approximation

The saddlepoint approximation is exact for the normal and inverse Gaussian

distributions (Example 5.12; Problem 5.9). For other two-parameter distribu-

tions, the accuracy is such that

P(y; μ, φ)=P(y; μ, φ){1+O(φ)}, where O(φ)

means “order φ”, an expression which is like a constant times φ as φ → 0[3].

This shows that the error is relative, so that the density is approximated

equally well even in the tails of the distribution where the density is low.

This expression also shows that the approximation becomes nearly exact for

φ small.

For the gamma distribution, the saddlepoint approximation is equivalent

to approximating the gamma function Γ (1/φ) in the probability function

with Stirling’s formula

n! ≈ n

exp(−n)

√

2πn as n →∞. (5.22)

For the gamma distribution, the relative accuracy of the approximation is

constant for all y.

For the binomial, Poisson and negative binomial distributions, the saddle-

point approximation is equivalent to replacing all factorials in the probability

density functions with their Stirling’s formula equivalents. This means that

the saddlepoint approximation will be good for the Poisson distribution if y is

not too small. For the binomial distribution, the saddlepoint approximation

will be accurate if my and m(1 − y) are both not too small.

Smyth and Verbyla [11] give a guideline for judging when the saddlepoint

approximation is suﬃciently accurate to be relied on for practical purposes.

They deﬁne

τ =

φV (y)

(y −boundary)

, (5.23)

where “boundary” is the nearest boundary of the support S for y. Here τ is

a sort of empirical coeﬃcient of variation. Based on a number of heuristic

and theoretical justiﬁcations, they argue that the saddlepoint approxima-

tion should be adequate when τ ≤ 1/3. This corresponds to the following

guidelines (Problems 5.13 to 5.15):

• Binomial distribution: my ≥ 3andm(1 − y) ≥ 3.

• Poisson distribution: y ≥ 3.

• Gamma distribution: φ ≤ 1/3.

These guidelines apply to the ordinary saddlepoint approximation. The mod-

iﬁed saddlepoint approximation is often much better, sometimes adequate for

any y.

Comparing the saddlepoint approximation with the Central Limit Theo-

rem is revealing. It is true that edms converge to normality also as φ → 0,

a result which can be derived from the Central Limit Theorem. However,

the saddlepoint approximation is usually far more accurate, because its error

226 5 Generalized Linear Models: Structure

012345

0.00

0.05

0.10

0.15

0.20

0.25

0.30

Prob. function and saddlepoint

approx. for a Poisson EDM

Probability

Exact

Ordinary

Modified

012345

−2

Rel. error of saddlepoint

approx. for a Poisson EDM

Relative error (%)

Ordinary

Modified

Fig. 5.3 The accuracy of the saddlepoint approximation for the Poisson distribution

with μ =2.Fory = 0 the ordinary saddlepoint approximation is undeﬁned. The modiﬁed

saddlepoint is evaluated with  =1/6. The accuracy of the modiﬁed approximation is

never worse than 2.3% (Example 5.15)

is relative and O(φ), whereas the accuracy of the Central Limit Theorem is

additive and O(

√

φ ). This means that the saddlepoint approximation applies

for larger values of φ than the Central Limit Theorem. For continuous edms,

the saddlepoint approximation holds almost uniformly in the tails of the dis-

tribution, whereas the Central Limit Theorem is best near the mean of the

distribution and deteriorates rapidly in the tails.

Example 5.15. For the Poisson distribution, V (μ)=μ, so the modiﬁed sad-

dlepoint approximation is

P(y; μ)=



2π(y + )

exp{−y log(y/μ)+(y − μ)}.

The ordinary saddlepoint approximation (5.19) corresponds to  =0.Therel-

ative accuracy of the saddlepoint approximation is the same for any μ at given

y (Fig. 5.3, right panel). The relative accuracy of the ordinary approximation

is less than 3% when y ≥ 3. The accuracy of the modiﬁed approximation is

excellent, never worse than 2.3%. 

5.4.5 Accuracy of the χ

Distribution for the Unit

Deviance

In the previous section we considered conditions under which the saddlepoint

approximation to the probability function should be accurate. In this section,

5.4 EDMs in Dispersion Model Form 227

we consider what implications this has for the distribution of the unit dev-

iance. We have already noted that the relative accuracy of the saddlepoint

approximation does not depend on μ. However, when we consider the distri-

bution of the unit deviance, the saddlepoint approximation needs to hold for

all likely values of y. So we need μ and φ to be such that values of y close to

the boundary of the distribution are not too likely.

For the normal and inverse Gaussian distributions, the unit deviance has

an exact χ

distribution since the saddlepoint approximation is exact for

these distributions. For other edms, the distribution of the unit deviance

approaches χ

for any μ as φ → 0.

We will limit our investigation to considering how close the expected value

of the unit deviance is to its nominal value φ. For continuous distributions,

the expected value of the unit deviance is deﬁned by

E[d(y, μ)] =

d(y, μ)P(y; μ, φ) dy

where P(y; μ, φ) is the probability density function of the distribution. Using

this expression, the expected value of the unit deviance can be computed for

the gamma distribution, and compared to E[d(y, μ)] = φ (Fig. 5.4, top left

panel). The relative error is less than about 5% provided φ<1/3.

For discrete distributions, the expected value of the unit deviance is deﬁned

E[d(y, μ)] =



d(y, μ)P(y; μ, φ)

where P(y; μ, φ) is the probability mass function of the distribution. We now

use r to compute the expected value of the unit deviance for the Poisson

distribution, and compare it to its nominal value E[d(y,μ)] = 1 according to

the chi-square approximation (Fig. 5.4, top right panel):

> Poisson.mu <- c(0.000001, 0.001, 0.01, seq(0.1, 10, by=0.1) )

> DensityTimesDeviance <- function(mu) {

y <- seq(0, 100, by=1)

sum( dpois(y, lambda=mu) * poisson()$dev.resids(y, mu, wt=1) )

}

> ExpD.psn <- sapply( Poisson.mu, DensityTimesDeviance)

> plot( ExpD.psn ~ Poisson.mu, las=1, type="n",

main="Poisson distribution", xlab=expression(mu),

ylab="Exp. value of unit deviance")

> polygon( x=c(-1, -1, 12, 12), y=c(0.95, 1.05, 1.05, 0.95),

col="gray", border=NA) # Draws the region of 5% rel. accuracy

> lines( ExpD.psn ~ Poisson.mu, lty=2, lwd=2)

> abline(h=1)

(The awkward construct poisson()$dev.resids() accesses the function

dev.resids() from the poisson() family deﬁnition. Despite its name, dev.

resids() returns the unit deviance.) The plots show that the expected value

of the deviance is generally not near one for small μ, but the error is well

below 10% provided μ>3.

228 5 Generalized Linear Models: Structure

For the binomial distribution, plots of the expected value of the deviance

against μ for various values of m (Fig. 5.4, bottom panels) show that the

expected value of the deviance can be far from one when mμ or m(1 −μ)are

small, but the error is reasonable provided mμ > 3andm(1 − μ) > 3.

In summary, the unit deviance is always chi-square for the normal and

inverse Gaussian distributions, and for other common edms the unit deviance

is roughly chi-square with the correct expected value when

• Binomial distribution: mμ ≥ 3andm(1 − μ) ≥ 3.

• Poisson distribution: μ ≥ 3.

• Gamma distribution: φ ≤ 1/3.

0.0 0.1 0.2 0.3 0.4 0.5

0.0

0.1

0.2

0.3

0.4

0.5

Gamma distribution

Exp. value of unit deviance

E[d(y,μ)]

E[d(y,μ)] =φ

0246810

0.0

0.2

0.4

0.6

0.8

1.0

1.2

Poisson distribution

Exp. value of unit deviance

E[d(y,μ)]

E[d(y,μ)] = 1

0.0 0.2 0.4 0.6 0.8 1.0

0.6

0.8

1.0

1.2

1.4

Binomial distribution

Exp. value of unit deviance

m = 2

m = 5

m = 10

0.0 0.2 0.4 0.6 0.8 1.0

0.6

0.8

1.0

1.2

1.4

Binomial distribution

Exp. value of unit deviance

m = 15

m = 30

m = 100

Fig. 5.4 The expected value of the unit deviance (modelled on [12, p. 208]). Top left

panel: the gamma distribution for various values of φ (the solid line represents the target

E[d(y, μ)] = φ); top right panel: the Poisson distribution for various values of μ; bottom

panels: the binomial distribution for various values of μ and m. The gray regions indicate

relative accuracy within 5% (Sect. 5.4.5)

5.5 The Systematic Component 229

5.5 The Systematic Component

5.5.1 Link Function

In addition to assuming that the responses come from the edm family, glms

assume a speciﬁc form for the systematic component. Glms assume a sys-

tematic component where the linear predictor

η = β



j=1

is linked to the mean μ through a link function g() so that g(μ)=η. This

systematic component shows that glms are regression models linear in the

parameters.

The link function g(·) is a monotonic, diﬀerentiable function relating the

ﬁtted values μ to the linear predictor η. Monotonicity ensures that any value

of η is mapped to only one possible value of μ. Diﬀerentiability is required for

estimation (Sect. 6.2). The canonical link function is a special link function,

the function g(μ) such that η = θ = g(μ).

Example 5.16. For the normal distribution, θ = μ (Table 5.1,p.221). The

canonical link function is the identity link function g(μ)=μ, which implies

η = μ. 

Example 5.17. For the Poisson distribution, θ = log μ (Table 5.1,p.221).

The canonical link function is g(μ) = log μ,sothatlogμ = η. The Poisson

distribution is only deﬁned for positive values of μ, and the logarithmic link

function ensures η (which possibly takes any real value) always maps to a

positive value of

μ. Hence the canonical link function is a sensible link function

to use in this case. 

5.5.2 Oﬀsets

In some applications, the linear predictor contains a term that requires no

estimation, which is called an oﬀset. The oﬀset can be viewed as a term β

in the linear predictor for which β

is known a priori. For example, consider

modelling the annual number of hospital births in various cities to facilitate

resource planning. The annual number of births is discrete, so a Poisson

distribution may be appropriate. However, the expected annual number of

births μ

in city i depends on the given populations P

of the city, since cities

with larger population would be expected to have more births each year, in

230 5 Generalized Linear Models: Structure

general. The number of births per unit of population, assuming a logarithmic

link function, can be modelled using the systematic component

log(μ/P )=η,

for the linear predictor η. Rearranging to model μ:

log(μ) = log P + η.

The ﬁrst term in the systematic component log P is completely known: noth-

ing needs to be estimated. The term log P is called an oﬀset. Oﬀsets com-

monly appear in Poisson glms, but may appear in any glm (Example 5.18).

The oﬀset variable is commonly a measure of exposure. For example, the

number of cases of a certain disease recorded in various mines depends on the

number of workers, and also on the number of years each worker has worked

in the mine. The exposure would be the number of person-years worked in

each mine, which could be incorporated into a glm as an oﬀset. That is, a

mine with many workers who have been employed for many years would be

exposed to a greater likelihood of a worker contracting the disease than a

mine with only a few workers who have been employed for short periods of

time.

Example 5.18. For the cherry tree data (Example 3.14,p.125), approximat-

ing the shape of the trees as a cone or as a cylinder leads to a model with

the systematic component

log μ = β

+ 2 log g + log h, (5.24)

where g is the girth and h is the height of each tree, and the value of β

diﬀerent for cones and cylinders. To ﬁt this model, the term 2 log g + log h is

an oﬀset, as this expression has no terms requiring estimation. 

5.6 Generalized Linear Models Deﬁned

The two components of a generalized linear model (glm) have been discussed:

the random component (Sect. 5.3) and the systematic component (Sect. 5.5).

Now a glm can be formally deﬁned. A glm consists of two components:

• Random component: The observations y

come independently from a

speciﬁed edm such that y

∼ edm(μ

,φ/w

)fori =1, 2,...,n.Thew

are known non-negative prior weights, which potentially weight each Ob-

servation i diﬀerently. Commonly, the prior weights all equal one.

• Systematic component: A linear predictor η

= o

+ β



j=1

where the o

are oﬀsets (Sect. 5.5.2) that are often equal to zero, and

g(μ)=η is a known, monotonic, diﬀerentiable link function.

5.7 The Total Deviance 231

The glm is

⎧

⎪

⎨

⎪

⎩

∼ edm(μ

,φ/w

)

g(μ

)=o

+ β



j=1

(5.25)

The core structure of a glm is speciﬁed by the choice of distribution from

the edm class and the choice of link function; that is, the answer to the two

important questions in Sect. 5.2. The notation

glm(edm; Link function)

speciﬁes the glm by giving the edm used for the random component, and

the link function relating the mean μ to the explanatory variables.

Example 5.19. For the Quilpie rainfall data (Example 4.6,p.174), the model

suggested is



∼ Bin(μ

) (random component)

log

1 − μ

= β

+ β

(systematic component)

where x

is the soi,andy

= 1 if the total July rainfall exceeds 10 mm

(and y

= 0 otherwise). This is a binomial glm. Algorithms for estimat-

ing the values of β

and β

arediscussedinChap.6.Theglm is denoted

glm(binomial; logit). In r,theglm is speciﬁed by family("binomial",

link="logit"). 

5.7 The Total Deviance

The unit deviance has been shown to be a measure of distance between y and

μ (Sect. 5.4.1). An overall measure of the distance between all the y

and all

the μ

can be deﬁned as

D(y,μ)=



i=1

d(y

,μ

called the deviance function, and its value called the deviance or the total

deviance.Thescaled deviance function is deﬁned as

∗

(y, μ)=D(y, μ)/φ,

and its value is called the scaled deviance or the scaled total deviance.

232 5 Generalized Linear Models: Structure

If the saddlepoint approximation holds, then the distribution of the scaled

deviance follows an approximate chi-square distribution

∗

(y, μ) ∼ χ

with μ

(for all i)andφ at their true values. As usual, the approximation is

exact for normal linear glms. However, in practice the μ

are seldom known.

We will return to the distribution of the deviance and scaled deviance func-

tions when the β

are estimated in Chap. 7.

Note that by using the dispersion model form of the edm, the log-likelihood

function for the glm in (5.25) can be expressed as

(μ; y)=



i=1

log b(y

,φ/w

) −

2φ



i=1

d(y

,μ

)



i=1

log b(y

,φ/w

) −

D(y,μ)

2φ

. (5.26)

Example 5.20. For a normal linear glm, y

∼ N(μ

,σ

) (Example 5.10), and

D(y,μ)=



i=1

− μ

)

. This is the squared Euclidean distance between

the corresponding values of y

and μ

. Hence, D

∗

(y, μ)=



i=1

{(y

−μ

)/σ}

which has an exact χ

distribution. 

5.8 Regression Transformations Approximate GLMs

In Chap. 3, variance-stabilizing transformations of y were used to create con-

stant variance in the response for linear regression models. When V (μ) rep-

resents the true mean–variance relationship for the responses, there is a clear

relationship between V (μ) and the variance-stabilizing transformation. Con-

sider the transformation y

∗

= h(y). A ﬁrst-order Taylor series expansion

about μ gives h(y) ≈ h(μ)+h



(μ)(y −μ), so that

var[y

∗

]=var[h(y)] ≈ h



(μ)

var[y].

Hence the transformation y

∗

= h(y) will approximately stabilize the vari-

ance (that is, ensure var[y

∗

] is approximately constant) if h



(μ) is propor-

tional to var[y]

−1/2

= V (μ)

−1/2

. Using linear regression after a transforma-

tion of y is therefore roughly equivalent to ﬁtting a glm with variance func-

tion V (μ)=1/h



(μ)

and link function g(μ)=h(μ). Almost any variance-

stabilizing transformation can be viewed in this way (Table 5.2). Notice that

the choice of transformation h(y) inﬂuences both the implied variance func-

tion (and hence edm) and the implied link function.

5.8 Regression Transformations Approximate GLMs 233

Tabl e 5.2 edms and the approximately equivalent variance-stabilizing transformations

used with linear regression models (Sect. 5.8)

Variance-stabilizing

transformation

The glm being approximated

(with Box–Cox λ) Variance function Link function

∗

=sin

−1

√

yV(μ)=μ(1 − μ) g(μ)=sin

−1

√

Binomial glm (Chap. 9)

∗

√

y (λ =0) V (μ)=μg(μ)=

√

Poisson glm (Chap. 10)

∗

=logy (λ =0) V (μ)=μ

g(μ)=logμ

gamma glm (Chap. 11)

∗

=1/

√

y (λ = −1/2) V (μ)=μ

g(μ)=1/

√

inverse Gaussian (Chap. 11)

∗

=1/y (λ = −1) V (μ)=μ

g(μ)=1/μ

Tweedie glm,withξ = 4 (Chap. 12)

Example 5.21. Consider the square root transformation of the response, when

used in a linear regression model. Expanding this transformation about μ us-

ing a Taylor series gives var[

√

y ] ≈ var[y]/(4μ). This will be constant if var[y]

is proportional to μ, which is true if y follows a Poisson distribution. Using

this transformation of y in a linear regression model is roughly equivalent to

ﬁtting a Poisson glm with square root link function. 

Using a transformation to simultaneously achieve linearity and constant

variance assumes a relationship between the variance and link functions which

in general is overly simplistic. Glms obviously provide more ﬂexibility: glms

allow the edm family and link function to be chosen separately depending on

the data. The edm family is chosen to reﬂect the support of the data and the

mean–variance relationship, then the link function is chosen to achieve lin-

earity. Glms have the added advantages of modelling the data on the original

scale, avoiding artiﬁcial transformations, and of giving realistic probability

statements when the data are actually non-normal. The normal approxima-

tion for h(y), implicit in the transformation approach, is often reasonable

when φ is small, but may be very poor otherwise.

A glm enables the impact of the explanatory variables on μ to be inter-

preted directly. For example, consider a systematic component of glm using

a log-link:

log μ = β

+ β

which can be written as

μ =exp(β

)exp(β

)

234 5 Generalized Linear Models: Structure

However, a logarithmic transformation used with a linear regression model

gives

E[log y]=β

+ β

which does not allow direct interpretation in terms of μ =E[y]. However,

since E[log y] ≈ log E[y] = log μ (Problem 2.11), then

μ ≈ exp(β

)exp(β

)

5.9 Summary

Chapter 5 introduced the components, structure, notation and terminology

of generalized linear models. Glms are regression models linear in the param-

eters, and consist of two components (a random component and a systematic

component), chosen in separate decisions (Sect. 5.2).

Common distributions that are edms include the normal, Poisson, gamma,

binomial and negative binomial distributions (Sect. 5.3.1). The probability

function for edms has the general form (Sect. 5.3.2)

P(y; θ, φ)=a(y,φ)exp{[yθ − κ(θ)]/φ}

where θ is the called canonical parameter, κ(θ) is called the cumulant

function,andφ>0isthedispersion parameter. The moment generat-

ing function and cumulant generating function for an edm have simple

forms (Sect. 5.3.4), which can be used to show that the mean of an edm is

E[y]=μ =dκ/dθ (Sect. 5.3.5), and the variance of an edm is var[y]=φV (μ),

where V (μ)=d

κ(θ)/dθ

is the variance function (Sect. 5.3.5). The vari-

ance function uniquely determines the distribution within the class of edms

(Sect. 5.3.6).

The unit deviance is d(y,μ)=2{t(y, y) − t(y,μ)} (Sect. 5.4). Using this,

the dispersion model form of an edm is (Sect. 5.4)

P(y; μ, φ)=b(y, φ)exp



−

d(y, μ)

2φ



For edms, the saddlepoint approximation is

P(y; μ, φ)=



2πφV (y)

exp



−

d(y, μ)

2φ



The approximation is accurate as φ → 0 (Sect. 5.4.2). The saddlepoint ap-

proximation implies d(y, μ) ∼ χ

as φ → 0 (Sect. 5.4.3). The approximation

is exact for the normal and inverse Gaussian distributions (Sect. 5.4.3).

The link function g(·) expresses the functional relationship between the

mean μ and the linear predictor η as g(μ)=η = β



j=1

, where g(μ)

5.9 Summary 235

is a diﬀerentiable, monotonic function (Sect. 5.5.1). Oﬀsets are components

of the linear predictor with no unknown parameters (Sect. 5.5.2).

A glm is deﬁned by two components (Sect. 5.6):

• Random component: Observations y

come independently from an edm

such that y

∼ edm(μ

,φ/w

)fori =1, 2,...,n, where the w

are non-

negative prior weights.

• Systematic component: A link function g(·) such that g(μ

)=o

+ β



j=1

, where g(·) is a known, monotonic, diﬀerentiable link function

and o

is the oﬀset.

The core structure of a glm is denoted glm(edm; Link function) (Sect. 5.6).

The deviance function, a measure of total discrepancy between all the y

and μ

,isD(y, μ)=



i=1

d(y

,μ

). By the saddlepoint approximation,

D(y,μ)/φ ∼ χ

as φ → 0 (Sect. 5.7). The unit deviance has a chi-square

distribution for the normal and inverse Gaussian distributions (Sect. 5.4.5),

and is approximately distributed as chi-square with the correct expected value

when:

• Binomial distribution: mμ ≥ 3andm(1 − yμ) ≥ 3.

• Poisson distribution: μ ≥ 3.

• Gamma distribution: φ ≤ 1/3.

Variance-stabilizing transformations h(y) used with linear regression mod-

els are roughly equivalent to ﬁtting a glm with variance function V (μ)=

1/h



(μ)

and link function g(μ)=h(μ) (Sect. 5.8).

Problems

Selected solutions begin on p. 536.

5.1. Determine which of the following distributions are edms by identifying

(where possible) θ, κ(θ)andφ:

1. The beta distribution:

P(y; a, b)=

Γ (a + b)

Γ (a)Γ (b)

a−1

(1 − y)

b−1

for 0 <y<1, a>0andb>0, where Γ (·) is the gamma function.

2. The geometric distribution:

P(y; p)=p(1 − p)

y−1

(5.27)

for y =1, 2,... and 0 <p<1.

236 5 Generalized Linear Models: Structure

3. The Cauchy distribution:

P(y; c, s)=

πs



y−c



(5.28)

for −∞ <y<∞, −∞ <c<∞,ands>0.

4. The von Mises distribution, used for modelling angular data:

P(y; μ, λ)=

2πI

(λ)

exp{λ cos(y −μ)},

for 0 ≤ y<2π,0≤ μ<2π and λ>0, where I

(·) is the modiﬁed Bessel

function of order 0.

5. The strict arcsine distribution [5] used for modelling count data:

P(y; p)=A(y;1)

exp(−arcsin p),

for y =0, 1,... and 0 <p<1, where A(y; 1) is a complicated normalising

function.

5.2. Use the results E[y]=κ



(θ)andvar[y]=φκ



(θ) to ﬁnd the mean,

variance and variance function for the distributions in Problem 5.1 that are

edms.

5.3. Determine the canonical link function for the distributions in Prob-

lem 5.1 that are edms.

5.4. Use the deﬁnition of K(t)andM (t) to prove the following results.

1. Show that dK(t)/dt evaluated at t = 0 is the mean of y.

2. Show that d

K(t)/dt

evaluated at t = 0 is the variance of y.

5.5. Prove the result in (5.4), that κ

κ(θ)/dθ

for edms.

5.6. Show that the mean and variance of a discrete edm are given by E[y]=



(θ)andvar[y]=φκ



(θ) respectively by following similar steps as shown in

Sect. 5.3.5, but using summations rather than integrations.

5.7. For edms in the form of (5.1), show that the variance is var[y]=φκ



(θ)

by using the cgf (5.7).

5.8. Consider the gamma distribution, whose probability function is usually

written as

P(y; α, β)=

Γ (α)β

α−1

exp(−y/β)

for y>0 with α>0 (the shape parameter) and β>0 (the scale parameter),

where Γ (·) is the gamma function.

5.9 Summary 237

1. Show that the gamma distribution is an edm by identifying θ, κ(θ)and

φ.

2. Show that the saddlepoint approximation applied to the gamma distri-

bution is equivalent to using Stirling’s formula (5.22).

3. Determine the canonical link function.

4. Deduce the unit deviance for the gamma distribution.

5. Write the probability function in dispersion model form (5.13).

5.9. Consider the inverse Gaussian distribution, which has the probability

function

P(y; μ, φ)=(2πy

φ)

−1/2

exp



−

2φ

(y −μ)

yμ



where y>0, μ>0andφ>0.

1. Show that the inverse Gaussian distribution is an edm by identifying θ,

κ(θ)andφ.

2. Show that the variance function is V (μ)=μ

3. Determine the canonical link function.

4. Deduce the unit deviance and the deviance function.

5. Show that the saddlepoint approximation is exact for the inverse Gaus-

sian distribution.

5.10. Prove the results in Table 5.2 (p. 233). For example, show that the

variance-stabilizing transformation 1/

√

y used in a linear regression model

is approximately equivalent to using an inverse Gaussian glm with the link

function η =1/

√

μ. (Use a Taylor series expanded about the mean μ,asin

Sect. 5.8,p.232.)

5.11. Consider the Conway–Maxwell–Poisson (cmp) distribution [8], which

has the probability function

P(y; λ; ν)=

Z(λ, ν)(y!)

where y =0, 1, 2,..., λ>0, ν ≥ 0, and Z(λ, ν)=



∞

k=0

/(k!)

. (When

ν =0,thecmp distribution is undeﬁned for λ ≥ 1.)

1. Show that the cmp distribution is an edm with φ = 1 by identifying θ

and κ(θ), provided ν is known.

2. When ν is known, show that

μ =E[y]=

Z(λ, ν)

∞



k=0

kλ

(k!)

and var[y]=

Z(λ, ν)

∞



k=0

(k!)

− μ

3. Show that the cmp distribution allows for a non-linear decrease in suc-

cessive probabilities:

P(y −1; λ, ν)

P(y; λ, ν)

238 5 Generalized Linear Models: Structure

4. Show that ν = 1 corresponds to the Poisson distribution. (Hint:Use

that



∞

i=0

/i! = exp x.)

5. Show that ν = 0 corresponds to the geometric distribution (5.27) when

λ<1 and the probability of success is 1 −λ.(Hint: Use that



∞

i=0

1/(1 − x) provided |x| < 1.)

6. Show that ν →∞corresponds to the Bernoulli distribution (4.5) with

mean proportion λ/(1 + λ).

5.12. As in Fig. 5.3, compute the relative error in using the saddlepoint and

modiﬁed saddlepoint approximations for a Poisson distribution with μ =2.

Then, repeat the calculations for another value of μ,sayμ =4,andshow

that the relative error in the saddlepoint approximations are the same for

both values of μ (to computer precision).

5.13. Using (5.23), show that the saddlepoint approximation is expected to

hold for the Poisson distribution when y ≥ 3.

5.14. Using (5.23), show that the saddlepoint approximation is expected to

hold for the binomial distribution when my ≥ 3andmy(1 − y) ≥ 3.

5.15. Using (5.23), show that the saddlepoint approximation is expected to

hold for the gamma distribution when φ ≤ 1/3.

5.16. The probability function for a Poisson distribution is given in Exam-

ple 5.2 (p. 213).

1. Show that the mgf for the Poisson distribution is M(t) = exp(−μ + μe

(Hint: Use that exp x =



∞

i=0

/i!.)

2. Hence compute the cgf for the Poisson distribution.

3. Conﬁrm that the mean and the variance of the Poisson distribution are

both μ by using the cgf.

5.17. Suppose y

,...,y

are independently and identically distributed as

edm(μ, φ). Show that ¯y has the distribution edm(μ, φ/n) as follows.

1. Show that the cgf of ¯y is nK

(t/n), where K

(t)isthecgf of y.

2. By substituting the cgf of y into the resulting expression, show that the

cgf of ¯y is n {κ(θ + tφ/n) − κ(θ)}/φ.

3. Show that this cgf is the cgf for an edm(μ, φ/n) distribution.

5.18. Consider the edm with variance function V (μ)=1+μ

(the generalized

hyperbolic secant distribution [3]), which is deﬁned for all real y and all real μ.

1. Find the canonical form (5.1) of the density function for this distribution.

The normalizing constant a(y, φ) is diﬃcult to determine in closed form

but it is not necessary to do so.

2. Find the unit deviance for the edm.

3. Write down the saddlepoint approximation to the probability function.

5.9 Summary 239

4. Use r to plot the saddlepoint approximation to the probability function

for φ =0.5andφ = 1 when μ = −1. Do you expect the saddlepoint

approximation to be accurate? Explain.

5. Find the canonical link function.

5.19. Consider the edm with variance function V (μ)=μ

, which is deﬁned

for all real y>0 and all real μ>0.

1. Find the canonical form (5.1) of the density function for this distribution.

The normalizing constant a(y, φ) is diﬃcult to determine in closed form

but it is not necessary to do so.

2. Use that κ(θ) < ∞ to show that θ ≤ 0.

3. Find the unit deviance for the edm.

4. Write down the saddlepoint approximation to the probability function.

5. Use r to plot the saddlepoint approximation to the probability function

for φ =0.5andφ = 1 when μ =2.

6. Find the canonical link function.

5.20. Prove that the canonical link function and the variance function are

related by V (μ)=1/g



(μ)=dμ/dη, where g(μ) here is the canonical link

function.

5.21. Consider the expressions for the deviance function of the normal and

gamma distributions (Table 5.1,p.221). Show that if each datum y

is re-

placed by 100y

(say a change of measurement units from metres to cen-

timetres) that the numerical value of the gamma deviance function does not

change, but the numerical value of the normal deviance function changes.

5.22. The probability function for a special case of the exponential distribu-

tion is P(y) = exp(−y)fory>0.

1. Show that the mgf for this distribution is M(t)=(1− t)

−1

if t<1.

2. Hence compute the cgf for this distribution.

3. Conﬁrm that the mean and the variance of this distribution are both 1

by diﬀerentiating the cgf.

5.23. Consider a random variable y with the probability function P(y)=

y exp(−y)fory>0.

1. Show that the mgf for the distribution is M(t)=(1− t)

−2

if t<1.

2. Hence compute the cgf for the distribution.

3. Conﬁrm that the mean and the variance of this distribution are both 2

by diﬀerentiating the cgf.

5.24. Determine which of these functions are suitable link functions for a

glm. For those that are not suitable, explain why not.

1. g(μ)=−1/μ

when μ>0.

2. g(μ)=|μ| when −∞ <μ<∞.

240 REFERENCES

Tabl e 5 .3 The ﬁrst six observations of the Nambeware products data (Problem 5.26)

Diameter Grinding and polishing Price

Item (in inches) time (in min) ($US)

Casserole dish 10.7 47.65 144.00

Casserole dish 14.0 63.13 215.00

Casserole dish 9.0 58.76 105.00

Bowl 8.0 34.88 69.00

Dish 10.0 55.53 134.00

Casserole dish 10.5 43.14 129.00

3. g(μ) = log μ when μ>0.

4. g(μ)=μ

when −∞ <μ<∞.

5. g(μ)=μ

when 0 <μ<∞.

5.25. Children were asked to build towers as high as they could out of cubical

and cylindrical blocks [2, 9]. The number of blocks used and the time taken

were recorded (Table 2.12; data set: blocks). In this problem, only consider

the number of blocks used y and the age of the child x.

1. Plot the number of blocks used against the age of the child.

2. From the plot and an understanding of the data, answer the two questions

in Sect. 5.2 (p. 211) for these data, and hence propose a glm for the data.

5.26. Nambe Mills, Santa Fe, New Mexico [1, 10], is a tableware manufac-

turer. After casting, items produced by Nambe Mills are shaped, ground,

buﬀed, and polished. In 1989, as an aid to rationalizing production of its 100

products, the company recorded the total grinding and polishing times and

the diameter of each item (Table 5.3; data set: nambeware). In this problem,

only consider the item price y and the item diameter x.

1. Plot the price against diameter.

2. From the plot and an understanding of the data, argue that the answer

to the two questions in Sect. 5.2 (p. 211) may suggest a gamma glm.

References

[1] Data Desk: Data and story library (dasl) (2017). URL http://dasl.

datadesk.com

[2] Johnson, B., Courtney, D.M.: Tower building. Child Development 2(2),

161–162 (1931)

[3] Jørgensen, B.: The Theory of Dispersion Models. Monographs on Statis-

tics and Applied Probability. Chapman and Hall, London (1997)

REFERENCES 241

[4] Keller, D.K.: The Tao of Statistics: A Path to Understanding (with no

Math). Sage Publications, Thousand Oaks, CA (2006)

[5] Kokonendji, C.C., Khoudar, M.: On strict arcsine distribution. Commu-

nications in Statistics—Theory and Methods 33(5), 993–1006 (2004)

[6] Maron, M.: Threshold eﬀect of eucalypt density on an aggressive avian

competitor. Biological Conservation 136, 100–107 (2007)

[7] Nelder, J.A., Pregibon, D.: An extended quasi-likelihood function.

Biometrika 74(2), 221–232 (1987)

[8] Shmueli, G., Minka, T.P., Kadane, J.B., Borle, S., Boatwright, P.: A use-

ful distribution for ﬁtting discrete data: Revival of the Conway–Maxwell–

Poisson distribution. Journal of the Royal Statistical Society: Series C

54(1), 27–142 (2005)

[9] Singer, J.D., Willett, J.B.: Improving the teaching of applied statistics:

Putting the data back into data analysis. The American Statistician

44(3), 223–230 (1990)

[10] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

[11] Smyth, G.K., Verbyla, A.P.: Adjusted likelihood methods for modelling

dispersion in generalized linear models. Environmetrics 10, 695–709

(1999)

[12] Venables, W.N., Ripley, B.D.: Modern Applied Statistics with S, fourth

edn. Springer-Verlag, New York (2002). URL http://www.stats.ox.ac.

uk/pub/MASS4

Chapter 6

Generalized Linear Models:

Estimation

The challenge for the model builder is to get the most out

of the modelling process by choosing a model of the right

form and complexity so as to describe those aspects of the

system which are perceived as important.

Chatﬁeld [1, p. 27]

6.1 Introduction and Overview

The previous chapter deﬁned glms and studied the components of a glm.

This chapter discusses the estimation of the unknown parameters in the glm:

the regression parameters and possibly the dispersion parameter φ. Because

glms assume a speciﬁc probability distribution for the responses from the

edm family, maximum likelihood estimation procedures (Sect. 4.4) are used

for parameter estimation, and general formulae are developed for the glm

context. We ﬁrst derive the score equations and information for the glm con-

text (Sect. 6.2), which are used to form algorithms for estimating the regres-

sion parameters for glms (Sect. 6.3). The residual deviance is then deﬁned

as a measure of the residual variability across n observations after ﬁtting

the model (Sect. 6.4). The standard errors of the regression parameters are

developed in Sect. 6.5. In Sect. 6.6, matrix formulations are used to estimate

the regression parameters. We then explore the important connection between

the algorithms for ﬁtting linear regression models and glms (Sect. 6.7). Tech-

niques are then developed for estimating φ (Sect. 6.8). We conclude with a

discussion of using r to ﬁt glms (Sect. 6.9).

6.2 Likelihood Calculations for β

6.2.1 Diﬀerentiating the Probability Function

We begin by considering a single observation y ∼ edm(μ, φ/w), with prob-

ability function P(y; μ, φ/w). The probability function can be diﬀerentiated

easily, using its canonical form (5.1), as

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_6

243

244 6 Generalized Linear Models: Estimation

∂ log P(y; μ, φ/w)

∂θ

w(y − μ)

after substituting μ =dκ(θ)/dθ. Therefore

∂ log P(y; μ, φ/w)

∂μ

∂ log P(y; μ, φ/w)

∂θ

dθ

dμ

(6.1)

w(y − μ)

φV (μ)

, (6.2)

because dμ/dθ =d

κ(θ)/dθ

= V (μ). The simple form of this derivative

underlies much of glm theory.

Now suppose that

g(μ)=η = o +



j=0

, (6.3)

writing x

= 1 as the covariate for β

, and where o is the oﬀset. The deriva-

tives of log P(y; μ, φ/w) with respect to the β

are

∂ log P(y; μ, φ/w)

∂β

∂ log P(y; μ, φ/w)

∂μ

∂β

=(y −μ)

φV (μ)dη/dμ

. (6.4)

To ﬁnd the expected second derivatives, use the product rule to obtain

∂

log P(y; μ, φ/w)

∂β

∂

∂β

(y−μ)

φV (μ)

dη/dμ

+(y−μ)

∂

∂β



φV (μ)

dη/dμ



The second term has expectation zero because of the factor (y − μ), so



∂

log P(y; μ, φ/w)

∂β



= −

φV (μ)

(dη/dμ)

. (6.5)

Again, this is a very simple expression.

6.2.2 Score Equations and Information for β

Now consider a glm in which y

∼ edm(μ

,φ/w

) for observations y

,...,y

with the linear predictor in (6.3). The linear predictor contains p



unknown

regression parameters β

which need to be estimated from the data. Our

approach is to estimate the β

using maximum likelihood, using the techniques

in Sect. 4.4. To this end, we need to ﬁnd the ﬁrst and second derivatives of

the log-likelihood.

6.3 Computing Estimates of β 245

The log-likelihood function is

(β

,...,β

,φ; y)=



i=1

log P(y

; μ

,φ/w

From (6.4), the log-likelihood derivatives (score functions) are

U(β

∂(β

,...,β

,φ; y)

∂β



i=1

dη

dμ

− μ

(6.6)

where, for later convenience,

V (μ

)(dη

/dμ

)

. (6.7)

Equation (6.6) holds for j =0,...,p if we deﬁne x

= 1 as the covariate for

.TheW

are called the working weights.

From (6.5), the Fisher information for the regression parameters has ele-

ments

(β)=



i=1

. (6.8)

Example 6.1. Consider a Poisson glm using a logarithmic link function

log μ = η, with all prior weights w set to one. For the Poisson distribution,

V (μ)=μ and φ =1,sodη/dμ =1/μ and W = μ. Using (6.6) and (6.8), the

score function and Fisher information are, respectively

U(β



i=1

− μ

and I

(β)=



i=1



6.3 Computing Estimates of β

The Fisher scoring algorithm (Sect. 4.8,p.186) provides a convenient and

eﬀective method for computing the mlesoftheβ

The mlesoftheβ

, denoted

, are the simultaneous solutions of the p



score equations U(β

)=0forj =0,...,p. The scoring algorithm computes

the

by iteratively reﬁning the working estimates until convergence. Each

iteration consists of solving an equation involving the score function U(β

)

and the information I

(β).

246 6 Generalized Linear Models: Estimation

For convenience, deﬁne the working responses as

= η

dη

dμ

− μ

). (6.9)

It can be shown that each iteration of the scoring algorithm is equivalent

to least squares regression of the working responses z

on the covariates x

using the working weights W

(6.7). That is, z

is regressed onto x

using W

as the weights.

At each iteration, the z

and W

are updated, and the regression is repeated

to obtain new working coeﬃcients

(r)

(the estimate of β

at iteration r). The

linear predictor η

is updated from the working coeﬃcients, these are used to

update the ﬁtted values μ

= g

−1

(η

), then the iteration is repeated. Because

the working weights change at each iteration, the algorithm is often called

iteratively reweighted least squares (irls).

Importantly, φ doesn’t appear in the scoring iteration for the β

,sothere

is no need to know φ to estimate the β

. Because of this, estimation of φ is

deferred to Sect. 6.8.

Another important aspect of the scoring iteration is that the working re-

sponses z

and working weights W

depend on the working coeﬃcient esti-

mates

(r)

only through the ﬁtted values μ

. This allows the scoring algorithm

to be initialized using the responses y

. The aim of the modelling is to pro-

duce estimates ˆμ

as close as possible to the observations y

, so the algorithm

is started by setting initial values ˆμ

(0)

= y

. Sometimes a slight adjustment is

needed to avoid taking logarithms or reciprocals of zero, so ˆμ

(0)

= y

+0.1or

similar is used when ˆμ

(0)

would otherwise be zero. Binomial glmshaveprob-

lems when μ =0orμ = 1, so the algorithm starts using (my +0.5)/(m + 1).

The algorithm usually converges quite rapidly from these starting values.

Example 6.2. In Example 5.9 (data set: nminer), a Poisson glm is suggested

for the noisy miner data [4] with systematic component log μ = β

+ β

where x is number of eucalypts per 2 ha transect Eucs. Using the results from

Example 6.1 (p. 245),

z = log ˆμ +

y − ˆμ

ˆμ

. (6.10)

Solutions are found by regressing z on x using the weights W (using W = μ

as deﬁned in Example 6.1). The iterative solution is found by iterating (6.9).

We cannot start the algorithm by setting ˆμ = y because the data contain

cases where y = 0. Setting ˆμ = y in those cases would result in computing

the logarithms of zero and diving by zero in (6.10). For this reason, the

algorithm starts by using ˆμ = y +0.1. The working weights W and working

values z are computed and hence initial estimates of β

and β

are obtained.

Initially, the algorithm starts with the values in Table 6.1. The estimates are

6.3 Computing Estimates of β 247

Tabl e 6. 1 Starting the iterations for ﬁtting the Poisson glm to the noisy miner data.

Note that the algorithm starts with ˆμ = y +0.1 to avoid dividing by zero and taking

logarithms of zero (Example 6.2)

Case Observations Fitted values Working values Working weights

iy ˆμ

(0)

z =ˆη +(y − ˆμ)/ˆμW=ˆμ

10 0.10 −3.303 0.10

20 0.10 −3.303 0.10

33 3.10 1.099 3.10

42 2.10 0.6943 2.10

58 8.10 2.080 8.10

Tabl e 6. 2 Fitting the Poisson glm to the noisy miner data; the iterations have con-

verged to six decimal places (Example 6.2)

Iteration r Constant

(r)

D(y, μ

(r)

)

10.122336 0.081071 82.146682

2 −0.589798 0.103745 64.495148

3 −0.851982 0.113123 63.326027

4 −0.876031 0.113975 63.317978

5 −0.876211 0.113981 63.317978

6 −0.876211 0.113981 63.317978

updated (Table 6.2), and converge quickly. The ﬁnal ﬁtted Poisson glm has

the systematic component

log ˆμ = −0.8762 + 0.1140x. (6.11)



Naturally, explicitly using the iterative procedure just described is not

necessary when using r. Instead, the function glm() is used, where the sys-

tematic component is speciﬁed in the same way as for normal linear regression

models (Sect. 2.6). Specifying the edm family distribution and the link func-

tion is also necessary. See Sect. 6.9 for more details about using r to ﬁt glms.

Example 6.3. Fit the Poisson glm suggested in Example 6.2 (data set:

nminer) as follows:

> library(GLMsData); data(nminer)

> nm.m1 <- glm( Minerab ~ Eucs, data=nminer,

family=poisson(link="log"),

control=list(trace=TRUE) ) # Shows the deviance each iteration

Deviance = 82.14668 Iterations - 1

Deviance = 64.49515 Iterations - 2

Deviance = 63.32603 Iterations - 3

Deviance = 63.31798 Iterations - 4

Deviance = 63.31798 Iterations - 5

248 6 Generalized Linear Models: Estimation

> nm.m1

Call: glm(formula = Minerab ~ Eucs, family = poisson(link = "log"),

data = nminer, control = list(trace = TRUE))

Coefficients:

(Intercept) Eucs

-0.8762 0.1140

Degrees of Freedom: 30 Total (i.e. Null); 29 Residual

Null Deviance: 150.5

Residual Deviance: 63.32 AIC: 121.5

The ﬁtted object nm.m1 contains a wealth of information about the ﬁtted

glm, which is discussed in the sections that follow. 

6.4 The Residual Deviance

The unit deviance (Sect. 5.4.1) captures the part of an edm probability func-

tion which depends on μ, as distinct from φ.Foraglm, the total deviance

(Sect. 5.7) captures that part of the log-likelihood function which depends on

the μ

. So, for the purpose of estimating the β

, maximizing the log-likelihood

is equivalent to minimizing the total deviance.

The total deviance can be computed at each stage of the irls algorithm

(Sect. 6.3) by comparing the responses y

with the ﬁtted values at each iter-

ation of the irls algorithm ˆμ

(r)

. r uses the total deviance to declare conver-

gence at iteration r when

|D(y, ˆμ

(r)

) − D(y, ˆμ

(r−1)

|D(y, ˆμ

(r)

)| +0.1

<,

where  =10

−8

is the default value.

After computing the mles

and corresponding ﬁtted values ˆμ,theresid-

ual deviance is the minimized total deviance

D(y, ˆμ)=



i=1

d(y

, ˆμ

). (6.12)

The residual deviance is a measure of the residual variability across n obser-

vations after ﬁtting the model, similar to the rss (2.8) for linear regression

models. In fact, as Example 6.4 shows, the residual deviance is precisely the

rss for normal linear regression models. The quantity D

∗

(y, ˆμ)=D(y, ˆμ)/φ

is called the scaled residual deviance. Computing the scaled residual deviance

obviously requires knowledge of the value of φ.

6.4 The Residual Deviance 249

Tabl e 6. 3 The unit deviance d(y

, ˆμ

) for each observation i and the residual deviance

D(y, ˆμ) for the noisy miner data, where w

=1foralli (Example 6.5)

y ˆμd(y, ˆμ) wd(y, ˆμ)

00.5230 1.0459 1.0459

01.3016 2.6032 2.6032

32.5792 0.0652 0.0652

24.0691 1.2971 1.2971

83.6307 3.9016 3.9016

Residual deviance: 63.3180

The residual deviance for a ﬁtted glm in r named fit is returned using

deviance(fit).

Example 6.4. Using the unit deviance from Example 5.1, the residual dev-

iance for the normal distribution is

D(y, ˆμ)=



i=1

− ˆμ

)

= rss,

and the scaled deviance is

∗

(y, ˆμ)=



i=1

− ˆμ

)



i=1



− ˆμ



provided the value of σ

is known. 

Example 6.5. Using the unit deviance for the Poisson distribution (Table 5.1,

p. 221), the residual deviance for the Poisson distribution is

D(y, ˆμ)=2



i=1



log

ˆμ

− (y

− ˆμ

)



Since φ = 1 for the Poisson distribution, the scaled residual deviance is identi-

cal to the residual deviance. Consider Model (6.11)(p.247) ﬁtted to the noisy

miner data in Example 6.2 (data set: nminer). Summing the unit deviances

(Table 6.3), the residual deviance for the model is D(y, ˆμ)=63.3180, where

ˆμ =exp(−0.8762 + 0.1140x)from(6.11). Using r, the residual deviance is

> deviance(nm.m1)

[1] 63.31798



250 6 Generalized Linear Models: Estimation

6.5 Standard Errors for

After computing the mles

, the standard errors for the estimates are com-

puted from the information matrix I

(β) shown in (6.8). The standard er-

rors are the square roots of the diagonal elements of the inverted information

matrix. Speciﬁcally,

se(



φv

(6.13)

where the v

are the square-root diagonal elements of the inverse of the

working information matrix with (j, k)th element



i=1

.Ifφ is not

known, then some estimate of it is used.

Example 6.6. Consider Model (6.11)(p.247) ﬁtted to the noisy miner data in

Example 6.2 (data set: nminer). The summary output for the glm in r shows

the mles for the two coeﬃcients, and the corresponding standard errors:

> coef(summary(nm.m1))

Estimate Std. Error z value Pr(>|z|)

(Intercept) -0.8762114 0.28279293 -3.098421 1.945551e-03

Eucs 0.1139813 0.01243104 9.169092 4.770189e-20



* 6.6 Estimation of β: Matrix Formulation

In matrix terms, the score vector U =[U

,...,U

]

for β is

U =

WM(y − μ), (6.14)

where W is the diagonal matrix of working weights W

(6.7) and M is the di-

agonal matrix of link derivatives dη

/dμ

. This gives the vector of derivatives

of the log-likelihood with respect to the coeﬃcient vector β =[β

,...,β

The Fisher information matrix for β, with elements I

(β)is

I =

WX. (6.15)

The Fisher scoring iteration (Sect. 4.8) to compute the mle of β is

(r+1)

(r)

+ I(

(r)

)

−1

(r)

) (6.16)

(r)

+(X

WX)

−1

WM(y −

μ), (6.17)

where the superscript (r) denotes the rth iterate, and all quantities on the

right hand side (including

μ) are evaluated at

(r)

. Note that φ cancels out

of the term I()

−1

U() on the right hand side.

6.6 Estimation of β: Matrix Formulation 251

The scoring iteration can be re-organized as iteratively weighted least

squares as

(r+1)

=(X

WX)

−1

Wz (6.18)

where z is the working response vector

z =

η +M(y −

μ), (6.19)

where all quantities on the right hand side are evaluated at

(r)

. After each

iteration, the linear predictor is updated as

(r+1)

= o +X

(r+1)

, where

o is the vector of oﬀsets, and the ﬁtted values are updated as

(r+1)

−1

(

(r+1)

After the iterations have converged, the covariance matrix of the regression

parameters is estimated from inverse information matrix

var[

β]=I

−1

= φ(X

WX)

−1

where some estimate of φ must be used if the value of φ is unknown. In

particular, the standard errors are obtained from the diagonal elements

se(



φv

where the v

are the square-root diagonal elements of (X

WX)

−1

Example 6.7. The covariance matrix of the coeﬃcients for the noisy miner

data (nminer) is in the output variable cov.scaled that is contained in the

model summary():

> nm.m1 <- glm( Minerab ~ Eucs, data=nminer, family=poisson)

> cov.mat <- summary(nm.m1)$cov.scaled

> round( cov.mat, digits=5)

(Intercept) Eucs

(Intercept) 0.07997 -0.00324

Eucs -0.00324 0.00015

The standard errors se(

) are the square root of the diagonal elements:

> sqrt( diag( cov.mat ) )

(Intercept) Eucs

0.28279293 0.01243104

These agree with the standard errors computed by r within computer preci-

sion (Example 6.6,p.250). 

The variance of

μ is found by ﬁrst considering

η. Consider given values of

the p



explanatory variables, given in the row vector x

. The best estimate

of η is ˆη = x

β. The variance of ˆη is

var[ ˆη]=var[x

β]=x

WX)

−1

φ,

252 6 Generalized Linear Models: Estimation

where some estimate of φ must be used if the value of φ is unknown. The

variance of ˆμ is harder to compute directly. However, for inference involving

μ (such as conﬁdence intervals for μ), we work with ˆη and then convert to ˆμ

via the link function μ = g

−1

(η).

6.7 Estimation of GLMs Is Locally Like Linear

Regression

The formulation of the scoring algorithm for maximum likelihood estimation

of glmsasirls (Sects. 6.3 and 6.6) is much more than a computational con-

venience. It reveals an analogy between glms and linear regression which

has many uses. To a ﬁrst approximation, ﬁtting a glm is equivalent to least

squares regression with responses z

and weights W

, with the working re-

sponses and working weights set to their ﬁnal converged values. Conveniently,

the working residuals

= z

− ˆη

(6.20)

and the working weights are stored as part of the standard output when glms

are ﬁtted in r (as fit$residuals and fit$weights respectively for a ﬁtted

model called fit). This means that all the methodology developed in Chaps. 2

and 3 can be applied to glms, simply by treating the working responses and

working weights as ﬁxed values. Quantities which may be computed in this

way include the ﬁtted values ˆμ; the variance of

; the leverages h; the value

of the raw residuals; Cook’s distance; dffits; dfbetas. These connections

are explored in later chapters.

6.8 Estimating φ

6.8.1 Introduction

Although knowledge of φ was not required for estimating the β

, it will be

required for hypothesis testing and conﬁdence intervals (Chap. 7). So, unless

φ is known a priori, it must be estimated. The most useful estimators of φ

are described in this section.

The most common models for which φ is known are binomial and Poisson

edms. Even then, estimation of φ can sometimes be useful when we wish to

relax the usual assumptions, as we will see in Sects. 9.8 and 10.5.

6.8 Estimating φ 253

6.8.2 The Maximum Likelihood Estimator of φ

In principle, we could apply mle directly to the log-likelihood to estimate φ,

just as we did for the β

. However the mle of φ is seriously biased, unless n

is very large relative to p



Consider the case of normal linear regression models. Then the mle of

φ = σ

ˆσ



i=1

− ˆμ

)

, (6.21)

which is never used because it is biased. Instead,

n − p





i=1

− ˆμ

)

, (6.22)

is unbiased and is used in practice.

There are at least three ways to generalize the unbiased estimator s

glms so that the normal linear regression model results remain special cases

of the glm results. We consider these in the next three subsections.

6.8.3 Modiﬁed Proﬁle Log-Likelihood Estimator of φ

A more sophisticated strategy for estimating φ is based on the proﬁle log-

likelihood. The proﬁle log-likelihood estimate for φ is found by ﬁrst assuming

φ is ﬁxed and maximizing the log-likelihood with respect to β. Write the log-

likelihood as (

,...,

,φ; y). Then, write the log-likelihood as a function

of φ, treating each

as being ﬁxed and maximize this log-likelihood with re-

spect to φ. That is, the proﬁle log-likelihood for φ is (φ)=(

,...,

,φ; y).

The modiﬁed proﬁle log-likelihood (mpl) is, as the name suggests, a mod-

iﬁcation of the proﬁle log-likelihood with better properties:



(φ)=



log φ + (

,...,

,φ; y).

The modiﬁed proﬁle log-likelihood includes a penalty term which penalizes

small values of φ. The value of φ maximizing 

(φ) is called the modiﬁed

proﬁle log-likelihood estimator of φ, and is denoted

.Thempl estimator

is a consistent estimator and is approximately unbiased, even in quite small

samples.

The main disadvantage of the mpl estimator is that, like the mle,itis

often inconvenient to compute. The estimator generally requires iterative

estimation (as usual, the normal linear case is an exception). Even more

254 6 Generalized Linear Models: Estimation

seriously, the derivatives of the log-likelihood with respect to φ involve the

terms ∂a(y, φ/w)/∂φ, which for some edms are diﬃcult to obtain since a()

may not have a closed form.

Example 6.8. Consider the normal distribution. The proﬁle log-likelihood is

(σ

)=−



i=1

log 2πσ

−

2σ



i=1

− ˆμ

)

Diﬀerentiating with respect to σ

, setting to zero, and solving for σ

produces

the proﬁle log-likelihood estimate (identical to the mle (6.21) for this case).

The modiﬁed proﬁle log-likelihood is



(σ



log σ

−



i=1

log 2πσ

−

2σ



i=1

− ˆμ

)

Diﬀerentiating with respect to σ

, setting to zero, and then solving, produces

the modiﬁed proﬁle likelihood estimator of σ

(ˆσ

)

n − p





i=1

− ˆμ

)

identical to s

in (6.22). 

6.8.4 Mean Deviance Estimator of φ

It is easy to show (Problem 6.4) that, if the saddlepoint approximation for the

edm probability function (5.4.4) is exact, the maximum likelihood estimator

of φ is the simple mean deviance D(y, ˆμ)/n. Like all mles, this estimator fails

to take account of estimation of the β

and the residual degrees of freedom.

The linear regression case (6.22) motivates the mean deviance estimator of φ:

φ =

D(y, ˆμ)

n − p



Example 6.9. For normal glms, the residual deviance is equal to the rss,so

the mean deviance estimator of the dispersion parameter is simply

φ = s

the usual unbiased estimator of σ

(6.22). 

6.8 Estimating φ 255

6.8.5 Pearson Estimator of φ

As pointed out in Sect. 6.7, glms can be treated to a ﬁrst approximation like

least squares models. Suppose we take this approach, and compute the rss

from the ﬁtted model, treating the working responses and working weights

as the actual responses and weights. This gives the working rss



i=1

− ˆη

)

(6.23)



i=1

− ˆμ

)

V (ˆμ

)

, (6.24)

known as the Pearson statistic. Note that the unit Pearson statistic {w(y −

ˆμ)

}/V (ˆμ) represents the contribution to the Pearson statistic of each obser-

vation, just as the unit deviance does for the deviance. The Pearson statistic

makes intuitive sense as a measure of residual variability because the variance

function V (ˆμ) in the denominator of the unit statistic divides out the eﬀect

of non-constant variance from the squared residuals.

Continuing the analogy with least squares, the Pearson estimator of φ is

deﬁned by

φ =

n − p



. (6.25)

Example 6.10. For normal glms, V (μ) = 1 (Table 5.1,p.221) so the Pearson

statistic reduces to the usual rss, X

= rss, and the Pearson estimator of

the dispersion parameter is

φ = s

. The normal is the only distribution for

which the the mean deviance and Pearson estimators of φ are the same. 

Example 6.11. The Poisson distribution has the variance function V (μ)=μ

(Table 5.1,p.221), so the Pearson statistic is



i=1

− ˆμ

)

ˆμ



6.8.6 Which Estimator of φ Is Best?

Given the diﬀerent methods for estimating φ, which should be used? The

mle

φ is biased, unless p



/n is very small, so

φ is rarely used. On the other

hand, the modiﬁed proﬁle estimator

has excellent theoretical properties.

It should be nearly eﬃcient and nearly consistent. However it is often incon-

venient to compute.

256 6 Generalized Linear Models: Estimation

The mean deviance and Pearson estimators are very convenient, as they

are readily available from the unit deviances and working residuals respec-

tively. The mean deviance estimator should behave well when the saddlepoint

approximation holds; that is, for normal or inverse Gaussian glms or when

φ is relatively small. The Pearson estimator, however, is almost universally

applicable, because (y − μ)

/V (μ) should always be unbiased for φ if μ is

the correct mean and V (μ) is the correct variance function. In other words,

the Pearson estimator is approximately unbiased given only ﬁrst and second

moment assumptions. This makes the Pearson estimator the most robust es-

timator, in the sense that it relies on fewest assumptions. For this reason, the

glm() function in r uses the Pearson estimator for φ by default. In practice,

the Pearson estimator tends to be more variable (less precise) but less biased

than the mean deviance estimator.

As usual, it makes no diﬀerence for normal glms, because

φ and

φ are

identical, and equal to the residual variance s

used in Chaps. 2 and 3.

For gamma glms, the mean deviance estimator can be sensitive to round-

ing errors as y approaches zero [5, p. 295, 296]. Indeed, the plot of the unit

deviance (Fig. 5.2, bottom left panel, p. 222) shows how the value of d(y,μ)

increases rapidly as y → 0. A small change in y when y is small can result in

a correspondingly large change in the value of d(y, μ) and hence in the value

of D(y, ˆμ). For this reason, the Pearson estimator may be preferred to the

mean deviance estimator for gamma glms when rounding is an issue; that

is, when small responses are not recorded to at least two or three signiﬁcant

ﬁgures. The same remark applies to other edms with support on the positive

real line.

For binomial and Poisson glms, φ = 1 and no estimation is necessary.

However, the issue may arise for over-dispersed binomial or Poisson glms,

which are considered in later chapters.

Example 6.12. In Example 3.14 (data set: trees), a gamma glm is suggested

for the cherry tree data, with systematic component log μ = β

+ β

log d +

log h. To ﬁt this model in r,use:

> data(trees)

> cherry.m1 <- glm( Volume ~ log(Height) + log(Girth), data=trees,

family=Gamma(link="log"))

The regression parameters are

> coef( cherry.m1 )

(Intercept) log(Height) log(Girth)

-6.691109 1.132878 1.980412

Compute the Pearson estimator of φ deﬁned by (6.23) explicitly in r using:

> w <- weights(cherry.m1, type="working")

> e <- residuals(cherry.m1, type="working")

> sum( w * e^2 ) / df.residual(cherry.m1);

[1] 0.006427286

6.9 Using R to Fit GLMs 257

Alternatively, since the Pearson estimator is used by default in r:

> summary(cherry.m1)$dispersion

[1] 0.006427286

The mean deviance estimator is

> deviance(cherry.m1) / df.residual(cherry.m1)

[1] 0.006554117

The two estimates are similar. 

6.9 Using R to Fit GLMs

In r, glms are ﬁtted to data using the function glm(), and the inputs

formula, data, weights and subset are used in the same way as for lm()

(see Sect. 2.14,p.79). The systematic component is given by the formula in-

put, speciﬁed in the same way as for linear regression models using lm().To

use glm(), the distribution and link function also must be speciﬁed using the

input family. As an example, a glm(Poisson; log) model is speciﬁed using

glm(y~x1+x2,family=poisson(link="log") )

Similarly, a glm(binomial; logit) model is speciﬁed as

glm(y~x1+x2,family=binomial(link="logit") )

If a link function is not explicitly given, the default link function used by r

is the canonical link function (Table 6.4). As an example, the models above

could be speciﬁed as

glm(y~x1+x2,family=poisson )

glm(y~x1+x2,family=binomial )

since the logarithmic link function is the canonical link function for a Poisson

glm, and the logistic link function is the canonical link function for the

binomial glm.

In r, valid glm families are (noting the capitalization carefully):

• gaussian(): Specifying the Gaussian (normal) distribution;

• binomial(): Specifying a binomial edm (Chap. 9);

• poisson(): Specifying a Poisson edm (Chap. 10);

• Gamma(): Specifying a gamma edm (Chap. 11);

• inverse.gaussian(): Specifying an inverse Gaussian edm (Chap. 11).

More details are provided about each family in the indicated chapters. Three

other families are discussed in Sect. 8.10, and are mentioned here for complete-

ness: quasi(), quasibinomial() and quasipoisson(). Other families can

also be used by writing a new family function. For example, the tweedie()

family function (in package statmod) was written to enable the ﬁtting of

258 6 Generalized Linear Models: Estimation

Tabl e 6 .4 The link functions accepted by diﬀerent glm() families in r are indicated

using a tick . The default (and canonical) links used by r are indicated with stars 

(Sect. 6.9)

Link binomial and poisson and

function gaussian quasibinomial quasipoisson Gamma inverse.gaussian quasi

identity 

log  

inverse 

sqrt 

1/mu^2 

logit 

probit 

cauchit 

cloglog 

power 

Tweedie glms (Chap. 12). The diﬀerent families accept diﬀerent link func-

tions, and have diﬀerent defaults (Table 6.4). The quasi() family also ac-

cepts link functions deﬁned using power(), which have the form η = μ

for

λ ≥ 0; the logarithmic link function is obtained when λ =0.

Usually, the output from a ﬁtted glm is sent to an output object: fit <-

glm(y ~ x1 + x2, family=poisson), for example. The output object fit

contains substantial information; see ?glm. The most useful information is

extracted from fit using extractor functions, which include:

• coef(fit): Returns the coeﬃcients

of the systematic component.

• deviance(fit): Returns the residual deviance D(y, ˆμ) for the ﬁtted glm.

• summary(fit): Returns the summary of the ﬁtted glm (some parts of

which are discussed in Chap. 7), with the corresponding standard er-

rors, t-orz-statistics and two-tailed P -values for testing H

: β

=0;

the value of φ, or the Pearson estimate of φ if φ is unknown; the

residual deviance D(y, ˆμ) and corresponding residual degrees of free-

dom; and the aic. The output of summary() (for example, out <-

summary(fit)) contains substantial information (see ?summary.glm).

For example, out$dispersion displays the value of φ or its estimate,

whichever is appropriate; coef(out) displays the parameter estimates

and standard errors, plus the t-orz-values and two-tailed P -values for

testing H

: β

=0.

• df.residual(fit): Extracts the residual degrees of freedom.

• fitted(fit): Extracts the ﬁtted values ˆμ; fitted.values(fit) is

equivalent.

The algorithm for ﬁtting glmsinr is usually stable and fast. However,

sometimes the parameters controlling the ﬁtting algorithm need to be ad-

justed using the input glm.control() when calling the glm() function. The

following parameters can be adjusted:

6.10 Summary 259

• The convergence criterion (Sect. 6.4,p.248), where epsilon is the value

of . By default, epsilon =10

−8

. Setting epsilon to some other (usually

smaller) value is occasionally useful.

• The maximum number of iterations, by changing the value of maxit.

By default, the irls algorithm is permitted a maximum of 25 iterations.

Occasionally the value of maxit needs to be increased to ensure the Fisher

scoring algorithm converges.

• The information displayed. If the algorithm fails or produces unexpected

results, viewing the details of each iteration in the irls algorithm can

help diagnose the problem, by setting trace=TRUE.

As with lm(), models may be updated using update() rather than being

completely speciﬁed (see Sect. 2.10.1,p.61).

Example 6.13. The noisy miner data (data set: nminer) has been used in

examples in this chapter. The following r commands ﬁt Model (6.11)(p.247):

> data(nminer)

> nm.m1 <- glm( Minerab ~ Eucs, data=nminer, family=poisson)

The r summary() for this model is shown in Fig. 6.1.

To demonstrate the use of glm.control(), we ﬁt the model by changing

the ﬁtting parameters. We set the convergence criterion to  =10

−15

, permit

a maximum of three iterations, and view the details of each iteration:

nm.m2 <- update( nm.m1, control=glm.control(

maxit=3, # Max of 3 iterations

epsilon=1e-15, # Stopping criterion

trace=TRUE) ) # Show details

Deviance = 82.14668 Iterations - 1

Deviance = 64.49515 Iterations - 2

Deviance = 63.32603 Iterations - 3

Warning message:

In glm.fit(x = X,y=Y,weights = weights, start = start,

etastart = etastart, : algorithm did not converge

The algorithm has not converged in three iterations to the requested level

of accuracy  =10

−15

:thetrace shows that the residual deviance is yet to

converge. 

6.10 Summary

Chapter 6 discusses ﬁtting glms to data. Fitting glms relies on the structure

provided by edms. For example, for edms (Sect. 6.2) the derivative

∂ log P(y; μ, φ/w)

∂μ

w(y − μ)

φV (μ)

260 6 Generalized Linear Models: Estimation

Fig. 6.1 An example of the output of the summary() command after using glm()

(Sect. 6.9)

has a simple form. The estimates

are found by Fisher scoring, using the

iteratively reweighted least squares (irls) algorithm (Sect. 6.3). Importantly,

the value of φ is not needed to ﬁnd estimates of the β

The matrix form of the score equations and the information matrix for

β are U =X

WM(y − μ)/φ and I =X

WX/φ, where W is the diagonal

matrix of working weights W

, and M is the diagonal matrix of link derivatives

dη

/dμ

(Sect. 6.6).

The residual deviance D(y, ˆμ)=



i=1

d(y

, ˆμ

) is a measure of the total

residual variability from a ﬁtted model across n observations (Sect. 6.4). The

scaled residual deviance is D

∗

(y, ˆμ)=D(y, ˆμ)/φ (Sect. 6.4).

The standard errors of

are se(

√

φv

, where the v

are the square-

root diagonal elements of the inverse of the working information matrix. If φ

is not known, then some estimate of it is used (Sect. 6.5).

Importantly, the estimation algorithm for ﬁtting glms is locally the same

as for ﬁtting linear regression models, so various quantities used in regression

can be computed from the ﬁnal iteration of the irls algorithm for glms,

such as the ﬁtted values, the variance of

, leverages, Cook’s distance values,

dffits, dfbetas and the raw residuals (Sect. 6.7).

6.10 Summary 261

The dispersion parameter can be estimated using a modiﬁed proﬁle

log-likelihood estimator

(Sect. 6.8.3), the mean deviance estimator

(Sect. 6.8.4) or the Pearson estimator

φ (Sect. 6.8.5). For all these estima-

tors, the linear regression model results are special cases of the glm results

(Sect. 6.8). In r, the dispersion parameter φ is estimated using the Pearson

estimate (Sect. 6.8).

The next chapter considers methods for inference concerning the ﬁtted

model.

Problems

Selected solutions begin on p. 537. Problems preceded by an asterisk * refer

to the optional sections in the text, and may require matrix manipulations.

6.1. Consider a link function η = g(μ). Find the ﬁrst two terms of the Tay-

lor series expansion of g(y) expanded about μ, and show that the result is

equivalent to z, the working responses (6.9)(p.246).

*6.2.Consider the linear regression model. Show that the iteration (6.18)

(p. 251) reduces to the equation for ﬁnding the regression parameter estimates

in the linear regression model case:

β =(X

WX)

−1

Wy.

6.3. If μ is known, show that the Pearson estimator of φ is unbiased (that is,

φ]=φ).

6.4. Suppose the saddlepoint approximation (Sect. 5.4.2)

P(y; μ, φ)isused

to approximate the edm probability function P(y; μ, φ). After writing

(μ, φ; y)=



i=1

log

P(y

; μ

,φ), show that the solution to ∂

(μ, φ; y)/∂φ =0

is the simple mean deviance D(y, ˆμ)/n.

6.5. If the canonical link function is used in a glm, then V (μ)=1/g



(μ)=

dμ/dη (Problem 5.20). Assuming a canonical link function, show that:

1. U (β



i=1

− μ

/φ.

2. dU (β

)/dμ = −



i=1

/φ.

These results are used in some of the problems that follow.

6.6. Consider a binomial glm using the canonical link function.

1. Determine the score function U (β

) and the Fisher information I

(β).

2. Determine the working responses z

Hint: The results from Problem 6.5 will prove useful.

6.7. Consider a gamma glm using the canonical link function.

1. Determine the score function U (β

) and the Fisher information I

(β).

2. Determine the working responses z

3. Determine the Pearson estimator of φ.

Hint: The results from Problem 6.5 will prove useful.

262 REFERENCES

6.8. Repeat Problem 6.7, but using the often-used logarithmic link function

instead of the canonical link function.

6.9. Consider an inverse Gaussian glm using a logarithmic link function,

which is not the canonical link function.

1. Determine the score function U (β

) and the Fisher information I

(β).

2. Determine the working responses z

3. Find the mle of φ.

4. Find the mean deviance estimator of φ.

5. Find the Pearson estimator of φ.

6.10. Children were asked to build towers as high as they could out of cubical

and cylindrical blocks [3, 6]. The number of blocks used and the time taken

were recorded (data set: blocks). In this problem, only consider the number

of blocks used y and the age of the child x. In Problem 5.25,aglm was

proposed for these data.

1. Fit this glm using r, and write down the ﬁtted model.

2. Determine the standard error for each regression parameter.

3. Compute the residual deviance.

6.11. Nambe Mills, Santa Fe, New Mexico [2, 7], is a tableware manufacturer.

After casting, items produced by Nambe Mills are shaped, ground, buﬀed, and

polished. In 1989, as an aid to rationalizing production of its 100 products, the

company recorded the total grinding and polishing times and the diameter of

each item (Table 5.3; data set: nambeware). In this problem, only consider the

item price y and the item diameter x. In Problem 5.26,aglm was proposed

for these data.

1. Fit this glm using r, and write down the ﬁtted model.

2. Determine the standard error for each regression parameter.

3. Compute the residual deviance.

4. Compute the mean deviance estimate of φ.

5. Compute the Pearson estimate of φ.

References

[1] Chatﬁeld, C.: Problem Solving: A Statistician’s Guide, second edn. Texts

in Statistical Science. Chapman and Hall/CRC, London (1995)

[2] Data Desk: Data and story library (dasl) (2017). URL http://dasl.

datadesk.com

[3] Johnson, B., Courtney, D.M.: Tower building. Child Development 2(2),

161–162 (1931)

[4] Maron, M.: Threshold eﬀect of eucalypt density on an aggressive avian

competitor. Biological Conservation 136, 100–107 (2007)

REFERENCES 263

[5] McCullagh, P., Nelder, J.A.: Generalized Linear Models, second edn.

Monographs on Statistics and Applied Probability. Chapman and Hall,

London (1989)

[6] Singer, J.D., Willett, J.B.: Improving the teaching of applied statistics:

Putting the data back into data analysis. The American Statistician

44(3), 223–230 (1990)

[7] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

Chapter 7

Generalized Linear Models:

Inference

There is no more pressing need in connection with the

examination of experimental results than to test whether

a given body of data is or is not in agreement with any

suggested hypothesis.

Sir Ronald A. Fisher [2, p. 250]

7.1 Introduction and Overview

Section 4.10 discussed three types of inferential approaches based on likeli-

hood theory: Wald, score and likelihood ratio. In Chap. 7, these approaches

are applied in the context of glms. We ﬁrst consider inference when φ is

known (Sect. 7.2), then the large-sample asymptotic results (Sect. 7.3) that

underlie all the distributional results for the test statistics in that section.

Section 7.4 then introduces goodness-of-ﬁt tests to determine whether the

linear predictor suﬃciently describes the systematic trends in the data. The

distributional results for these goodness-of-ﬁt tests rely on small dispersion

asymptotic results (the large sample asymptotics do not apply), which are

discussed in Sect. 7.5 where guidelines are presented for when these results

hold. We then consider inference when φ is unknown (Sect. 7.6), and include a

discussion of using the diﬀerent estimates of φ. Wald, score and likelihood ra-

tio tests are then compared (Sect. 7.7). Techniques for comparing non-nested

glms (Sect. 7.8) are then discussed, followed by automated methods for se-

lecting glms (Sect. 7.9).

7.2 Inference for Coeﬃcients When φ Is Known

7.2.1 Wald Tests for Single Regression Coeﬃcients

The simplest tests concerning regression coeﬃcients are Wald tests, because

they depend only on the estimated coeﬃcients and standard errors. The re-

gression coeﬃcients

are approximately normally distributed when n is

reasonably large, and this is the basis of Wald tests.

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_7

265

266 7 Generalized Linear Models: Inference

Consider a glm with p



regression parameters ﬁtted to some data in a

situation where φ is known. The Wald test of the null hypothesis H

: β

= β

where β

is some given value (typically zero), consists of comparing

− β

to the standard error of

(Sect. 4.10.1). For a glm with φ known, the Wald

test statistic is

Z =

− β

se(

)

where the standard error se(

√

φv

is given by (6.13). If H

is true, Z

follows approximately the standard normal distribution.

In r, using the summary() command shows the values of Z,se(

) and the

two-tailed P-values for testing β

= 0 for each ﬁtted regression parameter.

Example 7.1. For the noisy miner data [4] (Example 1.5; data set: nminer),

the Wald statistics for testing H

: β

= 0 for each parameter in the ﬁtted

model are shown as part of the output of the summary() command. More

brieﬂy, coef(summary()) shows just the information about the coeﬃcients:

> library(GLMsData); data(nminer)

> nm.m1 <- glm( Minerab ~ Eucs, data=nminer, family=poisson)

> printCoefmat( coef( summary(nm.m1) ) )

Estimate Std. Error z value Pr(>|z|)

(Intercept) -0.876211 0.282793 -3.0984 0.001946 **

Eucs 0.113981 0.012431 9.1691 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The evidence suggests both coeﬃcients in the model are non-zero. 

7.2.2 Conﬁdence Intervals for Individual Coeﬃcients

Conﬁdence intervals may be computed using the Wald, score, or the

likelihood-ratio test statistic as in Sect. 4.11 (p. 200). In practice, the Wald

statistic is most commonly used, because the necessary quantities for com-

puting the Wald standard errors are computed in the ﬁnal iteration of the

ﬁtting algorithm so no further computations are necessary. Conﬁdence inter-

vals based on Wald statistics are symmetric on the η scale. The 100(1 −α)%

conﬁdence interval for β

when φ is known is

± z

∗

α/2

se(

)

where z

∗

α/2

is the value of z such that an area α/2 is in each tail of the standard

normal distribution. The r function confint() computes Wald conﬁdence

intervals from ﬁtted glm() objects.

7.2 Inference for Coeﬃcients When φ Is Known 267

Example 7.2. For the noisy miner data (data set: nminer), the 95% conﬁdence

intervals for both coeﬃcients are:

> confint(nm.m1)

2.5 % 97.5 %

(Intercept) -1.45700887 -0.3465538

Eucs 0.08985068 0.1386685



7.2.3 Conﬁdence Intervals for μ

The ﬁtted values ˆμ estimate the mean value for given values of the explana-

tory variables. Since ˆη = g(ˆμ) is estimated from the

, which are estimated

with uncertainty, the estimates of ˆμ are also estimated with uncertainty. We

initially work with ˆη, for which var[ ˆη] is easily found (Sect. 6.6). When φ is

known, a 100(1 − α)% Wald conﬁdence interval for η is

ˆη ± z

∗

α/2

se(ˆη),

where se(ˆη)=



var[ ˆη], and where z

∗

α/2

is the value such that an area α/2is

in each tail of the standard normal distribution. The conﬁdence interval for

μ is found by applying the inverse link function (that is, μ = g

−1

(η)) to the

lower and upper limit of the interval found for ˆη. Note that the conﬁdence

interval is necessarily symmetric on the η scale.

Rather than explicitly returning a conﬁdence interval, r optionally returns

the standard errors when making predictions using predict(), by using the

input se.fit=TRUE. This information can be used to form conﬁdence inter-

vals. Note that predict() returns the value of ˆη by default, and the ﬁtted

values ˆμ (and corresponding standard errors if se.fit=TRUE) are returned

by specifying type="response".

Example 7.3. For the noisy miner data nminer, suppose we wish to estimate

the mean number of noisy miners for a transect with ten eucalyptus trees per

2 ha transect. First, we compute the predictions and standard errors on the

scale of the linear predictor:

> # By default, this computes statistics on the linear predictor scale:

> out <- predict( nm.m1, # The model used to predict

newdata=data.frame(Eucs=10), # New data for predicting

se.fit=TRUE) # Return the std errors

> out2 <- predict( nm.m1, newdata=data.frame(Eucs=10), se.fit=TRUE,

type="response") # Return predictions on mu scale

> c( exp( out$fit ), out2$fit ) # Both methods give the same answer

1.30161 1.30161

268 7 Generalized Linear Models: Inference

l l

llll l ll l

0 5 10 15 20 25 30 35

No. eucalypts per 2 ha transect

No. noisy miners

Fig. 7.1 The predicted relationship between the mean number of noisy miners and the

number of eucalyptus trees (solid), with the 95% conﬁdence intervals shown (dashed

lines) (Example 7.3)

Then we form the conﬁdence interval for μ by using the inverse of the loga-

rithmic link function:

> zstar <- qnorm(p=0.975) # For 95% CI

> ci.lo <- exp( out$fit - zstar*out$se.fit)

> ci.hi <- exp( out$fit + zstar*out$se.fit)

> c( Lower=ci.lo, Estimate=exp(out$fit), Upper=ci.hi)

Lower.1 Estimate.1 Upper.1

0.924013 1.301610 1.833512

We see that ˆμ =1.302, and that the 95% interval is from 0.9240 to 1.834.

Notice that this conﬁdence interval is not symmetric:

> c( ci.lo-exp(out$fit), ci.hi-exp(out$fit))

-0.3775972 0.5319019

This idea can be extended to show the conﬁdence intervals for all transects

with varying numbers of eucalyptus trees (Fig. 7.1):

> newEucs <- seq(0, 35, length=100)

> newMab <- predict( nm.m1, se.fit=TRUE, newdata=data.frame(Eucs=newEucs))

> ci.lo <- exp(newMab$fit-zstar*newMab$se.fit)

> ci.hi <- exp(newMab$fit+zstar*newMab$se.fit)

> plot( Minerab~Eucs, data=nminer,

xlim=c(0, 35), ylim=c(0, 20), las=1, pch=19,

xlab="No. eucalypts per 2 ha transect", ylab="No. noisy miners")

> lines(exp(newMab$fit) ~ newEucs, lwd=2)

> lines(ci.lo ~ newEucs, lty=2); lines(ci.hi ~ newEucs, lty=2)

The intervals are wider as ˆμ gets larger, since V (μ)=μ for the Poisson

distribution. 

7.2 Inference for Coeﬃcients When φ Is Known 269

7.2.4 Likelihood Ratio Tests to Compare Nested

Models: χ

Tests

Consider comparing two nested glms, based on the same edm but with dif-

ferent ﬁtted systematic components:

Model A: g(ˆμ

+ ···+

Model B: g(ˆμ

+ ···+

Notice that Model A is a special case of Model B, with p

.Wesay

that Model A is nested in Model B. To determine if the simpler Model A is

adequate for modelling the data, the hypothesis H

: β

= ···= β

is to be tested.

Under H

(that is, Model A is suﬃcient for the data), denote the ﬁt-

ted values as ˆμ

, producing the log-likelihood 

= 

(ˆμ

,...,ˆμ

,φ; y)and

residual deviance D(y, ˆμ

). For Model B, denoted the ﬁtted values as ˆμ

producing the log-likelihood 

= 

(ˆμ

,...,ˆμ

,φ; y) and residual deviance

of D(y, ˆμ

We have previously observed that the total deviance function captures

that part of the log-likelihood which depends on μ

. So, if φ is known, the

likelihood ratio test statistic for comparing Models A and B is

L =2{

− 

} =

D(y, ˆμ

) − D(y, ˆμ

)

. (7.1)

The dispersion model form of the edm (5.13) has been used here, and the

terms b(y, φ/w

) not involving μ

cancel out. Standard asymptotic likelihood

theory asserts that L ∼ χ



−p



approximately under the null hypothesis if

n is large relative to p



Likelihood ratio tests are traditionally used to test two-tailed alternative

hypotheses. However, if Model B and Model A diﬀer by only one coeﬃcient,

then we can deﬁne a signed likelihood ratio statistic to test a one-tailed

alternative hypothesis about the true coeﬃcient. Suppose that p



− p



=1.

We can deﬁne a z-statistic from the signed square-root of L as

Z = sign(

1/2

Standard asymptotic likelihood theory asserts that Z ∼ N(0, 1) under the

null hypothesis H

: β

= 0. The signed likelihood ratio test statistic can be

used similarly to Wald test statistics.

Example 7.4. For the noisy miner data nminer, we can ﬁt the model with

just a constant term in the model, then the model with both a constant term

and the number of eucalypts in the model:

> nm.m0 <- glm( Minerab ~ 1, data=nminer, family=poisson)

> nm.m1 <- glm( Minerab ~ Eucs, data=nminer, family=poisson)

270 7 Generalized Linear Models: Inference

Then compute the residual deviance and residual degrees of freedom for each

model:

> c( "Dev(m0)"= deviance( nm.m0 ), "Dev(m1)" = deviance( nm.m1 ) )

Dev(m0) Dev(m1)

150.54532 63.31798

> c( "df(m0)" = df.residual( nm.m0 ), "df(m1)" = df.residual( nm.m1 ) )

df(m0) df(m1)

30 29

Since φ = 1 for the Poisson distribution, use (7.1) to compare the two models:

> L <- deviance( nm.m0 ) - deviance( nm.m1 ); L

[1] 87.22735

> pchisq(L, df.residual(nm.m0) - df.residual(nm.m1), lower.tail=FALSE )

[1] 9.673697e-21

The P -value is very small, indicating that the addition of Eucs is signiﬁcant.



7.2.5 Analysis of Deviance Tables to Compare Nested

Models

Often a series of nested models is compared. The initial model might contain

no explanatory variables, then each explanatory variable might be added in

turn. If successive pairs of models are compared using likelihood ratio tests,

this amounts to computing diﬀerences in residual deviances for successive

models. The computations can be organized into an analysis of deviance

table (Table 7.1), which is a direct generalization of anova tables for linear

models (Sect. 2.10).

In r, the analysis of deviance table is produced using the anova() function.

The argument test="Chisq" must be speciﬁed to obtain P -values for the

deviances relative to χ

distributions on the appropriate degrees of freedom.

If φ is not equal to the default value of one, the value of φ can be provided

using the dispersion argument in the anova() call.

Example 7.5. For the noisy miner data nminer, and the models ﬁtted in

Example 7.4, produce the analysis of deviance table in r using:

Tabl e 7. 1 The analysis of deviance table for model nm.m1 ﬁtted to the noisy miner

data (Sect. 7.2.5)

Source Deviance df LP-value

Due to Eucs 87.23 1 87.23 < 0.001

Residual 63.32 29

Total 150.530

7.2 Inference for Coeﬃcients When φ Is Known 271

> anova(nm.m1, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 30 150.545

Eucs 1 87.227 29 63.318 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The residual deviances, and the diﬀerence between them, are the same as

reported in Example 7.4. Notice that r also reports the residual deviance

and residual degrees of freedom for each model in addition to the analysis of

deviance information. 

7.2.6 Score Tests

Score tests may also be used to test hypotheses about single parameters or

about sets of parameters. Whereas Wald and likelihood ratio tests are used to

test hypotheses about explanatory variables in the current ﬁtted model, score

tests enable testing of hypotheses about explanatory variables not (yet) in

the current model, but which might be added. Score tests play a strong role

in glm theory and practice because of their relationship to Pearson statistics.

Suppose we want to add a new predictor x

p+1

to an existing glm. Write

e(y)

for the ith working residual (6.20)fromtheglm. Similarly write

e(x

p+1

)

for the ith residual from the least squares regression of x

p+1

the existing predictors with weights W

. The score statistic for testing the

null hypothesis H

: β

p+1

=0is

Z =



i=1

e(x

p+1

)

e(y)

{



i=1

e(x

p+1

)

}

1/2

If H

is true, then Z ∼ N(0, 1) approximately. In r, score test statistics for

individual predictors are computed using the function glm.scoretest() in

package statmod.

Example 7.6. For the noisy miner data nminer, we conduct a score test to

determine if Eucs should be added to the null model using glm.scoretest():

> library(statmod) # Provides glm.scoretest

> nm.m0 <- glm( Minerab ~ 1, data=nminer, family=poisson)

> z.stat <- glm.scoretest(nm.m0, nminer$Eucs)

> p.val <- 2 * pnorm( abs(z.stat), lower.tail=FALSE)

> round( c(score.stat=z.stat, P=p.val), 4)

score.stat P

9.7565 0.0000

The evidence strongly suggests that Eucs should be added to the model. 

272 7 Generalized Linear Models: Inference

Example 7.7. The well-known Pearson chi-square test of independence in a

contingency table is an example of a score test. To illustrate this, we can

construct a small example:

> Y <- matrix(c(10,20,20,10),2,2)

> rownames(Y) <- c("A1","A2")

> colnames(Y) <- c("B1","B2")

B1 B2

A1 10 20

A2 20 10

The Pearson test P -value is:

> chisq.test(Y, correct=FALSE)$p.value

[1] 0.009823275

The same P -value can be obtained from a Poisson log-linear regression and

a score test for interaction:

> y <- as.vector(Y)

> A <- factor(c(1,2,1,2))

> B <- factor(c(1,1,2,2))

> fit <- glm(y~A+B, family=poisson)

> z.stat <- glm.scoretest(fit, x2=c(0,0,0,1))

> 2 * pnorm( -abs(z.stat) )

[1] 0.009823231



* 7.2.7 Score Tests Using Matrices

Suppose we wish to consider adding a set of k new explanatory variables to the

current glm. Write X

for the matrix with the new explanatory variables as

columns, and write E

for the matrix of residuals after least squares regression

of the columns of X

on the predictors already in the glm;thatis,

− X

)

−1

where X is the model matrix and W is the diagonal matrix of working weights

from the current ﬁtted model. Although this might seem an elaborate expres-

sion, E

can be computed very quickly and easily using the information stored

in the glm() ﬁt object in r.IfX

is a single column, then the Z score test

statistic is

Z =

)

1/2

7.3 Large Sample Asymptotics 273

where e is the vector of working residuals from the current ﬁtted model. If

is a matrix, then the chi-square score test statistic is

= e

)

−1

We.

Under the null hypothesis, that none of the new covariates are useful ex-

planatory variables, X

∼ χ

approximately.

In r, score test statistics for a set of predictors are computed using the

function glm.scoretest() in package statmod.

7.3 Large Sample Asymptotics

All the distributional results for the test statistics given in this chapter so far

are standard asymptotic results from likelihood theory (Sect. 4.10). The dis-

tributions should be good approximations when the number of observations

n is reasonably large. We call these results large sample asymptotics.

It is hard to give a guideline for how large n needs to be before we should

be conﬁdent that the asymptotics hold, but, on the whole, the results tend

to hold well for score tests and likelihood ratio tests even for moderate sized

samples. Wald tests, especially for binomial edms with small m, tend to need

larger samples to be reliable. For Wald tests, the asymptotic results tend to

be conservative, in that small samples generally result in large standard errors

and non-signiﬁcant Wald test statistics. When the sample size is large enough

for the standard errors se(

) to be small, then the asymptotics should be

reasonably accurate.

As usual, everything is exact for normal linear glms.

Example 7.8. Consider a small regression with binary data:

> y <- c(0, 0, 0, 1, 0, 1, 1, 1, 1)

>x<-1:9

> fit <- glm(y~x, family=binomial)

An exact permutation P -value can be obtained for this data using a Mann-

Whitney (or Wilcoxon) rank-sum test, without using any asymptotic assump-

tions. This shows there is good evidence for a trend in the data:

> wilcox.test(x ~ y)$p.value

[1] 0.03174603

The Wald z-test proves to be conservative, failing to detect the trend:

> coef(summary(fit))

Estimate Std. Error z value Pr(>|z|)

(Intercept) -5.811289 4.0019503 -1.452114 0.1464699

x 1.292257 0.8497008 1.520838 0.1283006

274 7 Generalized Linear Models: Inference

The likelihood ratio test possibly over-states the statistical signiﬁcance:

> as.data.frame(anova(fit, test="Chisq")[2,])

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

x 1 7.353132 7 5.012176 0.006694603

The score test seems about right:

> fit <- glm(y~1, family=binomial)

> 2 * pnorm(-abs(glm.scoretest(fit, x)))

[1] 0.01937237



7.4 Goodness-of-Fit Tests with φ Known

7.4.1 The Idea of Goodness-of-Fit

This chapter has so far examined tests of whether particular explanatory

variables should be retained or added to the current model. One would often

like to ask: how many explanatory variables are suﬃcient? When can we

stop testing for new explanatory variables? Goodness-of-ﬁt tests determine

whether the current linear predictor already includes enough explanatory

variables to fully describe the systematic trends in the data. In that case, no

more explanatory variables are useful or necessary. This sort of test is only

possible when φ is known, because it requires a known distribution for the

residual variability.

A goodness-of-ﬁt test compares the current model (Model A say) with an

alternative model (Model B) of a particular type. In this case, Model B is

the largest possible model which can, in principle, be ﬁtted to the data. This

model has as many explanatory variables as data points, so that p



= n,and

is known as the saturated model. Under the saturated model, the ﬁtted values

are all equal to the data values: ˆμ

= y

. This is generally true, regardless of

the speciﬁc explanatory variables in the saturated model, as long at there are



linearly independent predictors, so we talk of the saturated model rather

than a saturated model. The test is on n −p



degrees of freedom, because the

saturated model has n parameters compared to the current model with p



If the goodness-of-ﬁt test is rejected, then this is evidence that the cur-

rent model is not adequate. By “not adequate” we mean that the systematic

component does not explain everything that can be explained, so there must

be other important explanatory variables which are missing from our model.

7.4 Goodness-of-Fit Tests with φ Known 275

7.4.2 Deviance Goodness-of-Fit Test

The residual deviance for the saturated model is zero, so the likelihood ratio

test statistic of the current model versus the saturated model turns out to be

simply the residual deviance D(y, ˆμ) of the current model.

Following the usual results for likelihood ratio tests, it is tempting to treat

the residual deviance as chi-square on n − p



degrees of freedom. However,

the usual large-sample asymptotics do not hold here, because the number of

parameters in the saturated model increases with the number of observations.

Instead, appealing to the saddlepoint approximation is necessary, which we

do in Sect. 7.5.

Example 7.9. The well-known G-test for independence in a two-way contin-

gency table is a deviance goodness-of-ﬁt statistic. 

7.4.3 Pearson Goodness-of-Fit Test

The (chi-square) score test statistic of the current model versus the saturated

model turns out to be the Pearson statistic X

. Following the usual results

for score tests, it is tempting to treat the Pearson statistic as chi-square on

n − p



degrees of freedom, but the usual large-sample asymptotics do not

hold, for the same reason as for the residual deviance. Instead appealing to

the Central Limit Theorem is necessary, which we do in Sect. 7.5.

Example 7.10. The well-known Pearson chi-square test for independence in

a two-way contingency table is a Pearson goodness-of-ﬁt statistic. 

Example 7.11. In modern molecular genetics research, it is common to study

transgenic mice which have mutations in a speciﬁed gene but which are oth-

erwise identical to normal mice. In a study at the Walter and Eliza Hall

Institute of Medical Research (Melbourne), a number of heterozygote mice

(having one normal allele A and one mutant allele a for the gene of inter-

est) were mated together. Simple Mendelian inheritance would imply that

the AA (normal), Aa (heterozygote mutant) and aa (homozygote mutant)

genotypes should occur in the oﬀspring in the proportions 1/4, 1/2 and 1/4

respectively. A particular experiment gave rise to the numbers of oﬀspring

given in Table 7.2.

Are these numbers compatible with Mendelian inheritance? We answer

this question by ﬁtting a Poisson glm for which the ﬁtted values are in the

Mendelian proportions:

> y <- c(15, 26, 4); x <- c(1/4, 1/2, 1/4)

> fit <- glm( y ~ 0+x, family=poisson)

276 7 Generalized Linear Models: Inference

Tabl e 7 .2 The number of oﬀspring mice of each genotype from matings between Aa

heterozygote parents (Example 7.11)

AA Aa aa

15 26 4

Note the 0 to omit the intercept from the linear predictor. Then compute

goodness-of-ﬁt tests:

> pearson.gof <- sum(fit$weights * fit$residuals^2)

> tab <- data.frame(GoF.Statistic=c(fit$deviance, pearson.gof))

> tab$DF <- rep(fit$df.residual, 2)

> tab$P.Value <- pchisq(tab$GoF, df=tab$DF, lower.tail=FALSE)

> row.names(tab) <- c("Deviance", "Pearson"); print(tab, digits=3)

GoF.Statistic DF P.Value

Deviance 12.2 2 0.00227

Pearson 17.5 2 0.00016

Both the deviance and Pearson goodness-of-ﬁt tests reject the null hypothesis

that the model is adequate. The proportion of aa mutants appears to be too

low. One explanation is that the mutation is harmful so that homozygote

mutants tend to die before birth. 

7.5 Small Dispersion Asymptotics

The large sample asymptotics considered earlier are not suﬃcient for

goodness-of-ﬁt tests to be valid. For goodness-of-ﬁt tests, we require distribu-

tional results to hold reasonably well for individual observations. Therefore,

here we consider results which hold when the precision of individual obser-

vations becomes large. We call these results small dispersion asymptotics.

The work-horses of small dispersion asymptotics are the saddlepoint ap-

proximation (for results about the deviance statistics), and the Central Limit

Theorem (for results about Pearson statistics).

The accuracy of the saddlepoint approximation has been previously dis-

cussed (Sect. 5.4.4). We noted that the accuracy of the saddlepoint approxi-

mation to a probability function depended only on y,notμ, for a given edm.

The criterion τ ≤ 1/3 (see Sect. 5.23,p.225) was given to ensure a good

approximation (where τ = φV (y)/(y − boundary)

). We noted in Sect. 5.4.5

that limits did need to placed on μ for the chi-square distributional approx-

imation to hold well for the unit deviance. For a ﬁtted glm, we can cover

both of these conditions by requiring that the criterion τ ≤ 1/3 is satisﬁed

for all y

, i =1,...,n [9]. As a guideline, this generally ensures that both

the responses y

and the ﬁtted values ˆμ

are in the required range for the

approximation to hold.

7.5 Small Dispersion Asymptotics 277

The Central Limit Theorem has a slower convergence rate than the saddle-

point approximation (O(φ

1/2

) instead of O(φ)), so we apply a slightly stricter

criterion, that τ ≤ 1/5 for all observations.

The Pearson statistic (Sect. 6.8.5,p.255) has approximately a chi-square

distribution

∼ χ

n−p



when the Central Limit Theorem holds for individual observations. However,

the Pearson estimator of φ should remain approximately unbiased even for

smaller τ , at least in large sample situations.

The residual deviance has approximately a chi-square distribution

D(y, ˆμ)

∼ χ

n−p



when the saddlepoint approximation holds. This criterion ensures that the

mean-deviance estimator of φ is approximately unbiased. The distributional

approximation is likely to be better for the deviance than for the Pearson

statistic for moderate values of φ. For very small values of φ, the deviance

and Pearson statistics are almost identical.

The guidelines translate into the following rules for common edms. The

saddlepoint approximation is suﬃciently accurate when

• Binomial: min{m

}≥3 and min{m

(1 − y

)}≥3;

• Poisson: min{y

}≥3;

• Gamma: φ ≤ 1/3.

Recall that saddlepoint approximation is exact for normal and inverse Gaus-

sian glms.

The Central Limit Theorem is suﬃciently accurate for individual observa-

tions when

• Binomial: min{m

}≥5 and min{m

(1 − y

)}≥5;

• Poisson: min{y

}≥5;

• Gamma: φ ≤ 1/5.

Of course, residual deviance and Pearson statistic have exact chi-square dis-

tributions for normal linear regression models.

These conditions should be suﬃcient to ensure that the chi-square dis-

tribution approximations for the residual deviance or Pearson statistics are

suﬃciently accurate for routine use. The chi-square approximations might

continue to be good enough for practical use when the criteria are not sat-

isﬁed, depending on the number of observations for which the criteria fail.

Examination of the speciﬁcs of each data situation is recommended in these

cases.

Example 7.12. In Example 7.11, the mouse oﬀspring counts are Poisson with

min{y

} = 4. The saddlepoint approximation guideline is satisﬁed, but that

278 7 Generalized Linear Models: Inference

for the Central Limit Theorem is not quite, so the deviance goodness-of-ﬁt

test is more reliable than the Pearson test in this case. 

Example 7.13. The noisy miner data (Example 6.5,p.249) contains several

zero counts, so small dispersion asymptotics do not apply for a Poisson edm.

Neither the deviance nor Pearson goodness-of-ﬁt tests are reliable for these

data. 

7.6 Inference for Coeﬃcients When φ Is Unknown

7.6.1 Wald Tests for Single Regression Coeﬃcients

When φ is unknown, Wald tests are similar to the case with φ known

(Sect. 7.2.1) except that an estimator of φ must be used to compute the

standard errors. The Wald statistic to test the null hypothesis H

: β

= β

becomes

T =

− β

se(

)

where now the standard error se(

)=sv

involves a suitable estimator s

of φ (6.13). The Pearson estimator s

φ is used by r.

If a consistent estimator of φ is used, and the sample size is very large, the

estimate of φ will be close to the true value and T will be roughly standard

normal under the null hypothesis. In small or moderate sized samples, a better

approximation is to treat T as following a t-distribution with n−p



degrees of

freedom. The result for normal linear regression, in which T -statistics follow

t-distributions exactly, is a special case.

In r, using the summary() command shows that the values of Z (or T if

φ is unknown), se(

) and the two-tailed P -values for testing H

: β

=0for

each ﬁtted regression coeﬃcient. If φ is known, the Wald statistic is labelled

z and the P-values are computed by referring to a N(0, 1) distribution. If φ is

estimated (by

φ), the Wald statistic is labelled t and the two-tailed P -values

are computed by referring to a t

n−p



distribution. Other estimators of φ may

be used, as shown in Example 7.14, but beware that the dispersion will then

be treated as known.

Example 7.14. Consider the cherry tree data from Example 3.14 (data set:

trees) for modelling the volume y in cubic feet of n = 31 cherry trees. The

model ﬁtted in that example can be summarized using:

> data(trees)

> tr.m2 <- glm( Volume ~ log(Girth) + log(Height),

family=Gamma(link="log"), data=trees )

> printCoefmat(coef(summary(tr.m2)))

7.6 Inference for Coeﬃcients When φ Is Unknown 279

Estimate Std. Error t value Pr(>|t|)

(Intercept) -6.69111 0.78784 -8.4929 3.108e-09 ***

log(Girth) 1.98041 0.07389 26.8021 < 2.2e-16 ***

log(Height) 1.13288 0.20138 5.6255 5.037e-06 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The summary() shows that the regression coeﬃcients for log(Girth) and

log(Height) are non-zero, in the presence of each other. Since the dispersion

φ is very small, the Pearson and mean deviance estimators of φ are very

similar:

> phi.meandev <- deviance(tr.m2) / df.residual(tr.m2)

> phi.pearson <- summary(tr.m2)$dispersion

> c(Mean.deviance=phi.meandev, Pearson=phi.pearson)

Mean.deviance Pearson

0.006554117 0.006427286

r uses the Pearson estimator. To use the mean deviance estimator of φ to

compute the Wald statistics, use:

> printCoefmat(coef(summary(tr.m2, dispersion=phi.meandev)))

Estimate Std. Error z value Pr(>|z|)

(Intercept) -6.691109 0.795578 -8.4104 < 2.2e-16 ***

log(Girth) 1.980412 0.074616 26.5415 < 2.2e-16 ***

log(Height) 1.132878 0.203361 5.5708 2.536e-08 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Note though that r has now conducted z-tests using a normal distribution

instead of t-tests, treating the dispersion as known, meaning that the signif-

icance of the tests is now slightly over-stated.

The r output above tests β

= 0. However, diﬀerent hypotheses may

be more interesting for these data. For example, the theoretical models

developed in Example 3.14 are based on approximating the shape of the

cherry trees as cones or cylinders. Hypotheses of interest may be H

: β

log(π/1728) (suggesting a conical shape) and H

: β

= log(π/576) (suggest-

ing a cylindrical shape). While these tests are not performed automatically

by r, the Wald test computations are easily completed:

> beta0.hat <- coef(summary(tr.m2))[1,"Estimate"]

> beta0.se <- coef(summary(tr.m2))[1,"Std. Error"]

> # Test beta_0 = log(pi/1728) (for a cone)

> beta0.cone <- log( pi/1728 )

> t1 <- ( beta0.hat - beta0.cone ) / beta0.se

> # Test beta_0 = log(pi/576) (for a cylinder)

> beta0.cylinder <- log( pi/576 )

> t2 <- ( beta0.hat - beta0.cylinder ) / beta0.se

> # Compute P-values

> p1 <- 2 * pt( -abs(t1), df=df.residual(tr.m2) )

280 7 Generalized Linear Models: Inference

> p2 <- 2 * pt( -abs(t2), df=df.residual(tr.m2) )

> tab <- array( c(t1, t2, p1, p2), dim=c(2, 2))

> rownames(tab) <- c("Cone:","Cylinder:")

> colnames(tab) <- c("t-scores","P-values"); tab

t-scores P-values

Cone: -0.483750 0.63232520

Cylinder: -1.878206 0.07080348

No strong evidence exists to reject either hypothesis, though the ﬁt of the

cylindrical model is less good than that of the conic. 

7.6.2 Conﬁdence Intervals for Individual Coeﬃcients

When φ is unknown, Wald conﬁdence intervals are similar to the case with φ

known (Sect. 7.2.2) except that an estimator of φ must be used to compute

the standard errors. The 100(1 − α)% Wald conﬁdence interval for β

± t

∗

α/2,n−p



se(

where t

∗

α/2,n−p



is the value of t such that an area α/2 is in each tail of the

t-distribution with n −p



degrees of freedom. The results apply in the large-

sample case, and when the saddlepoint approximation is satisfactory. The r

function confint() computes Wald conﬁdence intervals from ﬁtted glm()

objects. Again, the result for φ unknown is based on t-statistics (using the

Pearson estimate of φ) so that the results for the special case of the normal

linear regression models are exact. Other estimates of φ can be use by setting

the dispersion input in the confint() call.

Example 7.15. For the cherry tree data trees (Example 7.14,p.278), the

Wald conﬁdence intervals for the regression coeﬃcients are found as follows:

> confint(tr.m2)

2.5 % 97.5 %

(Intercept) -8.2358004 -5.139294

log(Girth) 1.8359439 2.124974

log(Height) 0.7364235 1.528266

The theoretical development in Example 3.14 (p. 125) suggest β

≈ 2and

≈ 1. The conﬁdence intervals show that the estimate for β

is reasonably

precise, and contains the value β

= 2; the conﬁdence interval for β

is less

precise, but contains the value β

= 1. Furthermore, from Example 3.14,

the values β

= log(π/1728) = −6.310 (for a cone) and β

= log(π/576) =

−5.211 (for a cylinder) both lie within the 95% conﬁdence interval for β

. 

7.6 Inference for Coeﬃcients When φ Is Unknown 281

* 7.6.3 Conﬁdence Intervals for μ

When φ is unknown, conﬁdence intervals for the ﬁtted values ˆμ are similar

to the case with φ known (Sect. 7.2.3) except that an estimator of φ must

be used to compute the standard errors. We initially work with ˆη = g(ˆμ),

for which var[ ˆη] is easily found (Sect. 6.6). Then, when φ is unknown and an

estimate is used, a 100(1 −α)% Wald conﬁdence interval for η is

ˆη ± t

∗

α/2,n−p



se(ˆη),

where se(ˆη)=



var[ ˆη], and where t

∗

α/2,n−p



isthevaluesuchthatanarea

α/2 is in each tail of the t-distribution with n − p



degrees of freedom. The

conﬁdence interval for μ is found applying the inverse link function (that

is, μ = g

−1

(η)) to the lower and upper limit of the interval found for ˆη.

Rather than explicitly returning the conﬁdence interval, r optionally returns

the standard errors when making prediction using predict() with the in-

put se.fit=TRUE. This information can be used to form conﬁdence intervals.

Note that predict() returns the value of ˆη by default. The ﬁtted values

(and standard errors) are returned by specifying type="response". The con-

ﬁdence interval is necessarily symmetric on the η scale.

Example 7.16. For the trees data trees, suppose we wish to estimate the

mean volume of trees with height 70 ft and girth 15 in. First, we compute the

predictions and standard errors on the scale of the linear predictor:

> out <- predict( tr.m2, newdata=data.frame(Height=70, Girth=15),

se.fit=TRUE)

Then we form the conﬁdence interval for μ by using the inverse of the loga-

rithmic link function:

> tstar <- qt(p=0.975, df=df.residual(tr.m2)) # For 95% CI

> ci.lo <- exp(out$fit - tstar*out$se.fit)

> ci.hi <- exp(out$fit + tstar*out$se.fit)

> c( Lower=ci.lo, Estimate=exp(out$fit), Upper=ci.hi)

Lower.1 Estimate.1 Upper.1

30.81902 32.62157 34.52955

We see that ˆμ =32.62, and that the 95% conﬁdence interval is from 30.82 to

34.53.

This idea can be extended to compute the conﬁdence intervals for the

mean volume of all trees with varying height and girth 15 in:

> newHt <- seq(min(trees$Height), max(trees$Height), by=4)

> newVol <- predict( tr.m2, se.fit=TRUE,

newdata=data.frame(Height=newHt, Girth=15))

> ci.lo <- exp(newVol$fit-tstar*newVol$se.fit)

> ci.hi <- exp(newVol$fit+tstar*newVol$se.fit)

> cbind( newHt, ci.lo, Vol=exp(newVol$fit), ci.hi, width=ci.hi - ci.lo)

282 7 Generalized Linear Models: Inference

newHt ci.lo Vol ci.hi width

1 63 26.33168 28.95124 31.83141 5.499733

2 67 28.88896 31.04230 33.35614 4.467187

3 71 31.45834 33.15002 34.93267 3.474330

4 75 33.93192 35.27358 36.66829 2.736366

5 79 36.10127 37.41225 38.77084 2.669571

6 83 37.87594 39.56537 41.33016 3.454225

7 87 39.40973 41.73232 44.19180 4.782065



7.6.4 Likelihood Ratio Tests to Compare Nested

Models: F -Tests

In Sect. 7.2.4 (p. 269), likelihood ratio tests were developed for comparing

nested models when φ is known. If φ is unknown, an estimate of φ must

be used. With φ unknown, the appropriate statistic for comparing Model A

(with ﬁtted values ˆμ

) which is nested in Model B (with ﬁtted values ˆμ

)is

F =

{D(y, ˆμ

) − D(y, ˆμ

)}/(p



− p



)

, (7.2)

where the models have p



and p



parameters respectively, and s

is some

suitable estimate of φ based on Model B. This is analogous to the linear

regression model case (2.30)(p.63). Estimators of φ considered in Sect. 6.8

include the modiﬁed proﬁle likelihood estimator

, the Pearson estimator

φ, and the mean deviance estimator

φ. The corresponding F -statistics based

on using the three estimators of φ may be written

{D(y, ˆμ

) − D(y, ˆμ

)}/(p



− p



)

(7.3)

F =

{D(y, ˆμ

) − D(y, ˆμ

)}/(p



− p



)

(7.4)

F =

{D(y, ˆμ

) − D(y, ˆμ

)}/(p



− p



)

, (7.5)

where all estimates of φ are based on Model B.

As usual, all three F -statistics are identical for linear regression mod-

els and, in that case, the statistic follows exactly an F -distribution with



−p



,n−p



) degrees of freedom under the null hypothesis that the two

models A and B are equal. For other glms, the F-statistics are approximately

F -distributed under the null hypothesis. The approximation is likely to be

good whenever the denominator of the F -statistic follows a scaled chi-square

distribution, and the conditions for this are discussed in Sect. 7.5. Empiri-

cally, however, the F -distribution approximation for the F -statistic is often

7.6 Inference for Coeﬃcients When φ Is Unknown 283

more accurate than the chi-square approximation to the denominator. For

this reason, the F -test based on the F -statistics tends to be serviceable in a

wide variety of situations.

The choice between the three F -statistics mirrors the choice between the

three estimators discussed in Sect. 6.8.6.

can be expected to have the best

properties but is inconvenient to compute.

F will follow an F -distribution

accurately under the null hypothesis when the saddlepoint approximation

applies (small dispersion asymptotics). In other situations,

F is likely to be

the less biased than

F and is therefore the default statistic used by the glm

functions in r.

Although F -tests are usually used for two-tailed tests, if Model B and

Model A diﬀer by only one coeﬃcient, then we can deﬁne a signed statistic to

test a one-tailed alternative hypothesis about the value of the true coeﬃcient.

Suppose that p



−p



= 1. We can deﬁne a t-statistic from the signed square-

root of F as

t = sign(

1/2

Then t ∼ t

n−p



approximately under the null hypothesis H

: β

=0.

Example 7.17. For a normal glm, the residual deviance is the rss (Sect. 6.4,

p. 248). The F -statistic for comparing two nested models is

F =

(rss

− rss

)/(p



− p



)

which is the usual F -statistic familiar from anova in the linear regression

model case (2.30). 

Example 7.18. Consider the cherry tree data trees and model tr.m2 ﬁt-

ted in Example 7.14. Fit the two explanatory variables log(Girth) and

log(Height) sequentially, and record the residual deviance and residual de-

grees of freedom for each model:

> data(trees)

> tr.m0 <- glm( Volume ~ 1, family=Gamma(link="log"), data=trees)

> tr.m1 <- update(tr.m0,.~.+log(Girth) )

> tr.m2 <- update(tr.m1,.~.+log(Height) )

> c( deviance(tr.m0), deviance(tr.m1), deviance(tr.m2) )

[1] 8.3172012 0.3840839 0.1835153

> c( df.residual(tr.m0), df.residual(tr.m1), df.residual(tr.m2) )

[1] 30 29 28

Then compute the deviances between the models by computing the corre-

sponding changes in the residual deviance (and also compute the residual

degrees of freedom):

> dev1 <- deviance(tr.m0) - deviance(tr.m1)

> dev2 <- deviance(tr.m1) - deviance(tr.m2)

> df1 <- df.residual(tr.m0) - df.residual(tr.m1)

> df2 <- df.residual(tr.m1) - df.residual(tr.m2)

> c( dev1, dev2)

284 7 Generalized Linear Models: Inference

[1] 7.9331173 0.2005686

> c( df1, df2)

[1]11

To compute the F -test statistics as shown in (7.3)–(7.5), ﬁrst an estimate of

φ is needed:

> phi.meandev <- deviance(tr.m2) / df.residual(tr.m2) # Mean dev.

> phi.Pearson <- summary(tr.m2)$dispersion # Pearson

> c("Mean deviance" = phi.meandev, "Pearson" = phi.Pearson )

Mean deviance Pearson

0.006554117 0.006427286

The Pearson and mean deviance estimates are very similar. Likewise, the

F -statistics and corresponding P -values computed using these two estimates

are similar:

> F.Pearson <- c( dev1/df1, dev2/df2 ) / phi.Pearson

> F.meandev <- c( dev1/df1, dev2/df2 ) / phi.meandev

> P.Pearson <- pf( F.Pearson, df1, df.residual(tr.m2), lower.tail=FALSE )

> P.meandev <- pf( F.meandev, df2, df.residual(tr.m2), lower.tail=FALSE )

> tab <- data.frame(F.Pearson, P.Pearson, F.meandev, P.meandev)

> rownames(tab) <- c("Girth","Height")

> print(tab, digits=3)

F.Pearson P.Pearson F.meandev P.meandev

Girth 1234.3 1.05e-24 1210.4 1.38e-24

Height 31.2 5.60e-06 30.6 6.50e-06

These results show that log(Girth) is signiﬁcant in the model, and that

log(Height) is signiﬁcant in the model after adjusting for log(Girth). 

7.6.5 Analysis of Deviance Tables to Compare Nested

Models

When a series of glms is to be compared, the computations discussed in

Sect. 7.6.4 are often arranged in an analysis of deviance table (similar to

the case when φ is known; Sect. 7.2.5). A series of nested models is ﬁtted

to the data, and the residual deviance and residual degrees of freedom for

each model recorded. The changes in the residual deviance and residual de-

grees of freedom are then compiled into the analysis of deviance table.In

r, the analysis of deviance table is produced by the anova() function. The

argument test="F" must be speciﬁed to obtain P -values for deviance diﬀer-

ences relative to F distributions on the appropriate degrees of freedom. In

r,theF -statistics are computed using the Pearson estimator

φ by default

when computing the anova table (the reasons for this choice in r are given

in Sect. 6.8.6). Other estimates of φ can be provided using the dispersion

argument in the anova() call.

7.6 Inference for Coeﬃcients When φ Is Unknown 285

Tabl e 7.3 The analysis of deviance table for model tr.m2 ﬁtted to the cherry tree data,

writing x

for log(Girth) and x

for log(Height) for brevity (Example 7.18)

Change

Source Deviance in df Mean deviance FP-value

Due to x

7.933 1 7.933 1234 < 0.001

Due to x

, adjusted for x

0.2006 1 0.2006 31.21 < 0.001

Residual 0.1835 28

Total 8.317 30

Example 7.19. For the trees data, the information computed in Example 7.18

is usually compiled into an analysis of deviance table (Table 7.3).

Observe that the mean deviance estimator of φ is easy to compute from

the analysis of deviance table (

φ =0.1835/28 = 0.006554), but the Pearson

estimator is used by r. The analysis of deviance table produced by r is:

> anova(tr.m2, test="F")

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 30 8.3172

log(Girth) 1 7.9331 29 0.3841 1234.287 < 2.2e-16 ***

log(Height) 1 0.2006 28 0.1835 31.206 5.604e-06 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Notice that r also reports the residual deviance and residual degrees of free-

dom for each model in addition to the analysis of deviance information. To

base the test on the mean deviance estimator, use the dispersion argument:

> phi.meandev <- deviance( tr.m2) / df.residual(tr.m2)

> anova(tr.m2, test="F", dispersion=phi.meandev)

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 30 8.3172

log(Girth) 1 7.9331 29 0.3841 1210.402 < 2.2e-16 ***

log(Height) 1 0.2006 28 0.1835 30.602 3.168e-08 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The results are very similar for either estimate of φ. 

The order of ﬁtting terms into a model is important when interpreting

the results from the analysis of deviance tables. The order in which terms

are added to the model may aﬀect whether or not they are statistically sig-

niﬁcant. This means that the actual eﬀect of any one variable can only be

stated conditionally on other variables in the model, which impacts on the

interpretation of the eﬀects.

286 7 Generalized Linear Models: Inference

Example 7.20. Consider ﬁtting log(Girth) and log(Height) in reverse or-

der to that of tr.m2:

> tr.rev <- glm( Volume ~ log(Height) + log(Girth),

family=Gamma(link="log"), data=trees)

> anova(tr.rev, test="F")

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 30 8.3172

log(Height) 1 3.5345 29 4.7827 549.92 < 2.2e-16 ***

log(Girth) 1 4.5992 28 0.1835 715.57 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Here, the conclusions are the same when compared to model tr.m2 (the

evidence strongly suggests both regression coeﬃcients are non-zero) but the

F -statistics and the corresponding P -values are not the same. 

7.6.6 Score Tests

Strictly speaking, score tests assume that φ is known, but they can be

used in an approximate sense when φ is unknown simply by substituting

an estimate for φ. By default, the glm.scoretest() function (in package

statmod) uses the Pearson estimator for φ. Other estimates of φ can be used

by using the dispersion argument in the call to glm.scoretest(). As with

Wald tests, we treat the score test statistics as approximately t-distributed

instead of normal when φ is unknown. The score statistic is approxi-

mately t

n−p



distributed under the null hypothesis when an estimator φ is

used.

Example 7.21. (Data set: trees) Consider the cherry tree data again. The

score test can be used to test if log(Girth) and log(Height) are useful in

the model, using the function glm.scoretest() in r package statmod.First

consider log(Height), conditional on log(Girth) appearing in the model:

> library(statmod)

> mA <- glm( Volume ~ log(Girth), family=Gamma(link="log"), data=trees )

> t.Ht <- glm.scoretest( mA, log(trees$Height) )

> p.Ht <- 2 * pt( -abs(t.Ht), df=df.residual(mA) ) # Two-tailed P-value

> tab <- data.frame(Score.stat = t.Ht, P.Value=p.Ht )

> print(tab, digits=3)

Score.stat P.Value

1 3.83 0.00063

7.7 Comparing Wald, Score and Likelihood Ratio Tests 287

Then consider log(Girth), conditional on log(Height) appearing in the

model:

> mB <- glm( Volume ~ log(Height), family=Gamma(link="log"), data=trees)

> t.Girth<- glm.scoretest( mB, log(trees$Girth) )

> p.Girth <- 2 * pt( -abs(t.Girth), df=df.residual(mB) )

> tab <- data.frame(Score.stat = t.Girth, P.Value=p.Girth )

> print(tab, digits=3)

Score.stat P.Value

1 5.22 1.36e-05

The test statistics and two-tailed P -values are somewhat more conservative

than the corresponding Wald test results shown previously (Example 7.14,

p. 278). The conservatism can be partly attributed to fact that the score tests

use dispersion estimates from the null models with one explanatory variable

instead of from the full model with both explanatory variables. Neverthe-

less, the conclusions are the same. The score tests strongly support adding

log(Girth) to the model in the presence of log(Height), and also support

adding log(Height) to the model in the presence of log(Girth).Wecon-

clude that both explanatory variables are needed. 

7.7 Comparing Wald, Score and Likelihood Ratio Tests

The most common tests used in practice with glms are Wald tests for indi-

vidual coeﬃcients and the likelihood ratio tests for comparing nested models.

Wald tests are easily understood because they simply relate the coeﬃcient

estimates to their standard errors and, for this reason, they are routinely

presented as part of the summary output for a glm ﬁt in r. Likelihood ra-

tio tests correspond to deviance diﬀerences and can be computed using the

anova() function in r. Score tests are much less often used, except in their

incarnation as Pearson goodness-of-ﬁt statistics. Score tests deserve perhaps

to be more used than they are—they are a good choice when testing whether

new explanatory variables should be added to the current model.

For normal linear regression models, Wald, score and likelihood ratio

statistics all enjoy exact null distributions regardless of sample size. For glms,

the test statistics have approximate distributions, as discussed in the previ-

ous sections. In general, the distributional approximations for likelihood ratio

tests and score tests tend to be somewhat better than those for Wald tests.

This is particularly true for binomial or Poisson glms when ﬁtted values oc-

cur on or near the boundary of the range of possible values (for example an

exact zero ﬁtted mean for a Poisson glm or ﬁtted proportions exactly zero or

one for a binomial glm). Wald tests are unsuitable in this situation because

some or all of the estimated coeﬃcients become inﬁnitely large (as will be

discussed in Sect. 9.9), yet likelihood ratio tests remain reasonably accurate.

288 7 Generalized Linear Models: Inference

Wald tests and score tests can be used to test either one-tailed or two-tailed

tests for single regression coeﬃcients. Likelihood ratio tests are traditionally

used only for two-sided hypotheses. Nevetheless they too can be used to

test one-tailed hypotheses for single coeﬃcients via signed likelihood ratio

statistics.

7.8 Choosing Between Non-nested GLMs: AIC and BIC

The hypothesis tests discussed in Sects. 7.2.4 and 7.6.4 only apply when the

models being compared are nested models. However, sometimes a researcher

wishes to compare non-nested models. As with linear regression, the aic and

bic may be used to compare non-nested models, though using the aic or bic

does not constitute a formal testing procedure.

Using deﬁnitions (4.34) and (4.35)(p.202), the aic and bic for a glm

with n observations, p



regression parameters and known φ are

aic = −2 × (

,...,

,φ; y)+2p



bic = −2 × (

,...,

,φ; y) + (log n)p



where  is the log-likelihood. Using this deﬁnition, smaller values of the aic

(closer to −∞) represent better models. When φ is unknown,

aic = −2 × (

,...,

φ; y)+2(p



+1)

bic = −2 × (

,...,

φ; y) + (log n)(p



+1),

where

φ is the mle of φ. In fact, r inserts the simple mean deviance es-

timate D(y, ˆμ)/n for φ.Thisisthemle for normal and inverse Gaussian

glms. For gamma glms, this is approximately the mle when the saddlepoint

approximation is accurate.

The deﬁnitions of the aic and bic given above are computed in r using

AIC() and BIC() respectively. The function extractAIC() also computes the

aic and bic using these deﬁnitions for glms, but omits all constant terms

when computing the aic and bic for linear regression models (and so uses the

forms presented in Sect. 2.11). In other words, the results from using AIC()

and BIC() allow comparisons between linear regression models and glms,

but extractAIC() does not. Note that the bic is found using extractAIC()

by specifying the penalty k=log(nobs(y)) where y is the response variable.

(For more information, see Sect. 4.12.)

Example 7.22. For the cherry tree data trees, suppose we wish to compare

the models

Model 1: log μ = β

+2x

+ β

Model 2: log μ = β

+ β

+ x

7.9 Automated Methods for Model Selection 289

writing x

for log(Girth) and x

for log(Height). Note that these models

are not nested. The coeﬃcients for log(Girth) and log(Height) are treated

in turn as an oﬀset (Sect. 5.5.2) by using their theoretical values. First we ﬁt

both models:

> tr.aic1 <- glm( Volume ~ offset(2*log(Girth)) + log(Height),

family=Gamma(link="log"), data=trees)

> tr.aic2 <- glm( Volume ~ log(Girth) + offset(log(Height)),

family=Gamma(link="log"), data=trees)

We can compute the corresponding aics using either extractAIC() or AIC(),

which produce the same answers for glms:

> c(extractAIC(tr.aic1), extractAIC(tr.aic2))

[1] 2.0000 137.9780 2.0000 138.3677

> c( AIC(tr.aic1), AIC(tr.aic2))

[1] 137.9780 138.3677

The aic suggests that the ﬁrst model is preferred for prediction, so prefer the

model which sets the coeﬃcient for log(Girth) to two, and estimating the

coeﬃcient for log(Height). 

7.9 Automated Methods for Model Selection

The same automatic procedures used for normal linear regression (Sect. 2.12.2,

p. 73) can also be used for glms: drop1(), add1() and step(), and in the

same manner. r bases the decisions about model selection on the value of the

aic by default. The same objections remain to automated variable selection

in the glm context as in the linear regression context (Sect. 2.12.3).

Care is needed when applying the automated methods with glms when φ is

estimated, since the estimate of φ is diﬀerent for each model being compared,

and the estimate is not the mle (the simple mean deviance estimate is used).

In other words, the computed aic is only approximate (Sect. 7.8).

Example 7.23. To use an automated procedure for ﬁtting a model to the

cherry tree data (data set: trees), use step() as follows. (This is shown for

illustration only, as such a process is not necessary in this situation.)

> min.model <- glm( Volume~1, data=trees, family=Gamma(link="log"))

> max.model <- glm( Volume~log(Girth) + log(Height),

data=trees, family=Gamma(link="log"))

> m.f <- step( min.model, scope=list(lower=min.model, upper=max.model),

direction="backward")

290 7 Generalized Linear Models: Inference

The backward elimination and stepwise regression procedures are used in the

following way:

> m.b <- step( max.model, scope=list(lower=min.model, upper=max.model),

direction="backward")

> m.s <- step( min.model, scope=list(lower=min.model, upper=max.model),

direction="both")

In this case, all methods suggest the same model, which is the model sug-

gested from a theoretical basis:

> coef(m.s)

(Intercept) log(Girth) log(Height)

-6.691109 1.980412 1.132878



7.10 Using R to Perform Tests

Various r functions are used to conduct inference on a ﬁtted model named,

say, fit produced from a call to glm().

summary(fit):Thesummary() of the model fit prints the following (see

Fig. 6.1): the parameter estimates, with the corresponding standard errors

(or estimated standard errors); the Wald statistic for testing H

: β

0, and the corresponding P -values; the value of φ if φ is ﬁxed, or the

Pearson estimate of φ if φ is unknown; the null deviance (the residual

deviance after ﬁtting just the constant term as an explanatory variable)

and the corresponding degrees of freedom; the residual deviance after

ﬁtting the given model, and the corresponding degrees of freedom; the

aic for the model; and the number of Fisher scoring iterations necessary

for convergence of the irls algorithm.

The output of summary() (for example, out <- summary(fit)) contains

substantial information. out$family displays the edm and the link func-

tion used to ﬁt the model, and out$dispersion displays the value of the

Pearson estimate of φ. coef(out) displays the parameter estimates and

standard errors, plus the z-ort-values (for φ known and unknown respec-

tively) and two-tailed P -values for testing H

: β

= 0. See ?summary.glm

for further information.

summary() uses the Pearson estimator of φ by default; other estimates

can be used by specifying the estimate using dispersion input in

the call to summary(). deviance() returns the deviance of a model,

and df.residual() returns the residual degrees of freedom for the

model.

glm.scoretest(fit, x2): The function glm.scoretest() (available in the

package statmod) is used to conduct score tests to determine if the ex-

planatory variables in x2 should be added to the model fit. The Pearson

7.10 Using R to Perform Tests 291

estimator of φ is used when φ is unknown, but other estimates can be

used by specifying the estimate using dispersion input in the call to

glm.scoretest().

anova():Theanova() function reports the results of comparing nested mod-

els. anova() canbeusedintwoforms:

1. anova(fit): When a single glm model is given as input, an anova

table is produced that sequentially tests the signiﬁcance of each term

as it is added to the model.

2. anova(fit1, fit2, ...): Compare any set of nested glmsbypro-

viding all the models to anova(). The models are then tested against

one another in the speciﬁed order, where models earlier in the list of

models are nested in later models.

anova( ..., test="F") produces P -values by explicitly referring to an

F -distribution when φ is estimated (Sect. 7.6.4). anova( ..., test=

"Chisq") produces P -values by explicitly referring to a χ

distribution

when φ is known (Sect. 7.2.4).

anova() uses the Pearson estimator of φ, but other estimates can be used

by specifying the estimate using dispersion input in the call to anova().

confint(): Returns the 95% Wald conﬁdence interval for all the estimated

coeﬃcients

in the systematic component. For diﬀerent conﬁdence lev-

els, use confint(fit, level=0.99), for example, which creates 99%

conﬁdence intervals. The Pearson estimate of φ is used by default, but

other estimates can be supplied using the dispersion input.

AIC(fit) and BIC(fit): Returns the aic and bic for the given model re-

spectively. The function extractAIC(fit) also returns the aic (as the

second value returned); the bic is computed using extractAIC(fit, k=

log(nobs(y))).

drop1() and add1(): Drops or adds explanatory variables one at a time from

the given model. Decisions are based on the aic by default; F -test results

are displayed by using test="F" and χ

-test results are displayed by using

test="Chisq".Touseadd1(), the second input shows the scope of the

models to be considered.

step(): Uses automated methods for selecting a glm based on the aic.

Common usage is step(object, scope, direction), where direction

is one of "forward" for forward regression, "backward" for backward

elimination, or "both" for stepwise regression. object is an initial glm,

and scope deﬁnes extent of the models to be considered. Sect. 2.12.2

(p. 73) demonstrates the use of step() for the three types of automated

methods.

292 7 Generalized Linear Models: Inference

7.11 Summary

Chapter 7 considers various inference methods for glms.

Wald tests can be used to test for the statistical signiﬁcance of individ-

ual regression coeﬃcients, using a one- or two-tailed alternative (Sect. 7.2.1

when φ is known; Sect. 7.6.1 when φ is unknown). Conﬁdence intervals for

individual regression coeﬃcients are conveniently computed using the Wald

statistic (Sect. 7.2.2 when φ is known, Sect. 7.6.2 when φ is unknown).

Conﬁdence intervals for ˆμ are found by ﬁrst computing conﬁdence intervals

for ˆη, and then applying the inverse link function (that is, μ = g

−1

(η)) to

the lower and upper limit of the interval found for ˆη (Sect. 7.2.3 when φ is

known; Sect. 7.6.3 when φ is unknown).

Two nested glms, say Model A nested in Model B, can be compared us-

ing a likelihood ratio test. When φ is known, the likelihood ratio statistic

is approximately distributed as χ



−p



if n is relatively large compared to



(Sect. 7.2.4). When φ is unknown, the likelihood ratio statistic is approx-

imately distributed as an F -distribution with (p



− p



,n− p



) degrees of

freedom, provided the appropriate estimator of φ is used. The Pearson esti-

mator or the modiﬁed proﬁle likelihood estimator of φ are used in the large

sample case, and the mean deviance estimator of φ is used in the small dis-

persion case (Sect. 7.6.4).

Commonly, a series of nested models is compared using likelihood ratio

tests. The information from these tests are organized into analysis of deviance

tables (Sects. 7.2.5 if φ is known, and 7.6.5 if φ is unknown).

The score test statistic can be used to test the null hypothesis (against

one- or two-tailed alternatives) that a set of covariates are useful predictors

(Sect. 7.2.7 when φ is known; Sect. 7.6.6 when φ is unknown).

The Wald, likelihood ratio and score tests are based on large-sample

asymptotic results, which apply when n is reasonably large (Sect. 7.3).

When φ is known, goodness-of-ﬁt tests can be used to determine if the

linear predictor already includes enough explanatory variables to fully de-

scribe the systematic trends in the data (Sect. 7.4). The saturated model

is the largest possible model which can, in principle, be ﬁtted to the data

(Sect. 7.4.1). The saturated model has as many explanatory variables as ob-

servations (p



= n) and the ﬁtted values are all equal to the responses (ˆμ = y).

The deviance goodness-of-ﬁt test statistic is the residual deviance D(y, ˆμ)

(Sect. 7.4.2). The Pearson goodness-of-ﬁt test statistic is the Pearson statis-

tic X

(Sect. 7.4.3). The distributional assumptions of goodness-of-ﬁt test

statistics rely on small dispersion asymptotic results (the saddlepoint ap-

proximation and the Central Limit Theorem), not large sample asymptotic

results (Sect. 7.5).

The Pearson statistic has an approximate chi-square distribution when

the Central Limit Theorem holds for individual observations (Sect. 7.5, where

guidelines are provided). The residual deviance has an approximate chi-square

7.11 Summary 293

distribution when the saddlepoint approximation holds for individual obser-

vations (Sect. 7.5, where guidelines are provided).

In practice, Wald tests are commonly used for tests about individual co-

eﬃcients, and likelihood ratio tests for comparing nested models (Sect. 7.7).

The likelihood ratio and score tests are recommended over Wald tests for de-

termining if a variable should be included in the model, as the distributional

assumptions of Wald tests are often quite inaccurate. Likelihood ratio tests

are traditionally used to test two-tailed alternative hypotheses (Sect. 7.7).

The aic and bic can be used to compare non-nested glms (Sect. 7.8). Au-

tomated procedures for choosing between models include forward regression,

backward elimination and step-wise regression (Sect. 7.9).

Problems

Selected solutions begin on p. 537.

7.1. A study examined the relationships between weather conditions during

the ﬁrst 21 days posthatch of scaled quail broods and their survival to 21

days of age [5]. A binomial glm was ﬁtted, using the systematic component

log{μ/(1 −μ)} = η, where 0 <μ<1 is the ﬁtted probability that the chicks

survived 21 days. A total of 54 broods were used in the study (Table 7.4).

1. Suggest a model based on the likelihood ratio statistics.

2. Use Wald tests to determine which explanatory variables are signiﬁcant.

3. Interpret the ﬁnal model.

4. Find the 95% conﬁdence interval for the regression coeﬃcient for maxi-

mum temperature.

7.2. To model the number of species (‘species abundance’) of freshwater mus-

sels in a sample of 44 rivers in parts of the usa [6, 10],aPoissonglm

(with a logarithmic link function) was used with these potential explana-

tory variables: the log of the drainage basin area (LA); stepping-stone dis-

tance from the Alabama–Coosa River (AC); stepping-stone distance from the

Apalachicola river (AP); stepping-stone distance from the Savannah River

Tabl e 7.4 The parameter estimates and standard errors for a binomial glm,andthe

likelihood ratio test statistic L when the indicated variable was excluded from the full

model containing all three explanatory variables (Problem 7.1)

Explanatory variable

se(

) L

Minimum temperature during ﬁrst 12 days 0.143 0.19 0.602

Maximum temperature during ﬁrst 7 days 1.247 0.45 14.83

Number days with precipitation during ﬁrst 7 days −0.706 0.45 2.83

294 7 Generalized Linear Models: Inference

Tabl e 7.5 The analysis of deviance table (left) for the species abundance of freshwater

mussels where D

∗

(y, μ) is the residual scaled deviance, and the ﬁtted regression parame-

ters (right) for the main-eﬀects model containing all explanatory variables (Problem 7.2)

Residual deviance Parameters in full model

Model D

∗

(y, μ) Residual df

se(

)

Full main-eﬀects model 35.77 36

− SL 35.90 37 SL −0.0118 0.0326

− AC 35.91 38 AC −0.0212 0.0654

− SV 38.44 39 SV 0.0473 0.0473

− N 39.60 40 N 0.0110 0.0112

− H 50.97 41 H −0.0334 0.0115

− SR 60.26 42 SR −0.0024 0.0007

− AP 77.82 43 AP −0.0222 0.0053

(Note: LA not removed) LA 0.2821 0.0566

(SV); stepping-stone distance from the St Lawrence River (SL); nitrate con-

tent of river water (N); solid residue in river water (SR); and hydronium ion

concentration of river water (H).

1. Suggest a model based on the changes in residual deviance.

2. What method of selecting a model (forward, backward, or step-wise) is

implied by Table 7.5?

3. Use the aic to recommend a model. (Hint: Using (5.26) may prove use-

ful.)

4. Use Wald tests to determine which explanatory variables are signiﬁcant.

5. Give possible reasons to explain why the explanatory variables suggested

for the two models may be diﬀerent for the Wald and likelihood ratio

tests.

6. The ﬁnal Poisson glm chosen in the source is

log ˆμ =0.7219 − 0.0264AP − 0.0022SR − 0.0336H + 0.2773LA, (7.6)

where the standard errors for each coeﬃcient are, respectively, 0.46, 0.005,

0.0006, 0.011 and 0.05. Compute the Wald statistic for each parameter

in this ﬁnal model.

7. Why are the parameter estimates in (7.6) diﬀerent than those in

Table 7.5?

8. Interpret the ﬁnal model.

7.3. A study [11] compared the number of days each week that 82 junior

British and Irish legislators spent in their constituency, by using a Poisson

glm. The dummy variable Nation is coded as 0 for British and 1 for Irish

legislators. The mean number of days spent in their constituency is 1.8in

Britain, and 2.5 in Ireland.

1. Explain why a Poisson glm may not be appropriate for these data, but

why a Poisson glm is probably reasonably useful anyway.

7.11 Summary 295

Tabl e 7.6 The parameter estimates and standard errors from a study of the number

of days per week junior legislators spend in their constituency (Problem 7.3)

Safeness Expectation Present Future Geographic

Constant of seat of punishment role role? proximity Nation

0.23 0.04 0.06 0.01 0.09 0.05 0.30

se(

) 0.13 0.04 0.05 0.03 0.06 0.02 0.07

2. Using the reported results (Table 7.6), determine if there is a diﬀerence

between the number of days spent in the constituency by British and

Irish legislators.

3. Interpret the regression coeﬃcient for Nation.

4. Form a 90% conﬁdence interval for the regression coeﬃcient for Nation.

5. Which terms are statistically signiﬁcant?

6. Write down the full ﬁtted model.

7.4. Children were asked to build towers as high as they could out of cubical

and cylindrical blocks [3, 7]. The number of blocks used and the time taken

were recorded (data set: blocks). In this problem, only consider the number

of blocks used y and the age of the child x. In Problem 6.10,aglm was ﬁtted

for these data.

1. Use a Wald test to determine if age seems necessary in the model.

2. Use a score test to determine if age seems necessary in the model.

3. Use a likelihood ratio test to determine if age seems necessary in the

model.

4. Compare the results from the Wald, score and likelihood ratio tests. Com-

ment.

5. Is the saddlepoint approximation expected to be accurate? Explain.

6. Is the Central Limit Theorem expected to be accurate? Explain.

7. Find the 95% Wald conﬁdence intervals for the regression coeﬃcients.

8. Plot the number of blocks used against age, and show the relationship

described by the ﬁtted model. Also plot the lines indicating the lower and

upper 95% conﬁdence intervals for these ﬁtted values.

7.5. Nambe Mills, Santa Fe, New Mexico [1, 8], is a tableware manufacturer.

After casting, items produced by Nambe Mills are shaped, ground, buﬀed, and

polished. In 1989, as an aid to rationalizing production of its 100 products, the

company recorded the total grinding and polishing times and the diameter

of each item (Table 5.3; data set: nambeware). In this problem, only consider

the item price y and item diameter x. In Problem 6.11,aglm was ﬁtted to

these data.

1. Use a Wald test to determine if diameter is signiﬁcant.

2. Use a score test to determine if diameter is signiﬁcant.

3. Use a likelihood ratio test to determine if diameter is signiﬁcant.

296 REFERENCES

4. Compare the results from the Wald, score and likelihood ratio tests. Com-

ment.

5. Is the saddlepoint approximation expected to be accurate? Explain.

6. Is the Central Limit Theorem expected to be accurate? Explain.

7. Find the 95% Wald conﬁdence intervals for the regression coeﬃcients.

8. Plot the price against diameter, and show the relationship described by

the ﬁtted model. Also plot the lines indicating the lower and upper 95%

conﬁdence intervals for these ﬁtted values.

References

[1] Data Desk: Data and story library (dasl) (2017). URL http://dasl.

datadesk.com

[2] Fisher, S.R.A.: Statistical Methods for Research Workers. Hafner Press,

New York (1970)

[3] Johnson, B., Courtney, D.M.: Tower building. Child Development 2(2),

161–162 (1931)

[4] Maron, M.: Threshold eﬀect of eucalypt density on an aggressive avian

competitor. Biological Conservation 136, 100–107 (2007)

[5] Pleasant, G.D., Dabbert, C.B., Mitchell, R.B.: Nesting ecology and sur-

vival of scaled quail in the southern high plains of Texas. The Journal

of Wildlife Managament 70(3), 632–640 (2006)

[6] Sepkoski, J.J., Rex, M.A.: Distribution of freshwater mussels: Coastal

rivers as biogeographic islands. Systematic Zoology 23, 165–188 (1974)

[7] Singer, J.D., Willett, J.B.: Improving the teaching of applied statistics:

Putting the data back into data analysis. The American Statistician

44(3), 223–230 (1990)

[8] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

[9] Smyth, G.K., Verbyla, A.P.: Adjusted likelihood methods for modelling

dispersion in generalized linear models. Environmetrics 10, 695–709

(1999)

[10] Vincent, P.J., Hayworth, J.M.: Poisson regression models of species

abundance. Journal of Biogeography 10, 153–160 (1983)

[11] Wood, D.M., Young, G.: Comparing constitutional activity by junior

legislators in Great Britain and Ireland. Legislative Studies Quarterly

22(2), 217–232 (1997)

Chapter 8

Generalized Linear Models:

Diagnostics

Since all models are wrong the scientist must be alert to

what is importantly wrong. It is inappropriate to be

concerned about mice when there are tigers abroad.

Box [1, p. 792]

8.1 Introduction and Overview

This chapter introduces some of the necessary tools for detecting violations of

the assumptions in a glm, and then discusses possible solutions. The assump-

tions of the glm are ﬁrst reviewed (Sect. 8.2), then the three basic types of

residuals (Pearson, deviance and quantile) are deﬁned (Sect. 8.3). The lever-

ages are then given in the glm context (Sect. 8.4) leading to the development

of standardized residuals (Sect. 8.5). The various diagnostic tools for check-

ing the model assumptions are introduced (Sect. 8.7) followed by techniques

for identifying unusual and inﬂuential observations (Sect. 8.8). Comments

about using each type of residual and the nomenclature of residuals are given

in Sect. 8.6. We then discuss techniques to remedy or ameliorate any weak-

nesses in the models (Sect. 8.9), including the introduction of quasi-likelihood

(Sect. 8.10). Finally, collinearity is discussed (Sect. 8.11).

8.2 Assumptions of GLMs

The assumptions made when ﬁtting glms concern:

• Lack of outliers: All responses were generated from the same process, so

that the same model is appropriate for all the observations.

• Link function: The correct link function g() is used.

• Linearity: All important explanatory variables are included, and each

explanatory variable is included in the linear predictor on the correct

scale.

• Variance function: The correct variance function V (μ) is used.

• Dispersion parameter: The dispersion parameter φ is constant.

• Independence: The responses y

are independent of each other.

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_8

297

298 8 Generalized Linear Models: Diagnostics

• Distribution: The responses y

come from the speciﬁed edm.

The ﬁrst assumption concerns the suitability of the model overall. The other

assumptions are ordered here from those that aﬀect the ﬁrst moment of the

responses (the mean), to the second moment (variances) to third and higher

moments (complete distribution of y

). Generally speaking, assumptions that

aﬀect the lower moments of y

are the most basic. Compare these to the

assumptions for the (normal) linear regression model (Sect. 3.2). This chapter

discusses methods for assessing the validity of these assumptions.

Importantly, the assumptions are never exactly true. Instead, it is impor-

tant to be aware of the sensitivity of the conclusions to deviations from the

model assumptions. The model assumptions should always be checked after

ﬁtting a model to identify potential problems, and this information used to

improve the model where possible.

8.3 Residuals for GLMs

8.3.1 Response Residuals Are Insuﬃcient for GLMs

The distances y

− ˆμ

are called the response residuals, and are the basis

for residuals in linear regression. The response residuals are inadequate for

assessing a ﬁtted glm, because glms are based on edms where (in general)

the variance depends on the mean. As an example, consider the cherry tree

data (Example 3.14,p.125), and the theory-based model ﬁtted to the data:

> data(trees)

> cherry.m1 <- glm( Volume ~ log(Girth) + log(Height),

family=Gamma(link=log), data=trees)

> coef( cherry.m1 )

(Intercept) log(Girth) log(Height)

-6.691109 1.980412 1.132878

Consider two volumes y

and y

marked on Fig. 8.1. Also shown are the

modelled distributions of the observations for the corresponding ﬁtted values

ˆμ

(based on the gamma distribution). Note that both observations are y

−

ˆμ

= 7 greater than the respective predicted means. However, observation

is in the extreme tail of the ﬁtted distribution, but observation y

is not

in the extreme tail of the distribution, even though the response residuals

− ˆμ

are the same for each case. A new deﬁnition of residuals is necessary.

Ideally, residuals for glms should behave similarly to residuals for linear

regression models, because residuals in that case are familiar and easily inter-

preted. That is, ideally residuals for glms should be approximately normally

distributed with mean zero and constant variance. Response residuals do not

necessarily have constant variance or a normal distribution.

8.3 Residuals for GLMs 299

l l

The modelled relationship between

volume and girth when Height = 80

Girth

Volume

910

= 11.1

15 16

= 18

Fig. 8.1 The cherry tree data. The solid line shows the modelled relationship between

Volume and log(Girth) when Ht=80. Two observations from the gamma glm as ﬁtted

to the cherry tree data are also shown. Observation y

is extreme, but observation y

not extreme, yet the diﬀerence y

− ˆμ

= 7 is the same in both cases. Note that log-scale

is used on the horizontal axis since the covariate is log(Girth) (Sect. 8.3.1)

8.3.2 Pearson Residuals

The most direct way to handle the non-constant variance in edms is to divide

out the eﬀect of non-constant variance. In this spirit, deﬁne Pearson residuals

y − ˆμ



V (ˆμ)/w

where V () is the variance function. Notice that r

is the square root of

the unit Pearson statistic (Sect. 6.8.5). For a ﬁtted glm in r,sayfit,the

Pearson residuals are found using resid(fit, type="pearson"). The Pear-

son residuals are actually the ordinary residuals when the glm is treated

as a least-squares regression model using the working responses and weights

(Sect. 6.7).

The Pearson statistic has an approximate chi-square distribution when

the Central Limit Theorem applies, under the conditions given in Sect. 7.5

(p. 276). Under these same conditions, the Pearson residuals have an approx-

imate normal distribution.

Example 8.1. For the normal distribution, V (μ) = 1 (Table 5.1), and so the

Pearson residuals are r

=(y − ˆμ)

√

w. 

300 8 Generalized Linear Models: Diagnostics

Example 8.2. For the Poisson distribution, V (μ)=μ (Table 5.1), and so the

Pearson residuals are r

=(y − ˆμ)/



ˆμ/w. 

8.3.3 Deviance Residuals

The Pearson residuals are the square root of the unit Pearson statistic. Sim-

ilarly, deﬁne the deviance residuals r

as the signed square root of the unit

deviance (Sect. 5.4):

= sign(y − ˆμ)



wd(y, ˆμ). (8.1)

(The function sign(x)equals1ifx>0; −1ifx<0; and 0 if x = 0.) For a

ﬁtted model in r,sayfit, the deviance residuals are found using resid(fit).

In other words, the deviance residuals are computed by default by resid().

A summary of the deviance residuals is given in the summary() of the output

object produced by glm() (as seen in Fig. 6.1).

The deviance statistic has an approximate chi-square distribution when

the saddlepoint approximation applies, under the conditions given in Sect. 7.5

(p. 276). Under these same conditions, the deviance residuals have an approx-

imate normal distribution.

Example 8.3. Using the unit deviance for the normal distribution (Table 5.1),

the deviance residuals are r

=(y − ˆμ)

√

w. The deviance residuals are the

same as the Pearson residuals for the normal distribution, and only for the

normal distribution. 

Example 8.4. Using the unit deviance for the Poisson distribution (Table 5.1),

the deviance residuals are

= sign(y − ˆμ)



y log



ˆμ



− (y − ˆμ)





8.3.4 Quantile Residuals

The Pearson and deviance residuals have approximate normal distributions as

explained above, with the deviance residuals more likely to be more normally

distributed than the Pearson residuals [12]. When the guidelines in Sect. 7.5

(p. 276) are not met, the Pearson and deviance residuals can be clearly non-

normal, especially for discrete distributions.

8.3 Residuals for GLMs 301

An alternative to Pearson and deviance residuals are the quantile residu-

als [5], which are exactly normally distributed apart from the sampling vari-

ability in estimating μ and φ, assuming that the correct edm is used. The

quantile residual r

for an observation has the same cumulative probability

on a standard normal distribution as y does for the ﬁtted edm. A simple

modiﬁcation involving randomization is needed for discrete edms. For a ﬁt-

ted model in r,sayfit, the quantile residuals are found using qresid(fit),

using the function qresid() from package statmod.

8.3.4.1 Quantile Residuals: Continuous Response

Quantile residuals are best described in the context of an example. Consider

an exponential edm (4.37) (which is a gamma edm with φ = 1) ﬁtted to

data where one observation is y =1.2 with ˆμ = 3. First, determine the

cumulative probability that an observation is less than or equal to y on this

ﬁtted exponential distribution using pexp() (Fig. 8.2, left panel):

> y <- 1.2; mu <- 3

> cum.prob <- pexp(y, rate=1/mu); cum.prob

[1] 0.32968

Then ﬁnd the value of the standard normal variate with the same cumulative

probability using qnorm(); this is the quantile residual (Fig. 8.2, right panel):

> rq <- qnorm(cum.prob); rq

[1] -0.4407971

Exponential cdf

cdf

u = 0.3297

0.0

0.2

0.4

0.6

0.8

1.0

Standard normal cdf

cdf

u = 0.3297

− 3

− 2 − 1 r

0.0

0.2

0.4

0.6

0.8

1.0

Fig. 8.2 Computing the quantile residuals for an exponential edm for an observation

y =1.2, when ˆμ = 3 (Sect. 8.3.4.2)

302 8 Generalized Linear Models: Diagnostics

More formally, let F(y; μ, φ) be the cumulative distribution function (cdf)

of a random variable y (it need not belong to the edm family). The quantile

residuals are

= Φ

−1

{F(y;ˆμ, φ)},

where Φ(·)isthecdf of the standard normal distribution. (For example,

−1

(0.975) = 1.96 and Φ

−1

(0.025) = −1.96.) If φ is unknown, use the Pearson

estimator of φ.

Example 8.5. For the exponential distribution, the probability function is

given in (4.37). The cdf is

F(y)=1−

exp



−



for y>0. The quantile residual is

= Φ

−1



1 −

ˆμ

exp



−

ˆμ





Example 8.6. For the normal distribution, F is the cdf of a normal distri-

bution with mean μ and variance σ

/w. Since Φ

−1

(·)istheinverse of the

standard normal cdf, the quantile residuals are

(y − ˆμ)

√

where s is the estimate of σ. For the normal distribution, r

= r

/s = r

/s.



8.3.4.2 Quantile Residuals: Discrete Response

For discrete edms, a simple modiﬁcation is necessary to deﬁne the quan-

tile residuals. Consider a Poisson edm for the observation y = 1 when

ˆμ =2.6.

Locate the observation y = 1 on the Poisson cdf (Fig. 8.3, left panel).

Since the cdf is discrete at y =1,thecdf makes a discrete jump between

a =0.074 and b =0.267:

>y<-1;mu<-2.6

> a <- ppois(y-1, mu); b <- ppois(y, mu)

> c(a, b)

[1] 0.07427358 0.26738488

Choose a point at random from the shaded area of the plot between a and b:

8.3 Residuals for GLMs 303

Poisson cdf

cdf

l l

0.0

0.2

0.4

0.6

0.8

1.0

l l

u = 0.149

a = 0.074

b = 0.267

Standard normal cdf

cdf

u = 0.149

−3 −2 0 1 2 3r

0.0

0.2

0.4

0.6

0.8

1.0

Fig. 8.3 Computing the quantile residuals for a situation where the observed value is

y =1whenˆμ =2.6 for a Poisson distribution. The ﬁlled circles indicate the value is

included, while a hollow circle indicates the value is excluded (Sect. 8.3.4.2)

> u <- runif(1, a, b); u

[1] 0.1494077

In this example, the chosen random number is u =0.149. Then ﬁnd the value

of a standard normal variate with the same cumulative probability, as in the

continuous edm case (Fig. 8.3, right panel). This standard normal variate is

the quantile residual for that observation:

> rq <- qnorm( u ); rq

[1] -1.038977

In this example, the quantile residual is r

= Φ

−1

(0.149) = −1.039. (Using

the extremities of the interval for u

, the quantile residual will be between

approximately −0.621 and −1.445.)

This randomization is an advantage: the quantile residuals are continu-

ous even for discrete distributions, unlike deviance and Pearson residuals

(Example 8.8; Problem 8.4). As for the continuous case, the quantile residu-

als have an exact standard normal distribution.

Symbolically, let the lower and upper limits of the region in the cdf be

a = lim

↑0

F(y + ;ˆμ, φ)andb = F(y;ˆμ, φ) respectively. (The notation lim

↑0

means the limit as  approaches 0 from below,sothat is always negative.)

Then, deﬁne randomized quantile residuals as

= Φ

−1

(u),

where u is a uniform random variable on the interval (a, b]. For the Poisson

example above, b = F(y =1;ˆμ =2.6), where F is the cdf for the Poisson

distribution. The value of a is the value of the cdf as y approaches but is

less than y =1.Thus,a = lim

↑0

F(y + ;ˆμ =2.6) = F(y =0.2, ˆμ =2.6).

Four replications of the quantile residuals are recommended [5] when used

with discrete distributions because quantile residuals for a discrete response

304 8 Generalized Linear Models: Diagnostics

have a random component. Any features not preserved across all four sets

of residuals are considered artifacts of the randomization. In the discrete

case, quantile residuals are sometimes called randomized quantile residuals,

for obvious reasons.

Quantile residuals are best used in residual plots where trends and pat-

terns are of interest, because y − ˆμ<0 does not necessarily imply r

< 0

(Problem 8.7). Quantile residuals are strongly encouraged for discrete edms

(Example 8.8).

8.4 The Leverages in GLMs

8.4.1 Working Leverages

As previously explained in Sect. 6.7,aglm can be treated locally as a linear

regression model with working responses z

and working weights W

.The

working responses and weights are functions of the ﬁtted values ˆμ

, but, if

we treat them as ﬁxed, we can compute leverages (or hat values) for each

observation exactly as for linear regression (Sect. 3.4.2).

The ith leverage h

is the weight that observation z

receives when com-

puting the corresponding value of the linear predictor ˆη

. If the leverage is

small, this is evidence that many observations, not just one, are contributing

to the estimation of the ﬁtted value. In the extreme case that h

=1,theith

ﬁtted value will be entirely determined by the ith observation, so that ˆη

= z

and ˆμ

= y.

The variance of the working residuals e

= z

− ˆη

can be approximated by

(see Sect.6.7)

var[e

] ≈ φV (ˆμ

)(1 − h

If φ is unknown, a suitable estimate is used to give var[e

]. As in linear

regression, the leverages are computed using hatvalues() in r.

* 8.4.2 The Hat Matrix

In the context of glms, the hat matrix is

H=W

1/2

X(X

WX)

−1

1/2

, (8.2)

where W is the diagonal matrix of weights from the ﬁnal iteration of the

ﬁtting algorithm (Sect. 6.3). The form is exactly the same as used in linear

regression (Sect. 3.4.2), except in the glm case W depends on the ﬁtted values

8.5 Leverage Standardized Residuals for GLMs 305

μ. The leverages (or hat diagonals) h

are the diagonal elements of H, and

are found in r using hatvalues().

8.5 Leverage Standardized Residuals for GLMs

The Pearson, deviance and quantile residuals discussed in Sect. 8.3 are the

basic types of residuals (called raw residuals). As with linear regression, stan-

dardized residuals have approximately constant variance, and are deﬁned

analogously:





φ(1 − h)

y − ˆμ



φV (ˆμ)(1 − h)/w





φ(1 − h)

sign(y − ˆμ)



wd(y, ˆμ)



φ(1 − h)

(8.3)



√

1 − h

where h are the leverages. If φ is unknown, use an estimate of φ (r uses the

Pearson estimate

φ). The standardized deviance residuals are found directly

using rstandard(); the standardized Pearson and quantile residuals must be

computed in r using the formulae above.

The standardized deviance residuals have a useful interpretation. The

square of the standardized deviance residuals is approximately the reduc-

tion in the residual deviance when Observation i is omitted from the data,

scaled by φ (Problem 8.6).

Observe that division by φ (or its estimate) is not needed for the quantile

residuals as the quantile residuals are transformed to the standard normal

distribution with variance one.

Example 8.7. For the model cherry.m1 ﬁtted to the cherry tree data

(Sect. 8.3; data set: trees), compute the three types of raw residuals in

r as follows:

> library(statmod) # Provides qresid()

> rP <- resid( cherry.m1, type="pearson" )

> rD <- resid( cherry.m1 ) # Deviance resids are the default

> rQ <- qresid( cherry.m1 )

Then compute the standardized residuals also:

> phi.est <- summary( cherry.m1 )$dispersion # Pearson estimate

> rP.std <- rP / sqrt( phi.est*(1 - hatvalues(cherry.m1)) )

> rD.std <- rstandard(cherry.m1)

> rQ.std <- rQ / sqrt( 1 - hatvalues(cherry.m1) )

> all.res <- cbind( rP, rP.std, rD, rD.std, rQ, rQ.std )

> head( all.res ) # Show the first six values only

306 8 Generalized Linear Models: Diagnostics

rP rP.std rD rD.std rQ rQ.std

1 0.01935248 0.2620392 0.01922903 0.2603676 0.2665369 0.2893348

2 0.03334904 0.4558288 0.03298537 0.4508579 0.4380951 0.4800656

3 0.01300934 0.1811459 0.01295335 0.1803663 0.1882715 0.2101705

4 -0.01315583 -0.1691519 -0.01321397 -0.1698994 -0.1380666 -0.1423184

5 -0.04635977 -0.6169148 -0.04709620 -0.6267146 -0.5606192 -0.5980889

6 -0.04568564 -0.6188416 -0.04640051 -0.6285250 -0.5519432 -0.5993880

> apply( all.res, 2, var ) # Find the variance of each column

rP rP.std rD rD.std rQ rQ.std

0.005998800 1.013173741 0.006113175 1.032103295 0.950789672 1.031780512

The variance of the quantile residuals is near one since they are mapped to a

standard normal distribution. The standardized residuals are all similar for

this example. 

8.6 When to Use Which Type of Residual

Quantile, deviance and Pearson residuals all have exact normal distributions

when the responses come from a normal distribution, apart from variability in

ˆμ and

φ. The deviance residuals are also exactly normal for inverse Gaussian

glms. However, in many cases neither the Pearson nor deviance residuals can

be guaranteed to have distributions close to normal, especially for discrete

edms. The simple rules in Sect. 7.5 (p. 276) can be used to determine when

the normality can be expected to be suﬃciently accurate.

Quantile residuals are especially encouraged for discrete edms, since plots

using deviance and Pearson residuals may contain distracting patterns (Ex-

ample 8.8). Furthermore, standardizing or Studentizing the residuals is en-

couraged, as these residuals have more constant variance. For some speciﬁc

diagnostic plots, special types of residuals are used, such as partial residuals

and working residuals (Sect. 8.7.3).

8.7 Checking the Model Assumptions

8.7.1 Introduction

As with linear regression models, plots involving the residuals are used for

assessing the validity of the model assumptions for glms. These plots are dis-

cussed in this section. Remedies for any identiﬁed problems follow in Sect. 8.9.

A strategy similar to that used for linear regression is adopted for as-

sessing assumptions with glms. First, check independence when possible

(Sect. 8.7.2). Then, use plots of the residuals against ˆμ and residuals against

each explanatory variable to identify structural problems in the model. In

8.7 Checking the Model Assumptions 307

all these situations, the ideal plots contain no patterns or trends. Finally,

plotting residuals in a Q–Q plot (Sect. 8.8) is convenient for detecting large

residuals.

8.7.2 Independence: Plot Residuals Against Lagged

Residuals

Independence of the responses is the most important assumption. Indepen-

dence of the responses is usually a result of how the data are collected, so

is often impossible to detect using residuals. As for linear regression, inde-

pendence is, in most cases, best assessed from understanding the process

by which the data were collected. However, if the data are collected over

time, independence can be checked by plotting residuals against the previous

residual in time. Ideally, the plots show no pattern under independence. If

the data are spatial, independence can be checked by plotting the residuals

against spatial explanatory variables (such as latitude and longitude). Again,

the ideal plots show no pattern under independence.

The discussion for linear regression is still relevant (Sect. 3.5.5,p.106),

including the typical plots in Fig. 3.8.

8.7.3 Plots to Check the Systematic Component

Plots of the residuals against the ﬁtted values ˆμ and the residuals against

are the main tools for diagnostic analysis. Using either the standardized

deviance or quantile residuals is preferred in these plots because they have ap-

proximately constant variance. Quantile residuals are especially encouraged

for discrete edms to avoid distracting patterns in the residuals (Example 8.8).

Two features of the plots are important:

• Trends: Any trends appearing in these plots indicate that the systematic

component can be improved. This could mean changing the link function,

adding extra explanatory variables, or transforming the explanatory vari-

ables.

• Constant variation: If the random component is correct (that is, the cor-

rect edm is used), the variance of the points is approximately constant.

The plots can be constructed in r using plot(),orusingscatter.smooth()

which also adds a smoothing curve to the plots which may help detect

trends. Detecting trends in the plots is often easier if the ﬁtted values ˆμ

are spread out more evenly horizontally. This is achieved by using the appro-

priate variance-stabilizing transformation of ˆμ (Table 5.2), often called the

constant-information scale in this context (Table 8.1).

308 8 Generalized Linear Models: Diagnostics

Tabl e 8.1 The constant-information scale transformations of ˆμ for common edmsfor

use in residual plots (Sect. 8.7.3)

edm Scale edm Scale

Binomial: sin

−1

√

ˆμ Inverse Gaussian: 1/

√

ˆμ

Poisson:

√

ˆμ Tweedie (V (μ)=μ

): ˆμ

(2−ξ)/2

Gamma: log ˆμ

If the evidence shows problems with the systematic component, then the

cause may be an incorrect link function, or an incorrect linear predictor (for

example, important explanatory variables are missing, or covariates should

be transformed), or both. To further examine the link function, an informal

check is to plot the working responses (6.9)

=ˆη

dη

dμ

− ˆμ

)

against ˆη

. If the link function is appropriate, then the plot should be roughly

linear [10, §12.6.3]. If a noticeable curvature is apparent in the plot, then

another choice of link function should be considered. The working responses

are found in r using that z

= e

+ˆη

, where e

are the working residuals

(Sect. 6.7), found in r using resid(fit, type="working"). Other methods

also exist for evaluating the choice of link function [2, 13].

To determine if covariate x

is included on the incorrect scale, use partial

residuals

= e

, (8.4)

found in r using resid(fit, type="partial"). This command produces an

n × p array holding the partial residuals for each explanatory variable x

the p columns. A plot of u

against x

(called a component-plus-residual plot

or partial residual plot) is linear if x

is included on the correct scale. The r

function termplot() can also be used to produce partial residual plots, as in

linear regression. If many explanatory variables are included on the incorrect

scale, the process of examining the partial residual plots for each explanatory

variables is iterative: one covariate at a time is ﬁxed, and the partial residual

plots re-examined.

Example 8.8. A binomial glm with a logit link function was used to model

60 observations each with a sample size of 3 (that is, m = 3). The systematic

component of the ﬁtted model assumed η = log{μ/(1 − μ)} = β

+ β

x for

the covariate x. After ﬁtting the model, the plot of quantile residuals against

x shows a curved trend (Fig. 8.4, top left panel), indicating that the model is

inadequate. Interpreting the deviance residuals is diﬃcult (Fig. 8.4, top right

panel), as the data lie on parallel curves, corresponding to the four possible

values of y.

8.7 Checking the Model Assumptions 309

−0.3

−0.2

−0.1

0.0

0.1

0.2

0.3

−3

−2

−1

Linear model:

quantile residuals

Explanatory variable

Quantile residuals

−0.3

−0.2

−0.1

0.0

0.1

0.2

0.3

−3

−2

−1

Linear model:

deviance residuals

Explanatory variable

Deviance residuals

−0.3

−0.2

−0.1

0.0

0.1

0.2

0.3

−3

−2

−1

Quadratic model:

quantile residuals

Explanatory variable

Quantile residuals

−0.3

−0.2

−0.1

0.0

0.1

0.2

0.3

−3

−2

−1

Quadratic model:

deviance residuals

Explanatory variable

Deviance residuals

Fig. 8.4 The residuals from a ﬁtted binomial glm. Top panels: the binomial glm with

a linear systematic component plotted against the explanatory variable; bottom pan-

els: the binomial glm with a quadratic systematic component plotted against the ex-

planatory variable; left panels: the quantile residuals; right panel: the deviance residuals

(Example 8.8)

After ﬁtting the systematic component η = log{μ/(1 − μ)} = β

+ β

x +

, the plot of quantile residuals against x (Fig. 8.4, bottom left panel)

shows no trend and indicates the model now ﬁts well. The deviance residuals

still contain distracting parallel curves (Fig. 8.4, bottom right panel) that

make any interpretation diﬃcult. The data actually are randomly generated

from a binomial distribution so that η truly depends quadratically on x. (This

example is based on [5].) 

Example 8.9. Consider the model cherry.m1 ﬁtted to the cherry tree data

(Example 3.14; data set: trees). We now examine the plots of r



against ˆμ,

against log(Girth) and against log(Height) (Fig. 8.5, top panels):

310 8 Generalized Linear Models: Diagnostics

2.5 3.0 3.5 4.0

−2

−1

log(Fitted values)

Standardized deviance residual

2.2 2.6 3.0

−2

−1

log(Girth)

Standardized deviance residual

4.15 4.25 4.35 4.45

−2

−1

log(Height)

Standardized deviance residual

2.5 3.0 3.5 4.0

2.5

3.0

3.5

4.0

Working responses, z

Linear predictor

8121620

−0.5

0.0

0.5

Girth

Partial for log(Girth)

65 70 75 80 85

−0.5

0.0

0.5

Height

Partial for log(Height)

Fig. 8.5 Diagnostic plots for Model cherry.m1 ﬁtted to the cherry tree data. Top left

panel: r



against log ˆμ

; top centre panel: r



against log(Girth); top right panel: r



against log(Height); bottom left panel: ˆη against z; bottom centre panel: the partial

residual plot for girth; bottom right panel: the partial residual plot for height (Exam-

ple 8.9)

> scatter.smooth( rstandard(cherry.m1) ~ log(fitted(cherry.m1)), las=1,

ylab="Standardized deviance residual", xlab="log(Fitted values)" )

> scatter.smooth( rstandard(cherry.m1) ~ log(trees$Girth), las=1,

ylab="Standardized deviance residual", xlab="log(Girth)" )

> scatter.smooth( rstandard(cherry.m1) ~ log(trees$Height), las=1,

ylab="Standardized deviance residual", xlab="log(Height)" )

(The constant-information scale (Table 8.1) is the logarithmic scale for the

gamma distribution, as used in the top left panel.) The plots appear approxi-

mately linear, but the variance of the residuals for smaller values of ˆμ may be

less than for larger values of ˆμ. The plot of z

against ˆη

is also approximately

linear (Fig. 8.5, bottom left panel) suggesting a suitable link function:

> z <- resid(cherry.m1, type="working") + cherry.m1$linear.predictor

> plot( z ~ cherry.m1$linear.predictor, las=1,

xlab="Working responses, z", ylab="Linear predictor")

> abline(0, 1) # Adds line of equality

8.7 Checking the Model Assumptions 311

The plot of the partial residual (Fig. 8.5, bottom centre and right panels)

suggest Girth and Height are included on the appropriate scale:

> termplot(cherry.m1, partial.resid=TRUE, las=1)

The line shown on each termplot() represents is the ideal relationship, so

in both cases the plots suggest the model is adequate. 

8.7.4 Plots to Check the Random Component

The choice of random component for a glm is usually based on an under-

standing of the data type: proportions of cases are modelled using binomial

glms, and counts by a Poisson glm, for example. However, Q–Q plots may

be used to determine if the choice of distribution is appropriate [5]. Quantile

residuals are used for these plots, since quantile residuals have an exact nor-

mal distribution (apart from sampling variability in estimating μ and φ)if

the correct edm has been chosen.

Example 8.10. Consider the model cherry.m1 (Sect. 8.3) ﬁtted to the cherry

tree data (Example 3.14; data set: trees). A Q–Q plot of the quantile resid-

uals (Fig. 8.6) shows that using a gamma glm seems reasonable.

> qr.cherry <- qresid( cherry.m1 )

> qqnorm( qr.cherry, las=1 ); qqline( qr.cherry)



−2 −1 0 1 2

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

Fig. 8.6 The Q–Q plot of quantile residuals for Model cherry.m1 ﬁtted to the cherry

tree data (Example 8.10)

312 8 Generalized Linear Models: Diagnostics

8.8 Outliers and Inﬂuential Observations

8.8.1 Introduction

As for linear regression models, outliers are observations inconsistent with the

rest of the data, and inﬂuential observations are outliers that substantially

change the ﬁtted model when removed from the data set. The tools used

to identify outliers (Sect. 3.6.2) and inﬂuential observations (Sect. 3.6.3)in

linear regression models are also used for glms, using results from the ﬁnal

step of the irls algorithm (Sect. 6.3), as discussed next.

8.8.2 Outliers and Studentized Residuals

For glms, as with linear regression models, outliers are identiﬁed as obser-

vations with unusually large residuals (positive or negative); the Q–Q plot

is often convenient for doing this. Standardized deviance residuals are com-

monly used, though the use of quantile residuals are strongly encouraged for

discrete data.

As for linear regression, Studentizing the residuals may also be useful

(Sect. 3.6.2). For glms, computing Studentized deviance residuals requires

reﬁtting the original model n further times, when each observation is omit-

ted one at a time. For each model without Observation i, the reduction in the

deviance is computed. Fitting n + 1 models is necessary to do this, which is

computationally expensive, and is avoided by approximating the Studentized

residuals [18]byusing



= sign(y

− ˆμ

)



D,i

1 − h

P,i



If φ is unknown, estimate φ using

(i)

D(y, ˆμ) − r

D,i

/(1 − h

)

n − p



− 1

which approximates the mean deviance estimate of φ in the model without

Observation i (written

(i)

). The approximate Studentized deviance residuals

can be found in r using rstudent(), as used for linear regression models.

Example 8.11. Consider the cherry tree data and the model cherry.m1 ﬁtted

in Sect. 8.3 (data set: trees). Compute the raw quantile residuals, raw dev-

iance residuals, standardized deviance residuals, and Studentized residuals:

8.8 Outliers and Inﬂuential Observations 313

> library( statmod ) # To compute quantile residuals

> rs <- cbind( rD=resid(cherry.m1), "r'D"=rstandard(cherry.m1),

"r''"=rstudent(cherry.m1), rQ=qresid(cherry.m1))

> head(rs)

rD r'D r'' rQ

1 0.01922903 0.2603676 0.2537382 0.2665369

2 0.03298537 0.4508579 0.4408129 0.4380951

3 0.01295335 0.1803663 0.1756442 0.1882715

4 -0.01321397 -0.1698994 -0.1652566 -0.1380666

5 -0.04709620 -0.6267146 -0.6125166 -0.5606192

6 -0.04640051 -0.6285250 -0.6140386 -0.5519432

> apply( abs(rs), 2, max) # The maximum absolute for each residual

rD r'D r'' rQ

0.166763 2.197761 2.329122 2.053011

Since φ is small in this case, the saddlepoint approximation is suitable

(Sect. 5.4.4), and the quantile, standardized and Studentized residuals are

very similar. No large residuals exist. 

8.8.3 Inﬂuential Observations

Inﬂuential observations are outliers with high leverage. The measures of in-

ﬂuence used for linear regression models, such as Cook’s distance D, dffits,

dfbetas and the covariance ratio, are approximated for glms by using re-

sults from the ﬁnal iteration of the irls algorithm (Sect. 6.7).

An approximation to Cook’s distance for glmsis

D ≈



1 − h



φp



)



1 − h

(8.5)

as computed by the function cooks.distance() in r, where the Pearson

estimator

φ of φ is used if it is unknown. Thus, Cook’s distance is a combina-

tion of the size of the residual (measured by r



) and the leverage (measured

by a monotonic function of h). Applying (8.5) for a linear regression model

produces the same formula for Cook’s distance given in (3.6)(p.110).

dfbetas, dffits, and the covariance ratio cr are computed using the

same formulae as those used in linear regression (Sect. 3.6.3,p.110), using

the deviance residuals and using

(i)

in place of s

(i)

. As for linear regres-

sion models, these statistics can be computed in r using dffits() (for df-

fits), dfbetas() (for dfbetas), and covratio() (for cr). The function

influence.measures() returns dfbetas, dffits, cr, D, and the leverages

h, ﬂagging which are deemed inﬂuential (or high leverage in the case of h)

according to the criteria in Sect. 3.6.3.

314 8 Generalized Linear Models: Diagnostics

Example 8.12. For the model cherry.m1 ﬁtted to the cherry tree data

(Sect. 8.3; data set: trees), inﬂuential observations are identiﬁed using

influence.measures():

> im <- influence.measures(cherry.m1); names(im)

[1] "infmat" "is.inf" "call"

> im$infmat <- round(im$infmat, 3 ); head( im$infmat )

dfb.1_ dfb.l(G) dfb.l(H) dffit cov.r cook.d hat

1 0.015 -0.083 0.005 0.107 1.305 0.004 0.151

2 0.120 -0.082 -0.090 0.197 1.311 0.014 0.167

3 0.065 -0.021 -0.054 0.087 1.385 0.003 0.198

4 -0.011 0.021 0.004 -0.041 1.181 0.001 0.059

5 0.145 0.171 -0.170 -0.228 1.218 0.018 0.121

6 0.186 0.191 -0.212 -0.261 1.261 0.023 0.152

> colSums( im$is.inf )

dfb.1_ dfb.l(G) dfb.l(H) dffit cov.r cook.d hat

0000300

Three observations are identiﬁed as inﬂuential, but only by cr. Since none

of the other measures identify these observations as inﬂuential, we should

not be too concerned. Sometimes, plots of the inﬂuence statistics are useful

(Fig. 8.7):

> cherry.cd <- cooks.distance( cherry.m1)

> plot( cherry.cd, type="h", ylab="Cook's distance", las=1)

> plot( dffits(cherry.m1), type="h", las=1, ylab="DFFITS")

> infl <- which.max(cherry.cd) # The Observation number of largest D

> infl # Which observation?

> cherry.cd[infl] # The value of D for that observation

0.2067211

0 5 10 20 30

0.00

0.05

0.10

0.15

0.20

Index

Cook's distance

0 5 10 20 30

−0.5

0.0

0.5

Index

DFFITS

Fig. 8.7 Identifying inﬂuential observations for model cherry.m1 ﬁtted to the cherry

tree data. Left panel: Cook’s distance; right panel: dffits (Example 8.12)

8.9 Remedies: Fixing Identiﬁed Problems 315

The value of Cook’s distance for Observation 18 is much larger than any

others, but the observation is not identiﬁed as signiﬁcantly inﬂuential. To

demonstrate, we ﬁt the model without Observation 18, then compare the

estimated coeﬃcients:

> cherry.infl <- update(cherry.m1, subset=(-infl) )

> coef(cherry.m1)

(Intercept) log(Girth) log(Height)

-6.691109 1.980412 1.132878

> coef(cherry.infl)

(Intercept) log(Girth) log(Height)

-7.209148 1.957366 1.267528

(The negative sign in subset=(-infl) omits Observation infl from the

data set for this ﬁt only.) The changes are not substantial, apart perhaps

from the intercept. Contrast to the changes in the coeﬃcients when another

observation with a smaller value of D is omitted:

> cherry.omit1 <- update(cherry.m1, subset=(-1) ) # Omit Obs. 1

> coef(cherry.m1)

(Intercept) log(Girth) log(Height)

-6.691109 1.980412 1.132878

> coef(cherry.omit1)

(Intercept) log(Girth) log(Height)

-6.703461 1.986711 1.131840

The coeﬃcients are very similar to those from model cherry.m1 when Ob-

servation 1 is omitted: Observation 1 is clearly not inﬂuential. 

8.9 Remedies: Fixing Identiﬁed Problems

The techniques of Sects. 8.7 and 8.8 identify weaknesses in the ﬁtted model.

This section discusses possible remedies for these weaknesses. The following

strategy can be adopted:

• If the responses are not independent (Sect. 8.7.2), use other methods,

such as generalized estimating equations [7], generalized linear mixed

models [2, 11] or spatial glms[4, 6]. These are beyond the scope of this

book.

• Ensure the correct edm is used (Sect. 8.7.3); that is, ensure the random

component is adequate. For glms, the response data usually suggest the

edm:

– Proportions of totals may be modelled using a binomial edm

(Chap. 9).

– Count data may be modelled using a Poisson or negative binomial

edm (Chap. 10).

316 8 Generalized Linear Models: Diagnostics

– Positive continuous data may be modelled using a gamma or inverse

Gaussian edm (Chap. 11). In some cases, a Tweedie edm may be

necessary (Sect. 12.2.3).

– Positive continuous data with exact zeros may be modelled using a

Tweedie edm (Sect. 12.2.4).

Occasionally, a mean–variance relationship may be suggested that does

notcorrespondtoanedm. In these cases, quasi-likelihood may be used

(Sect. 8.10), or a diﬀerent model may be necessary.

• Ensure the systematic component is correct (Sect. 8.7.3):

– The link function may need to change. Changing the link function

may be undesirable, because this changes the relationship between y

and every explanatory variable, and because only a small number of

link functions are useful for interpretability.

– Important explanatory variables may be missing.

– The covariates may need to be transformed. Partial residual plots

may be used to determine if the covariates are included on the correct

scale (and can be produced using termplot()). Simple transforma-

tions, polynomials in covariates (Sect. 3.10) or data-driven systematic

components based on regression splines (Sect. 3.12) may be necessary

in the model. r functions such as poly(), bs() and ns() are used

for glms in the same way as for linear regression models.

Outliers and inﬂuential observations also may be remedied by making struc-

tural changes to the model. Sometimes, other strategies are needed to accom-

modate outliers and inﬂuential observations, including (under appropriate

circumstances) omitting these observations; see Sect. 3.13.

Example 8.13. A suitable model for the cherry tree data was found in Sect. 8.3

(data set: trees). However, as an example we now consider residual plots

from ﬁtting a naive gamma glm using the default (reciprocal) link function

(Fig. 8.8):

> m.naive <- glm( Volume ~ Girth + Height, data=trees, family=Gamma)

> scatter.smooth( rstandard(m.naive) ~ log(fitted(m.naive)), las=1,

xlab="Fitted values", ylab="Standardized residuals")

> scatter.smooth( rstandard(m.naive) ~ trees$Girth, las=1,

xlab="Girth", ylab="Standardized residuals")

> scatter.smooth( rstandard(m.naive) ~ trees$Height, las=1,

xlab="Height", ylab="Standardized residuals")

> eta <- m.naive$linear.predictor

> z <- resid(m.naive, type="working") + eta

> plot( z ~ eta, las=1,

xlab="Linear predictor, eta", ylab="Working responses, z")

> abline(0, 1, col="grey")

> termplot(m.naive, partial.resid=TRUE, las=1)

(The constant-information scale (Table 8.1) is the logarithmic scale for the

gamma distribution, as used in the top left panel.) The plots of r



against

8.9 Remedies: Fixing Identiﬁed Problems 317

3.0 3.5 4.0 4.5

−4

−3

−2

−1

Fitted values

Standardized residuals

8121620

−4

−3

−2

−1

Girth

Standardized residuals

65 70 75 80 85

−4

−3

−2

−1

Height

Standardized residuals

0.01 0.03 0.05

0.02

0.04

0.06

0.08

Linear predictor, eta

Working responses, z

8121620

−0.03

−0.02

−0.01

0.00

0.01

0.02

0.03

0.04

Girth

Partial for Girth

65 70 75 80 85

−0.03

−0.02

−0.01

0.00

0.01

0.02

0.03

0.04

Height

Partial for Height

Fig. 8.8 Diagnostic plots for Model m.naive ﬁtted to the cherry tree data. Top left

panel: r



against log ˆμ

; top centre panel: r



against Girth; top right panel: r



against

Height; bottom left panel: z against ˆη; bottom centre panel: the partial residual plot for

girth; bottom right panel: the partial residual plot for height (Example 8.13)

log ˆμ (Fig. 8.8, top left panel) and r



against the covariates (top centre and

top right panels) show an inadequate systematic component as shown by the

trends and patterns. The plot of z

against ˆη

(bottom left panel) suggests an

incorrect link function. The partial residual plots (bottom centre and bottom

right panels) suggest the covariates are included in the model incorrectly.

In response to these diagnostic plots, consider the same model but with the

more usual logarithmic link function (Fig. 8.9):

> m.better <- update(m.naive, family=Gamma(link="log"))

> scatter.smooth( rstandard(m.better) ~ log(fitted(m.better)), las=1,

xlab="log(Fitted values)", ylab="Standardized residuals")

> scatter.smooth( rstandard(m.better) ~ trees$Girth, las=1,

xlab="Girth", ylab="Standardized residuals")

> scatter.smooth( rstandard(m.better) ~ trees$Height, las=1,

xlab="Height", ylab="Standardized residuals")

> eta <- m.better$linear.predictor

> z <- resid(m.better, type="working") + eta

> plot( z ~ eta, las=1, las=1,

xlab="Linear predictor, eta", ylab="Working residuals, z")

> abline(0, 1, col="grey")

> termplot(m.better, partial.resid=TRUE, las=1)

The partial residual plots are much improved (Fig. 8.9, bottom centre and

bottom right panels), and the plot of z

against ˆη (bottom left panel) suggests

318 8 Generalized Linear Models: Diagnostics

2.5 3.0 3.5 4.0 4.5

−2

−1

log(Fitted values)

Standardized residuals

8121620

−2

−1

Girth

Standardized residuals

65 70 75 80 85

−2

−1

Height

Standardized residuals

2.5 3.0 3.5 4.0 4.5

2.5

3.0

3.5

4.0

Linear predictor, eta

Working residuals, z

8121620

−0.5

0.0

0.5

1.0

Girth

Partial for Girth

65 70 75 80 85

−0.5

0.0

0.5

1.0

Height

Partial for Height

Fig. 8.9 Diagnostic plots for Model m.better ﬁtted to the cherry tree data. Top left

panel: r



against log ˆμ

; top centre panel: r



against Girth; top right panel: r



against

Height; bottom left panel: z against ˆη; bottom centre panel: the partial residual plot for

girth; bottom right panel: the partial residual plot for height (Example 8.13)

the correct link function is used. However, the plots of r



against log ˆμ (top

left panel) and r



against the covariates (top centre and top right panels)

still suggest a structural problem with the model.

In response to these diagnostic plots, model cherry.m1 could be adopted.

The residual plots from model cherry.m1 then show an adequate model

(Fig. 8.5,p.310). In any case, cherry.m1 has sound theoretical grounds, and

should be preferred anyway. 

8.10 Quasi-Likelihood and Extended Quasi-Likelihood

In rare cases, sometimes the mean–variance relationship for a data set sug-

gests a distribution that is not an edm. However, the theory developed for

glms is all based on distributions in the edm family. However, note that for

edms, the log-probability function has the neat derivative (Sect. 6.2)

∂ log P(μ, φ; y)

∂μ

y −μ

φV (μ)

. (8.6)

8.10 Quasi-Likelihood and Extended Quasi-Likelihood 319

This relationship is used in ﬁtting glms to ﬁnd the estimates

(Sect. 6.2);

the estimates of β

and the standard errors se(

) are consistent given only

the mean and variance information.

Motivated by these results, consider a situation where only the form of the

mean and the variance are known, but no distribution is speciﬁed. Since no

distribution is speciﬁed, no log-likelihood exists. However, analogous to (8.6),

some quasi-probability function

P exists which satisﬁes

∂ log

P(y; μ, φ)

∂μ

y −μ

φV (μ)

, (8.7)

when only the variance function V (·) is known. On integrating,

log

P(y; μ, φ)=

y −u

φV (u)

du.

Suppose we have a series of observations y

, for which we assume E[y

,andvar[y

]=φV (μ

)/w

. Suppose a link-linear predictor for μ

in terms

of regression coeﬃcients β

,asforaglm. Then the quasi-likelihood function

(more correctly, the quasi-log-likelihood) is deﬁned by

Q(y; μ)=



i=1

log

P(y

; μ

,φ/w

The quasi-likelihood Q behaves like a log-likelihood function, but does not

correspond to any probability function. As a result, the aic and related statis-

tics (Sect. 7.8) are not deﬁned for quasi-models. In addition, quantile residu-

als (Sect. 8.3.4) are not deﬁned for quasi-likelihood models since the quantile

residuals require the cdf to be deﬁned.

The unit deviance can be deﬁned for quasi-likelihoods. First, notice that

the unit deviance in (5.12) can be written as

d(y, μ)=2{t(y, y) − t(y, μ)}

{log P(y; y, φ/w) − log P(y; μ, φ/w)}.

Using the quasi-likelihood in place of the log-likelihood,

d(y, μ)=2

log

P(y; y, φ/w) − log

P(y; μ, φ/w)

=2×

y −u

φV (u)/w

y −u

V (u)

du. (8.8)

320 8 Generalized Linear Models: Diagnostics

In this deﬁnition, the unit deviance depends only on the mean and variance.

The total deviance is the (weighted) sum of the unit deviances as usual:

D(y,μ)=



i=1

d(y

,μ

If there exists a genuine edm for which V (μ) is the variance function,

then the unit deviance and all other quasi-likelihood calculations derived

from V (μ) reduce to the usual likelihood calculations for that edm.Thishas

the interesting implication that estimation and inference for glms depends

only on the mean μ and the variance function V (μ). Since quasi-likelihood

estimation is consistent, it follows that estimation for glms is robust against

mis-speciﬁcation of the probability distribution, because consistency of the

estimates and tests is guaranteed as long as the ﬁrst and second moment

assumptions (means and variances) are correct.

Quasi-likelihood gives us a way to conduct inference when there is no edm

for a given mean–variance relationship. To specify a quasi-type model struc-

ture, write quasi-glm(V (μ); Link function), where V (μ) is the identifying

variance function.

The most commonly-used quasi-models are for overdispersed Poisson-like

or overdispersed binomial-like counts. These models vary the usual variance

functions in some way, often by assuming a value for the dispersion φ greater

than one, something which is not possible with the family of edms.

We discuss models for overdispersed Poisson-like counts, called quasi-

Poisson models, at some length in Sect. 10.5.3. Quasi-Poisson models are

speciﬁed in r using glm() with family=quasipoisson(). We discuss models

for overdispersed binomial-like counts, called quasi-binomial models, at some

length in Sect. 9.8. Quasi-binomial models are speciﬁed in r using glm()

with family=quasibinomial(). Other quasi-models are speciﬁed in r using

family=quasi(). For more details, see Sect. 8.13.

Inference for these quasi-models uses the same functions as for glms:

summary() shows the results of the Wald tests, and glm.scoretest() in

package statmod performs a score test. anova() performs the equivalent of

likelihood ratio tests for comparing nested models by comparing the quasi-

likelihood, which essentially compares changes in deviance. Analysis of dev-

iance tests are based on the F-tests since φ is estimated for the quasi-models.

Example 8.14. For a Poisson distribution, var[

y]=μ so that V (μ)=μ.How-

ever, in practice, often the variation in the data exceeds μ. This is called

overdispersion (Sect. 10.5). One solution is to propose the variance structure

var[y]=φμ, but this variance structure does not correspond to any discrete

edm. Using quasi-likelihood,

log

P(y; μ, φ)=

y −u

φu

du =

y log μ − μ

8.11 Collinearity 321

The same algorithms for ﬁtting glms can be used to ﬁt the model based on

this quasi-likelihood. The unit deviance is

d(y, μ)=2

y −u

du =2



y log

− (y − μ)



identical to the unit deviance for the Poisson distribution (Table 5.1,p.221).



In deﬁning the quasi-likelihood, we considered the derivative of log

P with

respect to μ but not φ. Hence the quasi-probability function is deﬁned only

up to terms not including μ. To deduce a complete quasi-probability function,

the saddlepoint approximation can be used. This gives

log

P(y; μ, φ)=−

log{2πφV (y)}−

d(y, μ)

2φ

which we call the extended quasi-log-probability function. Then

(y; μ, φ/w)=



i=1

log

P(y

; μ

,φ/w

)

deﬁnes the extended quasi-likelihood. Solving dQ

(y; μ, φ/w)/dμ =0shows

that the solutions regarding μ are the same as for the quasi-likelihood and

hence the log-likelihood. However, the extended quasi-likelihood has the ad-

vantage that solving dQ

(y; μ, φ/w)/dφ = 0 produces the mean deviance

estimate of φ.

The key use of extended quasi-likelihood is to facilitate the estimation of

extended models which contains unknown parameters in the variance function

V (), or which model some structure for the dispersion φ in terms of covariates.

8.11 Collinearity

As in linear regression (Sect. 3.14), collinearity occurs when at least some of

the covariates are highly correlated with each other, implying they measure

almost the same information.

As discussed in Sect. 3.14, collinearity causes no problems in prediction,

but the parameter estimates

are hard to estimate with precision. Several

equations may be found from which to compute the predictions, all of which

may be eﬀective but which produce diﬀerent interpretations.

322 8 Generalized Linear Models: Diagnostics

Collinearity is most easily identiﬁed by examining the correlations between

the covariates. Any correlations greater than some (arbitrary) value, perhaps

0.7, are of concern. Other methods also exist for identifying collinearity. The

same remedies apply as for linear regression (Sect. 3.14):

• Omitting some explanatory variables from the analysis.

• Combine explanatory variables in the model provided the combination

makes sense.

• Collect more data, if there are observations that can be made that better

distinguish the correlated covariates.

• Use special methods, such as ridge regression [17, §11.2], which are beyond

the scope of this book.

Example 8.15. For the cherry tree data (Example 3.14; data set: trees), the

two explanatory variables are correlated:

> cor( trees$Girth, trees$Height)

[1] 0.5192801

> cor( log(trees$Girth), log(trees$Height) )

[1] 0.5301949

Although correlated (that is, taller trees tend to have larger girths), collinear-

ity is not severe enough to be a concern. 

8.12 Case Study

The noisy miner data [9] have been used frequently in this book (Example 1.5;

nminer). The glm ﬁtted to model the number of noisy miners Minerab from

the number of eucalypt trees Eucs is:

> library(GLMsData); data(nminer)

> nm.m1 <- glm( Minerab ~ Eucs, data=nminer, family=poisson)

> printCoefmat(coef(summary(nm.m1)))

Estimate Std. Error z value Pr(>|z|)

(Intercept) -0.876211 0.282793 -3.0984 0.001946 **

Eucs 0.113981 0.012431 9.1691 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The diagnostic plots (Fig. 8.10) are informative:

> library(statmod) # To find randomized quantile residuals

> qr <- qresid( nm.m1 )

> qqnorm(qr, las=1); qqline(qr)

> plot( qr ~ sqrt(fitted(nm.m1)), las=1 )

> plot( cooks.distance(nm.m1), type="h", las=1 )

> plot( hatvalues(nm.m1), type="h", las=1 )

8.12 Case Study 323

−2 −1 0 1 2

−3

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

High leverage

Large residual

Influential

1.0 1.5 2.0 2.5 3.0 3.5 4.0

−3

−2

−1

Quantile residuals vs fitted

values (on const. inf. scale)

Quantile residuals

0 5 10 15 20 25 30

0.0

0.2

0.4

0.6

0.8

Cook's distance

Index

Threshold

0 5 10 15 20 25 30

0.1

0.2

0.3

0.4

0.5

Hat values

Index

Fig. 8.10 Diagnostic plots for the glm ﬁtted to the noisy miner data. Top left: Q–Q

plot of quantile residuals; top right: quantile residuals against

√

ˆμ (using the constant-

information scale for the Poisson distribution); bottom left: Cook’s distance, with the

threshold for signiﬁcance shown; bottom right: the leverages (Sect. 8.12)

We now locate the observations with the largest leverage, the largest absolute

quantile residual, and the most inﬂuential observation:

> maxhat <- which.max( hatvalues(nm.m1) ) # Largest leverage

> maxqr <- which.max( abs(qr) ) # Largest abs. residual

> maxinfl <- which.max( cooks.distance(nm.m1)) # Most influential

> c( MaxLeverage=maxhat, MaxResid=maxqr, MaxInfluence=maxinfl)

MaxLeverage.11 MaxResid MaxInfluence.17

11 7 17

Only Observation 17 is inﬂuential according to r’s criterion (Sect. 3.6.3):

> which(influence.measures(nm.m1)$is.inf[,"cook.d"] )

In summary, Observation 11 (plotted with a ﬁlled square) has high leverage,

but the residual is small and so it is not inﬂuential; Observation 7 (plotted

with ﬁlled circle) has a large residual, but the leverage is small and so it is not

324 8 Generalized Linear Models: Diagnostics

0 5 10 15 20 25 30 35

Number of eucalypts

Number of noisy miners

lllll lll

High leverage

Large residual

Influential

0 5 10 15 20 25 30 35

Number of eucalypts

Number of noisy miners

lllll lll

Original model

Omitting influential

observation

Fig. 8.11 Plots of the noisy miner data: left: the data plotted showing the location of

three important observations; right: the data plotted with the ﬁtted models, with and

without the inﬂuential observation, Observation 17 (Sect. 8.12)

inﬂuential; Observation 17 (plotted with a ﬁlled triangle) has a reasonably

large residual and leverage, and so it is inﬂuential.

Observe the changes in the regression coeﬃcients after omitting Observa-

tion 17:

> nm.m2 <- glm( Minerab ~ Eucs, family=poisson, data=nminer,

subset=(-maxinfl)) # A negative index removes the obs.

> c( "Original model"=coef(nm.m1), "Without Infl"=coef(nm.m2))

Original model.(Intercept) Original model.Eucs

-0.8762114 0.1139813

Without Infl.(Intercept) Without Infl.Eucs

-1.0112791 0.1247156

The two ﬁtted models appear slightly diﬀerent for transects with larger num-

bers of eucalypts (near Observation 17; Fig. 8.11, right panel):

> plot( Minerab ~ jitter(Eucs), data=nminer,

xlab="Number of eucalypts", ylab="Number of noisy miners")

> newE <- seq( 0, 35, length=100)

> newM1 <- predict( nm.m1, newdata=data.frame(Eucs=newE), type="response")

> newM2 <- predict( nm.m2, newdata=data.frame(Eucs=newE), type="response")

> lines( newM1 ~ newE, lty=1); lines( newM2 ~ newE, lty=2)

These results suggest that the two transects with the largest number of

eucalypts are important for understanding the data. Overdispersion may be

an issue for these data, which we explore in Problem 10.10:

> c( deviance(nm.m1), df.residual(nm.m1) )

[1] 63.31798 29.00000

8.13 Using R for Diagnostic Analysis of GLMs 325

8.13 Using R for Diagnostic Analysis of GLMs

Residuals are computed in r for a ﬁtted glm,sayfit, using:

• Pearson residuals r

: resid(fit, type="pearson").

• Deviance residuals r

: resid(fit), since deviance residuals are the de-

fault.

• Quantile residuals r

: qresid(fit) after loading package statmod.

• Partial residuals u

: resid(fit, type="partial").

• Working residuals e: resid(fit, type="working").

• Response residuals y − ˆμ: resid(fit, type="response").

• Standardized deviance residuals r



: rstandard(fit).

• Studentized deviance residuals r



: approximated using rstudent(fit).

The longer form residuals(fit) is equivalent to resid(fit).Eachtypeof

residual apart from type="partial" returns n values, one for each obser-

vation. Using type="partial" returns an array with n rows and a column

corresponding to each β

(apart from β

Other useful r commands for diagnostics analysis, used in the same way

as for linear regression models, are: fitted(fit) for producing ﬁtted values;

hatvalues(fit) for producing the leverages; qqnorm() for producing Q–Q

plots of residuals; and qqline() for adding reference lines to Q–Q plots.

Measures of inﬂuence are computed for glms using the same r functions

as for linear regression models:

• Cook’s distance D:usecooks.distance(fit).

• dfbetas:usedfbetas(fit).

• dffits:usedffits(fit).

• Covariance ratio cr:usecovratio(fit).

All these measures of inﬂuence, together with the leverages h, are returned

using influence.measures(fit). Observations are ﬂagged according to the

criteria explained in Sect. 3.6.3 (p. 110).

Fitted glms can also plot()-ed (Sect. 3.16,p.146). These commands pro-

duce four residual plots by default; see ?plot.lm.

For remedying problems, the function poly() is used to create orthogonal

polynomials of covariates, and bs() and ns() (both in the r package splines)

for using regression splines in the systematic component.

Fit quasi-glmsinr using the glm() function, but using speciﬁc family

functions:

• quasibinomial() is used to ﬁt quasi-binomial models. The default link

function is the "logit" link function as for binomial glms. "probit",

"cloglog" (complementary log-log), "cauchit" and "log" links are also

permitted, as for binomial glms (Sect. 9.8).

• quasipoisson() is used to ﬁt quasi-Poisson models. The default link

function is the "log" link function as for Poisson glms. "identity" and

"sqrt" links are also permitted, as for Poisson glms (Sect. 10.5.3).

326 8 Generalized Linear Models: Diagnostics

• quasi() is used to ﬁt quasi-models more generally. Because this function

is very general, any of the link functions provided by r are permitted (but

may not all be sensible): "identity" (the default), "logit", "probit",

"cloglog", "cauchit", "log", "identity", "sqrt" and "1/mu^2" are

all permitted. Additional link functions can be deﬁned using the power()

function; for example, link=power(lambda=1/3) uses a link function of

the form μ

1/3

= η.Usinglambda=0 is equivalent to using the logarithmic

link function.

To ﬁt the quasi-models, the variance structure must also be deﬁned,

using for example, family = quasi(link="log", variance="mu"),

which uses the variance function V (μ)=μ. The possible variance struc-

tures permitted for the variance are:

– "constant", the default, for which V (μ) is constant;

– "mu(1-mu)" for which V (μ)=μ(1 −μ);

– "mu" for which V (μ)=μ;

– "mu^2" for which V (μ)=μ

;

– "mu^3" for which V (μ)=μ

Other variance functions can also be speciﬁed by writing appropriate r

functions, but are rarely required and require extra eﬀort and so are not

discussed further.

The aic is not shown in the model summary() for quasi-models, since the aic

is not deﬁned for quasi-models. summary(), anova() and glm.scoretest()

work as usual for quasi-models.

8.14 Summary

Chapter 8 discusses methods for identifying possible violations of assumptions

in glms, and then remedying or ameliorating these problems.

The assumptions for glms are, in order of importance (Sect. 8.2):

• Lack of outliers: The model is appropriate for all observations.

• Link function: The correct link function g() is used.

• Linearity: All important explanatory variables are included, and each

explanatory variable is included in the linear predictor on the correct

scale.

• Variance function: The correct variance function V (μ) is used.

• Dispersion: The dispersion parameter φ is constant.

• Independence: The responses y

are independent of each other.

• Distribution: The responses y

come from the speciﬁed edm.

The main tool for diagnostic analysis is residuals. Pearson, deviance and

quantile residuals can be used for glms (Sect. 8.3). Quantile residuals are

highly recommended for discrete edms. Standardized or Studentized resid-

uals are preferred as they have approximately constant variance (Sect. 8.6).

8.14 Summary 327

For glms, the leverages are the diagonal elements of the hat matrix H =

1/2

X(X

WX)

−1

1/2

(Sect. 8.4.2).

A strategy for diagnostic analysis of glms is (Sects. 8.7 and 8.9):

• Check for independence of the responses (Sect. 8.7.2). If the residuals

show non-independence, use other methods.

• Plot residuals against ˆμ and residuals against each x

(Sect. 8.7.3). If the

variation is not constant, an incorrect edm may have been used.

If a trend exists, the systematic component may need changing: change

the link function, add extra explanatory variables, or transform a covari-

ates.

• To further examine the link function, plot z against ˆη (Sect. 8.7.3).

• To determine if the source of the non-linearity is that covariate x

included on the incorrect scale, plot u

against x

(called a component

plus residual plot or a partial residual plot) (Sect. 8.7.3).

• The choice of distribution can be checked using a Q–Q plot of quantile

residuals (Sect. 8.7.4).

Outliers can be identiﬁed using Studentized residuals (Sect. 8.8). Outliers

and inﬂuential observations also may be remedied by changes made to the

model (Sect. 8.8). Inﬂuential observations can be identiﬁed using Cook’s dis-

tance, dffits, dfbetas or cr (Sect. 8.8).

Quasi-likelihood may be used when a suitable edm cannot be identiﬁed,

but information about the mean and variance is available (Sect. 8.10).

Collinearity occurs when at least some of the covariates are highly corre-

lated with each other, implying they measure almost the same information

(Sect. 8.11).

Problems

Selected solutions begin on p. 539.

8.1. Consider the Poisson distribution.

1. For y = 0, show that the smallest possible value of r

is −

√

wˆμ.

2. For y = 0, show that the smallest possible value of r

is −

√

2wˆμ.

3. For y = 0, what is the smallest value r

can take? Explain.

4. Comment on the normality of the residuals in light of the above results.

8.2. Show that the Pearson residuals for a gamma edm cannot be less than

= −1/

√

w, but have no theoretical upper limit. Use these results to com-

ment on the approximate normality of Pearson residuals for gamma edms.

What range of values can be taken by deviance and quantile residuals?

328 8 Generalized Linear Models: Diagnostics

8.3. Consider the binomial distribution.

1. Determine the deviance residuals for the binomial distribution.

2. In the extreme case m = 1, show that r

will either take the value



2 log(1 − ˆμ)or−

√

2 log ˆμ.

8.4. Use the r function rpois() to generate 1000 random numbers, say y,

from a Poisson distribution with mean 1. Fit a Poisson glm using the system-

atic component y~1. Then, plot the Q–Q plot of the residuals from this model

using the Pearson, deviance and quantile residuals, and comment on the Q–Q

plots produced using the diﬀerent types of residuals. (Remember to generate

more than one set of quantile residuals due to the added randomness.)

8.5. Consider the situation where the observations y come from distributions

with known mean μ and known φ. Show that the Pearson residuals have

mean zero and variance φ for any edm.

8.6. The standardized deviance residual r



D,i

is approximately the reduction

in the residual deviance when Observation i is omitted from the data. Demon-

strate this in r using the trees data as follows.

• Fit the model cherry.m1 (Sect. 8.3.1). Compute the residual deviance,

the Pearson estimate of φ, and the standardized deviance residuals from

this model.

• Omit Observation 1 from trees, and reﬁt the model. Call this model

cherry.omit1.

• Compute the diﬀerence between the residual deviance for the full model

cherry.m1 and for model cherry.omit1. Show that this diﬀerences di-

vided by the Pearson estimate of φ is approximately the standardized

deviance residuals squared.

Repeat the above process for every observation i. At each iteration, call this

model cherry.omiti. Then, compute the diﬀerence between the deviance for

the full model cherry.lm and for model cherry.omiti. Show that these dif-

ferences divided by φ are approximately the standardized residuals squared.

8.7. Consider the exponential distribution (4.37) deﬁned for y>0.

1. When μ =3.5andy =1.5, compute the Pearson, deviance and quantile

residuals when the weights are all one.

2. When μ =3.5andy =3.5, compute the Pearson, deviance and quantile

residuals when the weights are all one.

3. Comment on what the above shows.

8.8. Consider a transformation A(y) of a response variable y.

1. Expand A(y)aboutμ using the ﬁrst two terms of the Taylor series to

show that A(y) − A(μ) ≈ A



(μ)(y −μ).

8.14 Summary 329

2. Using the previous result, compute the variance of both sides to show

that

A(y) − A(μ)



(μ)



V (μ)

called the Anscombe residual [10, 12], has a variance of φ approximately.

3. For glms, A(t)=

V (t)

−1/3

(t)dt, where V (μ) is the variance function.

Hence show that the Anscombe residuals for the Poisson distribution are

3(y

2/3

− μ

2/3

)

2μ

1/6

4. Compute the Anscombe residuals for the gamma and inverse Gaussian

distributions.

8.9. Suppose a situation implies a variance function of the form V (μ)=

(1 − μ)

, where 0 <μ<1 (for example, see [10, §9.2.4]). This variance

function does not correspond to any known edm.

1. Deduce the quasi-likelihood.

2. Deduce the unit deviance.

8.10. A study [16] counted the number of birds from four diﬀerent species of

seabirds in ten diﬀerent quadrats in the Anadyr Strait (oﬀ the Alaskan coast)

during summer, 1998 (Table 8.2; data set: seabirds). Because the responses

are counts, a Poisson glm may be appropriate.

1. Fit the Poisson glm with a logarithmic link function, using the systematic

component Count ~ Species + factor(Quadrat).

2. Using the guidelines in Sect. 7.5 to determine when the Pearson and dev-

iance residuals are expected to be adequate or poor.

3. Using this model, plot the deviance residuals against the ﬁtted values,

and also against the ﬁtted values transformed to the constant-information

scale. Using the plots, determine if the model is adequate.

4. Using the same model, plot the quantile residuals against the ﬁtted values,

and also against the ﬁtted values transformed to the constant-information

scale. Using the plots, determine if the model is adequate.

5. Comparing the plots based on the deviance and quantile residuals, which

type of residual is easier to interpret?

8.11. Children were asked to build towers as high as they could out of cubical

and cylindrical blocks [8, 14]. The number of blocks used and the time taken

were recorded (data set: blocks). In this problem, only consider the number

of blocks used y and the age of the child x.

In Problem 6.10,aglm was ﬁtted for these data. Perform a diagnostic

analysis, and determine if the model is suitable.

330 REFERENCES

Tabl e 8.2 The number of each species of seabird counted in ten quadrats in the Anadyr

Strait during summer, 1998 (Problem 8.10)

Quadrat

Species12345678910

Murre 0 0 0 1 1 0 0 1 1 3

Crestedauklet000231501 5

Leastauklet120000132 3

Puﬃn101100311 0

8.12. Nambe Mills, Santa Fe, New Mexico [3, 15], is a tableware manufac-

turer. After casting, items produced by Nambe Mills are shaped, ground,

buﬀed, and polished. In 1989, as an aid to rationalizing production of its 100

products, the company recorded the total grinding and polishing times and

the diameter of each item (Table 5.3; data set: nambeware).

In Problem 6.11,aglm was ﬁtted to these data. Perform a diagnostic

analysis, and determine if the model is suitable.

8.13. In Problem 3.24 (p. 157), a linear regression model was ﬁtted to artiﬁ-

cial data (data set: triangle), generated so that μ =



+ x

;thatis,x

and x

are the lengths of the sides of a right-angled triangle, and E[y]=μ is

the length of the hypotenuse (where some randomness has been added).

1. Based on the true relationships between the variables, write down the

corresponding systematic component for ﬁtting a glm for modelling the

hypotenuse. What link function is necessary?

2. Fit an appropriate glm to the data, using the normal and gamma distri-

butions to model the randomness. Which glm is preferred?

References

[1] Box, G.E.P.: Science and statistics. Journal of the American Statistical

Association 71, 791–799 (1976)

[2] Breslow, N.E., Clayton, D.G.: Approximate inference in generalized lin-

ear mixed models. Journal of the American Statistical Association

88(421), 9–25 (1993)

[3] Data Desk: Data and story library (dasl) (2017). URL http://dasl.

datadesk.com

[4] Diggle, P.J., Tawn, J.A., Moyeed, R.A.: Model-based geostatistics. Ap-

plied Statistics 47(3), 299–350 (1998)

[5] Dunn, P.K., Smyth, G.K.: Randomized quantile residuals. Journal of

Computational and Graphical Statistics 5(3), 236–244 (1996)

REFERENCES 331

[6] Gotway, C.A., Stroup, W.W.: A generalized linear model approach to

spatial data analysis and prediction. Journal of Agricultural, Biological

and Environmental Statistics 2(2), 157–178 (1997)

[7] Hardin, J.W., Hilbe, J.M.: Generalized Estimating Equations. Chapman

and Hall/CRC, Boca Raton (2012)

[8] Johnson, B., Courtney, D.M.: Tower building. Child Development 2(2),

161–162 (1931)

[9] Maron, M.: Threshold eﬀect of eucalypt density on an aggressive avian

competitor. Biological Conservation 136, 100–107 (2007)

[10] McCullagh, P., Nelder, J.A.: Generalized Linear Models, second edn.

Chapman and Hall, London (1989)

[11] McCulloch, C.E.: Generalized linear mixed models. Institute of Mathe-

matical Statistics (2003)

[12] Pierce, D.A., Shafer, D.W.: Residuals in generalized linear models. Jour-

nal of the American Statistical Association 81, 977–986 (1986)

[13] Pregibon, D.: Goodness of link tests for generalized linear models. Ap-

plied Statistics 29(1), 15–24 (1980)

[14] Singer, J.D., Willett, J.B.: Improving the teaching of applied statistics:

Putting the data back into data analysis. The American Statistician

44(3), 223–230 (1990)

[15] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

[16] Solow, A.R., Smith, W.: Detecting in a heterogenous community sam-

pled by quadrats. Biometrics 47(1), 311–317 (1991)

[17] Weisberg, S.: Applied Linear Regression. John Wiley and Sons, New

York (1985)

[18] Williams, D.A.: Generalized linear models diagnostics using the deviance

and single-case deletions. Applied Statistics 36(2), 181–191 (1987)

Chapter 9

Models for Proportions: Binomial

GLMs

We believe no statistical model is ever ﬁnal; it is simply a

placeholder until a better model is found.

Singer and Willett [22, p. 105]

9.1 Introduction and Overview

Chapters 5–8 develop the theory of glms in general. This chapter focuses on

one speciﬁc glm: the binomial glm. The binomial glm is the most commonly

used of all glms. It is used to model proportions, where the proportions are

obtained as the number of ‘positive’ cases out of a total number of inde-

pendent cases. We ﬁrst compile important information about the binomial

distribution (Sect. 9.2), then discuss the common link functions used for bi-

nomial glms (Sect. 9.3), and the threshold interpretation of the link function

(Sect. 9.4). We then discuss model interpretation in terms of odds (Sect. 9.5),

and how binomial glms can be used to estimate the median eﬀective dose

ed50 (Sect. 9.6). The issue of overdispersion is then discussed (Sect. 9.8), fol-

lowed by a warning about a potential problem with parameter estimation in

binomial glms (Sect. 9.9). Finally, we explain why goodness-of-ﬁt tests are

not appropriate for binary data (Sect. 9.10).

9.2 Modelling Proportions

The outcome of many studies is a proportion y of a total number m:the

proportion of individuals having a disease; the proportion of voters who vote

in favour of a particular election candidate; the proportion of insects that die

after being exposed to diﬀerent doses of a poison. For all these examples, a

binomial distribution may be an appropriate response distribution. In each

case, the m individuals in each group are assumed to be independent, and

each individual can be classiﬁed into one of two possible outcomes.

The binomial distribution has already been established as an edm

(Example 5.3), and binomial glms used in examples in previous chapters to

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_9

333

334 9 Models for Proportions: Binomial GLMs

develop the theory of glms. Useful information about the binomial distribu-

tion appears in Table 5.1 (p. 221). The probability function for a binomial

edm is

P(y; μ, m)=





(1 − μ)

m(1−y)

(9.1)

where m is known and φ = 1, and where y =0, 1/m, 2/m,...1, and the

expected proportion is 0 <μ<1. To use the binomial distribution in a glm,

the prior weights w are set to the group totals m. The unit deviance for the

binomial distribution is

d(y, μ)=2



y log

+(1− y) log

1 − y

1 − μ



When y =0ory = 1, the limit form of the unit deviance (5.14) is used.

The residual deviance is D(y, ˆμ)=



i=1

d(y

, ˆμ

). By the saddlepoint

approximation, D(y, ˆμ) ∼ χ

n−p



for a model with p



parameters in the linear

predictor. The saddlepoint approximation is adequate if min{m

}≥3and

min{m

(1 − y

)}≥3 (Sect. 7.5).

A binomial glm is denoted glm(binomial; link), and is speciﬁed in r using

family=binomial() in the glm() call. Binomial responses may be speciﬁed

in the glm() formula in one of three ways:

1. The response can be supplied as the observed proportions y

, when the

sample sizes m

are supplied as the weights in the call to glm().

2. The response can be given as a two-column array, the columns giving the

numbers of successes and failures respectively in each group of size m

The prior weights weights do not need to be supplied (r computes the

weights m as the sum of the number of successes and failures for each

row).

3. The response can be given as a factor (when the ﬁrst factor level corre-

sponds to failures, and all others levels to successes) or as a logicals (ei-

ther TRUE, which is treated as the success, or FALSE). The prior weights

weights do not need to be supplied in this speciﬁcation (and are set to

one by default). This speciﬁcation is useful if the data have one row for

each observation (see Example 9.1). In this form, the responses are binary

and the model is a Bernoulli glm (see Example 4.6). While many of the

model statistics are the same (Problem 9.14), there are some limitations

with using this form (Sect. 9.10).

For binomial glms, the use of quantile residuals [5] is strongly recommended

for diagnostic analysis (Sect. 8.3.4.2).

Example 9.1. An experiment running turbines for various lengths of time [19,

20] recorded the proportion of turbine wheels y

out of a total of m

turbines

developing ﬁssures (narrow cracks) (Table 9.1; Fig. 9.1; data set: turbines).

A suitable model for the data may be a binomial glm.

9.2 Modelling Proportions 335

Tabl e 9. 1 The number of turbine wheels developing ﬁssures and the number of hours

they are run (Example 9.1)

Prop. of No. of Prop. of No. of

Case Hours Turbines ﬁssures ﬁssures Case Hours Turbines ﬁssures ﬁssures

1 400 39 0.0000 0 7 3000 42 0.2143 9

2 1000 53 0.0755 4 8 3400 13 0.4615 6

3 1400 33 0.0606 2 9 3800 34 0.6471 22

4 1800 73 0.0959 7 10 4200 40 0.5250 21

5 2200 30 0.1667 5 11 4600 36 0.5833 21

6 2600 39 0.2308 9

0 1000 2000 3000 4000 5000

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Hours of use

Proportion of turbines

with fissures

Fig. 9.1 The proportion of turbine wheels developing ﬁssures plotted against the num-

ber of hours of use. Larger plotting symbols indicate proportions based on larger sample

sizes. The numbers beside the points refer to the case number (Example 9.1)

For these data, the ﬁrst and second forms of specifying the response are

appropriate and equivalent:

> library(GLMsData); data(turbines)

> tur.m1 <- glm( Fissures/Turbines ~ Hours, family=binomial,

weights=Turbines, data=turbines)

> tur.m2 <- glm( cbind(Fissures, Turbines-Fissures) ~ Hours,

family=binomial, data=turbines)

> coef(tur.m1); coef(tur.m2)

(Intercept) Hours

-3.9235965551 0.0009992372

(Intercept) Hours

-3.9235965551 0.0009992372

To use the third form of data entry, the data would need to be rearranged

so that each individual turbine was represented in its own line, hence having



i=1

= 432 rows. 

336 9 Models for Proportions: Binomial GLMs

9.3 Link Functions

Speciﬁc link functions are required for binomial glms to ensure that 0 <

μ<1. Numerous suitable choices are available. Three link functions are

commonly used with the binomial distribution:

1. The logit (or logistic) link function, which is the canonical link function

for the binomial distribution and the default link function in r:

η = log

1 − μ

= logit(μ). (9.2)

(r uses natural logarithms.) This link function is speciﬁed in r using

link="logit". A binomial glm with a logit link function is often called

a logistic regression model.

2. The probit link function: η = Φ

−1

(μ) = probit(μ), where Φ(·)isthe

cdf for the normal distribution. This link function is speciﬁed in r as

link="probit".

3. The complementary log-log link function: η = log{−log(1−μ)}. This link

function is speciﬁed in r as link="cloglog".

In practice, the logit and probit link functions are very similar (Fig. 9.2). In

addition, both are symmetric about μ =0.5, whereas the complementary

log-log link function is not.

Two other less common link functions permitted in r for binomial glms

are the "cauchit" and "log" links. The "cauchit" link function is based

on the Cauchy distribution (see Sect. 9.4), but is rarely used in practice. The

−4 −2 0 2 4

0.0

0.2

0.4

0.6

0.8

1.0

The linear predictor η

The expected proportion μ

Logistic

Probit

Comp. log−log

Fig. 9.2 Common link functions used with the binomial distribution: the logit, probit,

and complementary log-log link functions (Sect. 9.3)

9.3 Link Functions 337

0246810

0.0

0.2

0.4

0.6

0.8

1.0

The expected proportion, μ

η=−5 + x

η=−5 + 2x

0246810

0.0

0.2

0.4

0.6

0.8

1.0

The expected proportion, μ

η=5 − x

η=5 − 2x

Fig. 9.3 The relationships between x and the predicted proportions μ for various linear

predictors η using the logit link function, where logit(μ)=η (Sect. 9.3)

"log" link function is sometimes used for modelling risk ratios or relative

risks. It is an approximation to the logit link when μ is small [16].

To understand the relationship between the explanatory variables and μ,

consider the case of one explanatory variable where η = β

+ β

x. Figure 9.3

shows the corresponding relationships between x and μ using the logit link

function.

Example 9.2. For the turbine data (data set: turbines), we can ﬁt binomial

glms using the three common link functions, using the hours run-time as the

explanatory variable:

> tr.logit <- glm( Fissures/Turbines ~ Hours, data=turbines,

family=binomial, weights=Turbines)

> tr.probit <- update( tr.logit, family=binomial(link="probit") )

> tr.cll <- update( tr.logit, family=binomial(link="cloglog") )

> tr.array <- rbind( coef(tr.logit), coef(tr.probit), coef(tr.cll))

> tr.array <- cbind( tr.array, c(deviance(tr.logit),

deviance(tr.probit), deviance(tr.cll)) )

> colnames(tr.array) <- c("Intercept", "Hours","Residual dev.")

> rownames(tr.array) <- c("Logit","Probit","Comp log-log")

> tr.array

Intercept Hours Residual dev.

Logit -3.923597 0.0009992372 10.331466

Probit -2.275807 0.0005783211 9.814837

Comp log-log -3.603280 0.0008104936 12.227914

The residual deviances are similar for the logit and probit glms, and slightly

larger for the complementary log-log link function. The coeﬃcients from the

three models are reasonably diﬀerent. However, the models themselves are

very similar, as we can see by plotting the models. To do so, ﬁrst set up a

vector of values for the run-time:

> newHrs <- seq( 0, 5000, length=100)

338 9 Models for Proportions: Binomial GLMs

0 1000 2000 3000 4000 5000

0.0

0.1

0.2

0.3

0.4

0.5

0.6

0.7

Hours run

Proportion with fissures

Logit

Probit

Comp. log−log

Fig. 9.4 The turbines data, showing the ﬁtted binomial glms, using logistic, probit

and complementary log-log link functions (Example 9.2)

Now, make predictions from these values using each model:

> newdf <- data.frame(Hours=newHrs)

> newP.logit <- predict( tr.logit, newdata=newdf, type="response")

> newP.probit <- predict( tr.probit, newdata=newdf, type="response")

> newP.cll <- predict( tr.cll, newdata=newdf, type="response")

The type of prediction is set as "response" because, by default, predict()

returns the predictions on the linear predictor scale (that is, ˆη is returned

rather than ˆμ). Now, plot these predictions using lines(), then add a legend

(Fig. 9.4):

> plot( Fissures/Turbines ~ Hours, data=turbines, pch=19, las=1,

xlim=c(0, 5000), ylim=c(0, 0.7),

xlab="Hours run", ylab="Proportion with fissures")

> lines( newP.logit ~ newHrs, lty=1, lwd=2)

> lines( newP.probit ~ newHrs, lty=2, lwd=2)

> lines( newP.cll ~ newHrs, lty=4, lwd=2)

> legend("topleft", lwd=2, lty=c(1, 2, 4),

legend=c("Logit","Probit","Comp. log-log"))

All three models produce similar predictions, which is not unusual. 

9.4 Tolerance Distributions and the Probit Link

The link functions can be understood using a threshold interpretation. In

what follows, we show how the threshold interpretation applies for the probit

link function, using the turbines data as the example.

Assume each individual turbine has a diﬀerent tolerance beyond which

it will develop ﬁssures. As part of the natural variation in turbines, this

9.4 Tolerance Distributions and the Probit Link 339

tolerance varies from turbine to turbine (but is ﬁxed for any one turbine).

Denote this tolerance level as t

for turbine i; note that t

is a continuous

variable. Assume that t

follows a normal distribution with mean tolerance

,sothat



∼ N(τ

,σ

)

= β



+ β



(9.3)

where x

is the number of hours that turbine i is run. In this context, the

normal distribution in (9.3) is called the tolerance distribution.

The variable of interest is whether or not the turbines develop ﬁssures.

Assume that turbines develop ﬁssures if the tolerance level t

of turbine i is

less than some ﬁxed tolerance threshold T . In other words, deﬁne



1ift

≤ T , and the turbine develops ﬁssures

0ift

>T, and the turbine does not develop ﬁssures.

Then, the probability that turbine i develops ﬁssures is

=Pr(y

=1)=Pr(t

≤ T )=Φ



T − τ



, (9.4)

where Φ(·)isthecdf of the standard normal distribution. We can write

T − τ

T − β



− β



= β

+ β

with β

=(T − β



)/σ and β

= −β



/σ. Then (9.4) becomes

g(μ

)=β

+ β

where g() is the probit link function.

Other choices of the tolerance distribution lead to other link functions

by a similar process (Table 9.2). The logit link function emerges as the link

function when the logistic distribution is used as the tolerance distribution

(Problem 9.4). The complementary log-log link function emerges as the link

function when the extreme value (or Gumbel) distribution is used as the

tolerance distribution. The cauchit link function assumes the threshold dis-

tribution is the Cauchy distribution. The logistic and normal tolerance dis-

tributions are both symmetric, and usually give similar results except for

probabilities near zero or one. In contrast, the extreme value distribution is

not symmetric, so the complementary log-log link function often gives some-

what diﬀerent results than using the logit and probit link functions (Fig. 9.2).

In principle, the cdf for any continuous distribution can be used as a basis

for the link function.

340 9 Models for Proportions: Binomial GLMs

Tabl e 9 . 2 Tolerance distributions leading to link functions for binomial glms(Sect.9.3)

Link function Tolerance distribution Distribution function

Logit Logistic F(y)=exp(y)/ {1+exp(y)}

Probit Normal F(y)=Φ(y)

Complementary log-log Extreme value F(y)=1− exp {−exp(y)}

Cauchit Cauchy F(y)={arctan(y)+0.5}/π

9.5 Odds, Odds Ratios and the Logit Link

Using the logit link function with the binomial distribution produces a useful

interpretation. To understand this interpretation, the concept of odds ﬁrst

must be understood. If event A has probability μ of occurring, then the odds

of event A occurring is the ratio of the probability that A occurs to the

probability that A does not occur: μ/(1 −μ). For example, if the probability

that a turbine develops ﬁssures is 0.6, the odds that a turbine develops ﬁssures

is 0.6/(1 − 0.6) = 1.5. This means that the probability of observing ﬁssures

is 1.5 times greater than the probability of not observing a ﬁssure (that is,

1.5 × 0.4=0.6). Clearly, using the logit link function in a binomial glm is

equivalent to modelling the logarithm of the odds (or the ‘log-odds’).

The binomial glm using the logit function can be written as

log(odds) = β

+ β

or equivalently odds = exp(β

){exp(β

)}

As x increases by one unit, the log-odds increase by linearly by an amount

. Alternatively, if x increases by one unit, the odds increase by a factor of

exp(β

). These interpretations in terms of the odds have intuitive appeal, and

for this reason the logit link function is often preferred for the link function.

Example 9.3. For the turbines data (data set: turbines), the ﬁtted logistic

regression model (Example 9.1) has coeﬃcients:

> coef(tr.logit)

(Intercept) Hours

-3.9235965551 0.0009992372

In this model, increasing Hours by one increases the odds of a turbine de-

veloping ﬁssures by exp(0.0009992) = 1.001. In this case, the interpretation

is more useful if we consider increasing Hours by 1000 h. This increases the

odds of a turbine developing ﬁssures by exp(1000×0.0009992) = 2.716 times.

Using the logistic regression model tr.logit assumes that the relationship

between the run-time and the log-odds is approximately linear (Fig. 9.5):

9.5 Odds, Odds Ratios and the Logit Link 341

0 1000 3000 5000

−5

−4

−3

−2

−1

Run−time (in hours)

Log−odds

0 1000 3000 5000

0.0

0.5

1.0

1.5

2.0

Run−time (in hours)

Odds

Fig. 9.5 The log-odds plotted against the run-time (left panel) and the odds plotted

against the run-time (right panel) for the binomial logistic glm ﬁtted to the turbine

data (Example 9.3)

> LogOdds <- predict( tr.logit ); odds <- exp( LogOdds )

> plot( LogOdds ~ turbines$Hours, type="l", las=1,

xlim=c(0, 5000), ylim=c(-5, 1),

ylab="Log-odds", xlab="Run-time (in hours)" )

> my <- turbines$Fissures; m <- turbines$Turbines

> EmpiricalOdds <- (my + 0.5)/(m - my + 0.5) # To avoid log of zeros

> points( log(EmpiricalOdds) ~ turbines$Hours)

> plot( odds ~ turbines$Hours, las=1, xlim=c(0, 5000), ylim=c(0, 2),

type="l", ylab="Odds", xlab="Run-time (in hours)")

> points( EmpiricalOdds ~ turbines$Hours)

Note the use of empirical log-odds, adding 0.5 to both the numerator and

denominator of the odds, so that the log-odds can be computed even when

y =0. 

Logistic regression models are often ﬁtted to data sets that include factors

as explanatory variables. In these situations, the concept of the odds ratio is

useful to deﬁne. Consider the binomial glm with systematic component

log

1 − μ

= log-odds = β

+ β

where x is a dummy variable taking the values 0 or 1. From this equation,

we see that the odds of observing a success when x = 0 is exp(β

), and the

odds of observing a success when x = 1 is exp(β

+ β

) = exp(β

)exp(β

The ratio of these two odds is exp(β

). This means that the odds of a success

occurring when x = 1 is exp(β

) times greater than when x = 0. This ratio is

called the odds ratio, often written or. When a number of factors are ﬁtted

as explanatory variables, each of the corresponding regression parameters β

can be interpreted as odds ratios in a similar manner.

342 9 Models for Proportions: Binomial GLMs

Tabl e 9. 3 The germination of two types of seeds for two root extracts. The number of

seeds germinating my from m seeds planted is shown (Table 9.4)

O. aegyptiaco 75 seeds O. aegyptiaco 73 seeds

Bean extracts Cucumber extracts Bean extracts Cucumber extracts

my m my m my m my m

10 39 5 6 8 16 3 12

23 62 53 74 10 30 22 41

23 81 55 72 8 28 15 30

26 51 32 51 23 45 32 51

17 39 46 79 0 4 3 7

10 13

Bean Cucumber

0.0

0.2

0.4

0.6

0.8

1.0

Extract

Germ/Total

OA73 OA75

0.0

0.2

0.4

0.6

0.8

1.0

Seeds

Germ/Total

Fig. 9.6 The germination data: germination proportions plotted against extract type

(left panel) and seed type (right panel) (Example 9.4)

Example 9.4. A study [3] of seed germination used two types of seeds and two

typesofrootstocks(Table9.3; data set: germ). A plot of the data (Fig. 9.6)

shows possible relationships between the proportions of seeds germinating

and both factors:

> data(germ); str(germ)

'data.frame': 21 obs. of 4 variables:

$ Germ : int 10 23 23 26 17 5 53 55 32 46 ...

$ Total : int 39 62 81 51 39 6 74 72 51 79 ...

$ Extract: Factor w/ 2 levels "Bean","Cucumber": 1111122222...

$ Seeds : Factor w/ 2 levels "OA73","OA75": 2222222222...

> plot( Germ/Total ~ Extract, data=germ, las=1, ylim=c(0, 1) )

> plot( Germ/Total ~ Seeds, data=germ, las=1, ylim=c(0, 1) )

The model with both factors as explanatory variables can be ﬁtted:

> gm.m1 <- glm(Germ/Total ~ Seeds + Extract, family=binomial,

data=germ, weights=Total)

> printCoefmat(coef(summary(gm.m1)))

9.6 Median Eﬀective Dose, ED50 343

Estimate Std. Error z value Pr(>|z|)

(Intercept) -0.70048 0.15072 -4.6475 3.359e-06 ***

SeedsOA75 0.27045 0.15471 1.7482 0.08044 .

ExtractCucumber 1.06475 0.14421 7.3831 1.546e-13 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Recall the r output means that the r variable Seeds takes the value one for

OA75 and is zero for OA73. Likewise the r variable Extract takes the value

one for Cucumber and is zero for Bean.

Note that

> exp( coef(gm.m1) )

(Intercept) SeedsOA75 ExtractCucumber

0.4963454 1.3105554 2.9001133

This means that the odds of seed germination occurring using cucumber

extracts is 2.900 times the odds of seed germination occurring using bean

extracts. Similarly, the odds of seed germination occurring using O. aegypti-

aco 75 seeds are 1.311 times the odds of seed germination occurring using O.

aegyptiaco 73 seeds.

These data are explored later also (Example 9.8), where the interaction

term is considered. 

9.6 Median Eﬀective Dose, ED50

Binomial glms are commonly used to examine the relationship between the

dose d of a drug or poison and the proportion y of insects (or plants, or

animals) that survive. These models are called dose–response models. Asso-

ciated with these experiments is the concept of the median eﬀective dose,

ed50: the dose of poison aﬀecting 50% of the insects. Diﬀerent ﬁelds use dif-

ferent names for similar concepts, such as median lethal dose ld50 or median

lethal concentration lc50. Here, for simplicity, we use ed50 to refer to any

of these quantities. The ed50 concept can be applied to other contexts also.

By deﬁnition, μ =0.5attheed50.

For a binomial glm using a logit link function, η = logit(μ) = 0 when

μ =0.5. Writing the linear predictor as η = β

+ β

d where d is the dose,

then solving for the dose d shows that ed50 = −

. More generally,

the dose eﬀective on any proportion ρ of the population, denoted ed(ρ), is

estimated by

ed(ρ)=

g(ρ) − β

where g() refers to the link function used in ﬁtting the model. In Problem 9.2,

formulae are developed for computing ed50 for the probit and complementary

log-log link functions.

344 9 Models for Proportions: Binomial GLMs

The function dose.p() in the r package MASS (which comes with r

distributions) conveniently returns



ed(ρ) and the corresponding estimated

standard error. The ﬁrst input to dose.p() is the glm() object, and the

second input identiﬁes the two coeﬃcients of importance: the coeﬃcient for

the intercept and for the dose (in that order). By default, these are assumed

to be the ﬁrst and second coeﬃcients. The third input is ρ; by default ρ =0.5,

and so



ed50 is returned by default.

Example 9.5. Consider the turbine data again (data set: turbines). The ed50

corresponds to the run time for which 50% of turbines would be expected to

experience ﬁssures:

> library(MASS) # MASS comes with R

> ED50s <- cbind("Logit" = dose.p(tr.logit),

"Probit" = dose.p(tr.probit),

"C-log-log" = dose.p(tr.cll))

> ED50s

Logit Probit C-log-log

p = 0.5: 3926.592 3935.197 3993.575

Running the turbines for approximately 3927 h would produce ﬁssures in

about 50% of the turbines (using the logistic link function model). All three

link functions produce similar estimates of ed50, which seems reasonable

based on Fig. 9.4 (p. 338). 

9.7 The Complementary Log-Log Link in Assay Analysis

A common problem in biology is to determine the proportion of cells or

organisms of interest amongst a much larger population. For example, does

a sample of tissue contain infective bacteria, and how many? Or what is the

frequency of adult stem cells in a sample of tissue?

Suppose the presence of active particles can be detected by undertaking an

assay. For example, the presence of bacteria might be detected by incubating

the sample on an agar plate, and observing whether a bacterial culture grows.

Or the presence of stem cells might be detected by transplanting cells into a

host animal, and observing whether a new growth occurs. However, the same

response is observed, more or less, regardless of the number of active particles

in the original sample. A single stem cell would result in a new growth. When

a growth is observed, we cannot determine directly whether there was one

stem cell or many to start with.

Dilution assays are an experimental technique to estimate the frequency

of active cells. The idea is to dilute the sample down to the point where some

assays yield a positive result (so at least one active particles is present) and

some yield a negative result (so no active particles are present).

The fundamental property of limiting dilution assays is that each assay

results in a positive or negative result. Write μ

for the probability of a

9.7 The Complementary Log-Log Link in Assay Analysis 345

positive result given that the expected number of cells in the culture is d

If m

independent cultures are conducted at dose d

, then the number of

positive results follows a binomial distribution.

Write λ for the proportion of active cells in the cell population, so that

the expected number of active cells in the culture is λd

. If the cells behave

independently (that is, if there are no community eﬀects amongst the cells),

and if the cell dose is controlled simply by dilution, then the actual number of

cells in each culture will vary according to a Poisson distribution. A culture

will give a negative result only if there are no active cells in the assay. The

Poisson probability formula tells us that this occurs with probability

1 − μ

=exp(−λd

This formula can be linearized by taking logarithms of both sides, as

log(1 − μ

)=−λd

(9.5)

or, taking logarithms again,

log{−log(1 − μ

)} = log λ + log d

. (9.6)

This last formula is the famous complementary log-log transformation from

Mather [18].

The proportion of active cells can be estimated by ﬁtting a binomial glm

with a complementary log-log link:

g(μ

)=β

+ log d

(9.7)

where log d

is an oﬀset and g() is the complementary log-log link function.

The estimated proportion of active cells is then

λ =exp(

In principle, a glm could also have be ﬁtted using (9.5) as a link-linear

predictor, in this case with a log-link. However (9.6) is superior, because it

leads to a glm (9.7) without any constraints on the coeﬃcient β

As usual, a conﬁdence interval is given by

± z

α/2

se(

)

where se(

) is the standard error of the estimate and z

α/2

is the critical

value of the normal distribution, e.g., z =1.96 for a 95% conﬁdence interval.

To get back to the active cell frequency simply exponentiate and invert the

estimate and the conﬁdence interval: 1/

λ =exp(−

). Conﬁdence intervals

can be computed for 1/λ, representing the number of cells required on average

to obtain one responding cell.

The dilution assay model assumes that a single active cell is suﬃcient

to achieve a positive result, so it is sometimes called the single-hit model

(though other assumptions are possible [25]). One way to check this model is

346 9 Models for Proportions: Binomial GLMs

Tabl e 9 .4 The average number of cells in each assay in which cells were transplanted

in host mice, the number of assays at that cell number, and the number of assays giving

a positive outcome, a milk gland outgrowth (Example 9.6)

Number of cells Number of Number of

per assay assays outgrowths

15 38 3

40 6 6

60 17 13

90 8 6

125 12 9

to ﬁt a slightly larger model in which the oﬀset coeﬃcient is not set to one:

g(μ

)=β

+ β

log d

The correctness of the single-hit model can then be checked [10] by testing

the null hypothesis H

: β

=1.

Example 9.6. Shackleton et al. [21] demonstrated the existence of adult mam-

mary stem cells. They showed, for the ﬁrst time, that a complete mammary

milk producing gland could be produced in mice from a single cell. After a

series of steps, they were able to purify a population of cells that was highly

enriched for mammary stem cells, although stem cells were still a minority

of the total.

The data (Table 9.4; data set: mammary) relate to a number of assays in

which cells were transplanted into host mice. A positive outcome here consists

of seeing a milk gland outgrowth, evidence that the sample of cells included

as least one stem cell. The data give the average number of cells in each assay,

the number of assays at that cell number, and the number of assays giving a

positive outcome.

> data(mammary); mammary

N.Cells N.Assays N.Outgrowths

115 38 3

240 6 6

360 17 13

490 8 6

5 125 12 9

> y <- mammary$N.Outgrowths / mammary$N.Assays

> fit <- glm(y~offset(log(N.Cells)), family=binomial(link="cloglog"),

weights=N.Assays, data=mammary)

> coef(summary(fit))

Estimate Std. Error z value Pr(>|z|)

(Intercept) -4.163625 0.1744346 -23.86925 6.391454e-126

> frequency <- 1/exp(coef(fit)); frequency

(Intercept)

64.30418

9.8 Overdispersion 347

The mammary stem cell frequency is estimated to be about 1 in 64 cells. A

95% conﬁdence interval is computed as follows:

> s <- summary(fit)

> Estimate <- s$coef[, "Estimate"]

> SE <- s$coef[, "Std. Error"]

> z <- qnorm(0.05/2, lower.tail=FALSE)

> CI <- c(Lower=Estimate+z*SE, Estimate=Estimate, Upper=Estimate-z*SE)

> CI <- 1/exp(CI); round(CI, digits=1)

Lower Estimate Upper

45.7 64.3 90.5

The frequency of stem cells is between 1/46 and 1/91. There is no evidence

of any deviation from the single-hit model:

> fit1 <- glm(y~log(N.Cells), family=binomial(link="cloglog"),

weights=N.Assays, data=mammary)

> anova(fit, fit1, test="Chisq")

Analysis of Deviance Table

Model 1: y ~ offset(log(N.Cells))

Model 2: y ~ log(N.Cells)

Resid. Df Resid. Dev Df Deviance Pr(>Chi)

1 4 16.852

2 3 16.205 1 0.6468 0.4213



9.8 Overdispersion

For a binomial distribution, var[y]=μ(1 − μ). However, in practice the

amount of variation in the data can exceed μ(1 − μ), even for ostensibly

binomial-like data. This is called overdispersion. Underdispersion also occurs,

but is less common.

Overdispersion has serious consequences for the glm. It means that stan-

dard errors returned by the glm are underestimated, and tests on the ex-

planatory variables will generally appear to be more signiﬁcant that war-

ranted by the data, leading to overly complex models.

Overdispersion is detected by conducting a goodness-of-ﬁt test, as de-

scribed in Sect. 7.4. If the residual deviance and Pearson statistics are much

greater than the residual degrees of freedom, then there is evidence of lack of

ﬁt. Lack of ﬁt may be caused by an inadequate model, for example because

important explanatory variables are missing from the model. However, if all

relevant or possible explanatory variables are already included in the model,

and the data has been checked for outliers that might inﬂate the residuals,

but lack of ﬁt remains, then overdispersion is the alternative interpretation.

Overdispersion means that the binomial model is incorrect in some re-

spect. Overdispersion can arise from two major causes. The probabilities μ

348 9 Models for Proportions: Binomial GLMs

are not constant between observations, even when all the explanatory vari-

ables are unchanged. Alternatively the m

cases, of which observation y

is a

proportion, are not independent.

The ﬁrst type of overdispersion can be modelled by a hierarchical model.

Suppose that m

follows a binomial distribution with m

cases and success

probability p

. Suppose that the p

is itself a random variable, with mean μ

Then

E[y

]=μ

but

var[y

] >μ

(1 − μ

)/m

The greater the variability of p

the greater the degree of overdispersion. A

commonly-used model is to assume that p

follows a beta distribution [3].

This leads to a beta-binomial model for y

in which

var[y

]=φ

(1 − μ

)/m

, (9.8)

where φ

depends on m

and the parameters of the beta distribution.

More generally, overdispersion arises when the m

Bernoulli cases, that

make up observation y

, are positively correlated. For example, positive cases

may arrive in clusters rather than as individual cases. Writing ρ for the cor-

relation between the Bernoulli trials leads to the same variance as the beta-

binomial model (9.8) with φ

=1+(m

− 1)ρ.Ifthem

are approximately

equal, or if ρ is inversely proportional to m

−1, then the φ

will be approx-

imately equal. In this case, both overdispersion models lead to variances

var[y

]=φμ

(1 − μ

)/m

which are larger but proportional to the variances under the binomial model.

Note that overdispersion cannot arise for binary data with m

=1.

This reasoning leads to the idea of quasi-binomial models (Sect. 8.10).

Quasi-binomial models keep the same variance function V (μ)=μ(1 − μ)as

binomial glms, but allow a general positive dispersion φ instead of assuming

φ = 1. The dispersion parameter is usually estimated by the Pearson estima-

tor (Sect. 6.8.5). Quasi-binomial models do not correspond to any edm, but

the quasi-likelihood theory of Sect. 8.10 provides reassurance that the model

will still yield consistent estimators provided that the variance function rep-

resents the correct mean–variance relationship. In particular, quasi-binomial

models will give consistent estimators of the model coeﬃcients under the

beta-binomial or correlation models described above when the m

are roughly

equal. Even when the m

are not equal, a quasi-binomial model is likely still

preferable to assuming φ = 1 when overdisperion is present.

9.8 Overdispersion 349

The parameter estimates for binomial and quasi-binomial glms are iden-

tical (since the estimates

do not depend on φ), but the standard errors

are diﬀerent. The eﬀect of using the quasi-binomial model is to inﬂate the

standard error of the parameter estimates by

√

φ, so conﬁdence intervals and

statistics for testing hypotheses tests will change.

A quasi-binomial model is ﬁtted in r using glm() by using family=

quasibinomial().Asforfamily=binomial(), the default link function

for the quasibinomial() family is the "logit" link, while "probit",

"cloglog", "cauchit",and"log" are also permitted. Since the quasi-

binomial model is not based on a probability model, the aic is undeﬁned.

Example 9.7. Machine turbines operate more or less independently, so it

seems reasonable to suppose that independence between Bernoulli trials

might hold for the turbines data (data set: turbines). Indeed neither the

residual deviance nor the Pearson statistics show any evidence of overdisper-

sion (using model tr.logit ﬁtted in Example 9.1):

> c(Df = df.residual( tr.logit ),

Resid.Dev = deviance( tr.logit ),

Pearson.X2 = sum( resid(tr.logit, type="pearson")^2 ))

Df Resid.Dev Pearson.X2

9.000000 10.331466 9.250839

Neither goodness-of-ﬁt statistic is appreciably larger than the residual degrees

of freedom. This data set does contain two small values of m

, but these are

too few to change the conclusion even if the residuals for these observations

were underestimated. 

Example 9.8. Example 9.4 (p. 341) discussed the seed germination for two

types of seeds and two types of root stocks (data set: germ). Since seeds

are usually planted together in common plots, it is highly possible that they

might interact or be aﬀected by common causes; in other words we might

well expect seeds to be positively correlated, leading to overdispersion. We

start by ﬁtting a binomial glm with Extract and Seed and their interaction

as explanatory variables:

> gm.m1 <- glm( Germ/Total ~ Extract * Seeds, family=binomial,

weights=Total, data=germ )

> anova(gm.m1, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 20 98.719

Extract 1 55.969 19 42.751 7.364e-14 ***

Seeds 1 3.065 18 39.686 0.08000 .

Extract:Seeds 1 6.408 17 33.278 0.01136 *

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

> df.residual(gm.m1)

[1] 17

350 9 Models for Proportions: Binomial GLMs

−2 −1 0 1 2

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

0.40 0.50 0.60

−2

−1

Residuals vs fitted

Fitted value

Quantile residual

Fig. 9.7 Diagnostic plots after ﬁtting a binomial glm to the seed germination data

(Example 9.8)

Despite the fact that the maximal possible explanatory model has been ﬁtted,

overdispersion is clearly present; the residual deviance is much larger than

the residual degrees of freedom:

> c( deviance(gm.m1), df.residual(gm.m1) )

[1] 33.27779 17.00000

The Pearson statistic tells the same story:

> sum( resid(gm.m1, type="pearson")^2 ) # Pearson.X2

[1] 31.65114

There are no large residuals present that would suggest outliers (Fig. 9.7):

> library(statmod)

> qres <- qresid(gm.m1); qqnorm(qres, las=1); abline(0, 1)

> scatter.smooth( qres~fitted(gm.m1), las=1, main="Residuals vs fitted",

xlab="Fitted value", ylab="Quantile residual")

The chi-square approximation to the goodness-of-ﬁt statistics seems good

enough. The data includes one observation (number 16) with my =0and

other with m − my = 1 (number 6), but neither has a large enough residual

to be responsible for the apparent overdispersion:

> qres[c(6, 16)]

[1] 1.180272 -1.172095

Finally, this a designed experiment, with nearly equal numbers of obser-

vations in each combination of the experimental factors Extract and Seeds,

so inﬂuential observations cannot be an issue.

9.9 When Wald Tests Fail 351

Having ruled out all alternative explanations, we accept that overdisper-

sion is present and ﬁt a quasi-binomial model:

> gm.od <- update(gm.m1, family=quasibinomial)

> anova(gm.od, test="F")

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 20 98.719

Extract 1 55.969 19 42.751 30.0610 4.043e-05 ***

Seeds 1 3.065 18 39.686 1.6462 0.21669

Extract:Seeds 1 6.408 17 33.278 3.4418 0.08099 .

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Note that F -tests are used for comparisons between quasi-binomial models.

This follows because the dispersion φ is estimated (using the Pearson es-

timator by default). The quasi-binomial analysis of deviance suggests that

only Extract is signiﬁcant in the model, so germination frequency diﬀers by

root stock but not by seed type, unlike the binomial glm which showed a

signiﬁcant Extract by Seeds interaction.

The binomial and quasi-binomial glms give identical coeﬃcient estimates,

but the standard errors from the quasi-binomial glm are

√

φ times those from

the binomial model:

> sqrt(summary(gm.od)$dispersion)

[1] 1.36449

> beta <- coef(summary(gm.m1))[,"Estimate"]

> m1.se <- coef(summary(gm.m1))[,"Std. Error"]

> od.se <- coef(summary(gm.od))[,"Std. Error"]

> data.frame(Estimate=beta, Binom.SE=m1.se,

Quasi.SE=od.se, Ratio=od.se/m1.se)

Estimate Binom.SE Quasi.SE Ratio

(Intercept) -0.4122448 0.1841784 0.2513095 1.36449

ExtractCucumber 0.5400782 0.2498130 0.3408672 1.36449

SeedsOA75 -0.1459269 0.2231659 0.3045076 1.36449

ExtractCucumber:SeedsOA75 0.7781037 0.3064332 0.4181249 1.36449



9.9 When Wald Tests Fail

Standard errors and Wald tests experience special diﬃculties when the ﬁtted

values from binomial glms are very close to zero or one. When the linear

predictor includes factors, sometimes in practice there is a factor level for

which the y

are either all zero or all one. In this situation, the ﬁtted values

estimated by the model will also be zero or one for this level of the factor.

This situation inevitably causes problems for standard errors and Wald tests,

because at least one of the coeﬃcients in the linear predictor must tend to

inﬁnity as the ﬁtted model converges.

352 9 Models for Proportions: Binomial GLMs

Suppose for example that the logit link function is used, so the ﬁtted values

are related to the linear predictor by

ˆμ =

exp(ˆη)

1 + exp(ˆη)

. (9.9)

Suppose also that the model includes just one explanatory variable x,so

η = β

+ β

x. The only way for ˆμ to be zero or one is for ˆη to be ±∞.If

ˆμ → 0, then ˆη →−∞, which implies

→−∞and/or

x →−∞. In other

words, one or both of the parameters must approach ±∞.Ifˆμ → 1, then

ˆη →∞and a similar situation exists. The phenomenon is the same for other

link functions.

When parameter estimates approach ±∞, the standard errors for those

parameters must also approach ±∞, and Wald test statistics, which are ratios

of coeﬃcients to standard errors (Sect. 7.2.1), become very unreliable [23,

p. 197]. In particular, the standard errors often tend to inﬁnity faster than

the coeﬃcients themselves, meaning that the Wald statistic tends to zero,

regardless of the true signiﬁcance of the variable. This is called the Hauck–

Donner eﬀect [7].

Despite the problems with Wald tests, the likelihood ratio and score test

usually remain quite serviceable in these situations, even when ﬁtted values

are zero or one. This is because the problem of inﬁnite parameters is remov-

able, in principle, by re-parametrising the model, and likelihood ratio and

score tests are invariant to reparameterization. Wald tests are very suscep-

tible to inﬁnite parameters in the model because they are dependent on the

particular parameterization used.

Example 9.9. A study [17] of the habitats of the noisy miner (a small but

aggressive native Australian bird) recorded whether noisy miners were de-

tected in various two hectare transects in buloke woodland patches (data set:

nminer). Part of this data frame was discussed in Example 1.5 (p. 14), where

models were ﬁtted for the number of noisy miners.

Here we consider ﬁtting a binomial glm to model the presence of noisy

miners in each buloke woodland patch (Miners). More speciﬁcally, we study

whether the presence of noisy miners is impacted by whether or not the

number of eucalypts exceeds 15 or not:

> data(nminer); Eucs15 <- nminer$Eucs>15

> m1 <- glm(Miners ~ Eucs15, data=nminer, family=binomial)

> printCoefmat(coef(summary(m1)))

Estimate Std. Error z value Pr(>|z|)

(Intercept) -0.84730 0.48795 -1.7364 0.08249 .

Eucs15TRUE 20.41337 3242.45694 0.0063 0.99498

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

9.9 When Wald Tests Fail 353

The Wald test results indicate that the explanatory variable is not signiﬁ-

cant: P =0.995. Note the large standard error for Eucs15. Compare to the

likelihood ratio test results:

> anova(m1, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 30 42.684

Eucs15 1 18.25 29 24.435 1.937e-05 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The likelihood ratio test results indicate that the explanatory variable is

highly signiﬁcant: P ≈ 0. Similarly, the score test results indicate that Miners

is highly signiﬁcant also:

> m0 <- glm(Miners ~ 1, data=nminer, family=binomial)

> z.score <- glm.scoretest(m0, Eucs15)

> P.score <- 2*(1-pnorm(abs(z.score))); c(z.score, P.score)

[1] 3.7471727820 0.0001788389

Despite the Wald test results, a plot of Miners against Eucs15 (Fig. 9.8)

shows an obvious relationship: in woodland patches with more than 15 euca-

lypts, noisy miners were always observed:

> plot( factor(Miners, labels=c("No","Yes")) ~ factor(Eucs15), las=1,

ylab="Noisy miners present?", xlab="Eucalypts > 15", data=nminer)

> plot( Miners ~ Eucs, pch=ifelse(Eucs15, 1, 19), data=nminer, las=1)

> abline(v=15.5, col="gray")

The situation is exactly as described in the text, and an example of the

Hauck–Donner eﬀect. This means that the Wald test results are not trust-

worthy. When the number of eucalypts exceeds 15, all woodland patches in

the sample have noisy miners, so ˆμ → 1. This is achieved as

→∞.The

ﬁtted probability when Eucs15 is TRUE is one to computer precision:

Eucalypts > 15

Noisy miners present?

FALSE TRUE

Yes

0.0 0.2 0.4 0.6 0.8 1.0

l l

llll

lll

llll l ll l

lll

0 5 10 15 20 25 30

0.0

0.2

0.4

0.6

0.8

1.0

Eucs

Miners

Fig. 9.8 The presence of noisy miners. Left panel: the presence of noisy miners as a

function of whether 15 eucalypts are observed or not; right panel: the presence of noisy

miners as a function of the number of eucalypts, showing the division at 15 eucalypts

(Example 9.9)

354 9 Models for Proportions: Binomial GLMs

> tapply(fitted(m1), Eucs15, mean)

FALSE TRUE

0.3 1.0

In this situation, the score or likelihood ratio tests must be used instead of

the Wald test. 

9.10 No Goodness-of-Fit for Binary Responses

When m

= 1 for all i, the binomial responses y

are all 0 or 1; that is, the

data are binary. In this case the residual deviance and Pearson goodness-of-

ﬁt statistics are determined entirely by the ﬁtted values. This means that

there is no concept of residual variability, and goodness-of-ﬁt tests are not

meaningful. For binary data, likelihood ratio tests and score tests should be

used, making sure that p



is much smaller than n.

Example 9.10. In the nminer example in the previous section, the residual

deviance is less than the residual degrees of freedom. This might be thought

to suggest underdispersion, but it has no meaning. The size of the residual

deviance is determined only by the sizes of the ﬁtted values, and how far they

are from zero and one. 

9.11 Case Study

An experiment [8, 13] exposed batches of insects to various deposits (in mg) of

insecticides (Table 9.5; data set: deposit). The proportion of insects y killed

after six days of exposure in each batch of size m is potentially a function of

the dose of insecticide and the type of insecticide. The data are available in

the r package GLMsData:

Tabl e 9 .5 The number of insects killed z

= y

out of a total of m

insects, after

three days exposure to diﬀerent deposits of insecticides (Sect. 9.11)

Amount of deposit (in mg)

2.00 2.64 3.48 4.59 6.06 8.00

Insecticide z

A 350 549 1947 1938 2429 3550

B 2 50 14 49 20 50 27 50 41 50 40 50

C 2850 3750 4650 4850 4850 5050

9.11 Case Study 355

2345678

0.0

0.2

0.4

0.6

0.8

1.0

Proportion of

insects killed

Deposit (in mg)

Proportion killed

0.2 0.4 0.6 0.8 1.0

−3

−2

−1

Quantile resids. plotted

against fitted values

Fitted values

Residuals

2345678

−3

−2

−1

Logits plotted

against Deposit

Deposit

LogOdds

Insecticide A

Insecticide B

Insecticide C

Fig. 9.9 The insecticide data. Top left panel: the data, showing the ﬁtted model ins.m1;

top right panel: a plot of the quantile residuals against the ﬁtted values; bottom panel:

the log-odds plotted against the deposit (Sect. 9.11)

> data(deposit); str(deposit)

'data.frame': 18 obs. of 4 variables:

$ Killed : int 3 5 19 19 24 35 2 14 20 27 ...

$ Number : int 50 49 47 38 29 50 50 49 50 50 ...

$ Insecticide: Factor w/ 3 levels "A","B","C": 1111112222...

$ Deposit : num 2 2.64 3.48 4.59 6.06 8 2 2.64 3.48 4.59 ...

A plot of the data (Fig. 9.9,p.355, top left panel) shows insecticides A

and B appear to have similar eﬀects, while insecticide C appears diﬀerent

from A and B. The amount of deposit clearly is signiﬁcant:

> deposit$Prop <- deposit$Killed / deposit$Number

> plot( Prop ~ Deposit, type="n", las=1, ylim=c(0, 1),

data=deposit, main="Proportion of\ninsects killed",

xlab="Deposit (in mg)", ylab="Proportion killed")

> points( Prop ~ Deposit, pch="A", subset=(Insecticide=="A"), data=deposit)

> points( Prop ~ Deposit, pch="B", subset=(Insecticide=="B"), data=deposit)

> points( Prop ~ Deposit, pch="C", subset=(Insecticide=="C"), data=deposit)

356 9 Models for Proportions: Binomial GLMs

A model using the deposit amount and the type of insecticide as explanatory

variables seems sensible:

> ins.m1 <- glm(Killed/Number ~ Deposit + Insecticide,

family = binomial, weights = Number, data = deposit)

> coef(ins.m1)

(Intercept) Deposit InsecticideB InsecticideC

-3.2213638 0.6316762 0.3695267 2.6880162

The ﬁtted lines are shown in the top left panel of Fig. 9.9:

> newD <- seq( min(deposit$Deposit), max(deposit$Deposit), length=100)

> newProp.logA <- predict(ins.m1, type="response",

newdata=data.frame(Deposit=newD, Insecticide="A") )

> newProp.logB <- predict(ins.m1, type="response",

newdata=data.frame(Deposit=newD, Insecticide="B") )

> newProp.logC <- predict(ins.m1, type="response",

newdata=data.frame(Deposit=newD, Insecticide="C") )

> lines( newProp.logA ~ newD, lty=1); lines( newProp.logB ~ newD, lty=2)

> lines( newProp.logC ~ newD, lty=3)

Before evaluating this model, we pause to demonstrate the estimation of

ed50. The function dose.p() requires the name of the model, and the loca-

tion of the coeﬃcients that refer to the intercept and the slope. For insecti-

cide A:

> dose.p(ins.m1, c(1, 2))

Dose SE

p = 0.5: 5.099708 0.2468085

For other insecticides, the intercept term is not contained in a single param-

eter. However, consider ﬁtting an equivalent model:

> ins.m1A <- update( ins.m1, .~. - 1) # Do not fit a constant term

> coef( ins.m1A )

Deposit InsecticideA InsecticideB InsecticideC

0.6316762 -3.2213638 -2.8518371 -0.5333477

Fitting the model without β

forces r to ﬁt a model with separate intercept

terms for each insecticide. Then, being careful to give the location of the

intercept term ﬁrst:

> ED50s <- cbind( dose.p(ins.m1A, c(2, 1)), dose.p(ins.m1A, c(3, 1)),

dose.p(ins.m1A, c(4, 1)) )

> colnames(ED50s) <- c("Insect. A","Insect. B", "Insect. C"); ED50s

Insect. A Insect. B Insect. C

p = 0.5: 5.099708 4.514714 0.8443372

Returning now to the diagnostic analysis of the model, close inspection of

the top left panel in Fig. 9.9 shows model ins.m1 is inadequate. The pattern

in the residuals is easier to see in the top right panel:

9.11 Case Study 357

> library(statmod) # For qresid()

> plot( qresid(ins.m1) ~ fitted(ins.m1), type="n", las=1, ylim=c(-3, 3),

main="Quantile resids. plotted\nagainst fitted values",

xlab="Fitted values", ylab="Residuals")

> abline(h = 0, col="grey")

> points( qresid(ins.m1) ~ fitted(ins.m1), pch="A", type="b", lty=1,

subset=(deposit$Insecticide=="A") )

> points( qresid(ins.m1) ~ fitted(ins.m1), pch="B", type="b", lty=2,

subset=(deposit$Insecticide=="B") )

> points( qresid(ins.m1) ~ fitted(ins.m1), pch="C", type="b", lty=3,

subset=(deposit$Insecticide=="C"))

For each insecticide, the proportions are under-estimated at the lower and

higher values of deposit. Plotting the log-odds against the deposit shows the

relationship is not linear on the log-odds scale (Fig. 9.9, bottom panel):

> LogOdds <- with(deposit, log(Prop/(1-Prop)) )

> plot( LogOdds ~ Deposit, type="n", xlab="Deposit", data=deposit,

main="Logits plotted\nagainst Deposit", las=1)

> points( LogOdds ~ Deposit, pch="A", type="b", lty=1,

data=deposit, subset=(Insecticide=="A") )

> points( LogOdds ~ Deposit, pch="B", type="b", lty=2,

data=deposit, subset=(Insecticide=="B") )

> points( LogOdds ~ Deposit, pch="C", type="b", lty=3,

data=deposit, subset=(Insecticide=="C") )

As suggested earlier (Sect. 9.2), the logarithm of the dose is commonly used

in dose–response models, so we try such a model (Fig. 9.10, top left panel):

> deposit$logDep <- log( deposit$Deposit )

> ins.m2 <- glm(Killed/Number ~ logDep + Insecticide - 1,

family = binomial, weights = Number, data = deposit)

The ed50 estimates are on the log-scale for this model:

> ED50s <- cbind( dose.p(ins.m2, c(2, 1)), dose.p(ins.m2, c(3, 1)),

dose.p(ins.m2, c(4, 1)) )

> colnames(ED50s) <- c("Insect. A","Insect. B", "Insect. C"); exp(ED50s)

Insect. A Insect. B Insect. C

p = 0.5: 4.688232 4.154625 1.753202

The ed50 estimates are quite diﬀerent from those computed using model

ins.m1A.

While model ins.m2 is an improvement over model ins.m1, proportions

are still under-estimated for all types at the lower and higher values of deposit

(Fig. 9.10, top right panel).

Plotting the log-odds against the logarithm of Deposit indicates that the

log-odds are not constant, but are perhaps quadratic (Fig. 9.10, bottom panel;

code not shown). Because of this, we try this model:

> ins.m3 <- glm(Killed/Number ~ poly(logDep, 2) + Insecticide,

family = binomial, weights = Number, data = deposit)

358 9 Models for Proportions: Binomial GLMs

0.8 1.2 1.6 2.0

0.0

0.2

0.4

0.6

0.8

1.0

Proportion of Insects killed

log( Deposit )

Proportion killed

0.2 0.4 0.6 0.8 1.0

−3

−2

−1

Quantile resids. plotted

against fitted values

Fitted values

Residuals

0.8 1.2 1.6 2.0

−2

Logits plotted

against log(Deposit)

log(Deposit)

log−odds

Insecticide A

Insecticide B

Insecticide C

Fig. 9.10 The binomial glms for the insecticide data using the logarithm of deposit as

an explanatory variable in model ins.m2. Top left panel: the log-odds against the loga-

rithm of deposit showing the ﬁtted models; top right panel: the quantile residuals plotted

against the ﬁtted values; bottom panel: the log-odds plotted against the logarithm of

deposit (Sect. 9.11)

Now compare the two models involving logDep:

> anova( ins.m2, ins.m3, test="Chisq")

Analysis of Deviance Table

Model 1: Killed/Number ~ logDep + Insecticide - 1

Model 2: Killed/Number ~ poly(logDep, 2) + Insecticide

Resid. Df Resid. Dev Df Deviance Pr(>Chi)

1 14 23.385

2 13 15.090 1 8.2949 0.003976 **

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

9.11 Case Study 359

0.8 1.2 1.6 2.0

0.0

0.2

0.4

0.6

0.8

1.0

Proportion of Insects killed

log( Deposit )

Proportion killed

0.2 0.4 0.6 0.8 1.0

−2

−1

Quantile resids. plotted

against fitted values

Fitted values

Residuals

0.8 1.2 1.6 2.0

−2

Logits plotted

against log(Deposit)

log(Deposit)

log odds

Insecticide A

Insecticide B

Insecticide C

Fig. 9.11 The binomial glms for the insecticide data using the square of the logarithm

of deposit as an explanatory variable in model ins.m3. Top left panel: the log-odds

against the logarithm of deposit showing the ﬁtted models; top right panel: the quantile

residuals plotted against the ﬁtted values; bottom panel: the log-odds plotted against

the logarithm of deposit (Sect. 9.11)

This quadratic model is a statistically signiﬁcantly improvement; the plotted

lines appear much better (Fig. 9.11):

> newD <- seq( min(deposit$logDep), max(deposit$logDep), length=200)

> newProp4.logA <- predict(ins.m3, type="response",

newdata=data.frame(logDep=newD, Insecticide="A") )

> newProp4.logB <- predict(ins.m3, type="response",

newdata=data.frame(logDep=newD, Insecticide="B") )

> newProp4.logC <- predict(ins.m3, type="response",

newdata=data.frame(logDep=newD, Insecticide="C") )

> lines( newProp4.logA ~ newD, lty=1); lines( newProp4.logB ~ newD, lty=2)

> lines( newProp4.logC ~ newD, lty=3)

The ed50 for this quadratic model cannot be computed using dose.p (be-

cause of the quadratic term in logDep), but can be found using simple algebra

(Problem 9.3).

360 9 Models for Proportions: Binomial GLMs

The structural changes to the model show that the model now is adequate

(diagnostic plots not shown). No evidence exists to support overdispersion:

> c( deviance( ins.m3 ), df.residual( ins.m3 ) )

[1] 15.09036 13.00000

However, the saddlepoint approximation is probably not satisfactory and so

this conclusion may not be entirely trustworthy:

> c( min( deposit$Killed ), min( deposit$Number - deposit$Killed) )

[1]20

9.12 Using R to Fit GLMs to Proportion Data

Binomial glms are ﬁtted in r using glm() with family=binomial(). The link

functions "logit" (the default), "probit", "cloglog" (the complementary

log-log), "log" and "cauchit" are permitted. The response for a binomial

glm can be supplied in one of three ways:

• glm( y ~ x, weights=m, family=binomial), where y are the observed

proportions of successes in m trials.

• glm( cbind(success, fail) ~ x, family=binomial), where success

is a column of the number of successes, and fail is a column of the cor-

responding number of failures.

• glm( fac ~ x, family=binomial), where fac is a factor. The ﬁrst level

denotes failure and all other levels denote successes, or where fac consists

of logicals (either TRUE, which is treated as the success, or FALSE). Each

individual in the study is represented by one row. This ﬁts a Bernoulli

glm.

9.13 Summary

Chapter 9 considers ﬁtting binomial glms. Proportions may be modelled

using the binomial distribution (Sect. 9.2) where μ is the expected proportion

where 0 <μ<1, and y =0, 1/m, 2/m,...,1. The prior weights are w =

m. The residual deviance is suitably described by a χ

n−p



distribution if

min{m

}≥3 and min{m

(1 − μ

)}≥3.

Commonly-used link functions are the logit (the canonical link function),

probit and complementary log-log link functions (Sects. 9.3 and 9.4). Using

the logistic link function enables an interpretation in terms of odds μ/(1 −μ)

and odds ratios (or) (Sect. 9.5).

The median eﬀective dose (ed50) is the value of the covariates when the

expected proportion is μ =0.5 (Sect. 9.6).

9.13 Summary 361

Overdispersion is observed when the variation in the data is greater than

expected under the binomial model (Sect. 9.8). If overdispersion is observed,

a quasi-binomial model may be ﬁtted, which assumes V (μ)=φμ(1 − μ).

Overdispersion causes the estimates of the standard error to be underesti-

mated and conﬁdence intervals for parameters to be too narrow (Sect. 9.8).

For binomial glms, the Wald tests can fail in circumstances where one or

more of the regression parameters tend to ±∞ (Sect. 9.9).

Problems

Selected solutions begin on p. 539.

9.1. Suppose the proportion y has the binomial distribution so that z ∼

Bin(μ, m) where z = my is the number of successes. Show that the trans-

formation y

∗

=sin

−1

√

y produces approximately constant variance, by ﬁrst

expanding the transformation about μ using a Taylor series. (Hint: Follow

the steps outlined in Sect. 5.8.)

9.2. Suppose that a given dose–response experiment records the dose of poi-

son d and proportion y of insects out of m that are killed at each dose, such

that the model has the systematic component g(η)=β

+ β

1. Show that the ed50 for such a model using a probit link function is

ed50 = −β

/β

2. Show that the ed50 for such a model using the complementary log-log

link function is ed50 = {log(log 2) − β

}/β

3. Show that the ed50 for such a model using the logarithmic link function

is ed50 = (log 0.5 − β

)/β

9.3. Consider a binomial glm using a logistic link function with systematic

component logit(μ)=β

+ β

log x + β

(log x)

1. For this model, deduce a formula for estimating the ed50.

2. Use this result to estimate the ed50 for the three insecticides using model

ins.m3 ﬁtted in Sect. 9.11.

9.4. In Sect. 9.3 (p. 336), the probit binomial glm was developed as a thresh-

old model. Here consider using the logistic distribution with mean μ and

variance σ

as the tolerance distribution. The logistic distribution has the

probability function

P(y; μ, σ

π exp{−(y −μ)π/(σ

√

3)}

√

1 + exp{−(y −μ)π/(σ

√

3)}

for −∞ <y<∞, −∞ <μ<∞ and σ>0.

362 9 Models for Proportions: Binomial GLMs

Tabl e 9 .6 The logistic regression model ﬁtted to data relating hypertension to sleep

apnoea-hypopnoea (Problem 9.5)

Variable

se(

)

Intercept −6.949 0.377

Age 0.805 0.0444

Sex 0.161 0.113

Body mass index 0.332 0.0393

Apnoea-hypopnoea index 0.116 0.0204

1. Show that the logistic distribution is not an edm.

2. Determine the cdf for the logistic distribution.

3. Plot the density function and cdf for the logistic distribution with mean 0

and variance 1. Also plot the same graphs for the normal distribution

with mean 0 and variance 1. Comment on the similarities and diﬀerences

between the two probability functions.

4. Using the logistic distribution as the tolerance distribution, show that

the threshold model in Sect. 9.4 corresponds to a binomial glm with a

logistic link function.

9.5. In a study [14] of the relationship between hypertension and sleep

apnoea-hypopnoea (breathing diﬃculties while sleeping), a logistic regression

model was ﬁtted. The dependent variable was the presence of hypertension.

The independent variables were dichotomized as follows: Age: 0 for 10 years

or under, and 1 otherwise; sex: 0 for females, and 1 for males; body mass in-

dex: 0 if under 5 kg/m

, and 1 otherwise; apnoea-hypopnoea index: 0 if fewer

than ten events per hour of sleep, and 1 otherwise. Age, sex and body mass

index are extraneous variables. The ﬁtted model is summarized in Table 9.6.

1. Write down the ﬁtted model.

2. Use a Wald test to test if β

= 0 for each independent variable. Which

variables seems important in the model?

3. Find 95% conﬁdence intervals for each regression parameter.

4. Compute and interpret the odds ratios for each independent variable.

5. Predict the mean probability of observing hypertension in 30 year-old

males with a bmi of 6 kg/m

who have an apnoea-hypopnoea index value

of 5.

9.6. A study of stress and aggression in youth [15] measured the ‘role stress’

(an additive index from survey responses) and adolescent aggression levels (1

if the subject had engaged in at least one aggressive act as a youth, and 0

otherwise) in non-Hispanic whites. The response variable was aggression as

an adult (1 if the subject had engaged in at least one aggressive act, and 0

otherwise). The ﬁtted model is summarized in Table 9.7. (A number of other

extraneous variables are also ﬁtted, such as marital status and illicit drug

use, but are not displayed in the table.)

9.13 Summary 363

Tabl e 9 .7 Two binomial glms ﬁtted to the aggression data (Problem 9.6)

Males Females

Variable

se(

)

se(

)

Intercept 0.45 0.40 −0.22 0.53

Role stress, RS 0.04 0.08 0.26 0.06

Adolescent aggression, AA 0.25 0.15 0.82 0.19

Interaction, RS.AA 0.23 0.17 −0.22 0.11

Residual deviance 57.40 121.67



13 13

n 1323 1427

1. Write down the two ﬁtted models (one for males, one for females).

2. Use a Wald statistic to test if β

= 0 for the interaction terms for both

the male and female models. Comment.

3. The residual deviances for the ﬁtted logistic regression models without

the interaction term are 53.40 (males) and 117.82 (females). Use a likeli-

hood ratio test to determine if the interaction terms are necessary in the

models. Compare with the results of the Wald test.

4. Find 95% conﬁdence intervals for both interaction terms.

5. Compute and interpret the odds ratios for AA.

6. Is overdispersion likely to be a problem for the models shown in the table?

7. Suppose a logistic glm was ﬁtted to the data with role stress, adoles-

cent aggression, gender (G) and all the extraneous variables ﬁtted to the

model. Do you think the regression parameter for the three-way interac-

tion RS.AA.G would be diﬀerent from zero? Explain.

9.7. After the explosion of the space shuttle Challenger on January 28, 1986,

a study was conducted [1, 4] to determine if previously-collected data about

the ambient air temperature at the time of launch could have been used to

foresee potential problems with the launch (Table 4.1; data set: shuttles).

In Example 4.2, a model was proposed for these data.

1. Plot the data.

2. Fit and interpret the proposed model.

3. Perform a diagnostic analysis.

4. On the day of the Challenger launch, the forecast temperature was 31

◦

What is the predicted probability of an O-ring failure?

5. What would the ed50 mean in this context? What would be a more

sensible ed for this context?

9.8. An experiment [11] studied the survival of mice after receiving a test

dose of culture with ﬁve diﬀerent doses of antipneumococcus serum (in cc)

(Table 9.8; data set: serum).

364 9 Models for Proportions: Binomial GLMs

Tabl e 9 .8 The number of mice surviving exposure to pneumococcus after receiving a

dose of antipneumococcus (Problem 9.8)

Dose Total number Number of

(in cc) of mice survivors

0.000625 40 7

0.00125 40 18

0.0025 40 32

0.005 40 35

0.01 40 38

Tabl e 9.9 The number of tobacco budworm moths (Heliothis virescens) out of 20 that

were killed when exposed for three days to pyrethroid trans-cypermethrin (Problem 9.9)

Pyrethroid dose (in μg)

Gender12481632

Male 149131820

Female026101216

1. Fit and interpret a logistic regression model to the data with systematic

component Survivors/Number ~ 1 + log(Dose).

2. Examine the diagnostics from the above model.

3. Plot the data with the ﬁtted lines, and the corresponding 95% conﬁdence

intervals.

4. Estimate the ed50.

5. Interpret your ﬁtted model using the threshold interpretation for the link

function.

9.9. The responses of the tobacco budworm Heliothis virescens to doses

of pyrethroid trans-cypermethrin were recorded (Table 9.9; data set:

budworm)[2, 23] from a small experiment. Twenty male and twenty fe-

male moths were exposed at each of six doses of the pyrethroid, and the

number killed was recorded.

1. Plot survival proportions against dose, distinguishing male and female

moths. Explain why using the logarithms of dose as a covariate is sensible

given the values used for the pyrethroid dose.

2. Fit a binomial glm to the data, ensuring a diagnostic analysis. Begin by

ﬁtting a model with a systematic component of the form 1 + log2(Dose)

* Gender, and show that the interaction term is not signiﬁcant. Hence

reﬁt the model with systematic component 1 + log2(Dose) + Gender.

3. Plot the ﬁtted lines on the plot of the data (distinguishing between males

and females) and comment on the suitability of the model.

4. Determine the odds ratio for comparing the odds of a male moth dying

to the odds to a female moth dying.

9.13 Summary 365

Tabl e 9.1 0 The gender of candidates in the 1992 British general election; M means

males and F means females (Problem 9.10)

Cons Labour Lib-Dem Greens Other

Region M F M F M F M F M F

SouthEast1018842581 2842158627

South West 45 3 36 12 35 13 21 6 61 11

Great London 76 8 57 27 63 19 37 13 93 21

East Anglia 19 1 16 4 16 4 6 4 23 8

East Midlands 39 3 35 7 36 6 8 3 19 7

Wales 36 2 34 4 30 8 7 0 44 10

Scotland 63 9 67 5 51 21 14 6 87 17

WestMidlands508431549 9114305

Yorks and Humbers 51 3 45 9 42 12 22 3 22 6

North West 65 8 57 16 61 12 17 5 75 20

North 32 4 34 2 32 4 7 1 6 3

5. Determine if there is any evidence of a diﬀerence in the mortality rates

between the male and female moths.

6. Determine estimates of the ed50 for both genders.

7. Determine the 90% conﬁdence interval for the gender eﬀect.

9.10. The Independent newspaper tabulated the gender of all candidates run-

ning for election in the 1992 British general election (Table 9.10; data set:

belection)[6].

1. Plot the proportion of female candidates against the Party, and comment.

2. Plot the proportion of female candidates against the Region, and com-

ment.

3. Find a suitable binomial glm, ensuring a diagnostic analysis.

4. Is overdispersion evident?

5. Interpret the ﬁtted model.

6. Estimate and interpret the odds of a female candidate running for the

Conservative and Labour parties. Then compute the odds ratio of the

Conservative party ﬁelding a female candidate to the odds of the Labour

party ﬁelding a female candidate.

7. Determine if the saddlepoint approximation is likely to be suitable for

these data.

9.11. A study [9, 12] of patients treated for nonmetastatic sarcoma obtained

data on the gender of the patients, the presence of lymphocytic inﬁltration

and any asteoid pathology. The treatment was considered a success if pa-

tients were disease-free for 3 years (Table 9.11). Here, consider the eﬀect of

lymphocytic inﬁltration on the proportion of success.

1. Plot the proportion of successes against gender. Then plot the proportion

of successes against the presence or absence of lymphocytic inﬁltration.

Comment on the relationships.

366 9 Models for Proportions: Binomial GLMs

Tabl e 9 .11 The nonmetastatic sarcoma data (Problem 9.11)

Lymphotic Osteoid Group Number of

inﬁltration Gender pathology size m successes my

Absent Female Absent 3 3

Absent Female Present 2 2

Absent Male Absent 4 4

Absent Male Present 1 1

Present Female Absent 5 5

Present Female Present 5 3

Present Male Absent 9 5

Present Male Present 17 6

2. Fit the binomial glm using the gender and presence or absence of lym-

phocytic inﬁltration as explanatory variables. Show that the Wald test

results indicate that the eﬀect of lymphocytic inﬁltration is not signiﬁ-

cant.

3. Show that the likelihood ratio test indicates that the eﬀect of lymphocytic

inﬁltration is signiﬁcant.

4. Show that the score test also indicates that the eﬀect of lymphocytic

inﬁltration is signiﬁcant.

5. Explain the results from the three tests.

9.12. Chromosome aberration assays are used to determine whether or not

a substance induces structural changes in chromosomes. One study [24] com-

pared the results of two substances at various doses (Table 9.12). A large

number of cells were sampled at each dose to see how many were aberrant.

1. Fit a binomial glm to determine if there is evidence of a diﬀerence be-

tween the two substances.

2. Use the dose and the logarithm of dose as an explanatory variable in

separate glms, and compare. Which is better, and why?

3. Compute the 95% conﬁdence interval for the dose regression parameter,

and interpret.

4. Why would estimation of the ed50 be inappropriate?

9.13. A study [17] of the habitats of the noisy miner (a small but aggressive

native Australian bird; data set: nminer) recorded whether noisy miners were

present in various two hectare transects in buloke woodland patches (Miners),

and considered the following potential explanatory variables: the number of

eucalypt trees (Eucs); the number of buloke trees (Bulokes); the area of

contiguous remnant patch vegetation in which each site was located (Area);

whether the area was grazed (Grazed: 1 means yes); whether shrubs were

present in the transect (Shrubs: 1 means yes); and the number of pieces of

fallen timber (Timber). Part of this data frame was discussed in Example 1.5

(p. 14), where models were ﬁtted for the number of noisy miners.

REFERENCES 367

Tabl e 9 .12 The number of aberrant cells for diﬀerent doses of two substances (Prob-

lem 9.12)

Dose No. cell No. cells Dose No. cell No. cells

Substance (in mg/ml) samples aberrant Substance (in mg/ml) samples aberrant

A 0 400 3 B 0.0 400 5

A 20 200 5 B 62.5 200 2

A 100 200 14 B 125.0 200 2

A 200 200 4 B 250.0 200 4

B 500.0 200 7

Fit a suitable logistic regression model for predicting the presence of noisy

miners in two hectare transects in buloke woodland patches, ensuring an

appropriate diagnostic analysis. Also estimate the number of eucalypt trees

in which there is a greater than 90% chance of ﬁnding noisy miners.

9.14. In Example 9.4, data [3] were introduced regarding the germination

of seeds, using two types of seeds and two types of root stocks (Table 9.3).

An alternative way of entering the data is to record whether or not each

individual seed germinates or not (data set: germBin).

1. Fit the equivalent model to that ﬁtted in Example 9.4, but using data

prepared as in the data ﬁle germBin. This model is based on using a

Bernoulli distribution.

2. Show that both the Bernoulli and binomial glms produce the same values

for the parameter estimates and standard errors.

3. Show that the two models produce diﬀerent values for the residual dev-

iance, but the same values for the deviance.

4. Show that the two models produce similar results from the sequential

likelihood-ratio tests.

5. Compare the log-likelihoods for the binomial and Bernoulli distributions.

Comment.

6. Explain why overdispersion cannot be detected in the Bernoulli model.

References

[1] Chatterjee, S., Handcock, M.S., Simonoﬀ, J.S.: A Casebook for a First

Course in Statistics and Data Analysis. John Wiley and Sons, New York

(1995)

[2] Collett, D.: Modelling Binary Data. Chapman and Hall, London (1991)

[3] Crowder, M.J.: Beta-binomial anova for proportions. Applied Statistics

27(1), 34–37 (1978)

368 REFERENCES

[4] Dala, S.R., Fowlkes, E.B., Hoadley, B.: Risk analysis of the space shuttle:

pre-Challenger prediction of failure. Journal of the American Statistical

Association 84(408), 945–957 (1989)

[5] Dunn, P.K., Smyth, G.K.: Randomized quantile residuals. Journal of

Computational and Graphical Statistics 5(3), 236–244 (1996)

[6] Hand, D.J., Daly, F., Lunn, A.D., McConway, K.Y., Ostrowski, E.: A

Handbook of Small Data Sets. Chapman and Hall, London (1996)

[7] Hauck Jr., W.W., Donner, A.: Wald’s test as applied to hypotheses in

logit analysis. Journal of the American Statistical Association 72, 851–

853 (1977)

[8] Hewlett, P.S., Plackett, T.J.: Statistical aspects of the independent joint

action of poisons, particularly insecticides. II Examination of data for

agreement with hypothesis. Annals of Applied Biology 37, 527–552

(1950)

[9] Hirji, K.F., Mehta, C.R., Patel, N.R.: Computing distributions for ex-

act logistic regression. Journal of the American Statistical Association

82(400), 1110–1117 (1987)

[10] Hu, Y., Smyth, G.K.: ELDA: Extreme limiting dilution analysis for com-

paring depleted and enriched populations in stem cell and other assays.

Journal of Immunological Methods 347, 70–78 (2009)

[11] Irwin, J.O., Cheeseman, E.A.: On the maximum-likelihood method of

determining dosage-response curves and approximations to the median-

eﬀective dose, in cases of a quantal response. Supplement to the Journal

of the Royal Statistical Society 6(2), 174–185 (1939)

[12] Kolassa, J.E., Tanner, M.A.: Small-sample conﬁdence regions in expo-

nential families. Biometrics 55(4), 1291–1294 (1999)

[13] Krzanowski, W.J.: An Introduction to Statistical Modelling. Arnold,

London (1998)

[14] Lavie, P., Herer, P., Hoﬀstein, V.: Obstructive sleep apnoea syndrome as

a risk factor for hypertension: Population study. British Medical Journal

320(7233), 479–482 (2000)

[15] Liu, R.X., Kaplan, H.B.: Role stress and aggression among young adults:

The moderating inﬂuences of gender and adolescent aggression. Social

Psychology Quarterly 67(1), 88–102 (2004)

[16] Lumley, T., Kronmal, R., Ma, S.: Relative risk regression in medical

research: Models, contrasts, estimators, and algorithms. uw Biostatistics

Working Paper Series 293, University of Washington (2006)

[17] Maron, M.: Threshold eﬀect of eucalypt density on an aggressive avian

competitor. Biological Conservation 136, 100–107 (2007)

[18] Mather, K.: The analysis of extinction time data in bioassay. Biometrics

5(2), 127–143 (1949)

[19] Myers, R.H., Montgomery, D.C., Vining, G.G.: Generalized Linear Mod-

els with Applications in Engineering and the Sciences. Wiley Series in

Probability and Statistics. Wiley, Chichester (2002)

REFERENCES 369

[20] Nelson, W.: Applied Life Data Analysis. John Wiley and Sons, New York

(1982)

[21] Shackleton, M., Vaillant, F., Simpson, K.J., Sting, J., Smyth, G.K.,

Asselin-Labat, M.L., Wu, L., Lindeman, G.J., Visvader, J.E.: Gener-

ation of a functional mammary gland from a single stem cell. Nature

439, 84–88 (2006)

[22] Singer, J.D., Willett, J.B.: Applied Longitudinal Data Analysis: Model-

ing Change and Event Occurrence. Oxford University Press, New York

(2003)

[23] Venables, W.N., Ripley, B.D.: Modern Applied Statistics with S, fourth

edn. Springer-Verlag, New York (2002). URL http://www.stats.ox.ac.

uk/pub/MASS4

[24] Williams, D.A.: Tests for diﬀerences between several small proportions.

Applied Statistics 37(3), 421–434 (1988)

[25] Xie, G., Roiko, A., Stratton, H., Lemckert, C., Dunn, P., Mengersen,

K.: Guidelines for use of the approximate beta-Poisson dose-response

models. Risk Analysis 37, 1388–1402 (2017)

Chapter 10

Models for Counts: Poisson and

Negative Binomial GLMs

Poor data and good reasoning give poor results.

Good data and poor reasoning give poor results.

Poor data and poor reasoning give rotten results.

E. C. Berkeley [4,p.20]

10.1 Introduction and Overview

The need to count things is ubiquitous, so data in the form of counts arise

often in practice. Examples include: the number of alpha particles emitted

from a source of radiation in a given time; the number of cases of leukemia

reported per year in a certain jurisdiction; the number of ﬂaws per metre of

electrical cable. This chapter is concerned with counts when the individual

events being counted are independent, or nearly so, and where there is no

clear upper limit for the number of events that can occur, or where the upper

limit is very much greater than any of the actual counts. We ﬁrst compile

important information about the Poisson distribution (Sect. 10.2), the dis-

tribution most often used with count data. Poisson regression, or models for

count data described by covariates, has already been covered in Sect. 8.12 and

elsewhere. In this chapter, we then focus on describing the models for three

types of count data: models for count data described by covariates, models

for rates (Sect. 10.3) and models for counts organized in tables (Sect. 10.4).

Overdispersion is discussed in Sect. 10.5, including a discussion of negative

binomial glms and quasi-Poisson models as alternative models.

10.2 Summary of Poisson GLMs

The distribution most often used for modelling counts is the Poisson distri-

bution, which has the probability function

P(y; μ)=

exp(−μ)μ

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_10

371

372 10 Models for Counts: Poisson and Negative Binomial GLMs

for y =0, 1, 2,..., with expected counts μ>0. The Poisson distribution

has already been established as an edm (Example 5.2), and a Poisson glm

proposed for the noisy miner data in Example 1.5. Useful information about

the Poisson distribution appears in Table 5.1. The unit deviance for the

Poisson distribution is

d(y, μ)=2



y log

− (y − μ)



when the residual deviance is D(y, ˆμ)=



i=1

d(y

, ˆμ

), where w

are the

prior weights. When y = 0, the limit form of the unit deviance (5.14) is used.

By the saddlepoint approximation, D(y, ˆμ) ∼ χ

n−p



where p



is the number

of coeﬃcients in the linear predictor. The approximation is adequate if y

≥ 3

for all i (Sect. 7.5,p.276).

The most common link function used for Poisson glms is the logarithmic

link function (which is also the canonical link function), which ensures μ>0

and enables the regression parameters to be interpreted as having multiplica-

tive eﬀects. Using the logarithmic link function ("log" in r), the general form

of a Poisson glm is



y ∼ Pois(μ)

log μ = β

+ β

+ ···+ β

(10.1)

The systematic component of (10.1) can be written as

μ =exp(β

+ β

+ ···+ β

)

=expβ

× (exp β

)

× (exp β

)

×···×(exp β

)

This shows that the impact of each explanatory variable is multiplicative.

Increasing x

by one increases μ by factor of exp(β

). If β

= 0 then exp(β

1andμ is not related to x

.Ifβ

> 0 then μ increases if x

increases; if β

< 0

then μ decreases if x

increases.

Sometimes, the link functions "identity" (η = μ)or"sqrt" (η =

√

μ )

are used with Poisson glms. A Poisson glm is denoted glm(Pois; link), and

is speciﬁed in r using family=poisson() in the glm() call.

When the explanatory variables are all qualitative (that is, factors), the

data can be summarized as a contingency table and the model is often called

a log-linear model (Sect. 10.4). If any of the explanatory variables are quan-

titative (that is, covariates), the model is often called a Poisson regression

model. Since Poisson regression has been discussed earlier (Sect. 8.12), we do

not consider Poisson regression models further (but see Sect. 10.6 for a Case

Study).

10.3 Modelling Rates 373

When the linear predictor includes an intercept term (as is almost always

the case), and the log-link function is used, the residual deviance can be

simpliﬁed to

D(y, ˆμ)=2



i=1

log(y

/ˆμ

);

that is, the second term in the unit deviance can be dropped as it sums to

zero (Problem 10.2). This identity will be used later to clarify the analysis of

contingency tables.

For Poisson glms, the use of quantile residuals [12] is strongly recom-

mended (Sect. 8.3.4.2).

10.3 Modelling Rates

The ﬁrst context we consider is when the maximum number of events is

known but large; that is, there is an upper bound for each count response,

but the upper bound is very large. For such applications, the maximum num-

ber of events is usually representative of some population, and the response

can be usefully viewed as a rate rather than just as a count. The size of

each population needs to be speciﬁed to make comparisons meaningful. For

example, consider comparing the number of people with a certain disease in

various cities. The number of cases in each city may be useful information

for planning purposes. However, quoting just the number of people with the

disease in each city is an unfair comparison, as some cities have a far larger

population than others. Comparing the number of people with the disease per

unit of population (for example, per thousand people) is a fairer comparison.

That is, the disease rate is often more suitable for modelling than the actual

number of people with the disease.

In principle, rates can treated as proportions, and analysed using binomial

glms, but Poisson glms are more convenient when the populations are large

and the rates are relatively small, less than 1% say.

Example 10.1. As a numerical example, consider the number of incidents of

lung cancer from 1968 to 1971 in four Danish cities (Table 10.1; data set:

danishlc), recorded by age group [2, 26]. The number of cases of lung can-

cer in each age group is remarkably similar for Fredericia. However, using

the number of cases does not accurately reﬂect the information in the data

because ﬁve times as many people are in the 40–54 age group than in the

over-75 age group. Understanding the data is enhanced by considering the

rate of lung cancer, such as the number of lung cancer cases per unit of pop-

ulation. A plot of the cancer rates against city and age (Fig. 10.1) suggests

the lung cancer rate may change with age:

> data(danishlc)

> danishlc$Rate <- danishlc$Cases / danishlc$Pop * 1000 # Rate per 1000

> danishlc$Age <- ordered(danishlc$Age, # Ensure age-order is preserved

levels=c("40-54", "55-59", "60-64", "65-69", "70-74", ">74") )

374 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.1 Incidence of lung cancer in four Danish cities from 1968 to 1971 inclusive

(Example 10.1)

Fredericia Horsens Kolding Vejle

Age Cases Population Cases Population Cases Population Cases Population

40–54 11 3059 13 2879 4 3142 5 2520

55–59 11 800 6 1083 8 1050 7 878

60–64 11 710 15 923 7 895 10 839

65–69 10 581 10 834 11 702 14 631

70–74 11 509 12 634 9 535 8 539

Over 74 10 605 2 782 12 659 7 619

Age group

Cases/1000

40−54 55−59 60−64 65−69 70−74 >74

Fredericia

Horsens

Kolding

Vejle

Fig. 10.1 The Danish lung cancer rates for various age groups in diﬀerent cities

(Example 10.1)

> danishlc$City <- abbreviate(danishlc$City, 1) # Abbreviate city names

> matplot( xtabs( Rate ~ Age+City, data=danishlc), pch=1:4, lty=1:4,

type="b", lwd=2, col="black", axes=FALSE, ylim=c(0, 25),

xlab="Age group", ylab="Cases/1000")

> axis(side=1, at=1:6, labels=levels(danishlc$Age))

> axis(side=2, las=1); box()

> legend("topleft", col="black", pch=1:4, lwd=2, lty=1:4, merge=FALSE,

legend=c("Fredericia", "Horsens", "Kolding", "Vejle") )

The r function ordered() informs r that the levels of factor Age have a

particular order; without declaring Age as an ordered factor, Age is plotted

with ">74" as the ﬁrst level. The plots show no clear pattern by city, but the

lung cancer rate appears to grow steadily for older age groups for each city,

then falls away for the >74 age group. The lung cancer rate for Horsens in

the >74 age group seems very low.

An unfortunate side-eﬀect of declaring Age as an ordered factor is that

r uses polynomial contrasts for coding, which are not appropriate here (the

10.3 Modelling Rates 375

ordered categories are not equally spaced) and are hard to interpret anyway.

To instruct r to use the familiar treatment coding for ordered factors, use:

> options(contrasts= c("contr.treatment", "contr.treatment"))

The ﬁrst input tells r to use treatment coding for unordered factors (which

is the default), and the second to use treatment coding for ordered factors

(rather than the default "contr.poly").

Deﬁne y

as the observed number of lung cancers in group i where the

corresponding population is T

. The lung cancer rate per unit of population

is y

, and the expected rate is E[y

]=μ

, where μ

possibly depends

on the explanatory variables, and T

is known. Using a logarithmic link func-

tion, the suggested systematic component is log(μ

)=η

. Dropping the

subscript i, the model suggested for cancer rates is



y ∼ Pois(μ)

log μ = log T + β



j=1

where the explanatory variables x

are the necessary dummy variables re-

quired for the cities and age groups. The parameters β

must be estimated,

but no parameters need to be estimated for log T . In other words, the term

log T is an oﬀset (Sect. 5.5.2).

Fit the model in r as follows, starting with the interaction model:

> dlc.m1 <- glm( Cases ~ offset( log(Pop) ) + City * Age,

family=poisson, data=danishlc)

> anova(dlc.m1, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 23 129.908

City 3 3.393 20 126.515 0.33495

Age 5 103.068 15 23.447 < 2e-16 ***

City:Age 15 23.447 0 0.000 0.07509 .

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

We decide to retain only Age in the model.

> dlc.m2 <- update(dlc.m1, . ~ offset(log(Pop)) + Age )

An alternative model might consider Age as quantitative (since the cate-

gories are not equally spaced), using the lower class boundary of each class.

(The lower boundary are preferred since the ﬁnal class only has a lower

boundary; the class midpoint or upper boundary becomes subjective for the

ﬁnal class.)

> danishlc$AgeNum <- rep( c(40, 55, 60, 65, 70, 75), 4)

> dlc.m3 <- update(dlc.m1, . ~ offset( log(Pop) ) + AgeNum)

376 10 Models for Counts: Poisson and Negative Binomial GLMs

Figure 10.1 may suggest a possible quadratic relationship, but note the lower

class boundaries are not equally spaced:

> dlc.m4 <- update( dlc.m3, . ~ offset( log(Pop) ) + poly(AgeNum, 2) )

The quadratic model is an improvement over the model linear in AgeNum:

> anova( dlc.m3, dlc.m4, test="Chisq")

Analysis of Deviance Table

Model 1: Cases ~ AgeNum + offset(log(Pop))

Model 2: Cases ~ poly(AgeNum, 2) + offset(log(Pop))

Resid. Df Resid. Dev Df Deviance Pr(>Chi)

1 22 48.968

2 21 32.500 1 16.468 4.948e-05 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Since the models are not nested, we compare the four models using the

aic:

> c( "With interaction"=AIC(dlc.m1), "Without interaction"=AIC(dlc.m2),

"Age (numerical)"=AIC(dlc.m3), "Age (numerical; quadratic)"=AIC(dlc.m4) )

With interaction Without interaction

144.3880 136.6946

Age (numerical) Age (numerical; quadratic)

149.3556 134.8876

The aic suggests the quadratic model dlc.m4 produces the best predictions,

but the aic for models dlc.m2 and dlc.m4 are very similar.

The saddlepoint approximation is suitable for Poisson distributions when

> 3 for all observations. For these data:

> sort( danishlc$Cases )

[1]245677788910101010111111111112121314

[24] 15

which shows that the saddlepoint approximation may be suspect. However,

only one observation fails to meet this criterion, and only just, so we use the

goodness-of-ﬁt tests remembering to be cautious:

> D.m2 <- deviance(dlc.m2); df.m2 <- df.residual( dlc.m2 )

> c( Dev=D.m2, df=df.m2, P = pchisq( D.m2, df.m2, lower = FALSE) )

Dev df P

28.30652745 18.00000000 0.05754114

> D.m4 <- deviance(dlc.m4); df.m4 <- df.residual( dlc.m4 )

> c( Dev=D.m4, df=df.m4, P=pchisq( D.m4, df.m4, lower = FALSE) )

Dev df P

32.49959158 21.00000000 0.05206888

Both models are reasonably adequate. Consider the diagnostic plots

(Fig. 10.2), where the constant-information scale is from Table 8.1:

10.3 Modelling Rates 377

2.6 3.0 3.4

−3

−2

−1

Factor age model

Sqrt(Fitted values)

Standardized residuals

5101520

0.0

0.1

0.2

0.3

0.4

0.5

Cook's D

Index

Cook's distance, D

−2 −1 0 1 2

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

2.6 3.0 3.4

−3

−2

−1

Quadratic age model

Sqrt(Fitted values)

Standardized residuals

5101520

0.0

0.2

0.4

0.6

0.8

Cook's D

Index

Cook's distance, D

−2 −1 0 1 2

−3

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

Fig. 10.2 Diagnostic plots for two models ﬁtted model to the Danish lung cancer data.

Top panels: treating age as a factor (model dlc.m2); bottom panels: ﬁtting a quadratic

in age (model dlc.m4). The Q–Q plots use quantile residuals (Example 10.1)

> library(statmod) # For quantile residuals

> scatter.smooth( rstandard(dlc.m2) ~ sqrt(fitted(dlc.m2)),

ylab="Standardized residuals", xlab="Sqrt(Fitted values)",

main="Factor age model", las=1 )

> plot( cooks.distance(dlc.m2), type="h", las=1, main="Cook's D",

ylab="Cook's distance, D")

> qqnorm( qr<-qresid(dlc.m2), las=1 ); abline(0, 1)

> scatter.smooth( rstandard(dlc.m4) ~ sqrt(fitted(dlc.m4)),

ylab="Standardized residuals", xlab="Sqrt(Fitted values)",

main="Quadratic age model", las=1 )

> plot( cooks.distance(dlc.m4), type="h", las=1, main="Cook's D",

ylab="Cook's distance, D")

> qqnorm( qr<-qresid(dlc.m4), las=1 ); abline(0, 1)

The diagnostics suggest that both models are reasonable models, though we

prefer model dlc.m2, since model dlc.m4 appears to show three observations

with high inﬂuence relative to the other observations, and is a simpler model.



378 10 Models for Counts: Poisson and Negative Binomial GLMs

10.4 Contingency Tables: Log-Linear Models

10.4.1 Introduction

Count data commonly appear in tables, called contingency tables, where

the observations are cross-classiﬁed according to the levels of the classi-

fying factors. To discuss the issues relevant to contingency tables, we be-

gin with two cross-classifying factors (two-dimensional tables; Sect. 10.4.2

and 10.4.3) then extend to three cross-classifying factors (three-dimensional

tables; Sect. 10.4.4) and then extend to higher-order tables (Sect. 10.4.7).

10.4.2 Two Dimensional Tables: Systematic

Component

The simplest contingency table is a two-way (or two-dimensional) table, with

factors A and B. If factor A has I levels and factor B has J levels, the

contingency table has size I × J. In general, the entries in an I × J table

are deﬁned as shown in Table 10.2, where y

refers to the observed count in

row i and column j for i =1, 2,...I and j =1, 2,...J.

Write μ

for to the expected count in cell (i, j). For convenience, also

deﬁne π

as the expected probability that an observation is in cell (i, j),

where μ

= mπ

,andm is the total number of observations. We write m

i•

to mean the sum of counts in row i over all columns, and m

•j

to mean the

sum of counts in column j over all rows. The use of the dot • in this context

means to sum over all the elements of the index that the dot replaces.

If factors A and B are independent, then π

= π

i•

•j

is true. Writing

= mπ

i•

•j

, take logarithms to obtain

log μ

= log m + log π

i•

+ log π

•j

(10.2)

Table 10.2 The general I × J contingency table. The cell count y

corresponds to

level i of A and level j of B (Sect. 10.4.2)

Factor B

Column 1 Column 2 ··· Column J Total

Factor A

Row 1 y

··· y

1•

Row 2 y

··· y

2•

Row Iy

··· y

I•

Total m

•1

•2

··· m

•J

10.4 Contingency Tables: Log-Linear Models 379

Table 10.3 The attitude of Australians to genetically modiﬁed foods (factor A)ac-

cording to income (factor B) (Example 10.2)

High income Low income Total

=0) (x

=1)

For gm foods (x

= 0) 263 258 521

Against gm foods (x

= 1) 151 222 373

Total 414 480 894

for the systematic component. This systematic component may be re-

expressed using dummy variables, since the probabilities π

i•

depend on

which unique row the observation is in, and the probabilities π

•j

depends on

which unique column the observation is in.

Example 10.2. To demonstrate and ﬁx ideas, ﬁrst consider the smallest pos-

sible table of counts: a 2 ×2 table. The data in Table 10.3 were collected be-

tween December 1996 and January 1997, and comprise a two-dimensional (or

two-way) table of counts collating the attitude of Australians to genetically

modiﬁed (gm) foods (factor A) according to their income (factor B)[28, 31].

To analyse the data in r, ﬁrst deﬁne the variables:

> Counts <- c(263, 258, 151, 222)

> Att <- gl(2, 2, 4, labels=c("For", "Against") )

> Inc <- gl(2, 1, 4, labels=c("High", "Low") )

> data.frame( Counts, Att, Inc)

Counts Att Inc

1 263 For High

2 258 For Low

3 151 Against High

4 222 Against Low

The function gl() is used to generate factors by specifying the pattern in

the factor levels. The ﬁrst input indicates the number of levels, the second

input the number of times each level is repeated as a run according to how

the counts are deﬁned, and the third input is the length of the factor. The

labels input is optional, and deﬁnes the names for each level of the factor.

The variable Inc, for example, has two levels repeated one at a time (given

the order of the counts supplied in Counts), and has a length of four. As a

check, the contingency table in Table 10.3 canbecreatedusing

> gm.table <- xtabs( Counts ~ Att + Inc ); gm.table

Inc

Att High Low

For 263 258

Against 151 222

To test whether attitude is independent of income, a probabilistic model for

the counts is needed. A complete model for the data in Table 10.3 depends on

380 10 Models for Counts: Poisson and Negative Binomial GLMs

how the sample of individuals was collected. We will see in the next section

that a number of diﬀerent possible sampling scenarios lead us back to the

same basic statistical analysis. 

10.4.3 Two-Dimensional Tables: Random Components

10.4.3.1 Introduction

We now consider how the sample of individuals, tabulated in the contingency

table, was collected. In particular, we consider whether any or all of the

margins of the table were preset by the sampling scheme. A table of counts

may arise from several possible sampling schemes, each suggesting a diﬀerent

probability model. Three possible scenarios are:

•Them observations are allocated to factors A and B as the observations

randomly arrive; neither row nor column totals are ﬁxed.

• A ﬁxed total number of m observations are cross-classiﬁed by the factors

A and B.

• The row totals are ﬁxed, and observations allocated to factor B within

each level of A. (Alternatively, the column total are ﬁxed, and observa-

tions allocated to factor A within each level of B.)

10.4.3.2 No Marginal Totals Are Fixed

Firstly, assume no marginal totals are ﬁxed, as would be the case if, for

example, the data in Table 10.3 are collated from survey forms completed by

customers randomly arriving at a large shopping centre over 1 week. In this

scenario, no marginal total is ﬁxed; no limits exists on how large the counts

can be (apart from the city population, which is much larger than the counts

in the table).

If the total number of individuals observed (the grand total in the table)

can be viewed as Poisson distributed, and if the individuals give responses

independently of one another, then each of the counts in the table must follow

a Poisson distribution. The log-likelihood function for the 2 × 2 table is

(μ; y)=



i=1



j=1

(−μ

+ y

log μ

) , (10.3)

ignoring the terms not involving the parameters μ

. The residual deviance

D(y, ˆμ)=



i=1



j=1

log

ˆμ

, (10.4)

10.4 Contingency Tables: Log-Linear Models 381

omitting the term y

− ˆμ

, which always sums to zero if the log-linear pre-

dictor contains the constant term (Sect. 10.2).

Example 10.3. A Poisson model can be ﬁtted to the gm foods data

(Example 10.2)inr as follows:

> gm.1 <- glm( Counts ~ Att + Inc, family=poisson)

> anova( gm.1, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 3 38.260

Att 1 24.6143 2 13.646 7.003e-07 ***

Inc 1 4.8769 1 8.769 0.02722 *

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

(Recall the logarithmic link function is the default in r for the Poisson dis-

tribution.) This model ﬁts a log-linear model equivalent to (10.2), and hence

assumes that attitude and income are independent. Both Att and Inc are

statistically signiﬁcant in the order they are ﬁtted. The Poisson glm has the

coeﬃcients

> coef( gm.1 )

(Intercept) AttAgainst IncLow

5.4859102 -0.3341716 0.1479201

Thus the model has the systematic component

log ˆμ

=5.486 − 0.3342x

+0.1479x

, (10.5)

where x

=1forrowi = 2 (against gm foods) and is zero otherwise, and

= 1 for column j = 2 (low income) and is zero otherwise. (The r nota-

tion means, for example, that AttAgainst = 1 when the variable Att has

the value Against and is zero otherwise.) The systematic component in the

form of (10.5) is the usual regression model representation of the system-

atic component, where dummy variables are explicitly used for the rows and

columns. Since each cell of the table belongs to just one row and one column,

the dummy variables are often zero for any given cell.

Log-linear models are often easier to interpret when converted back to

the scale of the ﬁtted values. In particular, exp(

) gives the ﬁtted expected

count for the ﬁrst cell in the table, while similar expressions for the other

parameters give the relative increase in counts for one level of a factor over

the ﬁrst. By unlogging, the systematic component (10.5) becomes

ˆμ

=exp(5.486) × exp(−0.3342x

) × exp(0.1479x

)

= 241.3 × 0.7159

× 1.159

382 10 Models for Counts: Poisson and Negative Binomial GLMs

Compare the values of ˆμ

when x

= 1 to the values when x

=0:

When x

=0: ˆμ

= 241.3 × 0.7159

When x

=1: ˆμ

= 241.3 × 0.7159

× 1.159. (10.6)

Under this model, the ﬁtted values for ˆμ

are always 1.159 times the ﬁt-

ted values for ˆμ

, for either value of x

. From Table 10.3, the ratio of the

corresponding column marginal totals is

> sum(Counts[Inc=="Low"]) / sum(Counts[Inc=="High"])

[1] 1.15942

This value is exactly the factor in (10.6), which is no coincidence. This demon-

strates an important feature of the main eﬀects terms in log-linear models:

the main eﬀect terms in the model simply model the marginal totals. These

marginal totals are usually not of interest. The purpose of the gm study,

for example, is to determine the relationship between income and attitudes

towards gm foods, not to estimate the proportion of Australians with high

incomes. That is, the real interest lies with the interaction term in the model:

> gm.int <- glm( Counts ~ Att * Inc, family=poisson)

> anova( gm.int, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 3 38.260

Att 1 24.6143 2 13.646 7.003e-07 ***

Inc 1 4.8769 1 8.769 0.027218 *

Att:Inc 1 8.7686 0 0.000 0.003065 **

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The analysis of deviance table shows the interaction term is necessary in the

model. Notice that after ﬁtting the interaction term, no residual deviance

remains and no residual degrees of freedom remain, so the ﬁt is perfect. This

indicates that the number of coeﬃcients in the model is the same as the

number of entries in the table:

> length(coef(gm.int))

[1] 4

This means that the 2 × 2 table cannot be summarized by a smaller set of

model coeﬃcients. Since the interaction term is signiﬁcant, the data suggest

an association between income levels and attitude towards gm foods. We can

examine the percentage of low and high income respondents who are For and

Against gm foods by income level using prop.table():

> round(prop.table(gm.table, margin=2)*100, 1) # margin=2 means columns

Inc

Att High Low

For 63.5 53.8

Against 36.5 46.2

10.4 Contingency Tables: Log-Linear Models 383

This table shows that high income Australians are more likely to be in favour

of gm foods than low income Australians.

Observe that the main result of the model ﬁtting is that the interaction is

signiﬁcant (and hence that income and attitude to gm food are associated),

rather than the individual estimates of the regression parameters. 

10.4.3.3 The Grand Total Is Fixed

Another scenario that may have produced the data in Table 10.3 assumes a

ﬁxed number of 894 people were sampled. For example, the researchers may

have decided to survey 894 people in total, and then classify each respondent

as Low or High income, and also classify each respondent as For or Against

gm foods. While the counts are free to vary within the table, the counts

have the restriction that their sum is capped at 894. However, the Poisson

distribution has no upper limits on y by deﬁnition. Instead, the multinomial

distribution is appropriate. For a 2 ×2 table, the probability function for the

multinomial distribution is

P(y

; μ

,μ

)

Ignoring terms not involving μ

, the log-likelihood function is

(μ; y)=



i=1



j=1

log μ

, (10.7)

and the residual deviance is

D(y, ˆμ)=



i=1



j=1

log

ˆμ

, (10.8)

after ignoring terms not involving ˆμ

. Estimating μ

by maximizing the

log-likelihood for the multinomial distribution requires the extra condition



= m to ensure that the grand total is ﬁxed at



= m as

required by the sampling scheme.

Notice the similarity between the log-likelihood for the Poisson (10.3)and

multinomial (10.7) distributions: the ﬁrst term in (10.3) is the extra condition

to ensure the grand total is ﬁxed, and the second term is identical to (10.7).

The residual deviance is exactly the same for the Poisson (10.4) and multi-

nomial (10.7) distributions, after ignoring terms not involving μ

. These

similarities for the multinomial and Poisson distributions have one fortu-

nate implication: even though the multinomial distribution is the appropriate

384 10 Models for Counts: Poisson and Negative Binomial GLMs

probability model, a Poisson glm can be used to model the data under appro-

priate conditions. When the grand total is ﬁxed, the appropriate condition

is that the constant term β

must appear in the linear predictor, because

this ensures



i=1



j=1

ˆμ

= m (Problem 10.2). The eﬀect of including the

constant term in the model is that all inferences are conditional on the grand

total. The Poisson model, conditioning on the grand total, is equivalent to a

multinomial model. Thus, a Poisson model is still an appropriate model for

the randomness, provided the constant term is in the model.

10.4.3.4 The Column (or Row) Totals Are Fixed

A third scenario that may have produced the data in Table 10.3 assumes

that the column (or row) totals are ﬁxed. For example, the researchers may

have decided to survey 480 low income people and 414 high income people,

then record their attitudes towards gm foods. In this case, the totals in each

column are ﬁxed and the counts again have restrictions. For example, the

number of high income earners against gm foods is known once the number

of high income earners in favour of gm foodsisknown.

A multinomial distribution applies separately within each column of the

table, because the numbers in each column are ﬁxed and not random. Assum-

ing the counts in each column are independent, the probability function is

P(y

; μ

,μ

)

For column 1

  

•1



•1





•1



•2



•2





•2



  

Forcolumn2

(10.9)

where m

•j

is the total of column j. The log-likelihood function is

(μ; y)=



i=1



j=1

log μ

, (10.10)

when terms not involving the parameters μ

are ignored. To solve for the

parameters μ

, the extra constraints



i=1

= m

•1

and



i=1

= m

•2

must also be added to ensure both column totals are ﬁxed.

Again, notice the similarity between the log-likelihood (10.10) and the log-

likelihood for the Poisson (10.3). The residual deviances are exactly the same,

after ignoring terms not involving μ

. This means the Poisson distribution

10.4 Contingency Tables: Log-Linear Models 385

can be used to model the data, provided the coeﬃcients corresponding to the

row totals appear in the linear predictor, since this ensures

•2



i=1



i=1

ˆμ

Requiring β

in the model also ensures that



i=1

ˆμ

also, and so

the row totals are ﬁxed.

Similarly, if the column totals are ﬁxed, a Poisson glm is appropriate

if the coeﬃcients corresponding to the column totals are in the model. If

both the row and column totals are ﬁxed, a Poisson glm is appropriate if

the coeﬃcients corresponding to the row and column totals are in the linear

predictor.

These general ideas can be extended to larger tables. In general, a Poisson

glm can be ﬁtted to contingency table data provided the coeﬃcients in the

linear predictor corresponding to ﬁxed margins are included in the linear

predictor.

10.4.4 Three-Dimensional Tables

10.4.4.1 Introduction

Three-dimensional tables cross-classify subjects according to three factors,

say A, B and C. If the factors have I, J and K levels respectively, the table

is an I × J × K table. As an example, the entries in a 3 × 2 × 2 table are

deﬁned as shown in Table 10.2, where y

ijk

refers to the observed count in row i

(i =1, 2,...I ) and column j (j =1, 2,...J) for group k (k =1, 2,...K);

ijk

refers to the expected count in cell (i, j, k); and π

ijk

= μ

ijk

/m refers

to the expected probability that an observation is in cell (i, j, k). In other

words, Factor A has I levels, Factor B has J levels, and Factor C has K

levels (Table 10.4).

Table 10.4 The 3 ×2 ×2 contingency table. The cell count y

ijk

corresponds to level i

of A, level j of B and level k of C (Sect. 10.4.4)

Total B

Total Total B

Total B

Total

111

121

1•1

112

122

1•2

11•

12•

1••

211

221

2•1

212

222

2•2

21•

22•

2••

311

321

3•1

312

322

3•2

31•

32•

3••

Total m

•11

•21

••1

•12

•22

••2

•1•

•2•

386 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.5 The kidney stone data. The success rates of two methods are given by size;

S means a success, and F means a Failure (Example 10.4)

Small stones Large stones

SFTotal SFTotal Total S Total F Total

Method A 81 6 87 192 71 263 273 77 350

Method B 234 36 270 55 25 80 289 61 350

Total 315 42 357 247 96 343 562 138 700

The meaning of the main eﬀect terms in a Poisson glm has been discussed

in the two-dimensional context: the main eﬀect terms model the marginal to-

tals. Scientiﬁc interest focuses on the interactions between the factors. The

model with main-eﬀects only acts as the base model for contingency tables

against which interaction models are compared. In a three-dimensional table,

three two-factor interactions are possible, as well as an interaction term with

all three factors. Diﬀerent interpretations exist depending on which interac-

tion terms appear in the ﬁnal model. These interpretations are considered in

this section. We now introduce the example data to be used.

Example 10.4. The example data in this section (Table 10.5; data set:

kstones) comes from a study of treatments for kidney stones [8, 24], com-

paring the success rates of various methods for small and large kidney stones.

> data(kstones); str(kstones)

'data.frame': 8 obs. of 4 variables:

$ Counts : int 81 6 234 36 192 71 55 25

$ Size : Factor w/ 2 levels "Large","Small": 22221111

$ Method : Factor w/ 2 levels "A","B": 11221122

$ Outcome: Factor w/ 2 levels "Failure","Success": 21212121

We treat the method as factor A, the kidney stone size as factor B, and the

outcome (success or failure) as factor C.

Note that 350 patients were selected for use with each method. Since this

marginal total is ﬁxed, the corresponding main eﬀect term Method must ap-

pear in the Poisson glm. The Poisson glm with all three main eﬀect terms

ensures all the marginal totals from the original table are retained, but the

parameters themselves are of little interest. 

10.4.4.2 Mutual Independence

If A, B and C are independent, then π

ijk

= π

i••

× π

•j•

× π

••k

so that, on a

log-scale,

log μ

ijk

= log m + log π

i••

+ log π

•j•

+ log π

••k

10.4 Contingency Tables: Log-Linear Models 387

using that μ

ijk

= mπ

ijk

. This is called mutual independence. As seen for

the two-dimensional tables, including the main eﬀect terms eﬀectively en-

sures the marginal totals are preserved. If the mutual independence model is

appropriate, then the table may be understood from just the marginal totals.

For the kidney stone data, the mutual independence model states that the

success or failure is independent of the method used, and independent of the

size of the kidney stones, and that the method used is also independent of

the size of the kidney stone. Adopting this model assumes the data can be

understood for each variable separately. In other words, equal proportions

of patients are in each method; 138/700 = 19.7% of all treatments fail; and

343/700 = 49.0% of patients have large kidney stones. Fit the model using:

> ks.mutind <- glm( Counts ~ Size + Method + Outcome,

family=poisson, data=kstones)

In this section, we will ﬁt the models then comment and compare the models

after all the models are ﬁtted.

10.4.4.3 Partial Independence

Suppose A and B are not independent, but both are independent of C; then

ijk

= π

ij•

× π

••k

, or log μ

ijk

= log m + log π

ij•

+ log π

••k

on a log-scale.

Since A and B are not independent, π

ij•

= π

i••

× π

•j•

. To ensure that the

marginal totals are preserved, the main eﬀects are also included in the model

(along the lines of the marginality principle; Sect. 2.10.4). This means that

the model

log μ

ijk

= log m + log π

i••

+ log π

•j•

+ log π

••k

+ log π

ij•

is suggested. This systematic component has one two-factor interaction A.B.

This is called partial independence (or joint independence). If a partial inde-

pendence model is appropriate, then the two-way tables for each level of C are

multiples of each other, apart from randomness. The data can be understood

by combining the tables over C.

For the kidney stone data, we can ﬁt all three models that have one of the

two-factor interactions:

> ks.SM <- glm( Counts ~ Size * Method + Outcome,

family=poisson, data=kstones )

> ks.SO <- update(ks.SM, . ~ Size * Outcome + Method)

> ks.OM <- update(ks.SM, . ~ Outcome * Method + Size)

10.4.4.4 Conditional Independence

Suppose that A and B are independent of each other when considered sep-

arately for each level of C. Then the probabilities π

ijk

are independent

388 10 Models for Counts: Poisson and Negative Binomial GLMs

conditional on the level of k, when π

ij|k

= π

i•|k

× π

•j|k

. Each conditional

probability can be written in terms of marginal totals:

ij|k

ijk

••k

; π

i•|k

i•k

••k

; π

•j|k

•jk

••k

so that π

ijk

=(π

i•|k

× π

•j|k

)π

••k

= π

i•k

•jk

/π

••k

hold. In other words,

log μ

ijk

= log m + log π

i•k

+ log π

•jk

− log π

••k

on a log-scale. To ensure the

marginal totals are preserved, use the model

log μ

ijk

= log m + log π

i••

+ log π

•j•

+ log π

••k

+ log π

i•k

+ log π

•jk

which includes the main eﬀects. The systematic component has the two two-

factor interactions A.C and B.C. This is called conditional independence.

If a conditional independence model is appropriate, then each two-way

table for each level of C considered separately shows independence between

A and B. The data can be understood by creating separate tables involving

factors A and B, one for each level of C.

The three models with two of the two-factor interactions are:

> ks.noMO <- glm( Counts ~ Size * (Method + Outcome),

family=poisson, data=kstones )

> ks.noOS <- update(ks.noMO, . ~ Method * (Outcome + Size) )

> ks.noMS <- update(ks.noMO, . ~ Outcome * (Method + Size) )

10.4.4.5 Uniform Association

Consider the case where all three two-factor interactions are present but the

three-factor interaction A.B.C only is absent. This means that each two-

factor interaction is unaﬀected by the level of the third factor. No interpre-

tation in terms of independence or through the marginal totals is possible.

The model is

log μ

ijk

= log m + log π

i••

+ log π

•j•

+ log π

••k

+ log π

i•k

+ log π

•jk

+ log π

ij•

which contains all two-way interactions. This is called uniform association.

If the uniform association model is appropriate, then the data can be under-

stood by examining all three individual two-way tables. For the kidney stone

data the model with all of the two-factor interactions is:

> ks.no3 <- glm( Counts ~ Size*Method*Outcome - Size:Method:Outcome,

family=poisson, data=kstones )

Uniform association is simple enough to deﬁne from a mathematical point of

view, but is often diﬃcult to interpret from a scientiﬁc point of view.

10.4 Contingency Tables: Log-Linear Models 389

10.4.4.6 The Saturated Model

If all interaction terms are necessary in the linear predictor, the model is the

saturated model

log μ

ijk

= log m + log π

i••

+ log π

•j•

+ log π

••k

+ log π

i•k

+ log π

•jk

+ log π

ij•

+ log π

ijk

which includes all interactions. The model has zero residual deviance (in

computer arithmetic) and zero residual degrees of freedom. In other words,

the model produces a perfect ﬁt:

> ks.all <- glm( Counts ~ Size * Method * Outcome,

family=poisson, data=kstones )

> c( deviance( ks.all ), df.residual(ks.all) )

[1] -2.930989e-14 0.000000e+00

This means that there are as many parameter estimates as there are cells

in the table, and so the data cannot be summarized using a smaller set of

coeﬃcients. If the saturated model is appropriate, then the data cannot be

presented in a simpler form than giving the original I × J × K table.

10.4.4.7 Comparison of Mo dels

For the kidney stone data the saddlepoint approximation is suﬃciently ac-

curate since min{y

}≥3. This means that goodness-of-ﬁt tests can be used

to examine and compare the models (Table 10.6). The mutual independence

model and partial independence models are not appropriate, as the residual

deviance far exceeds the residual degrees of freedom. Model ks.noMO appears

the simplest suitable model. This implies that the data are best understood

by creating separate tables for large and small kidney stones, but small and

large kidney stones data should not be combined.

10.4.5 Simpson’s Paradox

Understanding which interaction terms are necessary in a log-linear model

has important implications for condensing the tabular data. If a table is col-

lapsed over a factor incorrectly, incorrect and misleading conclusions may be

reached. An extreme example of this is Simpson’s paradox. To explain, con-

sider the kidney stones data (Table 10.5). The most suitable model appears to

be model ks.noMO (Table 10.6). This model has two two-factor interactions,

indicating conditional independence between Outcome and Method, depend-

ing on the Size of the kidney stones. The dependence on Size means that

the data must be stratiﬁed by kidney stone size for the correct relationship

between Method and Outcome to be seen. Combining the data over Sizes, and

390 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.6 The ﬁtted values for all Poisson glms ﬁtted to the kidney stone data. Model

ks.noMO is the selected model and is ﬂagged * (Sect. 10.4.4)

Mutual Partial Conditional Uniform Saturated

independence independence independence association model

Count

ks.mutind

ks.SM

ks.SO

ks.OM

ks.noMO *

ks.noOS

ks.noMS

ks.no3

ks.all

81 143.369.8 157.5 139.276.867.9 153.079.081

635.217.221.039.310.219.123.48.06

234 143.3 216.8 157.5 147.4 238.2 222.9 162.0 236.0 234

36 35.253.221.031.131.847.118.634.036

192 137.7 211.2 123.5 133.8 189.4 205.1 120.0 194.0 192

71 33.851.848.037.773.657.953.669.

071

55 137.764.2 123.5 141.657.666.1 127.053.055

25 33.815.848.029.922.413.942.427.025

Res. dev.: 234.433.1 204.8 232.13.530.8 202.41.00

Res.df: 4 333 222 1 0

G-o-F P :0.00 0.00 0.00 0.00 0.18 0.00 0.00 0.32 1.00

hence considering a single combined two-way table of Method and Outcome

(and hence ignoring Size), is an incorrect summary. To demonstrate, consider

incorrectly collapsing the contingency table over Size. First, use xtabs() to

create a suitable three-dimensional table of counts:

> ks.tab <- xtabs(Counts ~ Method + Outcome + Size, data=kstones)

> ks.tab

, , Size = Large

Outcome

Method Failure Success

A 71 192

B2555

, , Size = Small

Outcome

Method Failure Success

A681

B 36 234

Then sum over Size, which is the third dimension:

> MO.tab <- apply( ks.tab, c(1, 2), sum) # Sums over the 3rd dimension

> MO.tab # An *incorrect* collapsing of the data

Outcome

Method Failure Success

A 77 273

B 61 289

10.4 Contingency Tables: Log-Linear Models 391

The table suggests that Method B has a higher success rate than Method A:

> prop.table(MO.tab, 1) # Compute proportions in each row (dimension 1)

Outcome

Method Failure Success

A 0.2200000 0.7800000

B 0.1742857 0.8257143

The overall success rate for Method A is about 78%, and for Method B the

success rate is about 83%, so we would prefer Method B. However, recall

that the table MO.tab is incorrectly collapsed over Size: the conditional in-

dependence suggest the relationship between Method and Outcome should be

examined separately for each level of Size.

Consequently, now examine the two-way table for large and small kidney

stones separately:

> MO.tab.SizeLarge <- ks.tab[, , "Large"] # Select Large stones

> prop.table(MO.tab.SizeLarge, 1) # Compute proportions in each row

Outcome

Method Failure Success

A 0.269962 0.730038

B 0.312500 0.687500

For large kidney stones, the success rate for Method A is about 73%, and for

Method B the success rate is about 69% so we would prefer Method A.

> MO.tab.SizeSmall <- ks.tab[, , "Small"] # Select Small stones

> prop.table(MO.tab.SizeSmall, 1) # Compute proportions in each row

Outcome

Method Failure Success

A 0.06896552 0.93103448

B 0.13333333 0.86666667

For small kidney stones, the success rate for Method A is about 93%, and for

Method B the success rate is about 87%, so we would prefer Method A.

In this example, incorrectly collapsing the table over Size has completely

changed the conclusion. Ignoring Size, Method B has a higher overall success

rate, but Method A actually has a higher success rate for both small and large

kidney stones. This is called Simpson’s paradox, which is a result of incorrectly

collapsing a table.

To explain the apparent paradox, ﬁrst notice that the large kidney stone

group reported a far lower success rate for both methods compared to the

small kidney stone group. Since Method A was used on a larger proportion of

patients with large kidney stones, Method A reports a high number of total

failures when the two groups are combined. In contrast, Method B was used

on a larger proportion of patients with small kidney stones, where the success

rate for both methods is better, and so Method B reports a smaller number

of total failures.

392 10 Models for Counts: Poisson and Negative Binomial GLMs

10.4.6 Equivalence of Binomial and Poisson GLMs

In many contingency table contexts, interest focuses on explaining one of the

factors in terms of the others. When the response factor of interest takes

two levels, interest focuses on explaining the proportion of responses that

are allocated to each of the two levels. In this case, there is a binomial glm

with the logistic link that is equivalent to the Poisson log-linear model. The

reason is that for large m and small proportions, the binomial distribution

approaches the Poisson distribution. To see this, write the probability of a

success in the binomial distribution as π. Then, the variance function for

the number of successes using the binomial model is V (π)=mπ(1 − π).

When π is small and m is large, V (π)=mπ(1 − π) → mπ.Thisisequiv-

alent to the variance of the Poisson distribution. This means that the bi-

nomial distribution approaches the Poisson distribution for large m and

small π.

For example, consider the data of Table 10.3 (p. 379) relating gm attitude

to income. Here interest focuses on whether income level aﬀects gm attitude,

so the data could be equally well analysed in r by treating Att as the response

variable:

> y <- ifelse(Att == "Against", 1, 0)

> gm.bin <- glm(y~Inc, family=binomial, weights=Counts)

> anova(gm.bin, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 3 1214.7

Inc 1 8.7686 2 1206.0 0.003065 **

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The deviance goodness-of-ﬁt test for Inc is identical to the test for Att:

Inc interaction given in Sect. 10.4.3.2, with the same P -value and the same

interpretation. The odds of being against gm foods are nearly 50% greater

for low-income respondents:

> coef(summary(gm.bin))

Estimate Std. Error z value Pr(>|z|)

(Intercept) -0.5548742 0.1021018 -5.434518 5.494476e-08

IncLow 0.4045920 0.1371323 2.950378 3.173854e-03

> exp(coef(gm.bin)["IncLow"])

IncLow

1.498691

Example 10.5. For the kidney stones data (Table 10.5; data set: kstones),

interest may focus on comparing the success rates of the two methods. From

this point of view, the data may be analysed via a binomial glm:

10.4 Contingency Tables: Log-Linear Models 393

> y <- ifelse(kstones$Outcome=="Success", 1, 0)

> ks.bin <- glm(y~Size*Method, family=binomial,

weights=Counts, data=kstones)

> anova(ks.bin, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 7 694.98

Size 1 29.6736 6 665.31 5.113e-08 ***

Method 1 2.4421 5 662.87 0.1181

Size:Method 1 1.0082 4 661.86 0.3153

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The analysis of deviance shows that success depends strongly on the size of

the kidney stones (better success for small stones), but there is no evidence for

any diﬀerence between the two methods, either overall or separately for small

or large stones. This conclusion agrees with the contingency table analysis,

which concluded that Outcome was conditionally independent of Method given

Size. The contingency table model ks.noMO contains the additional informa-

tion that Method is associated with Size. Indeed it is clear from Table 10.5

that Method A is predominately used for large stones and Method B for small

stones. Whether the ability to test for associations between explanatory fac-

tors, provided by the contingency table analysis, is of interest depends on the

scientiﬁc context. For these data, the choice of method is likely made based

on established hospital protocols, and hence would be known before the data

were collected. 

10.4.7 Higher-Order Tables

Extending these ideas to situations with more than three factors is easy in

practice using r, though interpreting the ﬁnal models is often diﬃcult.

Example 10.6. A study of seriously emotionally disturbed (sed) and learning

disabled (ld) adolescents [19, 29] reported their depression levels (Table 10.7;

data set: dyouth). The data are counts classiﬁed by four factors: Age (using

12-14 as the reference group), Group (either LD or SED), Gender and level

of Depression (either low L or high H). Since none of the totals were ﬁxed

beforehand and are free to vary randomly, no variables need to be included

in the model. With four factors,





= 6 two-factor interactions,





three-factor interactions and one four-factor interaction are potentially in the

model. As usual, the main-eﬀect terms are included in the model to ensure

the marginal totals are preserved.

394 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.7 Depression levels in youth (Example 10.6)

Depression low L Depression high H

Age Group Males Females Males Females

12-14 LD 79 34 18 14

SED 14 5 5 8

15-16 LD 63 26 10 11

SED 32 15 3 7

17-18 LD 36 16 13 1

SED 36 12 5 2

The most suitable model for the data [11] (Problem 10.8) appears to be:

> data(dyouth)

> dy.m1 <- glm( Obs ~ Age*Depression*Gender + Age*Group,

data=dyouth, family=poisson)

> anova(dy.m1, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 23 368.05

Age 2 11.963 21 356.09 0.002525 **

Depression 1 168.375 20 187.71 < 2.2e-16 ***

Gender 1 58.369 19 129.34 2.172e-14 ***

Group 1 69.104 18 60.24 < 2.2e-16 ***

Age:Depression 2 3.616 16 56.62 0.163964

Age:Gender 2 3.631 14 52.99 0.162718

Depression:Gender 1 7.229 13 45.76 0.007175 **

Age:Group 2 27.090 11 18.67 1.311e-06 ***

Age:Depression:Gender 2 8.325 9 10.35 0.015571 *

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The three-way interaction shows that the relationship between age and

depression is diﬀerent for males and females:

> Males <- subset(dyouth, Gender=="M")

> Females <- subset(dyouth, Gender=="F")

> table.M <- prop.table( xtabs(Obs~Age+Depression, data=Males), 1)

> table.F <- prop.table( xtabs(Obs~Age+Depression, data=Females), 1)

> round(table.F * 100) # FEMALES

Depression

Age H L

12-14 36 64

15-16 31 69

17-18 10 90

> round(table.M * 100) # MALES

Depression

Age H L

12-14 20 80

15-16 12 88

17-18 20 80

10.4 Contingency Tables: Log-Linear Models 395

Given the ﬁtted model, collapsing the table into a simpler table would be

misleading. The proportion tables show that the rate of high depression de-

creases with age for girls, especially for 17 years and older, whereas for males

the rate of high depression decreases at age 15–16 then increases again for

17–18. This diﬀerence in pattern explains the three-way interaction detected

by the analysis of deviance table.

The model also ﬁnds a signiﬁcant interaction between Age and Group,

meaning simply that the sed and ld groups contain diﬀerent proportions of

the age groups. This is not particularly of interest, but it is important to keep

the Age:Group term in the model, so that the tests for interactions involving

Depression should adjust for these demographic proportions.

Overall, the model shows an association between depression and age and

gender, but no diﬀerence in depression rates between the two groups once

the demographic variables have been taken into account. 

10.4.8 Structural Zeros in Contingency Tables

Contingency tables may contain cells with zero counts. Depending on the

reason for a zero count, diﬀerent approaches must be taken when modelling.

Sampling zeros or random zeros appear by chance, simply because no

observations occurred in that category. Larger samples may produce non-

zero counts in those cells. Computing ﬁtted values for these cells is sensible;

they are legitimate counts to be modelled like the other counts in the data.

However, the presence of the zeros means the saddlepoint approximation is

likely to be very poor. As a result, levels of one or more factors may be

combined to increase the minimum count. For example, ‘Strongly agree’ and

‘Agree’ may be combined sensibly into a single ‘Agreement’ category.

Structural zeros appear because the outcome is impossible. For example, in

a cross-tabulation of gender and surgical procedures, the cell corresponding

to male hysterectomies must contain a zero count. Producing ﬁtted values

for these cells makes no sense. Structural zeros are not common in practice.

Structural zeros require special attention since computing expected counts

for impossible events is nonsense. As a result, cells containing structural zeros

are removed from the data before analysis.

Example 10.7. The types of cancer diagnosed in Western Australia in 1996

were recorded for males and females (Table 10.8; data set: wacancer)to

ascertain whether the number of cancers diﬀers between genders [20].

Three cells have zeros recorded. Two of these three cells are structural

zeros since they are impossible—females cannot have prostate cancer, and

males cannot have cervical cancer. Breast cancer is a possible, but very rare,

disease among men (about 100 times as many cases in females compared to

males, in the usa [34, Table 1]). The zero for male breast cancer is technically

396 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.8 The number of cancers diagnosed by gender in Western Australia during

1996 (Example 10.7)

Cancer type

Gender Prostate Breast Colorectal Lung Melanoma Cervix Other

Males 923 0 511 472 362 0 1406

Females 0 875 355 211 282 77 1082

a sampling zero. Since breast cancer is already known to be a rare disease

for males, the analysis should focus on gender diﬀerences for other types of

cancers, such as colorectal, lung, melanoma and other cancers.

To begin, we ﬁt a model ignoring these complications:

> data(wacancer)

> wc.poor <- glm( Counts ~ Cancer*Gender, data=wacancer, family=poisson )

> anova( wc.poor, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 13 6063.7

Cancer 6 3281.5 7 2782.2 < 2.2e-16 ***

Gender 1 95.9 6 2686.2 < 2.2e-16 ***

Cancer:Gender 6 2686.2 0 0.0 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

To compare, we now remove breast cancer, male cervical cancer and female

prostate cancer from the analysis, and reﬁt:

> # Omit necessary cells of table:

> wc <- subset(wacancer, (Cancer!="Breast"))

> wc <- subset(wc, !(Cancer=="Cervix" & Gender=="M"))

> wc <- subset(wc, !(Cancer=="Prostate" & Gender=="F"))

> xtabs(Counts~Gender+Cancer, data=wc) # Table *looks* similar

Cancer

Gender Breast Cervix Colorectal Lung Melanoma Other Prostate

F 0 77 355 211 282 1082 0

M 0 0 511 472 362 1406 923

> # Now fit the model

> wc.m1 <- glm( Counts ~ Cancer*Gender, data=wc, family=poisson )

> anova( wc.m1, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 9 2774.32

Cancer 5 2591.47 4 182.85 < 2.2e-16 ***

Gender 1 144.74 3 38.11 < 2.2e-16 ***

Cancer:Gender 3 38.11 0 0.00 2.68e-08 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

An alternative to explicitly removing these observations from the table is to

set the corresponding prior weights weights to zero for these observations,

and to one for other observations. Even though the prior weighs are deﬁned to

10.5 Overdispersion 397

be positive, r interprets a prior weight of zero to mean that the corresponding

observation should be ignored in the analysis.

For both models, the interaction term is very signiﬁcant, so the number

of people diagnosed with the diﬀerent types of cancers diﬀers according to

gender, even after eliminating prostate, breast and cervical cancer, which

are obviously gender-linked. However, note that the degrees of freedom are

diﬀerent for the two models. 

10.5 Overdispersion

10.5.1 Overdispersion for Poisson GLMs

For a Poisson distribution, var[y]=μ. However, in practice the apparent

variance of the data often exceeds μ. This is called overdispersion,ashas

already been discussed for binomial glms (Sect. 9.8). Underdispersion also

occurs, but is less common.

Overdispersion arises either because the mean μ retains some innate vari-

ability, even when all the explanatory variables are ﬁxed, or because the

events that are being counted are positively correlated. Overdispersion typi-

cally arises because the events being counted arise in clusters or are mutually

supporting in some way. This causes the underlying events to be positively

correlated, and overdispersion of the counts is the result.

The presence of overdispersion might or might not aﬀect the parameter

estimates

, depending on the nature of the overdispersion, but the stan-

dard errors se(

) are necessarily underestimated. Consequently, tests on the

explanatory variables will generally appear to be more signiﬁcant that war-

ranted by the data, and conﬁdence intervals for the parameters will be nar-

rower than warranted by the data.

Overdispersion is detected by conducting a goodness-of-ﬁt test (as de-

scribed in Sect. 7.4). If the residual deviance and Pearson goodness-of-ﬁt

statistics are much larger than the residual degrees of freedom, then either

the ﬁtted model is inadequate or the data are overdispersed. If lack of ﬁt

remains even after ﬁtting the maximal possible explanatory model, and after

eliminating any outliers, then overdispersion is the alternative explanation.

When the counts are very small, so asymptotic approximations to the

residual deviance and Pearson statistics are suspect (Sect. 7.5,p.276), then

overdispersion may be diﬃcult to judge. However the goodness-of-ﬁt statistics

are more likely to be underestimated than overestimated in small count situ-

ations, so large goodness-of-ﬁt statistics should generally be taken to indicate

lack of ﬁt.

398 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.9 The number of membrane pock marks at various dilutions of the viral

medium (Example 10.9)

Dilution Pock counts

1 116 151 171 194 196 198 208 259

2 71 74 79 93 94 115 121 123 135 142

4 27333444495152596792

8 8 10 15 22 26 27 30 41 44 48

16 567789991120

Example 10.8. For the ﬁnal model ﬁtted to the kidney stone data (see

Table 10.6), the residual deviance was 3.5 and the residual df was 2. A

goodness-of-ﬁt test does not reject the hypothesis that the model is adequate:

> pchisq(deviance(ks.noMO), df.residual(ks.noMO), lower.tail=FALSE)

[1] 0.1781455



Example 10.9. In an experiment [35] to assess viral activity, pock marks were

counted at various dilutions of the viral medium (Table 10.9; data set: pock).

We use the logarithm to base 2 of Dilution as a covariate, since the dilution

levels are in increasing powers of 2 suggesting this was factored into the

design. A plot of the data shows a deﬁnite relationship between the variables

(Fig. 10.3, left panel), and that the variance increases with increasing mean

(Fig. 10.3, right panel):

> data(pock)

> plot( Count ~ jitter(log2(Dilution)), data=pock, las=1,

xlab="Log (base 2) of dilution", ylab="Pock mark count")

> mn <- with(pock, tapply(Count, log2(Dilution), mean) ) # Group means

> vr <- with(pock, tapply(Count, log2(Dilution), var) ) # Group variances

> plot( log(vr) ~ log(mn), las=1,

xlab="Group mean", ylab="Group variance")

Intuitively, pock marks are more likely to appear in clusters rather than

independently, so overdispersion would not be at all surprising. Indeed, the

sample variance is much larger than the mean for each group, clear evidence

of overdispersion:

> data.frame(mn, vr, ratio=vr/mn)

mn vr ratio

0 186.625 1781.12500 9.543871

1 104.700 667.34444 6.373872

2 50.800 360.40000 7.094488

3 27.100 194.98889 7.195162

4 9.100 17.65556 1.940171

10.5 Overdispersion 399

lll

01234

100

150

200

250

Log (base 2) of dilution

Pock mark count

2.5 3.5 4.5

Group mean

Group variance

Fig. 10.3 The pock data. Left panel, the counts against the logarithm of dilution; right

panel: the logarithm of the group variances against the logarithm of the group means

(Example 10.9)

Not only are the variances greater than the means, but their ratio increases

with the mean as well. The slope of the trend in the right panel of Fig. 10.3

is about 1.5:

> coef(lm(log(vr)~log(mn)))

(Intercept) log(mn)

0.02861162 1.44318666

This suggests a variance function approximately of the form V (μ)=μ

1.5

The mean–variance relationship here is in some sense intermediate between

that for the Poisson (V (μ)=μ) and gamma (V (μ)=μ

) distributions.

Fitting a Poisson glm shows substantial lack of ﬁt, as expected:

> m1 <- glm( Count ~ log2(Dilution), data=pock, family=poisson )

> X2 <- sum(residuals(m1, type="pearson")^2)

> c(Df=df.residual(m1), Resid.Dev=deviance(m1), Pearson.X2=X2)

Df Resid.Dev Pearson.X2

46.0000 290.4387 291.5915

The saddlepoint approximation is satisfactory here as min{y

} = 5 is greater

than 3. Indeed, the deviance and Pearson goodness-of-ﬁt statistics are nearly

identical. Two ways to model the overdispersion are discussed in Sects. 10.5.2

and 10.5.3. 

10.5.2 Negative Binomial GLMs

One way to model overdispersion is through a hierarchical model. Instead of

assuming y

∼ Pois(μ

), we can add a second layer of variability by allowing

itself to be a random variable. Suppose instead that

|λ

∼ Pois(λ

)andλ

∼ G(μ

,ψ)

400 10 Models for Counts: Poisson and Negative Binomial GLMs

where G(μ

,ψ) denotes a distribution with mean μ

and coeﬃcient of vari-

ation ψ. For example, we could imagine that the number of pock marks

recorded in the pock data (Example 10.9) might follow a Poisson distribu-

tion for any given viral concentration, but that the viral concentration varies

somewhat between replicates for any given dilution with a coeﬃcient of vari-

ation ψ. It is straightforward to show, under the hierarchical model, that

E[y

]=μ

and var[y

]=μ

+ ψμ

so the variance contains an overdisperion term ψμ

. The larger ψ, the greater

the overdispersion.

A popular choice is to assume that the mixing distribution G is a gamma

distribution. The coeﬃcient of variation of a gamma distribution is its dis-

persion parameter, so the second layer of the hierachical model becomes

∼ Gam(μ

,ψ). With this assumption, is it possible to show that y

follows

a negative binomial distribution with probability function

P(y

; μ

,k)=

Γ (y

+ k)

Γ (y

+1)Γ (k)



+ k





1 −

+ k



, (10.11)

where k =1/ψ and Γ () is the gamma function, so that var[y

]=μ

+ μ

/k.

For any ﬁxed value of k, it can be shown (Problem 10.1) that the negative

binomial distribution is an edm with unit deviance

d(y, μ)=2



y log

− (y + k) log

y + k

μ + k



where the limit form (5.14)isusedify = 0. Hence the negative binomial

distribution can be used to deﬁne a glm for any given k. Note that negative

binomial edms have dispersion φ =1,asdoalledms for count data, because

var[y

] is determined by μ

and k. In practice, k is rarely known and so

negative binomial glms are usually used with an estimated value for k.Inr,

the function glm.nb() from package MASS canbeusedinplaceofglm()

to ﬁt the model. The function glm.nb() undertakes maximum likelihood

estimation for both k and the glm coeﬃcients β

simultaneously (see ?glm.

nb).

The estimation of k introduces an extra layer of uncertainty into a negative

binomial glm. However the maximum likelihood estimator

k of k is uncorre-

lated with the

, according to the usual asymptotical approximations. Hence

the glm ﬁt tends to be relatively stable with respect to estimation of k.

Negative binomial glms give larger standard errors than the correspond-

ing Poisson glms, depending on the size of k =1/ψ. On the other hand, the

coeﬃcient estimates

from a negative binomial glm may be similar to those

produced from the corresponding Poisson glm. The negative binomial glm

gives less weight to observations with large μ

than does the Poisson glm,

and relatively more weight to observations with small μ

, so the coeﬃcients

10.5 Overdispersion 401

will vary somewhat. Unlike glm(), where the default link function for every

family is the canonical link, the default link function for glm.nb() is the

logarithmic link function. Indeed the log-link is almost always used with neg-

ative binomial glms to ensure μ>0 for any value of the linear predictor. The

function glm.nb() also allows the "sqrt" and "identity" link functions.

For negative binomial glms, the use of quantile residuals [12] is strongly

recommended (Sect. 8.3.4.2).

Example 10.10. The pock data shows overdispersion (Example 10.9; data set:

pock). We ﬁt a negative binomial glm, estimating k using the function glm.

nb() in package MASS (note that glm.nb() uses theta to denote k):

> library(MASS) # Provides the function glm.nb()

> m.nb <- glm.nb( Count ~ log2(Dilution), data=pock )

> m.nb$theta # This is the value of k (called theta in MASS)

[1] 9.892894

The output object m.nb includes information about the estimation of k.The

output from glm.nb() model is converted to the style of output from glm()

using glm.convert():

> m.nb <- glm.convert(m.nb)

> printCoefmat(coef(summary(m.nb, dispersion=1)))

Estimate Std. Error z value Pr(>|z|)

(Intercept) 5.33284 0.08786 60.697 < 2.2e-16 ***

log2(Dilution) -0.72460 0.03886 -18.646 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Note that we have to specify explicitly that the dispersion parameter is φ =1,

because after using glm.convert(), r does not know automatically that the

resulting glm family should have dispersion equal to one.

Since k ≈ 10, the negative binomial model is using the variance function

V (μ) ≈ μ + μ

/10. The coeﬃcient of variation of the mixing distribution

(ψ =1/k) is estimated to be about 10%, a reasonable level for replicate

to replicate variation. Comparing the Poisson and negative binomial models

shows that the parameter estimates are reasonably close, but the standard

errors are quite diﬀerent:

> printCoefmat( coef( summary(m1)) ) # Poisson glm information

Estimate Std. Error z value Pr(>|z|)

(Intercept) 5.2679 0.0226 233.6 <2e-16 ***

log2(Dilution) -0.6809 0.0154 -44.1 <2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The diagnostic plots (Fig. 10.4, top panels) suggest the negative binomial

model is adequate. No observations are particularly inﬂuential. 

402 10 Models for Counts: Poisson and Negative Binomial GLMs

lll

50 100 150 200

−2

−1

Negative binomial

Fitted values

Standardized residuals

lll

50 100 150 200

−2

−1

Quasi−Poisson

Fitted values

Standardized residuals

−2 −1 0 1 2

−2

−1

Normal Q−Q plot

Quantile residuals

Theoretical Quantiles

Sample Quantiles

lll

−2 −1 0 1 2

−2

−1

Normal Q−Q plot

Standardized residuals

Theoretical Quantiles

Sample Quantiles

010203040

0.00

0.02

0.04

0.06

0.08

0.10

0.12

Negative binomial:

Cook's distance

Index

Cook's distance, D

010203040

0.00

0.05

0.10

0.15

0.20

0.25

0.30

Quasi−Poisson:

Cook's distance

Index

Cook's distance, D

Fig. 10.4 Diagnostic plots from ﬁtting the negative binomial model (top panels) and

the quasi-Poisson models (bottom panels) to the pock data (Example 10.9)

10.5.3 Quasi-Poisson Models

The simplest to use, and therefore most commonly used, approach to overdis-

persed counts are quasi-Poisson models. Quasi-Poisson models keep the Pois-

son variance function V (μ)=μ but simply allow a general positive dispersion

parameter φ,sothatvar[y

]=φμ

. Here φ>1 corresponds to overdispersion.

This approach can be motivated in the same way as were quasi-binomial mod-

els (Sect. 9.8). Suppose that the counts y

are counts of cases arising from a

large population of size N, and the suppose that the individuals in the pop-

ulation are positively correlated. Then E[y

]=μ

= Nπ

, where π

is the

probability that a random individual is a case, and var[y

]=φNπ

(1 − π

)

where φ =1+(N − 1)ρ and ρ is the correlation between individuals. If N is

large and the π

are small, then var[y

] ≈ φNπ

= φμ

When φ = 1, there is no edm with this variance function that gives positive

probability to integer values of y

. Nevertheless, the quasi-likelihood methods

of Sect. 8.10 still apply, so quasi-Poisson glms yield consistent estimators and

10.5 Overdispersion 403

consistent standard errors for the β

, provided only that E[y

]andvar[y

]are

correctly speciﬁed. Note that quasi-Poisson glms reduce to Poisson glms

when φ =1.

The coeﬃcient estimates from a quasi-Poisson glm are identical to those

from the corresponding Poisson glm (since the estimates

do not depend

on φ), but the standard errors are inﬂated by a factor of

√

φ. Conﬁdence

intervals and statistics for testing hypotheses tests will change for the same

reason.

Note that quasi-Poisson and the negative binomial model both produce

overdispersion relative to the Poisson distribution but they assume diﬀerent

mean–variance relationships. Quasi-Poisson models assume a linear variance

function (V (μ)=φμ) whereas negative binomial models uses a quadratic

variance function (V (μ)=μ + μ

/k).

Quasi-Poisson models are ﬁtted in r using glm() and specifying family=

quasipoisson().Asforfamily=poisson(), the default link function is the

"log" link, while "identity" and "sqrt" are also permitted. Since the quasi-

Poisson model is not based on a probability model, the aic is undeﬁned. For

the same reason, quantile residuals [12] cannot be computed for the quasi-

Poisson glm since no probability model is deﬁned.

Example 10.11. The model ﬁtted to the pock data shows overdispersion (Ex-

ample 10.9), so an alternative solution is to ﬁt a quasi-Poisson model:

> m.qp <- glm( Count ~ log2(Dilution), data=pock, family="quasipoisson")

The diagnostic plots (Fig. 10.4, bottom panels) suggest the quasi-Poisson

model is broadly adequate, and no observations are particularly inﬂuential.

It is discernible from the left panels of Fig. 10.4, however, that the negative

binomial model tends to under-estimate slightly the variances of the low

counts while the quasi-Poisson model does the same for large counts.

F -tests are used for model comparisons, since φ is estimated. Comparing

the standard errors from the quasi-Poisson model to the standard errors

produced from the Poisson glm, the standard errors in the quasi-Poisson

model are scaled by



φ :

> se.m1 <- coef(summary(m1))[, "Std. Error"]

> se.qp <- coef(summary(m.qp))[, "Std. Error"]

> data.frame(SE.Pois=se.m1, SE.Quasi=se.qp, ratio=se.qp/se.m1)

SE.Pois SE.Quasi ratio

(Intercept) 0.02255150 0.05677867 2.517733

log2(Dilution) 0.01544348 0.03888257 2.517733

> sqrt(summary(m.qp)$dispersion)

[1] 2.517733

Note that quantile residuals can be produced for the negative binomial glm

since a full probability function is deﬁned, but quantile residuals cannot be

computed for the quasi-Poisson glm since no probability model is deﬁned.

For this reason, the residual plots for the quasi-Poisson model use standard-

ized deviance residuals. The ﬁtted systematic components are compared in

404 10 Models for Counts: Poisson and Negative Binomial GLMs

lll

01234

100

150

200

250

Poisson

log2(Dilution)

Count

lll

01234

100

150

200

250

Negative binomial

log2(Dilution)

Count

lll

01234

100

150

200

250

Quasi−Poisson

log2(Dilution)

Count

Fig. 10.5 Models ﬁtted to the pock data, including the 99.9% conﬁdence intervals for

ˆμ (Example 10.11)

Fig. 10.5. Recall the Poisson and quasi-Poisson models produce identical pa-

rameter estimates, and hence ﬁtted values.

> coef.mat <- rbind( coef(m1), coef(m.qp), coef(m.nb) )

> rownames(coef.mat) <- c("Poisson glm", "Quasi-Poisson", "Neg bin glm")

> coef.mat

(Intercept) log2(Dilution)

Poisson glm 5.267932 -0.6809442

Quasi-Poisson 5.267932 -0.6809442

Neg bin glm 5.332844 -0.7245983

The plots in Fig. 10.5 show that the diﬀerent approaches model the random-

ness diﬀerently.

We can now interpret the ﬁtted model. The ﬁtted models say that the

expected number of pock marks decreased by a factor of about exp(−0.7) ≈

0.5 for every 2-fold dilution. In other words, the expected number of pock

marks is directly proportional to the concentration of the viral medium. 

10.6 Case Study

In a study of nesting female horseshoe crabs [1, 5], each with an attached

male, the number of other nearby male crabs (called satellites) were counted

(Table 10.10; data set: hcrabs). The colour of the female, the condition of her

spine, her carapace width, and her weight were also recorded. The purpose of

the study is to understand the factors that attract satellite crabs. Are they

more attracted to larger females? Does the condition or colour of the female

play a role?

10.6 Case Study 405

Table 10.10 The horseshoe crab data (Example 10.6)

Spine Carapace Number of Weight

Colour condition width (in cm) satellites (in g)

Medium None OK 28.3 8 3050

Dark medium None OK 22.5 0 1550

Light medium Both OK 26.0 9 2300

Dark medium None OK 24.8 0 2100

Dark medium None OK 26.0 4 2600

Medium None OK 23.8 0 2100

Colour is on a continuum from light to dark, and spine condition counts

the number of intact sides, so we deﬁne both as ordered factors:

> data(hcrabs); str(hcrabs)

'data.frame': 173 obs. of 5 variables:

$ Col : Factor w/ 4 levels "D","DM","LM",..: 4232243242...

$ Spine: Factor w/ 3 levels "BothOK","NoneOK",..: 2212221312...

$ Width: num 28.3 22.5 26 24.8 26 23.8 26.5 24.7 23.7 25.6 ...

$Sat :int 8090400000...

$ Wt : int 3050 1550 2300 2100 2600 2100 2350 1900 1950 2150 ...

> hcrabs$Col <- ordered(hcrabs$Col, levels=c("LM", "M", "DM", "D"))

> hcrabs$Spine <- ordered(hcrabs$Spine,

levels=c("NoneOK", "OneOK", "BothOK"))

Plotting Sat against the other variables shows trends for more satellite crabs

to congregate around females that are larger (in weight and width), are lighter

in colour, and have no spinal damage (Fig. 10.6).

> with(hcrabs,{

logSat <- log(Sat+1)

plot( jitter(Sat) ~ Wt, ylab="Sat", las=1)

plot( jitter(logSat) ~ log(Wt), ylab="log(Sat+1)", las=1)

plot( logSat ~ Col, ylab="log(Sat+1)", las=1)

plot( jitter(Sat) ~ Width, ylab="Sat", las=1)

plot( jitter(logSat) ~ log(Width), ylab="log(Sat+1)", las=1)

plot( logSat ~ Spine, ylab="log(Sat+1)", las=1)

})

jitter() is used to avoid overplotting. Plots on the log-scale are preferable

because the values of Wt and Width are distributed more symmetrically on

the log-scale, and because the relationships between them and Sat are more

likely to be relative rather than additive. log(Sat+1) is used to avoid taking

logarithm of zero.

406 10 Models for Counts: Poisson and Negative Binomial GLMs

2000 4000

Sat

7.5 8.0 8.5

0.0

0.5

1.0

1.5

2.0

2.5

log(Wt)

log(Sat+1)

LM M DM D

0.0

0.5

1.0

1.5

2.0

2.5

Col

log(Sat+1)

22 26 30 34

Width

Sat

3.1 3.2 3.3 3.4 3.5

0.0

0.5

1.0

1.5

2.0

2.5

log(Width)

log(Sat+1)

NoneOK BothOK

0.0

0.5

1.0

1.5

2.0

2.5

Spine

log(Sat+1)

Fig. 10.6 The number of satellites on each female horseshoe crab plotted against the

weight, colour, width and spine condition (Sect. 10.6)

3.1 3.2 3.3 3.4 3.5

7.5

8.0

8.5

log(Width)

log(Wt)

LM M DM D

7.5

8.0

8.5

Col

log(Wt)

NoneOK BothOK

7.5

8.0

8.5

Spine

log(Wt)

Fig. 10.7 Weight of each female horseshoe crab plotted against width, colour and spine

condition (Sect. 10.6)

The explanatory variables are inter-related however; Wt is the most obvious

overall summary of the size of each female. It turns out that lighter-coloured

females are also typically heavier, as are females with no spine damage, so the

relationships observed between Sat and Col and Spine might be explained

by this (Fig. 10.7).

10.6 Case Study 407

> with(hcrabs,{

plot( log(Wt) ~ log(Width), las=1 )

plot( log(Wt) ~ Col, las=1 )

plot( log(Wt) ~ Spine, las=1 )

})

> coef(lm( log(Wt) ~ log(Width), data=hcrabs ))

(Intercept) log(Width)

-0.60 2.56

Wt should be proportional to the volume of each female, hence should be

approximately proportional to Width^3, if the females are all the same shape.

Indeed, log(Wt) is nearly linearly related to log(Width) with a slope nearly

equal to 3.

Crabs tend to congregate and interact with one another, rather than be-

having independently, hence we should expect overdispersion a priori relative

to Poisson for the counts of satellite crabs. We ﬁt a quasi-Poisson glm with

log-link:

> cr.m1 <- glm(Sat ~ log(Wt) + log(Width) + Spine + Col,

family=quasipoisson, data=hcrabs)

> anova(cr.m1, test="F")

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 172 633

log(Wt) 1 83.1 171 550 25.96 9.4e-07 ***

log(Width) 1 0.0 170 550 0.00 0.96

Spine 2 1.1 168 549 0.18 0.84

Col 3 7.6 165 541 0.79 0.50

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

> deviance(cr.m1)

[1] 541

> df.residual(cr.m1)

[1] 165

The residual deviance and Pearson X

are both more than three times the

residual degrees of freedom, so our expectation of overdispersion seems con-

ﬁrmed. Using F -tests, log(Wt) is a highly signiﬁcant predictor whereas none

of the other variables are at all signiﬁcant, after adjusting for log(Wt).We

adopt a model with just Wt as an explanatory variable:

> cr.m2 <- glm(Sat ~ log(Wt), family=quasipoisson, data=hcrabs)

> printCoefmat(coef(summary(cr.m2)), digits=3)

Estimate Std. Error t value Pr(>|t|)

(Intercept) -12.568 2.664 -4.72 4.9e-06 ***

log(Wt) 1.744 0.339 5.15 7.0e-07 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

It is tempting to speculate on the biological implications. It might well

be possible for a male crab to sense the overall weight of the female crab by

smell or other chemical senses, because the amount of chemical emitted by

408 10 Models for Counts: Poisson and Negative Binomial GLMs

a female should be proportional to her size, whereas width, colour or spine

damage would need vision. The results perhaps suggest that the crabs do not

use vision as their primary sense.

We may worry that nearly half of the values of the response Sat are 0 or

1, which may suggest a problem for the distribution of the residual deviance

and the evaluation of overdispersion. However a quick simulation shows that

the chi-square approximation for the residual deviance is excellent:

> x <- log(hcrabs$Wt); dev <- rep(NA, 100)

> n <- length(hcrabs$Sat); mu <- fitted(cr.m2)

> for (i in 1:100) {

y <- rpois(n, lambda=mu) # Generate random Poisson values

dev[i] <- glm(y~x, family=quasipoisson)$deviance

}

> c(Mean.Dev=mean(dev), Std.Dev=sd(dev))

Mean.Dev Std.Dev

185.53962 19.61709

The mean and standard deviance of the residual deviance are close to their

theoretical values of df = 171 and

√

2 × df = 18.5 respectively, under the null

hypothesis of Poisson variation. (Note: A χ

distribution with k degrees of

freedom has mean k and standard deviation

√

2k.)

The diagnostics for this model suggest a reasonable model:

> plot( resid(cr.m2) ~ sqrt(fitted(cr.m2)), las=1,

main="Deviance residuals", ylab="Deviance residuals",

xlab="Square root of fitted values" )

> plot( cooks.distance(cr.m2), type="h", las=1,

ylab="Cook's distance, D", main="Cook's distance")

> qqnorm( resid(cr.m2), las=1,

main="Normal Q-Q plot\ndeviance residuals")

> qqline( resid(cr.m2))

Notice that quantile residuals cannot be used for the quasi-Poisson model; the

trend in the bottom left of the Q–Q plot may be due to the use of deviance

residuals (Fig. 10.8). No observation is identiﬁed as inﬂuential using Cook’s

distance or dfbetas, but other criteria indicate inﬂuential observations:

> colSums( influence.measures(cr.m2)$is.inf )

dfb.1_ dfb.l(W) dffit cov.r cook.d hat

001803

The quasi-Poisson model indicates that heavier crabs have more satellites

on average. The ﬁtted systematic component is

log μ = −12.57 + 1.744 log W or equivalently μ =0.000003483 × W

1.744

where W is the weight of the crabs in grams. If the regression coeﬃcient for

log W was 1, then the expected number of satellite crabs would be directly

proportional to the weight of the female. The number of satellites seems to

increase just a little faster than this.

10.6 Case Study 409

1.0 1.5 2.0 2.5 3.0

−2

Deviance residuals

Square root of fitted values

Deviance residuals

0 50 100 150

0.00

0.01

0.02

0.03

0.04

0.05

0.06

Cook's distance

Index

Cook's distance, D

−2 −1 0 1 2

−2

Normal Q−Q plot

deviance residuals

Theoretical Quantiles

Sample Quantiles

Fig. 10.8 Diagnostic plots for the quasi-Poisson model cr.m2. The deviance residuals

against ﬁtted values (left panel); Cook’s distance (centre panel); a Q–Q plot of the

quantile residuals (right panel) (Sect. 10.6)

An alternative model is to ﬁt a negative binomial model:

> library(MASS)

> cr.nb <- glm.nb(Sat ~ log(Wt), data=hcrabs)

> cr.nb <- glm.convert(cr.nb)

> anova(cr.nb, dispersion=1, test="Chisq")

Df Deviance Resid. Df Resid. Dev Pr(>Chi)

NULL 172 219.81

log(Wt) 1 23.339 171 196.47 1.358e-06 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

> printCoefmat(coef(summary(cr.nb, dispersion=1)))

Estimate Std. Error z value Pr(>|z|)

(Intercept) -14.55581 3.10909 -4.6817 2.845e-06 ***

log(Wt) 1.99862 0.39839 5.0168 5.254e-07 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

> cr.nb$theta

[1] 0.9580286

The ﬁtted negative binomial distribution uses

k =0.9580. The diagnostic

plots (not shown) indicate that the negative binomial model is also suitable.

No observation is identiﬁed as inﬂuential using Cook’s distance:

> colSums( influence.measures(cr.nb)$is.inf )

dfb.1_ dfb.l(W) dffit cov.r cook.d hat

000603

410 10 Models for Counts: Poisson and Negative Binomial GLMs

lllllll

lll

llll

ll llll

llll

lll

7.5 8.0 8.5

Fitted models

log(Wt)

Sat

Quasi−poisson

Neg. binomial

lllllll

lll

llll

ll llll

llll

lll

7.5 8.0 8.5

CIs for fitted values

log(Wt)

Sat

Quasi−poisson

Neg. binomial

Fig. 10.9 Comparing the systematic components of the quasi-Poisson model and the

negative binomial glm (left panel) and the corresponding 95% conﬁdence intervals (right

panel) ﬁtted to the horseshoe crab data. Solid lines represent the quasi-Poisson model,

while dashed lines represent the negative binomial model

The diﬀerences between the two models becomes apparent for heavier

crabs, for both the systematic components (Fig. 10.9, left panel) and the

random components (Fig. 10.9, right panel). First, create predictions for a

range of weights:

> newW <- seq( min(hcrabs$Wt), max(hcrabs$Wt), length=100)

> newS.qp <- predict(cr.m2, newdata=data.frame(Wt=newW), se.fit=TRUE)

> newS.nb <- predict(cr.nb, newdata=data.frame(Wt=newW), se.fit=TRUE,

dispersion=1)

> tstar <- qt(0.975, df=df.residual(cr.m2) ) # For a 95% CI

> ME.qp <- tstar * newS.qp$se.fit; ME.nb <- tstar * newS.nb$se.fit

> mu.qp <- newS.qp$fit; mu.nb <- newS.nb$fit

Then plot:

> par( mfrow=c(1, 2))

> plot( Sat~log(Wt), data=hcrabs, las=1, main="Fitted models")

> lines( exp(mu.qp) ~ log(newW), lwd=2 )

> lines( exp(mu.nb) ~ log(newW), lwd=2, lty=2 );

> legend("topleft", lty=1:2, legend=c("Quasi-poisson", "Neg. binomial") )

> plot( Sat~log(Wt), data=hcrabs, las=1, main="CIs for fitted values")

> ci.lo <- exp(mu.qp - ME.qp); ci.hi <- exp(mu.qp + ME.qp)

> lines( ci.lo ~ log(newW), lwd=2); lines( ci.hi ~ log(newW), lwd=2)

> ci.lo <- exp(mu.nb - ME.nb); ci.hi <- exp(mu.nb + ME.nb)

> lines( ci.lo ~ log(newW), lwd=2, lty=2)

> lines( ci.hi ~ log(newW), lwd=2, lty=2)

> legend("topleft", lty=1:2, legend=c("Quasi-poisson", "Neg. binomial") )

10.8 Summary 411

10.7 Using R to Fit GLMs to Count Data

A Poisson glm is speciﬁed in r using glm(formula, family=poisson())

(note the lower case p). The link functions "log", "identity",and"sqrt"

are permitted with Poisson distributions. Quasi-Poisson models are speciﬁed

using glm(formula, family=quasipoisson()).

To ﬁt negative binomial models, use glm.nb() from package MASS [37]

when k is unknown (the usual situation). The output from glm.nb() is con-

verted to the style of output from glm() using glm.convert(). Then, the

usual anova() and summary() commands may be used, remembering to set

dispersion=1 when using summary(). See ?negative.binomial, ?glm.nb,

and Sect. 10.5.2 for more information.

The function gl() is useful for generating factors occurring in a regular

pattern, as is common in tabulated data. gl(3, 2, 12) produces a factor of

length 12 with three levels (labelled 1, 2 and 3 by default), appearing two at

a time:

> gl(3, 2, 18, labels=c("A", "B", "C") )

[1]AABBCCAABBCCAABBCC

Levels:ABC

The functions margin.table() and prop.table() are useful for produc-

ing marginal tables and tables of proportions from raw data in tables

(Sect. 10.4.5).

10.8 Summary

Chapter 10 considers ﬁtting glms to count data. Counts are commonly mod-

elled using the Poisson distribution (Sect. 10.2), where μ>0 is the expected

count and y =0, 1, 2,.... Note that φ =1andV (μ)=μ. The residual dev-

iance D(y, ˆμ) is suitably described by a χ

n−p



distribution if min{y

}≥3

(Sect. 10.2). The logarithmic link function is often used for Poisson glms

(Sect. 10.2).

When any of the explanatory variables are quantitative, the ﬁtted Poisson

glm is also called a Poisson regression model. When all the explanatory

variables are qualitative, the ﬁtted Poisson glm is also called a log-linear

model (Sect. 10.2).

Poisson glms can be used to model rates (such as counts of cancer cases

per unit of population) by using a suitable oﬀset in the linear predictor

(Sect. 10.3).

Count data often appear cross-classiﬁed in tables, commonly called con-

tingency tables (Sect. 10.4). Contingency tables may arise under various sam-

pling schemes, each implying a diﬀerent random component (Sect. 10.4). How-

412 10 Models for Counts: Poisson and Negative Binomial GLMs

ever, in all cases a Poisson glm can be ﬁtted provided the coeﬃcients in the

linear predictor corresponding to ﬁxed margins are included in the model.

Three-dimensional tables may be interpreted, and possibly simpliﬁed, ac-

cording to which interactions are present in the model (Sect. 10.4.4). If tables

are collapsed incorrectly, the resulting tables may be misleading. Simpson’s

paradox is an extreme example (Sect. 10.4.5). Poisson glms ﬁtted to higher-

order tables may be diﬃcult to interpret (Sect. 10.4.7).

Contingency tables may contain cells with zero counts (Sect. 10.4.8). Sam-

pling zeros occur by chance, and larger samples may produce counts in these

cells. Structural zeros appear for impossible events, so cells containing struc-

tural zeros must be removed from the analysis.

Overdispersion occurs when the variation in the responses is greater than

expected under the Poisson model (Sect. 10.5). Possible causes are that the

model is misspeciﬁed (in which case the model should be amended), the

means are not constant, or the responses are not independent.

In cases of overdispersion relative to the Poisson glm, a negative bino-

mial distribution may be used, which is an edm if k is known (Sect. 10.5.2).

For the negative binomial distribution, V (μ)=μ + μ

/k for k>0. The

value of k usually needs to be estimated (by

k) for a negative binomial glm

(Sect. 10.5.2). If overdispersion is observed, a quasi-Poisson model may be

ﬁtted also, which assumes V (μ)=φμ (Sect. 10.5.3).

Problems

Selected solutions begin on p. 541.

10.1. Consider the negative binomial distribution, whose probability function

is given in (10.11).

1. Show that the negative binomial distribution with known k is an edm,

by identifying θ, κ(θ)andφ. (See Sect. 5.3.6,p.217.)

2. Show that the negative binomial distribution with known k has var[y]=

μ + μ

/k.

3. Deduce the canonical link function for the negative binomial distribution.

4. Show that, for the negative binomial distribution,

d(y, μ)=2



y log

− (y + k) log

y + k

μ + k



for y>0. Also, deduce the unit deviance when y =0.

10.2. If the ﬁtted Poisson glm includes a constant term, and the logarithmic

link function is used, the sum over the observations of the second term in the

expression for the residual deviance is zero. In other words,



i=1

− ˆμ

0. Prove this result by writing the log-likelihood for a model with linear

10.8 Summary 413

predictor containing a constant term, say β

, diﬀerentiating the log-likelihood

with respect to β

, setting to zero, and solving.

10.3. Sometimes, count data explicitly omit zero counts. Examples include

the numbers of days patients spend in hospital (only patients who actually

stay overnight in hospital are considered, and so the smallest possible count

is one); the number of people per car using a rural road (the driver at least

must be in the car); and a survey of the number of people living in each

household (to respond, the households must have at least one person). Using

a Poisson distribution is inadequate, as the zero counts will be modelled as

true zero counts.

In these situations, the zero-truncated Poisson distribution may be suit-

able, with probability function

P(y; λ)=

exp(−λ)λ

{1 − exp(−λ)}y!

where y =1, 2,... and λ>0.

1. Show that the truncated Poisson distribution is an edm by identifying θ

and κ(θ).

2. Show that μ =E[y]=λ/{1 − exp(−λ)}, and that μ>1.

3. Find the variance function for the truncated Poisson distribution.

4. Plot the truncated Poisson distribution and the Poisson distribution for

λ = 2, and compare.

10.4. A study [25] used a Poisson glm to model the number of politicians

switching political parties in the usa. The response variable was the number

of members of the House of Representatives who switched parties every year

from 1802–1876.

1. Explain why the authors used a Poisson glm to model the data.

2. The authors use eleven possible explanatory variables in the linear pre-

dictor. One of the explanatory variables is whether or not the year is an

election year (election years are coded as 0, non-election years as 1). The

coeﬃcient for this explanatory variable is 1.051. Interpret the meaning of

this coeﬃcient.

3. The estimated standard error for the election year parameter is 0.320.

Determine if the parameter is statistically signiﬁcant.

4. Compute and interpret a 90% conﬁdence interval for the election year

parameter.

10.5. A study in the usa [22] examined the number of pregnancies in a

stratiﬁed random sample of 1154 sexually-active teenage girls (7th to 12th

grade). Details of the ﬁtted Poisson glm are shown in Table 10.11.

1. Explain why the years of sexual activity is used as an oﬀset.

414 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.11 The ﬁtted Poisson glms for the teenage pregnancy data. The response

variable is the number of pregnancies. All variables are binary (0: no; 1: yes) apart from

age, which is measured in completed years. Years of sexual activity is used as an oﬀset

(Problem 10.5)

Wald 95%

se(

) conﬁdence limits Deviance

Intercept 1 −2.0420 0.9607 −3.9248 −0.1591 4.52

Current age (in years) 1 0.1220 0.0543 0.0156 0.2283 5.05

Race (‘White’ is the reference)

African-American 1 0.6604 0.1287 0.4082 0.9126 26.33

Hispanic 1 0.2070 0.2186 −0.2215 0.6354 0.90

Asian 1 0.4896 0.3294 −0.1561 1.1352 2.21

Single 1 −0.9294 0.2080 −1.3371 −0.5218 19.97

College plans 1 −0.0871 0.0515 −0.1881 0.0139 2.86

Contraceptive self-eﬃcacy 1 −0

.2241 0.0845 −0.3897 −0.0585 7.04

Consistent use of contraceptives 1 −0.2729 0.0825 −0.4346 −0.1113 10.95

Residual df: 1144

Residual deviance: 3359.9

2. Use likelihood ratio tests to identify statistically signiﬁcant explanatory

variables.

3. Use the Wald statistics to identify statistically signiﬁcant explanatory

variables. Compare to the results of using the likelihood ratio test.

4. Interpret the coeﬃcients in the model.

5. Show that overdispersion may be present.

6. Because of the possible overdispersion, estimate φ for the quasi-Poisson

model. Hence compute

and se(

) for the quasi-Poisson glm.

7. Form a 95% conﬁdence interval for age using the quasi-Poisson glm.

10.6. The brood sizes of blue tits were experimentally changed (increased

or decreased) through three brooding seasons to study the survival of oﬀ-

spring [32, Table 2]. The hypothesis was that blue tits should produce the

clutch size maximizing the survival of their oﬀspring (so that manipulated

broods should show less surviving oﬀspring than unmanipulated broods). In

other words, the number of eggs laid is optimum given the ability of the par-

ents to rear the oﬀspring (based on their body condition, food resources, age,

etc.). A log-linear model for modelling the number of oﬀspring surviving y

produced the results in Table 10.12, where M is the amount of manipulation

(ranging from taking ten eggs (M = −10) to adding four eggs (M =4)to

the clutch), and C is the original clutch size (ranging from two to 17 eggs).

1. Write down the ﬁtted model from Table 10.12 (where

= −2.928).

2. Using likelihood ratio tests, determine which explanatory variables are

signiﬁcant.

3. Use Wald statistics to determine the signiﬁcance of each parameter. Com-

pare to the results from the likelihood ratio tests, and comment.

10.8 Summary 415

Table 10.12 The analysis of deviance table for a Poisson glm ﬁtted to the blue tits

data. The response variable is the number of oﬀspring surviving (Problem 10.6)

Model Residual deviance df

se(

)

Null model 732.74 617

+ C 662.25 616 0.238 0.028

+ M 649.01 615 0.017 0.035

+ M

637.22 614 −0.028 0.009

Table 10.13 Information about the ﬁtted Poisson glm for the spina biﬁda study. The

response variable is the number of babies born with spina biﬁda (Problem 10.7)

Model Residual deviance df

se(

)

Null 554.11 200

+logB 349.28 199 1.06 0.07

+ S 305.32 197 −8.61 0.68 (routine screening)

−8.18 0.67 (no routine screening)

−8.43 0.68 (policy uncertain)

+ C 285.06 196 −0.11 0.03

+ U 266.88 195 0.046 0.009

+ A 256.03 194 0.039 0.011

4. Compute and interpret the 95% conﬁdence interval for the eﬀect of the

original clutch size C.

5. Comment on under- or overdispersion for this model.

6. Using the ﬁtted model, determine the value of M maximizing expected

oﬀspring survival μ.

7. Determine if any manipulation of the clutch size decreases the survival

chances of the young.

10.7. A study of spina biﬁda in England and Wales [27] examined the rela-

tionship between the number of babies born with spina biﬁda between 1983

and 1985 inclusive in various Regional Health Authorities (rha), and explana-

tory variables such as the total number of live and still births between 1983–

1985, B; the screening policy of the health authority in 1982, S (routine; non-

routine; uncertain); the percentage of female residents born in the Caribbean,

C; the percentage economically-active residents unemployed, U ; the percent-

age of residents lacking a car, L; and the percentage of economically-active

residents employed in agriculture, A. A Poisson glm with a log-link was ﬁtted

(Table 10.13) to model the number of babies born with spina biﬁda.

1. Write down the ﬁtted model. (Note that a diﬀerent constant term is ﬁtted

for each screening policy.)

2. Using the standard errors, check which parameters are signiﬁcantly dif-

ferent from zero.

3. Use likelihood ratio tests to determine which explanatory variables are

signiﬁcant in the model.

416 10 Models for Counts: Poisson and Negative Binomial GLMs

4. Interpret the eﬀect of the unemployment rate U.

5. Compute and interpret the 95% conﬁdence interval for the eﬀect of the

unemployment rate U.

6. Explain why using log B as an oﬀset seems reasonable from the descrip-

tion of the data. Also explain why Table 10.13 supports this approach.

7. Is overdispersion likely to be a problem?

10.8. For the depressed youth data used in Sect. 10.4.7 (p. 393), ﬁt the model

used in that section as follows (data set: dyouth).

1. Show that the four-factor interaction is not signiﬁcant.

2. Show that only one three-factor interaction is signiﬁcant in the model.

3. Then show that four two-factor interactions are needed in the model

(some because they are signiﬁcant, some because of the marginality prin-

ciple).

4. Show that the model is adequate by examining the model diagnostics.

10.9. Consider the Danish lung cancer data of Example 10.1 (data set:

danishlc). In that example, a Poisson glm was ﬁtted to model the num-

ber of lung cancers per unit of population.

1. Fit a model for the proportion of lung cancers, based on the propor-

tion Cases/Pop, and compare to the equivalent Poisson glm ﬁtted in

Sect. 10.3.

2. Show that the conditions for the equivalence of the binomial and Poisson

glms, as given in Sect. 10.4.6, are approximately satisﬁed.

10.10. In Sect. 8.12 (p. 322), a Poisson glm was ﬁtted to the noisy miner

data [30] (data set: nminer) that was ﬁrst introduced in Example 1.5 (p. 14).

In Example 1.5, the only explanatory variable considered was the number

of eucalypts Eucs, but the data frame actually contains a number of other

explanatory variables: the number of buloke trees (Bulokes); the area in

hectares of remnant patch vegetation at each site (Area); whether the area

was grazed (Grazed: 1 means yes); and whether shrubs were present in the

transect (Shrubs: 1 means yes).

1. Find a suitable Poisson regression model for modelling the number of

noisy miners Minerab, including a diagnostic analysis.

2. Is the saddlepoint approximation likely to be accurate? Explain.

10.11. The number of deaths for 1969–1973 (1969–1972 for Belgium) due to

cervical cancer is tabulated (Table 10.14; data set: cervical) by age group

for four diﬀerent countries [19, 38].

1. Plot the data, and discuss any prominent features.

2. Explain why an oﬀset is useful when ﬁtting a glm to the data.

3. Fit a Poisson glm with Age and Country as explanatory variables. Pro-

duce the plot of residuals against ﬁtted values, and evaluated the model.

10.8 Summary 417

Table 10.14 The number of deaths y due to cervical cancer and woman-years at-risk

T in various age groups, for four countries (Problem 10.11)

25–34 35–44 45–54 55–64

Country yTyTyTyT

England and Wales 192 15,399 860 14,268 2762 15,450 3035 15,142

Belgium 8 2328 81 2557 242 2268 268 2253

France 96 15,324 477 16,186 998 14,432 1117 13,201

Italy 45 19,115 255 18,811 621 16,234 839 15,246

Table 10.15 The number of women developing depression in a 1-year period in Cam-

berwell, South London [15]. sle refers to a ‘Severe Life Event’ (Example 6.2)

Three children Other

under 14 women

sle No sle sle No sle

Depression 9 0 24 4

No depression 12 20 119 231

4. Fit the corresponding quasi-Poisson model. Produce the plot of residuals

against ﬁtted values, and evaluated the model.

5. Fit the corresponding negative binomial glm. Produce the plot of resid-

uals against ﬁtted values, and evaluated the model.

6. Which model seems appropriate, if any?

10.12. In a study of depressed women [15], women were classiﬁed into groups

(Table 10.15; data set: dwomen) based on their depression level (Depression),

whether a severe life event had occurred in the last year (SLE), and if they

had three children under 14 at home (Children). Model these counts using

a Poisson glm, and summarize the data if possible.

10.13. The number of severe and non-severe cyclones in the Australian region

between 1970 and 2005 were recorded (Table 10.16; data set: cyclones),

together with a climatic index called the Ocean Niño Index,oroni.Theoni

is a 3-month running mean of sea surface temperature anomalies; Table 10.16

shows the oni at four times during each year.

1. Plot the number of severe cyclones against the oni, and then plot the

number of non-severe cyclones against the oni. Comment.

2. Fit a Possion glm to model the number of severe cyclones, and another

Poisson glm for the number of non-severe cyclones.

3. Interpret your ﬁnal models.

10.14. A study [13, 18] of the species richness (the number of species) of ants

at 22 sites in New England, usa, examined relationships with habitat (forest

418 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.16 The number of severe and non-severe cyclones in the Australian region,

with four values of the Ocean Niño Index (oni) for each year (Problem 10.13)

Number of cyclones oni

Year Severe Non-severe JFM AMJ JAS OND

1969 3 7 1.00.60.40.8

1970 3 14 0.30.0 −0.8 −0.9

1971 9 7 −1.3 −0.8 −0.8 −1.0

1972 6 6 −0.40.51.32.0

1973 4 15 1.2 −0.6 −1.3 −2.0

1974 3 13 −1.7 −0.9 −0.5 −0.9

Table 10.17 Species richness of ants in New England, usa. Elevation is in metres

(Problem 10.14)

Species richness in: Species richness in:

Elevation Latitude Forest Bog Elevation Latitude Forest Bog

41.97 389 6 5 42.57 335 10 4

42.00 8 16 6 42.58 543 4 2

42.03 152 18 14 42.69 323 5 7

42.05 1 17 7 43.33 158 7 2

42.05 210 9 4 44.06 313 7 3

42.17 78 15 8 44.29 468 4 3

42.19 47 7 2 44.33 362 6 2

42.23 491 12 3 44.50 236 6 3

42.27 121 14 4 44.55 30 8 2

42.31 95 9 8 44.76 353 6 5

42.56 274 10 8 44.95 133 6 5

or bog), elevation (in m) and latitude (Table 10.17; data set: ants). Find a

suitable model for the data. Interpret your ﬁnal model.

10.15. A study [14, 17, 33] compared the number polyps in patients with

familial adenomatous polyposis (Table 10.18; data set: polyps), after treat-

ment with a new drug (sulindac) or a placebo.

1. Plot the data and comment.

2. Find a suitable Poisson glm for modelling the data, and show that

overdispersion exists.

3. Fit a quasi-Poisson model to the data.

4. Fit a negative binomial glm to the data.

5. Decide on a ﬁnal model.

10.16. An experiment [21] compared the density of understorey birds at a

series of sites in two areas either side of a stockproof fence (Table 10.19;

10.8 Summary 419

Table 10.18 The number of polyps in the treatment and placebo group for patients

with famial adenomatous polyposis (Problem 10.15)

Treatment group Placebo group

Number Age Number Age Number Age Number Age

1 22 17 22 7 34 44 19

123251710304622

216332315505034

3 23 2818 6113

3 23 2822 6320

442 4027

Table 10.19 The number of understorey-foraging birds observed in three 20-min sur-

veys of 2 ha quadrats either side of a stockproof fence, before and after grazing (Prob-

lem 10.16)

Ungrazed Grazed

Before After Before After Before After Before After Before After

013752 60 0304

310 750 21 31314

110104000706

19 29 11 4 1 11 4 17 2 8

821 164 70 7 018

30 15 2 4 0 0 1 4

3327

data set: grazing). One side had limited grazing (mainly from native herbi-

vores), and the other was heavily grazed by feral herbivores, mostly horses.

Bird counts were recorded at the sites either side of the fence (the ‘before’

measurements). Then the herbivores were removed, and bird counts recorded

again (the ‘after’ measurements). The measurements are the total number of

understorey-foraging birds observed in three 20-min surveys of 2 ha quadrats.

1. Plot the data, and explain the important features.

2. Fit a Poisson glm with systematic component Birds ~ When * Grazed,

ensuring a diagnostic analysis.

3. Show that overdispersion exists. Demonstrate by computing the mean

and variance of each combination of the explanatory variables.

4. Fit a quasi-Poisson model.

5. Fit a negative binomial glm.

6. Compare all three ﬁtted models to determine a suitable model.

7. Interpret the ﬁnal model.

10.17. An experiment [23, 36] recorded the time to failure of a piece of elec-

tronic equipment while operating in two diﬀerent modes. In any session, the

machine is run in both modes for varying amounts of time (Table 10.20; data

420 10 Models for Counts: Poisson and Negative Binomial GLMs

Table 10.20 Observations on electronic equipment failures. The time spent in each

mode is measured in weeks (Problem 10.17)

Time spent Time spent Number of Time spent Time spent Number of

in Mode 1 in Mode 2 failures in Mode 1 in Mode 2 failures

33.325.3 15 116.353.627

52.214.4 9 131.756.623

64.732.514 85.087.318

137.020.524 91.947.822

125.997.627

Table 10.21 The estimated number of deaths for the ﬁve leading cancer sites in Canada

in 2000, by geographic region and gender (Problem 10.18)

Ontario Newfoundland Quebec

Cancer Male Female Male Female Male Female

Lung 3500 2400 240 95 3500 2000

Colorectal 1250 1050 60 50 1100 1000

Breast 0 2100 0 95 0 1450

Prostate 1600 0 80 0 900 0

Pancreas 540 590 20 25 390 410

Estimated population: 11,874,400 533,800 7,410,500

set: failures). For each operating period, Mode 1 is the time spent operating

in one mode and Mode 2 is the time spent operating in the other mode. The

number of failures in each period is recorded, where each operating period

is measured in weeks. The interest is in ﬁnding a model for the number of

failures given the amount of time the equipment spends in the two modes.

1. Plot the number of failures against the time spent in Mode 1, and then

against the time spent in Mode 2.

2. Show that an identity link function may be appropriate.

3. Fit the Poisson model, to model the number of failures as a function of

the time spent in the two modes. Which mode appears to be the major

source of failures?

4. Is there evidence of under- or overdispersion?

5. Interpret the ﬁnal model.

10.18. A report on Canadian cancer statistics estimated the number of

deaths from various types of cancer in Canada in 2000 [7]. The ﬁve lead-

ing cancer sites are studied here (Table 10.21; data set: ccancer).

1. Plot the cancer rates per thousand of population against each geograph-

ical location, and then against gender. Comment on the relationships.

2. Identify the zeros as systematic or sampling.

3. Find an appropriate model for the data using an appropriate oﬀset. Do

the cancer rates appear to diﬀer across the geographic regions?

4. Interpret the ﬁtted model.

10.8 Summary 421

Table 10.22 Health concerns of teenagers (Problem 10.20)

Health concern

Age Sex; How Nothing

Sex group relationships Menstrual healthy at all

Males 12–15 4 0 42 57

16–17 2 0 7 20

Females 12–15 9 4 19 71

16–17 7 8 10 31

Total 22 12 78 179

Table 10.23 Smoking and survival data for Whickham women (Problem 10.21)

Age Smokers Non-smokers

(at ﬁrst survey) Alive Dead Alive Dead

18–24 53 2 61 1

25–34 121 3 152 5

35–44 95 14 114 7

45–54 103 27 66 12

55–64 64 51 81 40

65–74 7 29 28 101

75+ 0 13 0 64

10.19. In Problem 2.18 (p. 88), data were presented about children building

towers out of building blocks (data set: blocks). One variable measured was

the number of blocks needed to build a tower as high as possible. Find a

model for the number of blocks, including a diagnostic analysis.

10.20. A study [6, 9, 16] asked teenagers about their health concerns, includ-

ing sexual health. The data in Table 10.22 (data set: teenconcerns)arethe

number of teenagers who reported wishing to talk to their doctor about the

indicated topic.

1. How would you classify the zeros? Explain.

2. Fit an appropriate log-linear model to the data.

10.21. A survey originally conducted in 1972–1974 [3, 10] asked women in

Whickham in the north of England about their smoking habits and age, and

recorded their survival (Table 10.23; data set: wwomen). A subsequent survey

20 years later followed up the women to determine how many women from

the original survey had died.

1. Classify the zeros as sampling or structural zeros.

2. Plot the proportion of women alive at each age (treat age as continuous,

using the lower boundary of each class), distinguishing between smokers

and non-smokers. Comment.

422 REFERENCES

3. Compute the overall percentage of smokers and non-smokers alive, and

comment.

4. Compute the percentage of smokers and non-smokers in each age group

who died. Compare to the previous answers. Comment and explain.

5. Fit a suitable log-linear model for the number of women alive. What

evidence is there that the data should not be collapsed over age?

References

[1] Agresti, A.: An Introduction to Categorical Data Analysis, second edn.

Wiley-Interscience, New York (2007)

[2] Andersen, E.B.: Multiplicative Poisson models with unequal cell rates.

Scandinavian Journal of Statistics 4, 153–158 (1977)

[3] Appleton, D.R., French, J.M., Vanderpump, M.P.J.: Ignoring a covariate:

An example of Simpson’s paradox. The American Statistician 50, 340–

341 (1996)

[4] Berkeley, E.C.: Right answers—a short guide for obtaining them. Com-

puters and Automation 18(10) (1969)

[5] Brockmann, H.J.: Satellite male groups in horseshoe crabs, limulus

polyphemus. Ethology 102, 1–21 (1996)

[6] Brunswick, A.F.: Adolescent health, sex, and fertility. American Journal

of Public Health 61(4), 711–729 (1971)

[7] Canadian Cancer Society: Canadian cancer statistics 2000. Published

on the internet: www.cancer.ca/stats2000/tables/tab5e.htm (2000). Ac-

cessed 19 September 2001

[8] Charig, C.R., Webb, D.R., Payne, S.R., Wickham, J.E.A.: Comparison

of treatment of renal calculi by open surgery, percutaneous nephrolitho-

tomy, and extracorporeal shockwave lithotripsy. British Medical Journal

292, 879–882 (1986)

[9] Christensen, R.: Log-Linear Models. Springer Texts in Statistics.

Springer, New York (2013)

[10] Davison, A.C.: Statistical Models. Cambridge University Press, UK

(2003)

[11] Dunn, P.K.: Contingency tables and log-linear models. In: K. Kempf-

Leonard (ed.) Encyclopedia of Social Measurement, pp. 499–506. Else-

vier (2005)

[12] Dunn, P.K., Smyth, G.K.: Randomized quantile residuals. Journal of

Computational and Graphical Statistics 5(3), 236–244 (1996)

[13] Ellison, A.M.: Bayesian inference in ecology. Ecology Letters 7, 509–520

(2004)

[14] Everitt, B.S., Hothorn, T.: A Handbook of Statistical Analyses using,

second edn. Chapman & Hall/CRC, Boca Raton, FL (2010)

REFERENCES 423

[15] Everitt, B.S., Smith, A.M.R.: Interactions in contingency tables: A brief

discussion of alternative deﬁnitions. Psychological Medicine 9, 581–583

(1979)

[16] Fienberg, S.: The Analysis of Cross-Classiﬁed Categorical Data.

Springer, New York (2007)

[17] Giardiello, F.M., Hamilton, S.R., Krush, A.J., Piantadosi, S., Hylind,

L.M., Celano, P., Booker, S.V., Robinson, C.R., Johan, G., Oﬀerhaus,

A.: Treatment of colonic and rectal adenomas with sulindac in famial

adenomatous polyposis. New England Journal of Medicine 328(18),

1313–1316 (1993)

[18] Gotelli, N.J., Ellison, A.M.: Biogeography at a regional scale: Determi-

nants of ant species density in bogs and forests of New England. Ecology

83(6), 1604–1609 (2002)

[19] Hand, D.J., Daly, F., Lunn, A.D., McConway, K.Y., Ostrowski, E.: A

Handbook of Small Data Sets. Chapman and Hall, London (1996)

[20] Health Department of Western Australia: Annual report 1997/1998—

health of Western Australians—mortality and survival. Published on

the internet: www.health.wa.gov.au/Publications/annualreport_9798/.

Accessed 19 September 2001

[21] Howes, A.L., Maron, M., McAlpine, C.A.: Bayesian networks and adap-

tive management of wildlife habitat. Conservation Biology 24(4), 974–

983 (2010)

[22] Hutchinson, M.K., Holtman, M.C.: Analysis of count data using Poisson

regression. Research in Nursing and Health 28, 408–418 (2005)

[23] Jorgensen, D.W.: Multiple regression analysis of a Poisson process. Jour-

nal of the American Statistical Association 56(294), 235–245 (1961)

[24] Julious, S.A., Mullee, M.A.: Confounding and Simpson’s paradox.

British Medical Journal 309(1480), 1480–1481 (1994)

[25] King, G.: Statistical models for political science event counts: Bias in

conventional procedures and evidence for the exponential Poisson re-

gression model. American Journal of Political Science 32(3), 838–863

(1988)

[26] Lindsey, J.K.: Modelling Frequency and Count Data. No. 15 in Oxford

Statistical Science Series. Clarendon Press, Oxford (1995)

[27] Lovett, A.A., Gatrell, A.C.: The geography of spina biﬁda in England

and Wales. Transactions of the Institute of British Geographers (New

Series) 13(3), 288–302 (1988)

[28] Luo, D., Wood, G.R., Jones, G.: Visualising contingency table data. The

Australian Mathematical Society Gazette 31(4), 258–262 (2004)

[29] Maag, J.W., Behrens, J.T.: Epidemiologic data on seriously emotionally

disturbed and learning disabled adolescents: Reporting extreme depres-

sive symptomatology. Behavioral Disorders 15(1) (1989)

[30] Maron, M.: Threshold eﬀect of eucalypt density on an aggressive avian

competitor. Biological Conservation 136, 100–107 (2007)

424 REFERENCES

[31] Norton, J., Lawrence, G., Wood, G.: The Australian public’s perception

of genetically-engineered foods. Australasian Biotechnology pp. 172–181

(1998)

[32] Pettifor, R.A.: Brood-manipulation experiments. I. The number of oﬀ-

spring surviving per nest in blue tits (Parus caeruleus). Journal of An-

imal Ecology 62, 131–144 (1993)

[33] Piantadosi, S.: Clinical Trials: A Methodologic Perspective, second edn.

John Wiley and Sons, New York (2005)

[34] Siegel, R.L., Miller, K.D., Jemal, A.: Cancer statistics, 2015. CA: A

Cancer Journal for Clinicians 65(1), 5–29 (2015)

[35] Smith, P.T., Heitjan, D.F.: Testing and adjusting for departures from

nominal dispersion in generalized linear models. Journal of the Royal

Statistical Society, Series C 42(1), 31–41 (1993)

[36] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

[37] Venables, W.N., Ripley, B.D.: Modern Applied Statistics with S, fourth

edn. Springer-Verlag, New York (2002). URL http://www.stats.ox.ac.

uk/pub/MASS4

[38] Whittemore, A.S., Gong, G.: Poisson regression with misclassiﬁed

counts: Applications to cervical cancer mortality rates. Journal of the

Royal Statistical Society, Series C 40(1), 81–93 (1991)

Chapter 11

Positive Continuous Data: Gamma

and Inverse Gaussian GLMs

It has been said that data collection is like garbage

col lection: before you collect it you should have in mind

whatyouaregoingtodowithit.

Fox, Garbuny and Hooke [6, p. 51]

11.1 Introduction and Overview

This chapter considers models for positive continuous data. Variables that

take positive and continuous values often measure the amount of some physi-

cal quantity that is always present. The two most common glms for this type

of data are based on the gamma and inverse Gaussian distributions. Judicious

choice of link function and transformations of the covariates ensure that a va-

riety of relationships between the response and explanatory variables can be

modelled. Modelling positive continuous data is introduced in Sect. 11.2, then

the two most common edms for modelling positive continuous data are dis-

cussed: gamma distributions (Sect. 11.3) and inverse Gaussian distributions

(Sect. 11.4). The use of link functions is then addressed (Sect. 11.5). Finally,

estimation of φ is considered in Sect. 11.6.

11.2 Modelling Positive Continuous Data

Many applications have response variables which are continuous and posi-

tive. Such variables usually have distributions that are right skew, because

the boundary at zero limits the left tail of the distribution. If the values

of such a variable vary by orders of magnitude, then such skewness is in-

evitable. Another consequence of the boundary at zero is that the variance of

the response must generally approach zero as the expected value approaches

zero, provided the structure of the distribution remains otherwise the same

(Sect. 4.2). Positive continuous data therefore usually shows an increasing

mean–variance relationship.

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_11

425

426 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

Table 11.1 Measurements from small-leaved lime trees in Russia, grouped by the origin

of the tree. Foliage refers to the foliage biomass, and dbh refers to the ‘diameter at breast

height’ (Example 11.1)

Natural Coppice Planted

Foliage dbh Age Foliage dbh Age Foliage dbh Age

(in kg) (in cm) (in years) (in kg) (in cm) (in years) (in kg) (in cm) (in years)

0.10 4.00 38 0.27 7.20 24 0.92 16.40 38

0.20 6.00 38 0.03 3.10 11 3.69 18.40 38

0.40 8.00 46 0.04 3.30 12 0.82 12.80 37

0.60 9.60 44 0.03 3.10 11 1.09 14.10 42

0.60 11.30 60 0.01 3.30 12 0.08 6.40 35

0.80 13.70 56 0.07 3.30 12 0.59 12.00 32

Apart from V (μ)=μ, which we have already seen corresponds to count

data, the simplest increasing variance function functions are V (μ)=μ

and

V (μ)=μ

, which correspond to the gamma and inverse Gaussian distribu-

tions respectively. For these reasons, glms based on the gamma and inverse

Gaussian distributions are useful for modelling positive continuous data. The

gamma distribution corresponds to ratio data with constant coeﬃcient of

variation. A gamma glm is speciﬁed in r using family=Gamma(),andan

inverse Gaussian glm using family=inverse.gaussian().

Example 11.1. A series of studies [22] sampled the forest biomass in Eura-

sia [21]. Part of that data, for small-leaved lime trees (Tilia cordata), is shown

in Table 11.1 (data set: lime).

A model for the foliage biomass y is sought. The foliage mostly grows

on the outer canopy, which could be crudely approximated as a spherical

shape, so one possible model is that the mean foliage biomass μ may be

related to the surface area of the approximately-spherical canopy. In turn,

the canopy diameter may be proportional to the diameter of the tree trunk

(or dbh), d. This suggests a model where μ is proportional to the surface

area 4π(d/2)

= πd

; taking logs, log y ∝ log π + 2 log d. In addition, the

tree diameter may be related to the age of the tree. However, since diameter

measures some physical quantity and is easier to measure precisely, expect

the relationship between foliage biomass and dbh to be stronger than the

relationship between foliage biomass and age.

> library(GLMsData); data(lime); str(lime)

'data.frame': 385 obs. of 4 variables:

$ Foliage: num 0.1 0.2 0.4 0.6 0.6 0.8 1 1.4 1.7 3.5 ...

$ DBH : num 4 6 8 9.6 11.3 13.7 15.4 17.8 18 22 ...

$ Age : int 38 38 46 44 60 56 72 74 68 79 ...

$ Origin : Factor w/ 3 levels "Coppice","Natural",..: 2222222

222...

11.3 The Gamma Distribution 427

> # Plot Foliage against DBH

> plot(Foliage ~ DBH, type="n", las=1,

xlab="DBH (in cm)", ylab="Foliage biomass (in kg)",

ylim = c(0, 15), xlim=c(0, 40), data=lime)

> points(Foliage ~ DBH, data=subset(lime, Origin=="Coppice"),

pch=1)

> points(Foliage ~ DBH, data=subset(lime, Origin=="Natural"),

pch=2)

> points(Foliage ~ DBH, data=subset(lime, Origin=="Planted"),

pch=3)

> legend("topleft", pch=c(1, 2, 3),

legend=c("Coppice", "Natural","Planted"))

> # Plot Foliage against DBH, on log scale

> plot( log(Foliage) ~ log(DBH), type="n", las=1,

xlab="log of DBH (in cm)", ylab="log of Foliage biomass (in kg)",

ylim = c(-5, 3), xlim=c(0, 4), data=lime)

> points( log(Foliage) ~ log(DBH), data=subset(lime, Origin=="Coppice"),

pch=1)

> points( log(Foliage) ~ log(DBH), data=subset(lime, Origin=="Natural"),

pch=2)

> points( log(Foliage) ~ log(DBH), data=subset(lime, Origin=="Planted"),

pch=3)

> # Plot Foliage against Age

> plot(Foliage ~ Age, type="n", las=1,

xlab="Age (in years)", ylab="Foliage biomass (in kg)",

ylim = c(0, 15), xlim=c(0, 150), data=lime)

> points(Foliage ~ Age, data=subset(lime, Origin=="Coppice"), pch=1)

> points(Foliage ~ Age, data=subset(lime, Origin=="Natural"), pch=2)

> points(Foliage ~ Age, data=subset(lime, Origin=="Planted"), pch=3)

> # Plot Foliage against Origin

> plot( Foliage ~ Origin, data=lime, ylim=c(0, 15),

las=1, ylab="Foliage biomass (in kg)")

Clearly, the response is always positive. From Fig. 11.1, the variance in

foliage biomass increases as the mean increases, and a relationship exists

between foliage biomass and dbh, and between foliage biomass and age. The

eﬀect of origin is harder to see. 

11.3 The Gamma Distribution

The probability function for a gamma distribution is commonly written as

P(y; α, β)=

α−1

exp(−y/β)

Γ (α)β

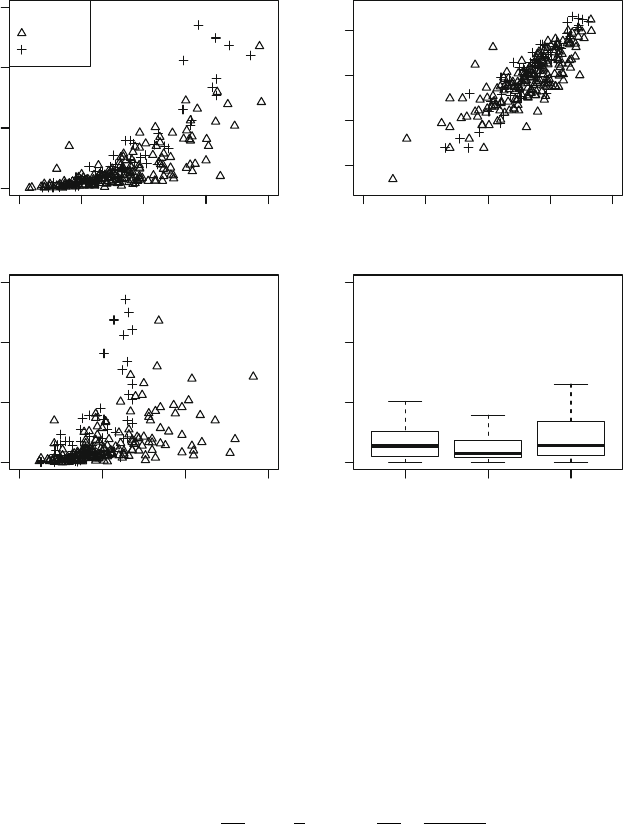
428 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

010203040

DBH (in cm)

Foliage biomass (in kg)

Coppice

Natural

Planted

01234

−4

−2

log of DBH (in cm)

log of Foliage biomass (in kg)

0 50 100 150

Age (in years)

Foliage biomass (in kg)

Coppice Natural Planted

Origin

Foliage biomass (in kg)

Fig. 11.1 The small-leaved lime data. Foliage biomass against dbh (diameter at breast

height; top left panel); log of foliage biomass against the log of dbh (diameter at breast

height; top right panel); foliage biomass against age (bottom left panel) foliage biomass

against origin (bottom right panel) (Example 11.1)

for y>0, α>0 (the shape parameter) and β>0 (the scale parameter),

where E[y]=αβ and var[y]=αβ

. Note that Γ () is the gamma function

(where, for example, if n is a non-negative integer then Γ (n)=(n − 1)!).

Writing in terms of μ and φ, the probability function becomes

P(y; μ, φ)=



φμ



1/φ

exp



−

φμ



Γ (1/φ)

for y>0, and μ>0andφ>0, where α =1/φ and β = μφ. Plots of some

example gamma probability functions are shown in Fig. 11.2. The variance

function for the gamma distribution is V (μ)=μ

.Thecoeﬃcient of variation

is deﬁned as the ratio of the variance to the mean squared, and is a mea-

sure of the relative variation in the data. Therefore, the gamma distribution

has a constant coeﬃcient of variation, and consequently gamma glmsare

useful in situations where the coeﬃcient of variation is (approximately) con-

stant. Useful information about the gamma distribution appears in Table 5.1

(p. 221).

11.3 The Gamma Distribution 429

Gamma density:

Mean: 0.75

Density

012345

Gamma density:

Mean: 1.0

Density

Variance: 1

Variance: 0.5

012345

Gamma density:

Mean: 2.0

Density

012345

Fig. 11.2 Some example gamma probability functions (Sect. 11.3)

−0.5 0.0 0.5 1.0 1.5

−1

log(group means)

log(group variance)

Fig. 11.3 The small-leaved limed data: the logarithm of group variances plotted against

the logarithm of the group means (Example 11.2)

Example 11.2. For the small-leaved lime data (Example 11.1; data set: lime),

the data can be split into smaller groups, and the mean and variance of each

group calculated. Then, Fig. 11.3 shows that the variance increases as the

mean increases:

> # Define age *groups*

> lime$AgeGrp <- cut(lime$Age, breaks=4 )

> # Now compute means and variances of each origin/age group:

> vr <- with( lime, tapply(Foliage, list(AgeGrp, Origin), "var" ) )

> mn <- with( lime, tapply(Foliage, list(AgeGrp, Origin), "mean" ) )

> # Plot

> plot( log(vr) ~ log(mn), las=1, pch=19,

xlab="log(group means)", ylab="log(group variance)")

430 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

> mf.lm <- lm( c(log(vr)) ~ c(log(mn)) )

> coef( mf.lm )

(Intercept) c(log(mn))

-0.165002 1.706453

> abline( coef( mf.lm ), lwd=2)

The slope of the line is a little less than 2, so approximately

log(group variance) ∝ 2 × log(group mean).

Re-arranging shows the group variance is approximately proportional to

square of the group mean. In other words, V (μ) ≈ μ

which corresponds

to a gamma distribution (Sect. 5.3.6). 

For the gamma distribution, φ is almost always unknown and therefore

must be estimated (Sect. 11.6.1), so likelihood ratio tests are based on F -tests

(Sect. 7.6.4). Two common situations exist where φ is known. In situations

where y follows a normal distribution, the sample variances can be modelled

using a chi-square distribution, which is a gamma distribution with φ =

2. Secondly, the exponential distribution (4.37), which has a history of its

own apart from its connection with the gamma distribution, is a gamma

distribution with φ = 1 (see Problem 11.17).

The unit deviance for the gamma distribution is

d(y, μ)=2



−log

y −μ



. (11.1)

The residual deviance D(y, ˆμ)=



i=1

d(y

, ˆμ

) ∼ χ

n−p



approximately, by

the saddlepoint approximation, for a model with p



parameters in the linear

predictor. The saddlepoint approximation is adequate if φ ≤ 1/3 (Sect. 7.5,

p. 276).

The canonical link function for the gamma distribution is the inverse (or

reciprocal) link function η =1/μ. In practice, the logarithmic link function is

often used because it avoids the need for constraints on the linear predictor

in view of μ>0. The log-link often also leads to a useful interpretation

where the impact of the explanatory variables is multiplicative (as discussed

in the context of Poisson glms; see Sect. 10.2). Other link functions are used

sometimes to produce desirable features (Sect. 11.5).

The gamma distribution can be used to describe the time between occur-

rences that follow a Poisson distribution. More formally, suppose an event

occurs over a time interval of length T at the Poisson rate of λ events per

unit time. Assuming the probability of more than one event in a very small

time interval is small, then the number of events in the interval from time 0

to time T can be modelled using a Poisson distribution. Then the length

of time y required for r events to occur follows a gamma distribution, with

mean r/λ and variance r/λ

. In this interpretation, r is an integer, which

11.4 The Inverse Gaussian Distribution 431

0 50 100 150

The cumulative number of events

over time

Time

Cumulative number of events

y = 45

y = 54

y = 18

0 20 40 60 80 100 120

0.000

0.005

0.010

0.015

0.020

0.025

0.030

Distribution of time y required to reach

r = 10 across 10000 simulations

Time required between

occurrence of 10 events

Density

Empirical

Gamma

Fig. 11.4 The gamma distribution describes the time between Poisson events. Left

panel: the occurrence of the Poisson events showing the time y between the occurrence

of r = 10 Poisson events for the ﬁrst three occurrences only. Right panel: the distribution

of the time y between events has a gamma distribution (Example 11.3)

is not true in general for the gamma distribution. When r is an integer, the

gamma distribution is also called the Erlang distribution.

Example 11.3. Suppose events occur over a time interval of T = 1 at the rate

of λ =0.2 per unit time. The length of time y for r = 10 events to occurs

is shown in Fig. 11.4 (left panel) for the ﬁrst three sets of r =10events.

The distribution of these times has an approximate gamma distribution with

mean r/λ =10/0.2 = 50 and variance r/λ

=10/0.2

= 250 (Fig. 11.4, right

panel).



11.4 The Inverse Gaussian Distribution

The inverse Gaussian distribution may sometimes be suitable for modelling

positive continuous data. The inverse Gaussian has the probability function

P(y; μ, φ)=(2πy

φ)

−1/2

exp



−

2φ

(y −μ)

yμ



(11.2)

where y>0, for μ>0 and the dispersion parameter φ>0. The variance

function is V (μ)=μ

. The inverse Gaussian distribution is used when the

responses are even more skewed than suggested by the gamma distribution.

Plots of some example inverse Gaussian densities are shown in Fig. 11.5.

The canonical link function for the inverse Gaussian distribution is

η = μ

−2

, though other link functions are almost always used in practice

432 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

Inverse Gaussian density:

Mean: 0.75

Density

012345

Inverse Gaussian density:

Mean: 1.0

Density

Variance: 1

Variance: 0.5

012345

Inverse Gaussian density:

Mean: 2.0

Density

012345

Fig. 11.5 Some example inverse Gaussian probability functions (Sect. 11.4)

(Sect. 11.5), often to ensure μ>0 and for interpretation purposes. The unit

deviance for the inverse Gaussian distribution is

d(y, μ)=

(y −μ)

yμ

when the residual deviance is D(y, ˆμ)=



i=1

d(y

, ˆμ

), where the w

are

the prior weights. The unit deviance for the inverse Gaussian distribution is

distributed exactly as χ

(Sect. 5.4.3), since the saddlepoint approximation

is exact for the inverse Gaussian distribution (Problem 11.4). This means

D(y, ˆμ) ∼ χ

n−p



exactly (apart from sampling error in estimating μ

and φ)

for a model with p



parameters in the linear predictor. Useful information

about the inverse Gaussian distribution appears in Table 5.1 (p. 221). For

the inverse Gaussian distribution, φ is almost always unknown and estimated

(Sect. 11.6.2), so likelihood ratio tests are based on F -tests (Sect. 7.6.4).

The inverse Gaussian distribution has an interesting interpretation, con-

nected to Brownian motion. Brownian motion is the name given to the ran-

dom movement of particles over time. For a particle moving with Brown-

ian motion with positive drift (the tendency to move from the current loca-

tion), the inverse Gaussian distribution describes the distribution of the time

taken for the particle to reach some point that is a ﬁxed positive distance

δ away. The normal distribution, also known as the Gaussian distribution,

describes the distribution of distance from the origin at ﬁxed time. The in-

verse Gaussian distribution gets its name from this relationship to the normal

distribution.

To demonstrate these connections between the normal and inverse Gaus-

sian distribution in r, consider a particle moving with Brownian motion with

drift 0.5. We can measure both the time taken to exceed a ﬁxed value δ =5

from the origin, and the distance of the particle from the origin after T = 20.

11.5 Link Functions 433

0 10203040

One realization of the

location of a particle

Time

Distance from origin

Threshold: 5

y = 7

010 30 50

0.00

0.02

0.04

0.06

0.08

0.10

Time taken to reach delta

across 1000 simulations

Time taken to reach threshold

Density

Empirical

Inv. Gaussian

−2 0 2

−5

Q−Q plot of distribution

of location from origin

Theoretical Quantiles

Sample Quantiles

Fig. 11.6 The connection between Brownian motion, the inverse Gaussian distribution

and the normal distribution. Left panel: the location of the particle x

at time t;centre

panel: the distribution of the time taken for the particle to exceed δ = 5 follows an

inverse Gaussian distribution; right panel: the distance of the particle from the origin

after T = 20 follows a normal distribution (Sect. 11.4)

The distribution of the time taken closely resembles the expected inverse

Gaussian distribution (Fig. 11.6, centre panel), and the distance of the par-

ticle from the origin closely follows a normal distribution (Fig. 11.6, right

panel).

11.5 Link Functions

The logarithmic link function is the link function most commonly used for

gamma and inverse Gaussian glms, to ensure μ>0 and for interpretation

purposes (Sect. 10.2). For the gamma and inverse Gaussian distributions, r

permits the link functions "log", "identity" and "inverse" (the default

for the gamma distribution). The link function link="1/mu^2" is also per-

mitted for the inverse Gaussian distribution, and is the default (canonical)

link function.

Example 11.4. For the small-leaved lime data in Example 11.1 (data set:

lime), no turning points or asymptotes are evident. Consider using a gamma

distribution with a variety of link functions, starting with the commonly-used

logarithmic link function, and using the ideas developed in Example 11.1 for

the model:

> lime.log <- glm( Foliage ~ Origin * log(DBH), family=Gamma(link="log"),

data=lime)

434 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

We next try the inverse link function:

> lime.inv <- update(lime.log, family=Gamma(link="inverse") )

Error: no valid set of coefficients has been found: please supply starting

values

In addition: Warning message:

In log(ifelse(y == 0, 1, y/mu)) : NaNs produced

Using the inverse link function produces error messages: r cannot ﬁnd

suitable starting points (which may indicate a poor model). This is because

the inverse link function does not restrict μ to be positive. To help r ﬁnd a

starting point for ﬁtting the model, starting points may be supplied to glm()

on the scale of the data (using the input mustart) or on the scale of the

linear predictor (using the input etastart). For example, we can provide the

ﬁtted values from lime.log as a starting point:

> lime.inv <- update(lime.log, family=Gamma(link="inverse"),

mustart=fitted(lime.log) )

Error: no valid set of coefficients has been found: please supply starting

values

In addition: Warning message:

In log(ifelse(y == 0, 1, y/mu)) : NaNs produced

The model still can not be ﬁtted, so we do not consider this model further.

Finally, we try the identity link function:

> lime.id <- update(lime.log, family=Gamma(link="identity"),

mustart = fitted(lime.log) )

Error: no valid set of coefficients has been found: please supply starting

values

In addition: Warning message:

In log(ifelse(y == 0, 1, y/mu)) : NaNs produced

Warning messages are displayed when ﬁtting the model with the identity link

function: the algorithm did not converge. Again, we could supply starting

values to the algorithm to see if this helps:

> lime.id <- update(lime.log, family=Gamma(link="identity"),

mustart=fitted(lime.log) )

Error: no valid set of coefficients has been found: please supply starting

values

In addition: Warning message:

In log(ifelse(y == 0, 1, y/mu)) : NaNs produced

The glm with the identity link function still does not converge, so we do not

consider this model any further. The inverse-link and identity-link models

are not very sensible in any case, given Fig. 11.1.

For the log-link model, standard residual plots (using quantile residuals [4])

show that the model seems appropriate (Fig. 11.7):

11.5 Link Functions 435

−3 −2 −1 0 1 2

−2

−1

Log link

Log of fitted values

Standardized residuals

−3 −2 −1 0 1 2

−4

−2

Linear predictor, eta

Working resid

−3 −2 −1 0 1 2 3

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

0 100 200 300 400

0.00

0.05

0.10

0.15

0.20

Index

Cook's distance

Fig. 11.7 Plots of the standardized residuals against the ﬁtted values for two gamma

glms ﬁtted to the small-leaved lime data. Left panels: using a logarithmic link function;

right panels: using an inverse link function; top panels: standardized residuals plotted

against log ˆμ; centre panels: the working residuals e plotted against ˆη; bottom panels:

Q–Q plots of the quantile residuals (Example 11.4)

> ## STDIZD RESIDUALS vs FITTED VALUES on constant-info scale

> plot(rstandard(lime.log) ~ log(fitted(lime.log)), main="Log link", las=1,

xlab="Log of fitted values", ylab="Standardized residuals")

> ## CHECK LINEAR PREDICTOR

> eta.log <- lime.log$linear.predictor

> plot(resid(lime.log, type="working") + eta.log ~ eta.log, las=1,

ylab="Working resid", xlab="Linear predictor, eta")

> ## QQ PLOT OF RESIDUALS

> qqnorm( qr1 <- qresid(lime.log), las=1 ); qqline( qr1 )

> ## COOK'S DISTANCE

> plot( cooks.distance(lime.log), ylab="Cook's distance", las=1, type="h")

Some observations produce large residuals, and some observations appear to

give a value of Cook’s distance larger than the others though none are deemed

inﬂuential:

> colSums(influence.measures(lime.log)$is.inf)

dfb.1_ dfb.OrgN dfb.OrgP dfb.l(DB dfb.ON:( dfb.OP:( dffit cov.r

000000729

cook.d hat

018



436 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

0.0 1.0 2.0 3.0

log(μ) = 1 + x

0.0 1.0 2.0 3.0

0.5

1.0

1.5

2.0

2.5

log(μ) = 1 − x

0.0 1.0 2.0 3.0

100

log(μ) = 1 + x + 1 x

0.0 1.0 2.0 3.0

0.0

0.1

0.2

0.3

log(μ) = 1 − x − 1 x

0.0 1.0 2.0 3.0

0.0

0.5

1.0

1.5

2.0

log(μ) = 1 + 0.02x − 1 x

0.0 1.0 2.0 3.0

log(μ) = 1 − 0.02x + 1 x

Fig. 11.8 Various logarithmic link function relationships, based on [15, Figure 8.4]

(Sect. 11.5)

While the logarithmic link function is commonly used, judicious use of

the logarithmic and inverse link functions with transformations of covariates

accommodates a wide variety of relationships between the variables, including

data displaying asymptotes (Figs. 11.8 and 11.9). Polynomial relationships

cannot bound the value of μ, so non-polynomial linear predictors make more

physical sense in applications where asymptotes are present. Yield–density

experiments (Sect. 11.7.2) are one example where these relationships are used.

11.6 Estimating the Dispersion Parameter

11.6.1 Estimating φ for the Gamma Distribution

For the gamma distribution, the maximum likelihood estimate (mle)ofthe

dispersion parameter φ cannot be found in closed form. Deﬁning the digamma

function as ψ(x)=Γ (x)



/Γ (x), the mle of φ is the solution to

D(y, ˆμ)=−2



i=1

log φ − w

log w

+ w

ψ(w

/φ) (11.3)

11.6 Estimating the Dispersion Parameter 437

1234

0.2

0.3

0.4

0.5

0.6

0.7

0.8

1 μ=1 + x

0246810

0.2

0.4

0.6

0.8

1 μ=1 + 1 x

0246810

0.1

0.2

0.3

0.4

0.5

1 μ=−2 + x + 4 x

0246810

0.0

0.2

0.4

0.6

0.8

1 μ=1 + x + x

Fig. 11.9 Various inverse link function relationships, based on [15, Figure 8.4])

(Sect. 11.5)

where D(y, ˆμ) is the residual deviance and n the sample size (Problem 11.1).

Solving (11.3)forφ requires iterative numerical methods. This is one reason

why the Pearson and deviance estimates are generally used.

Because the deviance is sensitive to very small values of y

for gamma

edms (Sect. 6.8.6), the Pearson estimator

φ =

n − p





i=1

− ˆμ

)

ˆμ

is recommended over the mean deviance estimator

φ =

D(y, ˆμ)

n − p



for the gamma distribution when the accuracy of small values is in doubt,

for example when observations have been rounded to a limited number of

digits [15].

Example 11.5. Consider the gamma glm lime.log ﬁtted in Example 11.4 to

the small-leaved lime data (data set: lime). Two estimates of φ are:

> phi.md <- deviance(lime.log)/df.residual(lime.log) # Mn dev estimate

> phi.pearson <- summary( lime.log )$dispersion # Pearson estimate

> c( "Mean Deviance"=phi.md, "Pearson"=phi.pearson)

438 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

Mean Deviance Pearson

0.4028747 0.5443774

Using numerical methods (Problem 11.1), the mle is 0.3736. 

Example 11.6. Using the model lime.log for the small-leaved lime data in

Example 11.1 (data set: lime), the analysis of deviance table is:

> round(anova(lime.log, test="F"), 3)

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 384 508.48

Origin 2 19.89 382 488.59 18.272 <2e-16 ***

log(DBH) 1 328.01 381 160.58 602.535 <2e-16 ***

Origin:log(DBH) 2 7.89 379 152.69 7.247 0.001 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

By default, r uses the Pearson estimate of φ to produce this output. An F -

test is requested since φ is estimated. Other estimates of φ can be used also:

> round(anova(lime.log,test="F", dispersion=phi.md), 3)

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 384 508.48

Origin 2 19.89 382 488.59 24.690 < 2.2e-16 ***

log(DBH) 1 328.01 381 160.58 814.165 < 2.2e-16 ***

Origin:log(DBH) 2 7.89 379 152.69 9.793 < 2.2e-16 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The conclusions are very similar for either estimate of φ in this example.

Retaining all model terms, the parameter estimates are:

> printCoefmat(coef(summary(lime.log)), 3)

Estimate Std. Error t value Pr(>|t|)

(Intercept) -4.629 0.276 -16.79 <2e-16 ***

OriginNatural 0.325 0.388 0.84 0.4037

OriginPlanted -1.528 0.573 -2.67 0.0079 **

log(DBH) 1.843 0.102 18.15 <2e-16 ***

OriginNatural:log(DBH) -0.204 0.143 -1.42 0.1554

OriginPlanted:log(DBH) 0.577 0.209 2.76 0.0061 **

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Notice that the reference level for Origin is Coppice, and that there is little

evidence of a diﬀerence between the natural and coppice trees. From the

model proposed in Example 11.1, the coeﬃcient for dbh was expected to

be approximately 2; the estimate above is close to this value, and a formal

hypothesis tests could be conducted. 

11.6 Estimating the Dispersion Parameter 439

11.6.2 Estimating φ for the Inverse Gaussian

Distribution

For the inverse Gaussian distribution, the mle of the dispersion parameter

is exactly (Problem 11.3)

φ =

D(y, ˆμ)

As usual, the mle of φ is biased. However the mean deviance estimator

φ =

D(y, ˆμ)

n − p



is essentially the same as the modiﬁed proﬁle likelihood estimator, and is

very nearly unbiased. The mean deviance estimator has theoretically good

properties, and it recommended when good quality data is available. The

Pearson estimator is

φ =

n − p





i=1

− ˆμ

)

ˆμ

As with the gamma distribution, the deviance is sensitive to rounding errors

in very small values of y

(Sect. 6.8.6), so the Pearson estimator may be

better than mean deviance estimator when small values of y are recorded to

less than two signiﬁcant ﬁgures. As always, the Pearson estimator is used in

r by default.

Example 11.7. For the small-leaved lime data (Example 11.1; data set: lime),

an inverse Gaussian glm could also be considered.

> lime.iG <- glm( Foliage ~ Origin * log(DBH),

family=inverse.gaussian(link="log"), data=lime)

The estimates of φ are:

> phi.iG.mle <- deviance(lime.iG)/length(lime$Foliage) # ML estimate

> phi.iG.md <- deviance(lime.iG)/df.residual(lime.iG) # Mean dev

> phi.iG.pearson <- summary( lime.iG )$dispersion # Pearson

> c( "MLE"=phi.iG.mle, "Mean dev."=phi.iG.md, "Pearson"=phi.iG.pearson)

MLE Mean dev. Pearson

1.056659 1.073387 1.255992

The aic suggests the gamma glm is preferred over the inverse Gaussian glm:

> c( "Gamma:"=AIC(lime.log), "inv. Gauss.:"=AIC(lime.iG) )

Gamma: inv. Gauss.:

750.3267 1089.5297



440 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

11.7 Case Studies

11.7.1 Case Study 1

In a study of sheets of building materials [8, 12], the permeability of three

sheets was measured on three diﬀerent machines over nine days, for a total of

81 sheets, all of equal thickness. Each measurement is an average permeabil-

ity of eight random pieces cut from each of the 81 sheets (Table 11.2; data

set: perm). The inverse Gaussian model may be appropriate: particles move

at random according to Brownian motion through the building material as-

suming uniform material, drifting across the sheet (Sect. 11.4). Plots of the

data (Fig. 11.10) show that the variance increases with the mean, and shows

one large observation that is a potential outlier:

> data(perm); perm$Day <- factor(perm$Day)

> boxplot( Perm ~ Day, data=perm, las=1, ylim=c(0, 200),

xlab="Day", ylab="Permeability (in s)")

> boxplot( Perm ~ Mach, data=perm, las=1, ylim=c(0, 200),

xlab="Machine", ylab="Permeability (in s)")

Because the inverse Gaussian distribution has a sensible interpretation

for these data, we adopt the inverse Gaussian model. We also select the

logarithmic link function, when the parameters are interpreted as having a

multiplicative eﬀect on the response:

> perm.log <- glm( Perm ~ Mach * Day, data=perm,

family=inverse.gaussian(link="log") )

> round( anova( perm.log, test="F"), 3)

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 80 0.617

Mach 2 0.140 78 0.477 14.133 <2e-16 ***

Day 8 0.069 70 0.408 1.747 0.108

Table 11.2 The average permeability (in seconds) of eight sheets of building materials

(Sect. 11.7.1)

Machine Machine Machine

Day A B C Day A B C Day A B C

1 25.35 20.23 85.51 4 77.09 47.10 52.60 7 82.79 16.94 21.28

22.18 42.26 47.21 30.55 23.55 33.73 85.31 32.21 63.39

41.50 25.70 25.06 24.66 13.00 23.50 134.59 27.29 24.27

2 27.99 17.42 26.67 5 59.16 16.87 20.89 8 69.98 38.28 48.87

37.07 15.31 58.61 53.46 24.95 30.83 61.66 42.36 177.01

66.07 32.81 72.28 35.08 33.96 21.68 110.15 19.14 62.37

3 82.04 32.06 24.10 6 46.24 25.35 42.95 9 34.67 43.25 50.47

29.99 37.58 48.98 34.59 28.31 40.93 26.79 11.67 23.44

78.34 44.57 22.96 47.86 42.36 22.86 50.58 24.21 69.02

11.7 Case Studies 441

123456789

100

150

200

Day

Permeability (in s)

ABC

100

150

200

Machine

Permeability (in s)

Fig. 11.10 The permeability data. Permeability plotted against the day (left panel),

and permeability plotted against the machine (right panel) (Sect. 11.7.1)

Mach:Day 16 0.110 54 0.298 1.382 0.186

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

Recall the deviance has an exact distribution for the inverse Gaussian dis-

tribution, so these results do not rely on small-dispersion or large-sample

asymptotics. The interaction term is not necessary in the model. The eﬀect

of Day is marginal, and so we omit Day from the model also.

> perm.log <- update( perm.log, Perm ~ Mach)

In this case, the model is simply modelling the means of these three machines:

> tapply( perm$Perm, perm$Mach, "mean") # Means from the data

ABC

54.65704 28.84963 45.98037

> tapply( fitted(perm.log), perm$Mach, "mean") # Fitted means

ABC

54.65704 28.84963 45.98037

The ﬁnal model is:

> printCoefmat(coef(summary(perm.log)))

Estimate Std. Error t value Pr(>|t|)

(Intercept) 4.00108 0.11694 34.2137 < 2.2e-16 ***

MachB -0.63898 0.14455 -4.4205 3.144e-05 ***

MachC -0.17286 0.15868 -1.0894 0.2794

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The model suggests the permeability measurements on Machine B are, on

average, exp(−0.6390) = 0.5278 times those for Machine A (the reference

442 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

level). Likewise, the permeability measurements on Machine C are, on aver-

age, exp(−0.1729) = 0.8413 times those for Machine A. The output suggests

Machine C is very similar to Machine A, but Machine B is diﬀerent.

We can now examine the ﬁtted model to determine if the large observation

identiﬁed in Fig. 11.10 is an outlier, and if it is inﬂuential:

> range( rstudent(m1) )

[1] -2.065777 1.316577

> colSums(influence.measures(m1)$is.inf)

dfb.1_ dfb.x dffit cov.r cook.d hat

000200

No residuals appear too large. No observations are inﬂuential according to

Cook’s distance or dffits.

11.7.2 Case Study 2

Consider results from an experiment [16] to test the yields of three new

onion hybrids (Table 11.3; Fig. 11.11, left panel; data set: yieldden). This is

an example of a yield–density experiment [2, §17.3], [15, §8.3.3].

Yield per plant,sayz, and planting density, say x, usually exhibit an

inverse functional relationship such that

E[z]=

+ β

x + β

. (11.4)

Yield per unit area, y = xz, is usually of interest but is harder to measure

directly than yield per plant z. However,

μ =E[y]=xE[z]=

+ β

x + β

. (11.5)

Table 11.3 Plant yield density for an experiment with onion hybrids. The yields are

the mean yields per plant (in g); the density is in plants per square foot. The yields are

means over three plants, averaged on the log-scale (Example 11.7.2)

Variety 1 Variety 2 Variety 3

Yield Density Yield Density Yield Density

105.6 3.07 131.6 2.14 116.8 2.48

89.4 3.31 109.1 2.65 91.6 3.53

71.0 5.97 93.7 3.80 72.7 4.45

60.3 6.99 72.2 5.24 52.8 6.23

47.6 8.67 53.1 7.83 48.8 8.23

37.7 13.39 49.7 8.72 39.1 9.59

30.3 17.86 37.8 10.11 30.3 16.87

24.2 21.57 33.3 16.08 24.2 18.69

20.8 28.77 24.5 21.22 20.0 25.74

18.5 31.08 18.3 25.71 16.3 30.33

11.7 Case Studies 443

0 5 10 15 20 25 30

100

120

Yield per plant vs density

for onion growing experiment

Planting density (plants/sq. feet), x

Mean yield/plant (g/plant), z

Var. 1

Var. 2

Var. 3

0 5 10 15 20 25 30

300

350

400

450

500

550

600

Yield per unit area vs density

for onion growing experiment

Planting density (plants/sq. feet), x

Mean yield/area (g/sq. feet), y

Var. 1

Var. 2

Var. 3

Fig. 11.11 The yield–density onion data. Yield per plant z against planting density x

(left panel); yield per unit area y against planting density x (right panel) (Sect. 11.7.2)

Then inverting,

= β

+ β

x + β





= η. (11.6)

The bottom left panel of Fig. 11.9 (p. 437) also shows this relationship be-

tween the two variables is appropriate: E[z] → 0asx →∞(that is, as the

planting density becomes very large the mean yield per plant diminishes) and

μ → 0asx → 0 (that is, as the planting density becomes almost zero the

mean yield per unit area diminishes). The plot of the mean yield per unit

area (Fig. 11.11, right panel) shows that as density increases, the yield per

unit area is more variable also. For this reason, we try using a gamma glm.

Hence, we model yield per unit area y using an inverse link function, with a

gamma edm:

> data(yieldden); yieldden$Var <- factor(yieldden$Var)

> yieldden$YD <- with(yieldden, Yield * Dens )

We adopt the theory-based model (11.6), adding interactions between the

terms involving Dens and Var to the model (note the use of the I() function).

> yd.glm.int <- glm( YD ~ (Dens + I(1/Dens)) * Var,

family=Gamma(link=inverse), data=yieldden )

> round( anova( yd.glm.int, test="F"), 2)

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 29 1.45

Dens 1 1.00 28 0.45 191.67 <2e-16 ***

I(1/Dens) 1 0.27 27 0.18 51.28 <2e-16 ***

Var 2 0.06 25 0.12 5.48 0.01 **

Dens:Var 2 0.01 23 0.12 0.57 0.57

I(1/Dens):Var 2 0.01 21 0.11 0.53 0.59

444 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

None of the interaction terms are signiﬁcant. Reﬁt the model with no inter-

actions:

> yd.glm <- update( yd.glm.int, . ~ Dens + I(1/Dens) + Var )

> round( anova(yd.glm, test="F"), 2)

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 29 1.45

Dens 1 1.00 28 0.45 209.56 <2e-16 ***

I(1/Dens) 1 0.27 27 0.18 56.07 <2e-16 ***

Var 2 0.06 25 0.12 5.99 0.01 **

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The ﬁtted model is:

> printCoefmat( coef(summary(yd.glm)), 5)

Estimate Std. Error t value Pr(>|t|)

(Intercept) 1.9687e-03 1.3934e-04 14.1292 2.009e-13 ***

Dens -1.2609e-05 5.1637e-06 -2.4419 0.022026 *

I(1/Dens) 3.5744e-03 4.9364e-04 7.2409 1.376e-07 ***

Var2 1.0015e-04 7.1727e-05 1.3963 0.174914

Var3 2.4503e-04 7.1187e-05 3.4420 0.002041 **

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

While an optimal planting density (in terms of yield per unit area) can be

determined in principle (see Problem 11.6), Fig. 11.11 shows that the optimal

planting density is far beyond the range of the available data in this problem

so will probably be unreliable.

The diagnostics show that the model is adequate (Fig. 11.12):

> library(statmod) # For quantile residuals

> scatter.smooth( rstandard(yd.glm) ~ log(fitted(yd.glm)), las=1,

xlab="Log of fitted values", ylab="Standardized residuals" )

> plot( cooks.distance(yd.glm), type="h", las=1,

ylab="Cook's distance, D" )

> qqnorm( qr <- qresid(yd.glm), las=1 ); qqline(qr)

> plot( rstandard(yd.glm) ~ yieldden$Var, las=1,

xlab="Variety", ylab="Standardized residuals" )

The yield is modelled by a gamma distribution with the same dispersion

parameter for all values of the planting density and all varieties:

> summary(yd.glm)$dispersion

[1] 0.004789151

Since the estimate of φ is small, the saddlepoint approximation will be very

accurate (Sect. 7.5), and the distributional assumptions used in inferences are

accurate also (Sect. 5.4.4).

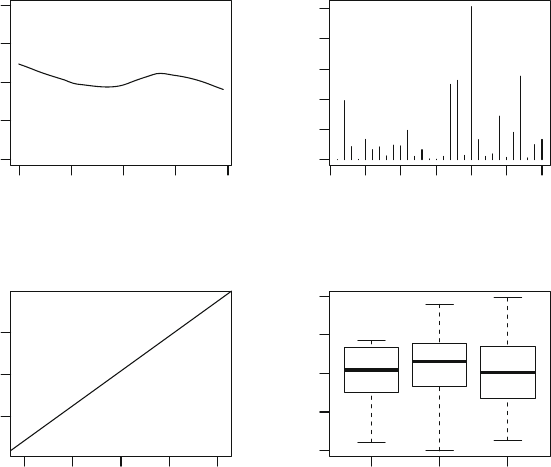
11.9 Summary 445

5.6 5.8 6.0 6.2 6.4

−2

−1

Log of fitted values

Standardized residuals

0 5 10 15 20 25 30

0.00

0.05

0.10

0.15

0.20

0.25

Index

Cook's distance, D

−2 −1 0 1 2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

123

−2

−1

Variety

Standardized residuals

Fig. 11.12 The diagnostic plots from ﬁtting model yd.glm to the yield–density onion

data (Sect. 11.7.2)

11.8 Using R to Fit Gamma and Inverse Gaussian

GLMs

Gamma glms are speciﬁed in r using glm(formula, family=Gamma) in the

glm() call. (Note the capital G, since gamma() refers to the gamma func-

tion Γ ().) Inverse Gaussian glms are speciﬁed in r using glm(family=

inverse.gaussian) (note all lower case) in the glm() call. The link func-

tions "inverse", "identity" and "log" are permitted for both gamma and

inverse Gaussian distributions. The inverse Gaussian distribution also per-

mits the link function "1/mu^2" (the canonical link for the inverse Gaussian

distribution).

11.9 Summary

Chapter 11 considers ﬁtting glms to positive continuous data. Positive

continuous data often have the variance increasing with increasing mean

(Sect. 11.2), so positive continuous data can be modelled using the gamma

446 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

distribution (Sect. 11.3) or, for data more skewed than that suggested by the

gamma distribution, using the inverse Gaussian distribution (Sect. 11.4).

For the gamma distribution (Sect. 11.3), V (μ)=μ

. The residual deviance

D(y, ˆμ) is suitably described by a χ

n−p



distribution if φ ≤ 1/3. For the

inverse Gaussian distribution (Sect. 11.4), V (μ)=μ

. The residual deviance

D(y, ˆμ) is described by a χ

n−p



distribution.

The gamma distribution models the waiting time between events that

occur randomly according to a Poisson distribution (Sect. 11.3). The inverse

Gaussian distribution is related to the ﬁrst-passage time in Brownian motion

(Sect. 11.4).

Commonly-used link functions are the logarithmic, inverse and identity

link functions (Sect. 11.5). Careful choice of the link function and transfor-

mations of the covariates can be used to describe asymptotic relationships

between y and x.

The Pearson estimate of φ is recommended for both the gamma and inverse

Gaussian distributions, though the mle of φ is exact for the inverse Gaussian

distribution (Sect. 11.6).

Problems

Selected solutions begin on p. 544.

11.1. Consider estimating φ for a gamma glm.

1. Prove the result (11.3)(p.436).

2. When w

= 1 for all observations i, show that the mle of φ is the solution

to D(y, ˆμ)=−2n{log φ + ψ(1/φ)}, where ψ(x)=Γ (x)



/Γ (x)isthe

digamma function.

3. Write an r function for computing the mle of φ for a gamma glm

with w

= 1 for all i.(Hint: The digamma function ψ(z) and the

trigamma function ψ

(z)=dψ(z)/dz are available in r as digamma()

and trigamma() respectively.)

4. Using this r function, ﬁnd the mle of φ as given in Example 11.5 (p. 437).

11.2. If a ﬁtted gamma glm includes a constant term and the logarithmic

link function is used, the sum over the observations of the second term

in the expression (11.1) for the residual deviance is zero. In other words,



i=1

− ˆμ

)/ˆμ

= 0. Prove this result by writing the log-likelihood for a

model with linear predictor containing the constant term β

, diﬀerentiating

the log-likelihood with respect to β

, setting to zero and solving.

11.3. Show that the mle of the dispersion parameter φ for an inverse Gaus-

sian distribution is

φ = D(y, ˆμ)/n.

11.4. In this problem we explore the distribution of the unit deviance for the

inverse Gaussian and gamma distributions.

11.9 Summary 447

1. Use r to generate 2000 random numbers y1 from an inverse Gaussian

distribution (using rinvgauss() from the statmod package [7, 26]) with

dispersion=0.1 (that is, φ =0.1). Fit an inverse Gaussian glm with

systematic component y1~1 and then compute the ﬁtted unit deviances

d(y, ˆμ). By using qqplot(), show that these ﬁtted unit deviances follow

a χ

distribution.

2. Use r to generate 2000 random numbers y2 from a gamma distribution

(using rgamma()) with shape=2 and scale=1. (This is equivalent to μ =2

and φ =1/2.) Fit a gamma glm with systematic component y2~1 and

then compute the ﬁtted unit deviances d(y, ˆμ). By using qqplot(), show

that these ﬁtted unit deviances do not follow a χ

distribution.

11.5. Consider the inverse Gaussian distribution (Table 5.1,p.221).

1. Show that the inverse Gaussian distribution with mean μ →∞(called

the Lévy distribution) has the probability function

P(y; φ)=



2πφy

exp{−1/(2yφ)} for y>0.

2. Show that the variance of the Lévy distribution is inﬁnite.

3. Plot the Lévy probability function for φ =0.5andφ =2.

11.6. Show that the maximum value for μ for a gamma glm with a systematic

component of the form 1/μ = β

+ β

x + β

/x occurs at x =



/β

. Then,

show that this maximum value is μ =1/



√



11.7. A study of insurance claims [19] modelled the amount of insurance

claims (for a total of 1975 claims) using a glm(gamma; log) model, with

ﬁve potential qualitative explanatory variables: policy-holder age P (ﬁve age

groups); vehicle type T (ﬁve types); vehicle age V (four age groups); district

D (ﬁve districts); and no-claims discount C (four levels). All main eﬀects are

signiﬁcant, and the interactions are tested using the deviance (Table 11.4).

1. Determine the changes in degrees of freedom after ﬁtting each interaction

term.

2. Find an estimate of the dispersion parameter φ for the model with all

two-factor interactions.

3. Determine which interaction terms are signiﬁcant using likelihood ratio

tests.

4. Interpret the meaning of the interaction term T.P.

11.8. The uk700 randomized trial [1] compared the 2-year costs (in dol-

lars) of treating mentally-ill patients in the community using two diﬀerent

management approaches: intensive (caseload of 10–15 patients) and standard

(caseload of 30–35 patients). Data for 667 patients are available. Numerous

models were ﬁtted, including those summarized in Table 11.5. For all these

models, g(μ)=β

+ β

, where x

= 1 for the intensive group and

is zero otherwise, and x

is the patient age in completed years.

448 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

Table 11.4 The analysis of deviance table from ﬁtting a gamma glm to claim severity

data; read down the columns (Problem 11.7)

Terms Residual deviance Terms Residual deviance

Main eﬀects model 5050.9

+ T.P 4695.2 + P.D 4497.1

+ T.V 4675.9 + P.C 4462.0

+ T.D 4640.1 + V.D 4443.4

+ T.C 4598.8 + V.C 4420.8

+ P.V 4567.3 + D.C 4390.9

Table 11.5 Summaries of the glms ﬁtted to the mental care cost data [1, Table 3],

using identity and logarithmic link functions (Problem 11.8)

edm g(μ)

95% ci

95% ci aic

Normal Identity 2032 (−1371, 5435) −3324 (−4812, −1836) 15, 259

Gamma Identity 1533 (−1746, 4813) −2622 (−3975, −1270) 14, 765

Inverse Gaussian Identity 1361 (−1877, 4601) −2416 (−3740, −1091) 15, 924

Normal Log 1.10 (0.95, 1.27) 0.84 (0.79, 0.90) 15, 256

Gamma Log 1.07 (0.93, 1.24) 0.88 (0.82, 0.93) 14, 763

Inverse Gaussian Log 1.07 (0.93, 1.23) 0.89 (0.84, 0.95) 15, 924

1. Based on the aic,whichedm seems most appropriate?

2. The constants in the models β

are not revealed. Nonetheless, write down

the two models based on this edm as comprehensively as possible.

3. Interpret the regression parameters for x

in both models.

4. Interpret the regression parameters for x

in both models.

5. Is the type of treatment signiﬁcant for modelling cost? Explain.

6. Is the patient age signiﬁcant for modelling cost? Explain.

7. Which interpretation (i.e. the use of which link function) seems most

appropriate? Why?

11.9. For the small-leaved lime data in data set lime, the gamma glm lime.

log was ﬁtted in Example 11.6 (p. 438). Consider ﬁtting a similar gamma

glm with a log link, but using DBH as the explanatory variable in place of

log(DBH).

1. Produce the diagnostic plots for this model.

2. Interpret the ﬁtted model.

3. Do the diagnostic plots suggest which model (using DBH or log(DBH))is

preferred?

11.10. For the small-leaved lime data in data set lime, the model in

Example 11.1 proposed a relationship between Foliage and log(DBH).

Determine if a model that also includes Age improves the model.

11.9 Summary 449

Table 11.6 The average daily fat yields (in kg/day) each week for 35 weeks for a dairy

cow (Problem 11.12)

Week Yield Week Yield Week Yield Week Yield Week Yield

1 0.31 8 0.66 15 0.57 22 0.30 29 0.15

2 0.39 9 0.67 16 0.48 23 0.26 30 0.18

30.50 100.70 170.46 240.34 310.11

40.58 110.72 180.45 250.29 320.07

50.59 120.68 190.31 260.31 330.06

60.64 130.65 200.33 270.29 340.01

70.68 140.64 210.36 280.20 350.01

11.11. For the small-leaved lime data in data set lime, the model in

Example 11.1 proposed that the coeﬃcient for log(DBH) was expected

to be approximately 2. For this problem, consider ﬁtting a gamma glm with

only log(DBH) as an explanatory variable (that is, without Origin)totest

this idea.

1. Test this hypothesis using a Wald test, and comment.

2. Test this hypothesis using a likelihood ratio test, and comment.

11.12. In the dairy science literature, Wood’s lactation curve is the equation,

justiﬁed biometrically, relating the production of milk fat y in week t:

y = at

exp(ct),

where the parameters a, b and c are estimated from the data. Lactation

data [10] from one dairy cow are shown in Table 11.6 (data set: lactation).

1. Plot the data, and propose possible models based on the graphs shown

in Sect. 11.5.

2. Fit models suggested above, plus the model suggested by Wood’s lacta-

tion curve.

3. Plot the curves on the data, and comment.

11.13. A study of computer tomography (ct) interventions [23, 32] in the ab-

domen measured the total procedure time (in s) and the total radiation dose

received (in rads) (Table 3.21; data set: fluoro). During these procedures,

“one might postulate that the radiation dose received is related to. . . the total

procedure time” [32, p. 61].

1. Find a suitable glm for the data, ensuring a diagnostic analysis, and test

the hypothesis implied by the above quotation.

2. Plot the ﬁtted model, including the 95% conﬁdence interval about the

ﬁtted line.

11.14. Nambe Mills, Santa Fe, New Mexico [3, 25], is a tableware manu-

facturer. After casting, items produced by Nambe Mills are shaped, ground,

450 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

buﬀed, and polished. In 1989, as an aid to rationalizing production of its 100

products, the company recorded the total grinding and polishing times and

the diameter of each item (Table 5.3; data set: nambeware). In Chaps. 5–8

(Problems 5.26, 6.11, 7.5 and 8.12), only the item diameter was considered

as an explanatory variable. Now, consider modelling price y as a function of

all explanatory variables.

1. Plot the Price against Type, against Diam and against Time.Whatdothe

plots suggest about the relationship between the mean and the variance

for the data?

2. What possible distribution could be used to ﬁt a glm? Justify your an-

swer.

3. Determine a good model for Price, considering interactions. Perform a

comprehensive diagnostic test of your model and comment on the struc-

ture of the ﬁtted model.

4. Write down your ﬁnal model(s).

5. Interpret your ﬁnal model(s).

11.15. The lung capacity data [13] in Example 1.1 have been used in Chaps. 2

and 3 (data set: lungcap).

1. Plot the data, and identify possible relationships between FEV and the

other variables.

2. Find a suitable glm for the data, ensuring a diagnostic analysis.

3. Is there evidence that smoking aﬀects lung capacity?

4. Interpret your model.

11.16. In a study of foetal size [20], the mandible length (in mm) and gesta-

tional age (in weeks) for 167 foetuses were measured from the 12th week

of gestation onwards (Table 11.7; data set: mandible). According to the

source [20, p. 437], the data for foetuses aged over 28 weeks should be dis-

carded, because “the technique was diﬃcult to perform and excessive mea-

surement error was suspected”.

1. Using the subset() command in r, create a data frame of the measure-

ments for the 158 foetuses less than or equal to 28 weeks.

Table 11.7 The mandible length and foetal age (Problem 11.16)

Age (in weeks) Length (in mm)

12.3 8

12.4 9

12.7 11

12.9 10

11.9 Summary 451

2. Plot this data subset, and identify the important features of the data.

3. Fit a suitable model for the data subset. Consider exploring diﬀerent link

functions, and including polynomial terms in age.

4. Plot the full data set (including foetuses older than 28 weeks of age), and

then draw the systematic component on the same plot. Does the model

ﬁt well to these extra observations?

5. Find and interpret the 90% Wald conﬁdence interval for the age param-

eter.

11.17. The times to death (in weeks) of two groups of leukaemia patients

whose white blood cell counts were measured (Table 4.3; data set: leukwbc)

were grouped according to a morphological variable called the ag factor [5].

1. Plot the survival time against white blood cell count (wbc), distinguish-

ing between ag-positive and ag-negative patients. Comment on the re-

lationship between wbc and survival time, and the ag factor.

2. Plot the survival time against log

wbc, and argue that using log

wbc

is likely to be a better choice as an explanatory variable.

3. Fit a glm(gamma; log) model to the data, including the interaction term

between the ag factor and log

wbc, and show that the interaction term

is not necessary.

4. Reﬁt the glm without the interaction term, and evaluate the model using

diagnostic tools.

5. Plot the ﬁtted lines for each ag-factor on a plot of the observations.

6. The original source [5] uses an exponential distribution (4.37), which is

a gamma distribution with φ = 1. Does this seem reasonable?

11.18. The data in Table 11.8 come from a study [14] of the nitrogen content

of soil, with three replicates at each dose (data set: nitrogen).

1. Plot the data, identifying the organic nitrogen source.

Table 11.8 The soil nitrogen (in kilograms of nitrogen per hectare) after applying

diﬀerent doses of fertilizer (in kilograms of nitrogen per hectare). The fertilizers are in-

organic apart from the dose of 248 kg N ha

−1

, whose source is organic (farmyard manure)

(Problem 11.18)

Fertilizer dose Soil N content

Control 4.53 5.46 4.77

48 6.17 9.30 8.29

96 11.30 16.58 16.24

144 24.61 18.20 30.03

192 21.94 29.24 27.43

240 46.74 38.87 44.07

288 57.74 45.59 39.77

248 25.28 21.79 19.75

452 11 Positive Continuous Data: Gamma and Inverse Gaussian GLMs

2. Find the mean and variance of each fertilizer dose. Then, plot the loga-

rithm of the variance against the logarithm of the means, and show that

a gamma distribution appears sensible.

3. Fit a suitable gamma glm to the data, including a diagnostic analysis.

11.19. In Problem 2.18 (p. 88), data are given from an experiment where

children were asked to build towers out of cubical and cylindrical blocks as

high as they could [11, 24]. The number of blocks used and the time taken

were recorded (Table 2.12; data set: blocks). In this problem, we examine

the time taken to stack blocks.

1. Find a suitable gamma glm for modelling the time taken to build the

towers.

2. Find a suitable inverse Gaussian glm for modelling the time taken to

build the towers.

3. Using a diagnostic analysis, determine which of the two models is more

appropriate.

4. Test the hypothesis that the time taken to stack the blocks diﬀers between

cubical and cylindrical shaped blocks.

5. Test the hypothesis that older children take less time to stack the blocks,

for both cubes and cylinders.

11.20. Hardness of timber is diﬃcult to measure directly, but is related to

the density of the timber (which is easier to measure). To study this rela-

tionship [29], density and Janka hardness measurements for 36 Australian

eucalyptus hardwoods were obtained (Table 11.9; data set: hardness). Ven-

ables [27] suggests that a glm using a square-root link function with a gamma

distribution ﬁts the data well. Fit the suggested model, and use a diagnostic

analysis to show that this model seems reasonable.

Table 11.9 The Janka hardness and density of Australian hardwoods, units unknown

(Problem 11.20)

Density Hardness Density Hardness Density Hardness

24.7 484 39.4 1210 53.4 1880

24.8 427 39.9 989 56.0 1980

27.3 413 40.3 1160 56.5 1820

28.4 517 40.6 1010 57.3 2020

28.4 549 40.7 1100 57.6 1980

29.0 648 40.7 1130 59.2 2310

30.3 587 42.9 1270 59.8 1940

32.7 704 45.8 1180 66.0 3260

35.6 979 46.9 1400 67.4 2700

38.5 914 48.2 1760 68.8 2890

38.8 1070 51.5 1710 69.1 2740

39.3 1020 51.5 2010 69.1 3140

11.9 Summary 453

11.21. In Problem 3.19, a study of urethral length L and mass M of various

mammals [30] was discussed. For these data (data set: urinationL), one

postulated relationship is L = kM

1/3

for some proportionality constant k.

In that Problem, a weighted regression model was ﬁtted to the data using a

transformation of the relationship to linearity: log L = log k + (log M)/3. Fit

an approximately-equivalent glm for modelling these data. Using this model,

test the hypothesis again using both a Wald and likelihood-ratio test.

11.22. In Problem 3.11 (p. 150), data are given from a study of the food

consumption of ﬁsh [17] (data set: fishfood). In Problem 3.11, the linear

regression model ﬁtted in the source is shown. Fit the equivalent gamma

glm for modelling the daily food consumption, and compare to the linear

regression model in Problem 3.11.

11.23. In Problem 3.17, the daily energy requirements [9, 28, 31] and weight

of 64 wethers (Table 2.11; data set: sheep) were analysed using a linear

regression model, using the logarithm of the daily energy requirements as the

response.

1. Fit the equivalent glm.

2. Perform a diagnostic analysis of the glm and compare to the regres-

sion model using the logarithm of the daily energy requirements as the

response. Comment.

3. Plot the data and the ﬁtted glm, and add the 95% conﬁdence intervals

for the ﬁtted values.

4. Interpret the glm.

11.24. An experiment to investigate the initial rate of benzene oxidation [18]

over a vanadium oxide catalyst used three diﬀerent reaction temperatures and

varied oxygen and benzene concentrations. A subset of the data is presented

in Table 11.10 (data set: rrates) for a benzene concentration near 2 ×10

−3

gmoles/L.

1. Plot the reaction rate against oxygen concentration, distinguishing dif-

ferent temperatures. What important features of the data are obvious?

2. Compare the previous plot to Fig. 11.8 (p. 436) and Fig. 11.9 (p. 437).

Suggest two functional relationships between oxygen concentration and

reaction rate that could be compared.

3. Fit the models identiﬁed above, and separately plot the ﬁtted systematic

components on the data. Select a model, explaining your choice.

4. For your chosen model, perform a diagnostic analysis, identifying poten-

tial problems with the model.

5. By looking at the data for each temperature separately, is it reasonable to

assume the dispersion parameter φ is approximately constant? Explain.

454 REFERENCES

Table 11.10 The initial reaction rate of benzene oxidation. Oxygen concentration [O]

is ×10

gmole/L; the temperature is in Kelvin; and the reaction rate is ×10

gmole/g

of catalyst/s (Problem 11.24)

Temp: 623 K Temp: 648 K Temp: 673 K

[O] Rate [O] Rate [O] Rate

134.5 218 23.3 229 16.0 429

108.0 189 40.8 296 23.5 475

68.6 192 140.3 547 132.8 1129

49.5 174 140.8 582 107.7 957

41.7 152 141.2 480 68.5 745

29.4 139 140.0 493 47.2 649

22.5 118 121.2 513 42.5 742

17.2 120 104.7 411 30.1 662

17.0 122 40.8 349 11.2 373

22.8 132 22.5 226 17.1 440

41.3 167 55.2 338 65.8 662

59.6 208 55.4 351 108.2 724

119.7 216 29.5 295 123.5 915

158.2 294 30.0 294 160.0 944

16.3 233 66.4 713

16.5 222 66.5 736

20.8 239

20.6 217

References

[1] Barber, J., Thompson, S.: Multiple regression of cost data: Use of gen-

eralized linear models. Journal of Health Services Research and Policy

9(4), 197–204 (2004)

[2] Crawley, M.J.: Glim for Ecologists. Blackwell Scientiﬁc Publications,

London (1993)

[3] Data Desk: Data and story library (dasl) (2017). URL http://dasl.

datadesk.com

[4] Dunn, P.K., Smyth, G.K.: Randomized quantile residuals. Journal of

Computational and Graphical Statistics 5(3), 236–244 (1996)

[5] Feigl, P., Zelen, M.: Estimation of exponential survival probabilities with

concomitant information. Biometrics 21, 826–838 (1965)

[6] Fox, R., Garbuny, M., Hooke, R.: The Science of Science. Walker and

Company, New York (1963)

[7] Giner, G., Smyth, G.K.: statmod: probability calculations for the inverse

Gaussian distribution. The R Journal 8(1), 339–351 (2016)

[8] Hald, A.: Statistical Theory with Engineering Applications. John Wiley

and Sons, New York (1952)

[9] Hand, D.J., Daly, F., Lunn, A.D., McConway, K.Y., Ostrowski, E.: A

Handbook of Small Data Sets. Chapman and Hall, London (1996)

REFERENCES 455

[10] Henderson, H.V., McCulloch, C.E.: Transform or link? Tech. Rep. BU-

049-MA, Cornell University (1990)

[11] Johnson, B., Courtney, D.M.: Tower building. Child Development 2(2),

161–162 (1931)

[12] Jørgensen, B.: Exponential dispersion models and extensions: A review.

International Statistical Review 60(1), 5–20 (1992)

[13] Kahn, M.: An exhalent problem for teaching statistics. Journal of Sta-

tistical Education 13(2) (2005)

[14] Lane, P.W.: Generalized linear models in soil science. European Journal

of Soil Science 53, 241–251 (2002)

[15] McCullagh, P., Nelder, J.A.: Generalized Linear Models, second edn.

Monographs on Statistics and Applied Probability. Chapman and Hall,

London (1989)

[16] Mead, R.: Plant density and crop yield. Applied Statistics 19(1), 64–81

(1970)

[17] Palomares, M.L., Pauly, D.: A multiple regression model for predicting

the food consumption of marine ﬁsh populations. Australian Journal of

Marine and Freshwater Research 40(3), 259–284 (1989)

[18] Pritchard, D.J., Downie, J., Bacon, D.W.: Further consideration of het-

eroscedasticity in ﬁtting kinetic models. Technometrics 19(3), 227–236

(1977)

[19] Renshaw, A.E.: Modelling the claims process in the presence of covari-

ates. ASTIN Bulletin 24(2), 265–285 (1994)

[20] Royston, P., Altman, D.G.: Regression using fractional polynomials of

continuous covariates: Parsimonious parametric modelling. Journal of

the Royal Statistical Society, Series C 43(3), 429–467 (1994)

[21] Schepaschenko, D., Shvidenko, A., Usoltsev, V.A., Lakyda, P., Luo, Y.,

Vasylyshyn, R., Lakyda, I., Myklush, Y., See, L., McCallum, I., Fritz,

S., Kraxner, F., Obersteiner, M.: Biomass plot data base. PANGAEA

(2017). DOI 10.1594/PANGAEA.871465. In supplement to: Schep-

aschenko, D et al. (2017): A dataset of forest biomass structure for

Eurasia. Scientiﬁc Data, 4, 170070, doi:10.1038/sdata.2017.70

[22] Schepaschenko, D., Shvidenko, A., Usoltsev, V.A., Lakyda, P., Luo, Y.,

Vasylyshyn, R., Lakyda, I., Myklush, Y., See, L., McCallum, I., Fritz,

S., Kraxner, F., Obersteiner, M.: A dataset of forest biomass structure

for Eurasia. Scientiﬁc Data 4, 1–11 (2017)

[23] Silverman, S.G., Tuncali, K., Adams, D.F., Nawfel, R.D., Zou, K.H.,

Judy, P.F.: ct ﬂuoroscopy-guided abdominal interventions: Techniques,

results, and radiation exposure. Radiology 212, 673–681 (1999)

[24] Singer, J.D., Willett, J.B.: Improving the teaching of applied statistics:

Putting the data back into data analysis. The American Statistician

44(3), 223–230 (1990)

[25] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

456 REFERENCES

[26] Smyth, G.K.: statmod: Statistical Modeling (2017). URL https://

CRAN.R-project.org/package=statmod. R package version 1.4.30. With

contributions from Yifang Hu, Peter Dunn, Belinda Phipson and Yun-

shun Chen.

[27] Venables, W.N.: Exegeses on linear models. In: S-Plus User’s Conference.

Washington DC (1998). URL https://www.stats.ox.ac.uk/pub/MASS3/

Exegeses.pdf

[28] Wallach, D., Goﬃnet, B.: Mean square error of prediction in models for

studying ecological systems and agronomic systems. Biometrics 43(3),

561–573 (1987)

[29] Williams, E.J.: Regression Analysis. Wiley, New York (1959)

[30] Yang, P.J., Pham, J., Choo, J., Hu, D.L.: Duration of urination does not

change with body size. Proceedings of the National Academy of Sciences

111(33), 11 932–11 937 (2014)

[31] Young, B.A., Corbett, J.L.: Maintenance energy requirement of grazing

sheep in relation to herbage availability. Australian Journal of Agricul-

tural Research 23(1), 57–76 (1972)

[32] Zou, K.H., Tuncali, K., Silverman, S.G.: Correlation and simple linear

regression. Radiology 227, 617–628 (2003)

Chapter 12

Tweedie GLMs

...we cannot know if any statistical technique that we

develop is useful unless we use it.

Box [5, p. 792]

12.1 Introduction and Overview

This chapter introduces glms based on Tweedie edms. Tweedie edm sare

distributions that generalize many of the edms already seen (the normal,

Poisson, gamma and inverse Gaussian distributions are special cases) and

include other distributions also. First, Tweedie edms are discussed in general

(Sect. 12.2), and then two subsets of the Tweedie glms which are impor-

tant are studied: Tweedie edms for modelling positive continuous data for

which gamma and inverse Gaussian glms are special cases (Sect. 12.2.3), then

Tweedie edms for modelling continuous data with exact zeros (Sect. 12.2.4).

We then follow with a description of how to use these Tweedie edmstoﬁt

Tweedie glms (Sect. 12.3).

12.2 The Tweedie EDMs

12.2.1 Introducing Tweedie Distributions

Apart from the binomial and negative binomial distributions, the edms seen

so far in this book have variance functions with similar forms:

• the normal distribution, where V (μ)=μ

= 1 (Chaps. 2 and 3);

• the Poisson distribution, where V (μ)=μ

(Chap. 10);

• the gamma distribution, where V (μ)=μ

(Chap. 11);

• the inverse Gaussian distribution, where V (μ)=μ

(Chap. 11).

These edms have power variance functions of the form V (μ)=μ

, with

ξ =0, 1, 2, 3. More generally, any edm with a variance function V (μ)=μ

called a Tweedie distribution,oraTweedie edm, where ξ can take any real

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_12

457

458 12 Tweedie GLMs

Table 12.1 Features of the Tweedie distributions for various values of the index param-

eter ξ, showing the support S (the permissible values of y) and the domain Ω for μ.The

Poisson distribution (ξ =1andφ = 1) is a special case of the discrete distributions, and

the inverse Gaussian distribution (ξ = 3) is a special case of positive stable distributions.

R refers to the real line; superscript + means positive real values only; subscript 0 means

zero is included in the space (Sect. 12.2.1)

Tweedie edm ξSΩReference

Extreme stable ξ<0 RR

Not covered

Normal ξ =0 RRChaps. 2 and 3

No edmsexist 0<ξ<1

Discrete ξ =1 y =0,φ,2φ,... R

Chap. 10 for φ =1

Poisson-gamma 1 <ξ<2 R

Sect. 12.2.3

Gamma ξ =2 R

Chap. 11

Positive stable ξ>2 R

Sect. 12.2.4

value except 0 <ξ<1[25]. ξ is called the Tweedie index parameter and is

sometimes denoted by p. This power-variance relationship has been observed

in natural populations for many years [36, 37]. Useful information about the

Tweedie distribution appears in Table 5.1 (p. 221).

The four speciﬁc cases of Tweedie distributions listed above show that the

Tweedie distributions are useful for a variety of data types (Table 12.1). More

generally:

•Forξ ≤ 0, the Tweedie distributions are suitable for modelling continuous

data where −∞ <y<∞. The normal distribution (ξ = 0) is a special

case. When ξ<0, the Tweedie distributions have the unusual feature

that data y are deﬁned on the entire real line, but μ>0. These Tweedie

distributions with ξ<0 have no known realistic applications, and so are

not considered further.

•Forξ = 1 the Tweedie distributions are suitable for modelling discrete

data where y =0,φ,2φ, 3φ,.... When φ = 2, for example, a positive

probability exists for y =0, 2, 4,.... The Poisson distribution is a special

case when φ =1.

•For1<ξ<2, the Tweedie distributions are suitable for modelling

positive continuous data with exact zeros. An example is rainfall mod-

elling [12, 31]: when no rain falls, an exact zero is recorded, but when

rain does fall, the amount is a continuous measurement. Plots of example

probability functions are shown in Fig. 12.1.Asξ → 1, the densities show

local maxima corresponding to the discrete masses for the corresponding

Poisson distribution.

•Forξ ≥ 2, the Tweedie distributions are suitable for modelling positive

continuous data. The gamma (

ξ = 2) and inverse Gaussian (ξ =3)

distributions are special cases (Chap. 11). The distributions become more

right skewed as ξ increases (Fig. 12.2).

12.2 The Tweedie EDMs 459

ξ=1.05

Density

01234

ξ=1.2

Density

01234

φ=0.5

φ=1

ξ=1.6

Density

01234

Fig. 12.1 Examples of Tweedie probability functions with 1 <ξ<2andμ =1.The

solid lines correspond to φ =0.5 and the dotted lines to φ = 1. The ﬁlled dots show the

probability of exactly zero when φ =0.5 and the empty squares show the probability of

exactly zero when φ = 1 (Sect. 12.2.1)

ξ=2.5

Density

01234

ξ=3.5

Density

01234

φ=0.5

φ=1

ξ=5

Density

01234

Fig. 12.2 Examples of Tweedie probability functions with ξ>2andμ =1.Asξ gets

larger, the distributions become more skewed to the right. The solid lines correspond to

φ =0.5; the dotted lines to φ = 1 (Sect. 12.2.1)

ξ is called the Tweedie index parameter for the Tweedie distributions, and

speciﬁes the particular distribution in the Tweedie family of distributions.

The two cases 1 <ξ<2andξ ≥ 2 are considered in this chapter in further

detail. (The special cases ξ =0, 1, 2, 3 were considered earlier.)

460 12 Tweedie GLMs

12.2.2 The Structure of Tweedie EDMs

Tweedie distributions are deﬁned as edms with variance function V (μ)=μ

for some given ξ. Using this relationship, θ and κ(θ) can be determined (fol-

lowing the ideas in Sect. 5.3.6). Setting the arbitrary constants of integration

to zero, obtain (Problem 12.1)

θ =

⎧

⎪

⎨

⎪

⎩

1−ξ

1 − ξ

for ξ =1

log μ for ξ =1

and κ(θ)=

⎧

⎪

⎨

⎪

⎩

2−ξ

2 − ξ

for ξ =2

log μ for ξ =2

. (12.1)

Other parameterizations are obtained by setting the constants of integration

to other values. One useful parameterization ensures θ and κ(θ) are con-

tinuous functions of ξ [16] (Problem 12.2). The expressions for θ and κ(θ)

contain ξ, so the Tweedie distributions are only edmsifξ is known. In prac-

tice, the value of ξ is usually estimated (Sect. 12.3.2). If y follows a Tweedie

distribution with index parameter ξ, mean μ and dispersion parameter φ,

write y ∼ Tw

(μ, φ).

Based on these expressions for θ and κ(θ), the Tweedie probability function

may be written in canonical form (5.1). Apart from the special cases identiﬁed

earlier (the normal, Poisson, gamma and inverse Gaussian distributions), the

normalizing constant a(y, φ) cannot be written in closed form. Consequently,

accurate evaluation of the probability function for Tweedie edms in general

requires numerical methods [15, 16].

The unit deviance is (Problem 12.3)

d(y, μ)=

⎧

⎪

⎨

⎪

⎩



max(y, 0)

2−ξ

(1 − ξ)(2 − ξ)

−

yμ

1−ξ

1 − ξ

2−ξ

2 − ξ



for ξ =1, 2;



y log

− (y − μ)



for ξ =1;



−log

y −μ



for ξ =2.

(12.2)

When y = 0, the unit deviance is ﬁnite for ξ ≤ 0 and 1 <ξ<2. (Recall

y = 0 is only admitted for ξ ≤ 0 and 1 <ξ<2; see Table 12.1.)

The Tweedie probability function can be written in the form of a dispersion

model (5.13) also, using the unit deviance (12.2). In this form, the normalizing

constant b(y, φ) cannot be written in closed form, apart from the four special

cases. By the saddlepoint approximation, D(y, ˆμ) ∼ χ

n−p



approximately for

a model with p



parameters in the linear predictor. The saddlepoint approx-

imation is adequate if φ ≤ min{y}

2−ξ

/3 for the cases ξ ≥ 1 considered in

this chapter (Prob. 12.4). One consequence of this is that the approximation

12.2 The Tweedie EDMs 461

is likely to be poor if any y = 0 (when 1 <ξ<2). Also, recall that ξ =3

corresponds to the inverse Gaussian distribution, for which the saddlepoint

approximation is exact.

Of interest is the Tweedie rescaling identity [16]. Writing P

(y; μ, φ)for

the probability function of a Tweedie edm with index parameter ξ, then

(y; μ, φ)=cP

(cy; cμ, c

2−ξ

φ) (12.3)

for all ξ, where y>0andc>0.

12.2.3 Tweedie EDMs for Positive Continuous Data

In most situations, positive continuous responses are adequately modelled

using a gamma or inverse Gaussian distribution (Chap. 11). In some circum-

stances, neither is adequate, especially for severely skewed data. However,

all edms with variance functions of the form μ

for ξ ≥ 2 are suitable for

positive continuous data. The gamma (ξ = 2) and inverse Gaussian (ξ =3)

distributions are just two special cases, and are the only examples of Tweedie

edms with ξ ≥ 2 with probability functions that can be written in closed

form. One important example corresponds to V (μ)=μ

, which is approxi-

mately equivalent to using the transformation 1/y as the response variable

in a linear regression model.

Example 12.1. The survival times (in 10 h units) of animals subjected to three

types of poison were measured [6] for four diﬀerent treatments (Table 12.2;

data set: poison). Four animals were used for each poison–treatment combi-

nation (Fig. 12.3, top panels):

> data(poison); summary(poison)

Psn Trmt Time

I :16 A:12 Min. :0.1800

II :16 B:12 1st Qu.:0.3000

III:16 C:12 Median :0.4000

D:12 Mean :0.4794

3rd Qu.:0.6225

Max. :1.2400

Table 12.2 Survival times (in 10 h units) for animals under four treatments A, B, C

and D, and three poison types I, II and III (Example 12.1)

Poison I Poison II Poison III

ABCD ABCD ABCD

0.31 0.82 0.43 0.45 0.36 0.92 0.44 0.56 0.22 0.30 0.23 0.30

0.45 1.10 0.45 0.71 0.29 0.61 0.35 1.02 0.21 0.37 0.25 0.36

0.46 0.88 0.63 0.66 0.40 0.49 0.31 0.71 0.18 0.38 0.24 0.31

0.43 0.72 0.76 0.62 0.23 1.24 0.40 0.38 0.23 0.29 0.22 0.33

462 12 Tweedie GLMs

I II III

0.2

0.4

0.6

0.8

1.0

1.2

Poison type

Time

ABCD

0.2

0.4

0.6

0.8

1.0

1.2

Treatment type

Time

Poison type

Mean time

I II III

0.0

0.2

0.4

0.6

0.8

1.0

1.2

T'ment A

T'ment B

T'ment C

T'ment D

−1.6 −1.2 −0.8 −0.4

−8

−7

−6

−5

−4

−3

−2

log(sample means)

log(sample variances)

slope = 3.95

Fig. 12.3 The poison data. The time to death plotted against poison type (top left

panel); the time to death plotted against treatment type (top right panel); the mean of

the time to death by poison type and treatment type (bottom left panel); the logarithm

of each treatment–poison group variance plotted against the logarithm of the group

means (bottom right panel) (Example 12.1)

> plot( Time ~ Psn, xlab="Poison type", las=1, data=poison )

> plot( Time ~ Trmt, xlab="Treatment type", las=1, data=poison )

> GroupMeans <- tapply(poison$Time, list(poison$Psn, poison$Trmt), "mean")

> matplot( GroupMeans, type="b", xlab="Poison type", ylab="Mean time",

pch=1:4, col="black", lty=1:4, lwd=2, ylim=c(0, 1.3), axes=FALSE)

> axis(side=1, at=1:3, labels=levels(poison$Psn))

> axis(side=2, las=1); box()

> legend("topright", lwd=2, lty=1:4, ncol=2, pch=1:4,

legend=c("T'ment A", "T'ment B", "T'ment C", "T'ment D"))

Finding the variance and the mean of the four observations in each poison–

treatment combination and plotting (Fig. 12.3, bottom right panel) shows

that the variance is a function of the mean:

> # Find mean and var of each poison/treatment combination

> mns <- tapply(poison$Time, list(poison$Psn, poison$Trmt), mean)

12.2 The Tweedie EDMs 463

> vrs <- tapply(poison$Time, list(poison$Psn, poison$Trmt), var)

> # Plot

> plot( log(c(vrs)) ~ log(c(mns)), las=1, pch=19,

xlab="log(sample means)", ylab="log(sample variances)")

> mvline <- lm( log( c(vrs) ) ~ log( c(mns) ) )

> slope <- round( coef( mvline )[2], 2); abline( mvline, lwd=2)

> slope

log(c(mns))

3.95

The slope of this line is 3.95, suggesting a Tweedie edm with ξ ≈ 4maybe

appropriate. 

12.2.4 Tweedie EDMs for Positive Continuous Data

with Exact Zeros

Tweedie edms with 1 <ξ<2 are useful for modelling continuous data with

exact zeros. An example of this type of data is insurance claims data [26,

34]. Assume N claims are made in a particular company in a certain time

frame, where N ∼ Pois(λ

∗

) where λ

∗

is the Poisson mean number of claims

in the time frame. Observe that N could be zero if no claims are made.

When N>0, assume the amount of each claim i =1,...,N is z

, where

must be positive. Assume z

follows a gamma distribution with mean μ

∗

and dispersion parameter φ

∗

,sothatz

∼ Gam(μ

∗

,φ

∗

). The total insurance

payout y is the sum of the N individual claims, such that

y =



i=1

where y = 0 when N = 0. The total claim amount y has a Tweedie distri-

bution with 1 <ξ<2. In this interpretation, y is a Poisson sum of gamma

distributions, and hence these Tweedie distributions with 1 <ξ<2 are some-

times called Poisson–gamma distributions [31], though this term sometimes

has another, but related, meaning [17].

Example 12.2. The Quilpie rainfall data were considered in Example 4.6 (data

set: quilpie), where the probability of observing at least 10 mm of total

July rainfall was the quantity of interest. In this example, we examine the

total July rainfall in Quilpie. Observe that the total monthly July rainfall is

continuous, with exact zeros:

> library(GLMsData); data(quilpie)

> head(quilpie)

Year Rain SOI Phase Exceed y

1 1921 38.4 2.7 2 Yes 1

2 1922 0.0 2.0 5 No 0

464 12 Tweedie GLMs

3 1923 0.0 -10.7 3 No 0

4 1924 24.4 6.9 2 Yes 1

5 1925 0.0 -12.5 3 No 0

6 1926 9.1 -1.0 4 No 0

> sum( quilpie$Rain==0 ) # How many months with exactly zero rainfall?

[1] 20

For these data, a Tweedie distribution with 1 <ξ<2 may be appropriate.

The monthly rainfall could be considered as a Poisson sum of rainfall events

each July, with each event producing rainfall amounts that follow a gamma

distribution. 

The parameters of the ﬁtted Tweedie edm deﬁned in Sect. 12.2.2, namely

μ, φ and ξ, are related to the parameters of the underlying Poisson and

gamma distributions by

∗

2−ξ

φ(2 − ξ)

;

∗

=(2− ξ)φμ

ξ−1

; (12.4)

∗

=(2− ξ)(ξ − 1)φ

2(ξ−1)

Tweedie edms with 1 <ξ<2 are continuous for y>0, but have a positive

probability π

at y = 0, where [15]

=Pr(y = 0) = exp(−λ

∗

) = exp



−

2−ξ

φ(2 − ξ)



. (12.5)

To compute the mle of π

,themlesofμ, ξ and φ must be used in (12.5)

(see the ﬁrst property of mles in Sect. 4.9). The mlesofμ, ξ and φ can be

computed in r as shown in Sect. 12.3.2.

After computing the mlesofμ, φ and ξ,themlesofλ

∗

, μ

∗

and φ

∗

can be

computed using (12.4). These estimates give an approximate interpretation

of the model based on the underlying Poisson and gamma models [7, 12, 15],

and may sometimes be useful (see Sect. 12.7).

12.3 Tweedie GLMs

12.3.1 Introduction

Glms based on the Tweedie distributions are Tweedie glms, speciﬁed as

glm(Tweedie, ξ; Link function). For both cases considered in this chapter

(that is, ξ>2 and 1 <ξ<2), we have μ>0 (Table 12.1). As a result, the

usual link function used for Tweedie glms is the logarithmic link function.

The dispersion parameter φ is usually estimated using the Pearson estimate

12.3 Tweedie GLMs 465

(though the mle of φ is necessary for computing the mle of the probability

of exact zeros when 1 <ξ<2, as explained in Sect. 12.2.4).

To ﬁt Tweedie glms, the particular distribution in the Tweedie family must

be speciﬁed by deﬁning the value of ξ, but usually the value of ξ is unknown

and must be estimated before the Tweedie glm is ﬁtted (Sect. 12.3.2). The

correlation between

ξ and

β is small, so using the estimate

ξ has only a small

eﬀect on inference concerning β compared to knowing the true value of ξ.

Linear regression models using a Box–Cox transformation of the responses

can be viewed as an approximation to the Tweedie glm with the same under-

lying mean–variance relationship (Problem 12.7); see Sect. 5.8 (p. 232)and

Table 5.2. In terms of inference, the normal approximation to the Box–Cox

transformed responses can be quite poor when the responses cover a wide

range, especially when the responses include exact zeros or near zeros. As a

result, the Tweedie glm approach can often give superior results.

12.3.2 Estimation of the Index Parameter ξ

As noted, ﬁtting a Tweedie glm requires that the value of the index pa-

rameter ξ be known, which identiﬁes the speciﬁc Tweedie edm to use. Since

Tweedie distributions are deﬁned as edms with var[y]=φV (μ)=φμ

, then

log(var[y]) = log φ + ξ log μ. This shows that a simplistic method for esti-

mating ξ is to divide the data into a small number of groups, and plot the

logarithm of the group variances against the logarithm of the group means,

as used in Example 12.1 and Example 5.9 (the noisy miner data). However,

the estimate of ξ may depend upon how the data are divided.

Note that if exact zeros are present in the data, then 1 <ξ<2. However,

if the data contains no exact zeros, then ξ ≥ 2 is common but 1 <ξ<2

is still possible. In this situation, one interpretation is that exact zeros are

feasible but simply not observed in the given data (Example 12.7).

Example 12.3. For the Quilpie rainfall data (data set: quilpie), the mean and

variance of the monthly July rainfall amounts can be computed within each

soi phase, and the slope computed. An alternative approach is to compute

the mean and variance of the rainfall amounts within each decade:

> # Group by SOI Phase

> mn <- with( quilpie, tapply( Rain, Phase, "mean"))

> vr <- with( quilpie, tapply( Rain, Phase, "var"))

> coef( lm( log(vr) ~ log(mn) ) )

(Intercept) log(mn)

1.399527 1.553380

> # Group by Decade

> Decade <- cut( quilpie$Year, breaks=seq(1920, 1990, by=10) )

> mn <- tapply( quilpie$Rain, Decade, "mean")

> vr <- tapply( quilpie$Rain, Decade, "var")

> coef( lm( log(vr) ~ log(mn) ) )

466 12 Tweedie GLMs

(Intercept) log(mn)

0.2821267 1.9459524

The two methods produce diﬀerent estimates of ξ, but both satisfy 1 ≤ ξ ≤ 2.



A more rigorous method for estimating ξ, that uses the information in the

explanatory variables and is not dependent on the arbitrary dividing of the

data, is to compute the maximum likelihood estimator of ξ. A convenient way

to organize the calculations is via the proﬁle likelihood for ξ. Various values

of ξ are chosen, then the Tweedie glm is ﬁtted for each value of ξ assuming

that ξ is ﬁxed, and the log-likelihood computed at each value of ξ. This

gives the proﬁle log-likelihood. The value of ξ giving the largest proﬁle log-

likelihood is the proﬁle likelihood estimate. A plot of the proﬁle log-likelihood

against various values of ξ is often useful.

One diﬃculty with this method is that the likelihood function for the

Tweedie edms must be computed, but the probability function for Tweedie

edms does not have a closed form (Sect. 12.2.2) except in the well-known

special cases. However, numerical methods exist for accurately evaluating the

Tweedie densities [15, 16], and are used in the r function tweedie.profile()

(in package tweedie [13]) for computing the proﬁle likelihood estimate of ξ.

The use of tweedie.profile() is demonstrated in Example 12.4, and brieﬂy

in Example 12.5. Sometimes, estimating ξ using tweedie.profile() may be

slow, but once the estimate of ξ has been determined ﬁtting the Tweedie glm

using glm() is fast (as computing the value of the likelihood is not needed

for estimation).

Example 12.4. The total monthly July rainfall at Quilpie, considered in Ex-

ample 12.2 (data set: quilpie), is continuous but has exact zeros. Following

the conclusion in Sect. 4.12 (p. 202), we consider modelling the total July

rainfall as a function of the soi phase [35]. The

soi phase is clearly of some

importance (Fig. 12.4,leftpanel):

> quilpie$Phase <- factor(quilpie$Phase) # Declare Phase as a factor

> plot( Rain ~ Phase, data=quilpie, ylab="Total July rainfall",

ylim=c(0, 100), las=1)

Also observe that the variation is greater for larger average rainfall amounts.

A suitable estimate of ξ can be found using tweedie.profile():

> library(tweedie)

> out <- tweedie.profile( Rain ~ Phase, do.plot=TRUE, data=quilpie)

The proﬁle likelihood plot (Fig. 12.4, right panel) shows the likelihood is

computed at a small number of ξ values as ﬁlled circles, then a smooth curve

is drawn through these points. The horizontal dashed line is the value of

the log-likelihood at which the approximate 95% conﬁdence interval for ξ is

located, using that, approximately,

12.3 Tweedie GLMs 467

12345

100

Phase

Total July rainfall

1.2 1.3 1.4 1.5 1.6 1.7 1.8

−245

−240

−235

−230

−225

ξ index

(95% confidence interval)

Fig. 12.4 The total July rainfall at Quilpie plotted against soi phase (left panel), and

the proﬁle likelihood plot for estimating ξ (right panel) (Example 12.4)

(

ξ; y;

φ, ˆμ) − (ξ; y;

, ˆμ

)

∼ χ

where (ξ; y;

, ˆμ

) is the proﬁle log-likelihood at ξ and (

ξ; y;

φ, ˆμ)isthe

overall maximum.

The output object, named out in the above, contains a lot of information

(see names(out)), including the estimate of ξ (as xi.max), the nominal 95%

conﬁdence interval for ξ (as ci), and the mle of φ (as phi.max):

> # The index parameter, xi

> xi.est <- out$xi.max

> c( "MLE of xi" = xi.est, "CI for xi" = out$ci )

MLE of xi CI for xi1 CI for xi2

1.371429 1.270144 1.499132

> # Phi

> c("MLE of phi"=out$phi.max)

MLE of phi

5.558709



A technical diﬃculty sometimes arises in estimating ξ, which has been

observed by many authors [20, 23, 26]. Recall (Sect. 12.2) that the Tweedie

distribution with ξ = 1 is suitable for modelling discrete data where y =

0,φ,2φ, 3φ,.... If the responses y are rounded to, say, one decimal place, then

the log-likelihood may be maximized by setting φ =0.1andξ = 1. Likewise,

if the data are rounded to zero decimal places, then the log-likelihood may

be maximized setting φ =1andξ = 1 (Example 12.5). Dunn and Smyth [15]

discuss this problem in greater detail. In practice, the proﬁle likelihood plot

produced by tweedie.profile() should be examined, and values of ξ near

1 should be avoided as necessary.

Example 12.5. Consider 100 observations randomly generated from a Tweedie

distribution with ξ =1.5, μ =2andφ =0.5.

468 12 Tweedie GLMs

> mu <- 2; phi <- 0.5; xi <- 1.5; n <- 100

> library(tweedie)

> rndm <- rtweedie(n, xi=xi, mu=mu, phi=phi)

We then estimate the value of ξ from the original data, and then after round-

ing to one and to zero decimal places (Fig. 12.5):

> xi.vec <- seq(1.01, 1.75, by=0.05)

> out.est <- tweedie.profile( rndm ~ 1, xi.vec=xi.vec)

> out.1 <- tweedie.profile( round(rndm, 1) ~ 1, xi.vec=xi.vec)

> out.0 <- tweedie.profile( round(rndm, 0) ~ 1, xi.vec=xi.vec)

Now compare the estimates of ξ and φ for the three cases:

> xi.max <- out.est$xi.max

> xi.1 <- out.1$xi.max

> xi.0 <- out.0$xi.max

> compare <- array( dim=c(2, 4))

> colnames(compare) <- c("True", "Estimate", "One d.p.", "Zero d.p.")

> rownames(compare) <- c("xi", "phi")

> compare[1,] <- c(xi, xi.max, xi.1, xi.0)

> compare[2,] <- c(phi, out.est$phi.max, out.1$phi.max, out.0$phi.max)

> round(compare, 3)

True Estimate One d.p. Zero d.p.

xi 1.5 1.696 1.710 1.010

phi 0.5 0.411 0.407 1.003

For these data, rounding to one decimal place only makes a small diﬀerence

to the log-likelihood, and to the estimate of ξ. However, rounding to zero

decimal places produces an artiﬁcial maximum in the log-likelihood, where

ξ → 1andφ → 1. 

1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7

−200

−150

−100

−50

Log−likelihood

Original data

Rounded to one decimal place

Rounded to zero decimal places

Fig. 12.5 Estimating ξ for some randomly generated data from a Tweedie distribution

with ξ =1.5. The gray vertical line is the true value of ξ (Example 12.5)

12.3 Tweedie GLMs 469

12.3.3 Fitting Tweedie GLMs

Once an estimate of ξ has been obtained, the Tweedie glm can be ﬁtted

in r using the usual glm() function. The Tweedie distributions are denoted

in r using family=tweedie() in the glm() call, after loading the statmod

package. The call to family=tweedie() must specify which Tweedie edm is

to be used (that is, the value of ξ), using the input var.power; for example,

family=tweedie(var.power=3) indicates the Tweedie edm with V (μ)=μ

should be used. The link function is speciﬁed using the input link.power,

where η = μ

link.power

. Usually, link.power=0 which corresponds to the loga-

rithmic link function. The logarithm link function is the most commonly-used

link function with Tweedie glms. As usual, the default link function is the

canonical link function.

Once the model has been ﬁtted, quantile residuals [14] are recommended

for diagnostic analysis, especially when 1 <ξ<2 when exact zeros may be

present. Using more than one set of quantile residuals is recommended, due

to the randomization used at y = 0 (Sect. 8.3.4.2).

Example 12.6. For the Quilpie rainfall data (data set: quilpie), the estimate

of ξ found in Example 12.4 is ξ ≈ 1.37. To ﬁt this model in r:

> xi.est <- round(xi.est, 2); xi.est

[1] 1.37

> m.quilpie <- glm( Rain ~ Phase, data=quilpie,

family=tweedie(var.power=xi.est, link.power=0) )

> printCoefmat(coef(summary(m.quilpie)))

Estimate Std. Error t value Pr(>|t|)

(Intercept) -2.1691 1.9560 -1.1089 0.271682

Phase2 5.6923 1.9678 2.8927 0.005239 **

Phase3 3.5153 2.0600 1.7064 0.092854 .

Phase4 5.0269 1.9729 2.5480 0.013287 *

Phase5 4.6468 1.9734 2.3547 0.021665 *

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

We can compare the Pearson, deviance and quantile residuals (Fig. 12.6):

> dres <- resid(m.quilpie) # The default residual

> pres <- resid(m.quilpie, type="pearson")

> qres1 <- qresid(m.quilpie) # Quantile resids, replication 1

> qres2 <- qresid(m.quilpie) # Quantile resids, replication 2

> qqnorm(dres, main="Deviance residuals", las=1); qqline(dres)

> qqnorm(pres, main="Pearson residuals", las=1); qqline(pres)

> qqnorm(qres1, main="Quantile residuals (set 1)", las=1); qqline(qres1)

> qqnorm(qres2, main="Quantile residuals (set 2)", las=1); qqline(qres2)

Compare the Q–Q plot of the deviance, Pearson and quantile residuals

(Fig. 12.6): the exact zeros appear as bands in the bottom left corner when

using the deviance residuals. When the data contain a large number of exact

zeros, this feature makes the plots of the deviance residuals hard to read.

470 12 Tweedie GLMs

−2 −1 0 1 2

−4

−2

Deviance residuals

Theoretical Quantiles

Sample Quantiles

−2 −1 0 1 2

−2

Pearson residuals

Theoretical Quantiles

Sample Quantiles

−2 −1 0 1 2

−2

−1

Quantile residuals (set 1)

Theoretical Quantiles

Sample Quantiles

−2 −1 0 1 2

−2

−1

Quantile residuals (set 2)

Theoretical Quantiles

Sample Quantiles

Fig. 12.6 Q–Q plots for the Pearson, deviance and quantile residuals for the Tweedie

glm ﬁtted to the Quilpie rainfall data. Two realization of the quantile residuals are

shown (Example 12.6)

The quantile residuals use a small amount of randomization (Sect. 8.3.4.2)to

remove these bands. The Q–Q plot of the quantile residuals for these data

suggest the model is adequate. Q–Q plots of the other residuals make it

diﬃcult to draw deﬁnitive conclusions. For this reason, the use of quantile

residuals is strongly recommended for use with Tweedie glms with 1 <ξ<2.

Other model diagnostics (Fig. 12.7) also suggest the model is reasonable:

> plot( qres1 ~ fitted(m.quilpie), las=1,

xlab="Fitted values", ylab="Quantile residuals" )

> plot( cooks.distance(m.quilpie), type="h", las=1,

ylab="Cook's distance, D")

> plot( qresid(m.quilpie) ~ factor(quilpie$Phase), las=1,

xlab="Phase", ylab="Quantile residuals" )

12.3 Tweedie GLMs 471

0 5 10 15 20 25 30 35

−2

−1

Fitted values

Quantile residuals

0 10203040506070

0.0

0.1

0.2

0.3

0.4

Index

Cook's distance, D

12345

−2

−1

Phase

Quantile residuals

0.0 0.2 0.4 0.6 0.8

0.0

0.2

0.4

0.6

0.8

1.0

Proportion of zeros in data

Expected prob. of zero rainfall

Phase 1

Phase 2

Phase 3

Phase 4

Phase 5

Fig. 12.7 The diagnostics for the Tweedie glm ﬁtted to the Quilpie rainfall data (Ex-

amples 12.6 and 12.7)

No observations are identiﬁed as inﬂuential using Cook’s distance, though

dffits identiﬁes one observation as inﬂuential and cv identiﬁes eight:

> q.inf <- influence.measures(m.quilpie)

> colSums(q.inf$is.inf)

dfb.1_ dfb.Phs2 dfb.Phs3 dfb.Phs4 dfb.Phs5 dffit cov.r cook.d

00000180

hat



As shown in Sect. 12.2.4, Tweedie glms with 1 <ξ<2 can be developed

as a Poisson sum of gamma distributions. A ﬁtted glm can be interpreted

on this basis too.

Example 12.7. For the Quilpie rainfall data (data set: quilpie), the predicted

number of zero-rainfall months ˆπ

for each soi phase can be compared to the

actual proportion of months in the data with zero rainfall for each soi phase.

To ﬁnd the mle of π

using (12.5), the mle of φ must be used, which was

conveniently returned by tweedie.profile() as phi.max (Example 12.4).

The plot of the expected probability of a zero against the proportion of zeros

in the data for each soi phase is shown in Fig. 12.7 (bottom right panel):

472 12 Tweedie GLMs

> # Modelled probability of P(Y=0)

> new.phase <- factor( c(1, 2, 3, 4, 5) )

> mu.phase <- predict(m.quilpie, newdata=data.frame(Phase=new.phase),

type="response")

> names(mu.phase) <- paste("Phase", 1:5)

> mu.phase

Phase 1 Phase 2 Phase 3 Phase 4 Phase 5

0.1142857 33.8937500 3.8428573 17.4235294 11.9142857

> phi.mle <- out$phi.max

> pi0 <- exp( -mu.phase^(2 - xi.est) / (phi.mle * (2 - xi.est) ) )

> # Observed probability of P(Y=0)

> prop0 <- tapply(quilpie$Rain, quilpie$Phase,

function(x){sum(x==0)/length(x)})

> plot( pi0 ~ prop0, xlab="Proportion of zeros in data", ylim=c(0, 1),

ylab="Expected prob. of zero rainfall", las=1 )

> abline(0, 1, lwd=2) # The line of equality

> text(prop0, pi0, # Adds labels to the points

labels=paste("Phase", levels(quilpie$Phase)),

pos=c(2, 4, 1, 4, 3)) # These position the labels; see ?text

The proportion of months with zero rainfall are predicted with reasonable

accuracy. The Tweedie glm seems a useful model for the total July rainfall

in Quilpie.

As suggested in Sect. 12.2.4 (p. 463), the estimated parameters of the glm

can be used to interpret the underlying Poisson and gamma distributions. To

do so, use the tweedie.convert() function in package tweedie:

> out <- tweedie.convert(xi=xi.est, mu=mu.phase, phi=phi.mle)

> downscale <- rbind("Poisson mean" = out$poisson.lambda,

"Gamma mean" = out$gamma.mean,

"Gamma dispersion" = out$gamma.phi)

> colnames(downscale) <- paste("Phase", 1:5)

> downscale

Phase 1 Phase 2 Phase 3 Phase 4 Phase 5

Poisson mean 0.07281493 2.628215 0.6668339 1.728229 1.3602174

Gamma mean 0.16582834 1.362530 0.6088689 1.065178 0.9254371

Gamma dispersion 1.44678583 97.673944 19.5044793 59.694036 45.0588947

In the context of rainfall modelling, this interpretation in terms of λ

∗

, μ

∗

and φ

∗

is a form of statistical downscaling [11]. The estimates of the Poisson

mean λ

∗

show the mean number of rainfall events in July when the soi

is in each phase, and the estimates of the gamma mean μ

∗

give the mean

amount of rainfall in each rainfall event for each soi phase. For Phase 2 the

model predicts a mean of 2.628 rainfall events occur in July, with a mean of

1.363 mm in each. The mean monthly July rainfall predicted by the model

agrees with the observed mean rainfall in the data:

> tapply( quilpie$Rain, quilpie$Phase, "mean") # Mean rainfall from data

12345

0.1142857 33.8937500 3.8428571 17.4235294 11.9142857

12.4 Case Studies 473

> mu.phase # Mean rainfall from model

Phase 1 Phase 2 Phase 3 Phase 4 Phase 5

0.1142857 33.8937500 3.8428573 17.4235294 11.9142857

(Note that the boxplots in Fig. 12.4 show the median rainfall, not the mean.)

The estimates of μ

∗

and φ

∗

are the mean and dispersion parameters for the

gamma distribution ﬁtted to the total July rainfall amount for each soi phase.

Notice that 1 <ξ<2 since exact zeros are present in the data. However,

exact zeros are not present in every soi Phase:

> tapply(quilpie$Rain, quilpie$Phase, "min")

12345

0.0 3.6 0.0 0.0 0.0

In other words, even though no months with exactly zero rainfall were ob-

served during Phase 2, the Tweedie glm assigns a (small) probability that

such an event could occur:

> round(out$p0, 2)

[1] 0.93 0.07 0.51 0.18 0.26



12.4 Case Studies

12.4.1 Case Study 1

A study of performance degradation of electrical insulation from accelerated

tests [28, 29, 32] measured the dialetric breakdown strength (in kilovolts) for

eight time periods (in weeks) and four temperatures (in degrees Celsius). Four

measurements are given for each time–temperature combination (data set:

breakdown), and the study can be considered as a 8 ×4 factorial experiment.

> data(breakdown)

> breakdown$Time <- factor(breakdown$Time)

> breakdown$Temperature <- factor(breakdown$Temperature)

> summary(breakdown)

Strength Time Temperature

Min. : 1.00 1 :16 180:32

1st Qu.:10.00 2 :16 225:32

Median :12.00 4 :16 250:32

Mean :11.24 8 :16 275:32

3rd Qu.:13.53 16 :16

Max. :18.50 32 :16

(Other):32

474 12 Tweedie GLMs

Time

Mean strength (kV)

1 2 4 8 16 32 48 64

Temperature

180

225

250

275

Fig. 12.8 A plot of the dialetric breakdown data (Sect. 12.4.1)

A plot of the data (Fig. 12.8) may suggest that a temperature of 275

◦

Cis

diﬀerent than the rest:

> bd.means <- with(breakdown,

tapply(Strength, list(Time, Temperature), "mean"))

> matplot( bd.means, type="b", col="black",

pch=1:4, lty=1:4, las=1, ylim=c(0, 20),

xlab="Time", ylab="Mean strength (kV)", axes=FALSE)

> axis(side=1, at=1:8, labels=levels(breakdown$Time))

> axis(side=2, las=2); box()

> legend("bottomleft", pch=1:4, lty=1:4, merge=FALSE,

legend=levels(breakdown$Temperature), title="Temperature" )

The plot also seems to show that the variance increases as Time increases.

To consider ﬁtting a Tweedie glm to the data, we use tweedie.profile()

to ﬁnd an estimate of ξ:

> bd.xi <- tweedie.profile(Strength~Time*Temperature, data=breakdown,

do.plot=TRUE, xi.vec=seq(1.2, 2, length=11))

> bd.m <- glm( Strength~factor(Time) * factor(Temperature), data=breakdown,

family=tweedie(link.power=0, var.power=bd.xi$xi.max))

> anova(bd.m, test="F")

Notice that 1 <ξ<2 even though all breakdown strengths are positive:

> bd.xi$xi.max

[1] 1.591837

The Q–Q plot (Fig. 12.9, right panel) suggests no major problems with the

model:

> qqnorm( resid(bd.m), las=1 ); qqline( resid(bd.m) )

12.4 Case Studies 475

1.2 1.4 1.6 1.8 2.0

−154.5

−154.0

−153.5

−153.0

−152.5

−152.0

−151.5

−151.0

ξ index

(95% confidence interval)

−2 −1 0 1 2

−0.3

−0.2

−0.1

0.0

0.1

0.2

0.3

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

Fig. 12.9 The proﬁle-likelihood plot (left panel) and Q–Q plot of quantile residuals

(right panel) for the dialetric breakdown data (Sect. 12.4.1)

1.5 2.0 2.5 3.0 3.5 4.0 4.5

ξ index

(95% confidence interval)

Fig. 12.10 The proﬁle likelihood plot for estimating the value of the Tweedie index

parameter ξ for the poison data (Sect. 12.4.2)

12.4.2 Case Study 2

Consider the survival times data ﬁrst introduced in Example 12.1, where

a Tweedie edm with ξ ≈ 4 was suggested for modelling the data (data

set: poison). To ﬁnd the appropriate Tweedie edm for modelling the data

more formally, initially determine an estimate of ξ using the proﬁle likeli-

hood (Fig. 12.10), using the r function tweedie.profile() from the package

tweedie:

> data(poison)

> library(tweedie) # To provide tweedie.profile()

476 12 Tweedie GLMs

> pn.profile <- tweedie.profile( Time ~ Trmt * Psn, data=poison,

do.plot=TRUE)

.......Done.

> c("xi: MLE"=pn.profile$xi.max, "xi: CI"=pn.profile$ci)

xi: MLE xi: CI1 xi: CI2

3.826531 2.866799 NA

These results suggest that ﬁtting a Tweedie glm using

ξ = 4 is not unrea-

sonable:

> library(statmod) # To provide the tweedie() family

> poison.m1 <- glm( Time ~ Trmt * Psn, data=poison,

family=tweedie(link.power=0, var.power=4))

> anova( poison.m1, test="F")

Df Deviance Resid. Df Resid. Dev F Pr(>F)

NULL 47 62.239

Trmt 3 19.620 44 42.619 32.7270 2.189e-10 ***

Psn 2 32.221 42 10.398 80.6195 5.053e-14 ***

Trmt:Psn 6 2.198 36 8.199 1.8334 0.12

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

The interaction is not signiﬁcant. The ﬁtted model without the interaction

term is:

> poison.m2 <- update( poison.m1, . ~ Trmt + Psn )

> summary(poison.m2)

Call:

glm(formula = Time ~ Trmt + Psn, family = tweedie(link.power = 0,

var.power = 4), data = poison)

Deviance Residuals:

Min 1Q Median 3Q Max

-1.29925 -0.32135 -0.03321 0.20951 0.94121

Coefficients:

Estimate Std. Error t value Pr(>|t|)

(Intercept) -0.82828 0.07938 -10.435 3.10e-13 ***

TrmtB 0.61792 0.08812 7.012 1.40e-08 ***

TrmtC 0.15104 0.06414 2.355 0.0233 *

TrmtD 0.49832 0.08053 6.188 2.13e-07 ***

PsnII -0.22622 0.09295 -2.434 0.0193 *

PsnIII -0.77091 0.08007 -9.628 3.43e-12 ***

---

Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1''1

(Dispersion parameter for Tweedie family taken to be 0.2656028)

Null deviance: 62.239 on 47 degrees of freedom

Residual deviance: 10.398 on 42 degrees of freedom

AIC: NA

Number of Fisher Scoring iterations: 8

12.4 Case Studies 477

IIIIII

−2

−1

Poison

Quantile residuals

ABCD

−2

−1

Time

Quantile residuals

0.2 0.4 0.6 0.8

−2

−1

Fitted values

Quantile residuals

0 10203040

0.00

0.02

0.04

0.06

0.08

0.10

0.12

Index

Cook's distance, D

−2 −1 0 1 2

−2

−1

Normal Q−Q Plot

Theoretical Quantiles

Sample Quantiles

Fig. 12.11 The diagnostics for the ﬁnal model poison.m2 ﬁtted to the poison data

(Sect. 12.4.2)

Notice the aic is not computed by default, because the necessary numerical

computations may be time consuming. However, the aic can be computed

explicitly using the function AICtweedie() in package tweedie, suggesting

the non-interaction model is preferred:

> c("With int" = AICtweedie(poison.m1),

"Without int." = AICtweedie(poison.m2))

With int Without int.

-87.57423 -88.32050

The diagnostic plots suggest model poison.m2 is adequate (Fig. 12.11),

though the residuals for Poison 2 are more variable than for other poisons:

> plot( qresid(poison.m2) ~ poison$Psn, las=1,

xlab="Poison", ylab="Quantile residuals" )

> plot( qresid(poison.m2) ~ poison$Trmt, las=1,

xlab="Time", ylab="Quantile residuals" )

> plot( qresid(poison.m2) ~ fitted(poison.m2), las=1,

xlab="Fitted values", ylab="Quantile residuals" )

> plot( cooks.distance(poison.m2), type="h", las=1,

ylab="Cook's distance, D")

> qqnorm( qr<-qresid(poison.m2), las=1 ); qqline(qr)

The ﬁnal model is glm(Tweedie, ξ = 4; log):



y ∼ Tw

ξ=4

(ˆμ,

φ =0.2656) (random)

log E[y] = log ˆμ =

(systematic)

478 12 Tweedie GLMs

where the x

represent dummy variables for the treatment type (j =1, 2, 3)

and poison type (j =4, 5). Observe the Pearson estimate of φ is given in the

output of summary(poisson.m2) as

φ =0.2656.

These data have also been analysed [6] using the Box–Cox transformation

λ = −1, corresponding to y

∗

=1/y. This transformation is the variance-

stabilizing transformation approximating the Tweedie glm with ξ = 4 (Ta-

ble 5.2).

12.5 Using R to Fit Tweedie GLMs

Fitting Tweedie glms require extra r libraries to be installed (Sect. A.2.5):

•Thetweedie package [13] is useful for estimating the appropriate value

of ξ for a given data set using the function tweedie.profile().

•Thestatmod package [33] is essential for ﬁtting Tweedie glms, provid-

ing the tweedie() glm family function. It also provides the function

qresid() for computing quantile residuals, whose use is strongly recom-

mended with Tweedie glms.

The tweedie.profile() function ﬁxes the value of ξ and ﬁts the Tweedie

glm, then computes the log-likelihood. After doing so for various values of

ξ, the proﬁle likelihood estimate of ξ is the value producing the largest value

of the log-likelihood. The function may be slow for very large data sets.

The use of tweedie.profile() requires a formula for specifying the sys-

tematic component in the same form as used for glm(). Other important

inputs are:

• xi.vec: The vector of ξ-values to consider. By default, if the response con-

tains zeros then xi.vec = seq(1.2, 1.8, by=0.1), and if the response

does not contain zeros then xi.vec = seq(1.5, 5, by=0.5). The likeli-

hood function is smoothed by default (unless do.smooth=FALSE) through

the likelihood values computed at these values of ξ given in xi.vec.

• do.plot: Indicates whether to produce a plot of the log-likelihood against

ξ, called a proﬁle likelihood plot. Producing the plot is recommended

to ensure the function has worked correctly and to ensure the problem

identiﬁed in Sect. 12.3.2 has not occurred. If the plot is not smooth, the

method may need to be changed. The log-likelihood is evaluated numer-

ically at the values of ξ in xi.vec, and these evaluations shown with

a ﬁlled circle in the proﬁle likelihood plot if do.plot=TRUE (by default,

do.plot=FALSE). An interpolation spline is drawn if do.smooth=TRUE

(the default).

• method: The method used for numerically computing the log-likelihood.

Occasionally the method needs to be changed explicitly to avoid diﬃcul-

ties (errors messages may appear; the log-likelihood may be computed as

±∞ (shown as Inf or -Inf in r); or the plot of the log-likelihood against

12.6 Summary 479

ξ is not smooth). The options include method = "series", method =

"inversion",ormethod = "interpolation". The series method [15]

often works well when the inversion method fails [16]. The interpolation

method uses either the series or an interpolation of the inversion method

results, so is often faster but may produce discontinuities in the proﬁle

likelihood plot when the computations change regimes.

• do.ci: Produces a nominal 95% conﬁdence interval for the mle of ξ when

do.ci=TRUE (which is the default).

The function tweedie.profile() returns numerous quantities, the most use-

ful of which are:

• xi.max: The proﬁle likelihood estimate of ξ.

• phi.max:Themle of φ.

• ci: The limits of the approximate 95% conﬁdence interval for ξ (returned

if do.ci=TRUE, which is the default).

See ?tweedie.profile for further information.

After installing the statmod package, specify a Tweedie glm in r us-

ing glm(formula, family=tweedie(var.power, link.power)), where the

value of ξ is var.power,andlink.power speciﬁes the link function in the

form μ

link.power

= η. Most commonly, link.power is zero, specifying the

logarithmic link function. (The default link function is the canonical link

function; Problem 12.5.) The aic is not computed and shown in the model

summary(), because the computations may be slow. If necessary, the aic can

be computed directly using AICtweedie() in package tweedie.

12.6 Summary

Chapter 12 focuses on ﬁtting Tweedie glms to two types of data: Tweedie

glms for positive continuous data, and Tweedie glms for positive continuous

data with exact zeros.

The Tweedie distributions are edms with the variance function V (μ)=μ

for ξ/∈ (0, 1) (Sect. 12.2). Special cases of Tweedie distributions previously

studied are the normal (ξ = 0), Poisson (ξ =1andφ = 1), gamma (ξ =2)

and inverse Gaussian (ξ = 3) distributions (Sect. 12.2).

The unit deviance is given in (12.2). The residual deviance D(y, ˆμ)is

suitably described by a χ

n−p



distribution if φ ≤ y

2−ξ

/3, but is exact when

ξ = 3 (the inverse Gaussian distribution) (Sect. 12.2.2).

For ξ ≥ 2, the Tweedie distributions, and hence Tweedie glms, are appro-

priate for positive continuous data. For 1 <ξ<2, the Tweedie distributions,

and hence Tweedie glms, are appropriate for positive continuous data with

exact zeros (Sect. 12.2).

The value of ξ is estimated using the tweedie.profile() function from

the r package tweedie (Sect. 12.3).

480 12 Tweedie GLMs

Problems

Selected solutions begin on p. 547.

12.1. Deduce the expressions for θ and κ(θ) for the Tweedie edms, as given

in (12.1)(p.460), using that V (μ)=μ

. Set the arbitrary constants of

integration to zero. (Hint: Follow the approach in Sect. 5.3.6,p.217.)

12.2. In Problem 12.1, expressions for θ and κ(θ) were found by setting the

arbitrary constants of integration to zero. In this problem we consider an

alternative parameterization [15].

1. By appropriately choosing the constants of integration, show that alter-

native expressions for θ and κ(θ) can be written as

θ =

⎧

⎪

⎨

⎪

⎩

1−ξ

− 1

1 − ξ

for ξ =1

log μ for ξ =1

and κ(θ)=

⎧

⎪

⎨

⎪

⎩

2−ξ

− 1

2 − ξ

for ξ =2

log μ for ξ =2

(12.6)

2. Show that θ is continuous in ξ.(Hint: Use that lim

α→0

− 1)/α →

log x.)

3. Likewise, show that κ(θ) is continuous in ξ.

12.3. Deduce the unit deviance for the Tweedie edms given in (12.2)(p.460).

12.4. Using the guideline presented in Sect. 5.4.5 (p. 226), show that the

residual deviance D(y, ˆμ) is likely to follow a χ

n−p



distribution when φ ≤

2−ξ

/3 when ξ ≥ 1. Hence show that the saddlepoint approximation is likely

to be poor for continuous data with exact zeros.

12.5. Deduce the canonical link function for the Tweedie edms.

12.6. Consider the rescaling identity in (12.3).

1. Using this identity, deduce the Tweedie edm for which the value of φ

does not change when a change of measurement units (say, from grams

to kilograms) is applied to the data y.

2. Using this identity, deduce the Tweedie edm for which value of φ increases

by the same factor as that used for a change of measurement units in the

data y.

3. What does the identity reveal about the case of the inverse Gaussian

distribution in the case of a change in measurement units in y?

4. Show that the probability function for any Tweedie edm P

(y; μ, φ)can

be computed by an evaluation at μ = 1 (that is, P

∗

;1,φ

∗

)), by ﬁnding

the appropriately-redeﬁned values of y

∗

and φ

∗

12.7. Consider the Box–Cox transformation (Sect. 3.9,p.116).

12.6 Summary 481

1. Show that the Box–Cox transformation for any λ approximates ﬁtting a

glm basedonaedm with variance function V (μ)=μ

2(1−λ)

if μ>0.

(Use a Taylor series of the transformation expanded about the mean μ,

as in Sect. 5.8.)

2. No Tweedie edms exist when 0 <ξ<1. Use this result to show no

equivalent power-variance glm exists for the Box–Cox transformations

corresponding to 0.5 <λ<1.

12.8. A study of monthly rainfall in Australia [22] ﬁtted Tweedie glmstoa

number of diﬀerent rainfall stations using

ξ =1.6. For Bidyadanga monthly

rainfall from 1912 to 2007, the ﬁtted systematic component was

log ˆμ

=2.903 + 1.908 sin(2πm/12) + 0.724 cos(2πm/12),

where m =1, 2,...12 corresponds to the month of the year (for example,

February corresponds to m = 2). The standard errors for the parameter

estimates are (respectively) 0.066, 0.090 and 0.085, and the mle of φ is 8.33.

1. Compute the Wald statistic for testing if each regression parameter is

zero.

2. Plot the value of ˆμ

against m for m =1,...,12 for Bidyadanga.

3. Plot the predicted value of π

against m for m =1,...,12 for Bidyadanga.

12.9. A study [10] of the walking habits of adults living in south-east

Queensland, Australia, compared diﬀerent types of Statistical Areas classi-

ﬁed by their walk score [9] as ‘Highly walkable’, ‘Somewhat walkable’, ‘Car-

dependent’ or ‘Very car-dependent’ (Table 12.3). The Tweedie glm was ﬁtted

using

ξ =1.5.

1. Explain the diﬀerences between the predicted mean walking times in

both sections of the table. Why are the predicted means all larger for the

second model (‘walking adults’)?

2. A Tweedie glm was ﬁtted for ‘All adults’ and a gamma glm for ‘Walking

adults’. Explain why these models may have been chosen.

3. The deviance from the ﬁtted Tweedie glm was 5976.08 on 1242 degrees

of freedom. Use this information to ﬁnd an estimate of φ.

4. Using the Tweedie glm, ﬁnd an estimate of the proportion of all adults

who did no walking in each of the four types of walkability descriptions,

and comment. Why are these values not the mlesoftheπ

12.10. A study of polythene use by cosmetic companies in the uk [19]

hypothesized a relationship with company turnover (Table 12.4; data set:

polythene). Consider two Tweedie glms models for the data, both using

a logarithmic link function for the systematic component: the ﬁrst using

Polythene~Turnover, and the second using Polythene~log(Turnover).

1. Find estimates of ξ for each model.

482 12 Tweedie GLMs

Table 12.3 Predicted mean number of minutes of walking per day in four types of

regions, adjusted for work status, household car ownership and driver’s license status

(Problem 12.9)

All adults Walking adults

Predicted Predicted

n mean n mean

Highly walkable 214 7.5 155 25.5

Somewhat walkable 407 4.7 255 25.4

Car-dependent 441 2.9 254 21.2

Very car-dependent 187 2.5 90 18.3

Table 12.4 The company turnover and polythene use for 23 cosmetic companies in the

uk (to preserve conﬁdentiality, the data were scaled) (Problem 12.10)

Polythene use Turnover Polythene use Turnover Polythene use Turnover

(in tonnes) (in £00 000) (in tonnes) (in £00 000) (in tonnes) (in £00 000)

0.04 0.02 31.50 9.85 587.83 83.94

1.60 0.23 472.50 21.13 1068.92 106.13

0.00 3.17 0.00 24.40 676.20 156.01

0.00 3.46 94.50 30.18 1056.30 206.43

3.78 3.55 55.94 40.13 1503.60 240.51

29.40 4.62 266.53 68.40 1438.50 240.93

8.00 5.71 252.53 70.88 2547.30 371.68

95.13 7.77 4298.70 391.33

2. Fit the glms to the data, and interpret the models.

3. On two separate plots of polythene use against turnover, plot the system-

atic components of both models, including the 95% conﬁdence interval

for the ﬁtted lines. Comment on the models.

4. Compute the aic for both models, and comment.

5. Produce the appropriate diagnostic plots for both models.

6. Deduce a suitable model for the data.

12.11. Consider the permeability of building material data given in Ta-

ble 11.2 (data set: perm). In Sect. 11.7 (p. 440), the positive continuous re-

sponse was modelled using an inverse Gaussian glm for interpretation rea-

sons. Jørgensen [24] also considers a gamma (ξ =2)glm for the data.

1. Determine an estimate of ξ using tweedie.profile(). What edm is

suggested?

2. Fit a suitable Tweedie glm ensuring an appropriate diagnostic analysis.

12.12. A study of human energy expenditure measured the energy expendi-

ture y of 104 females over a 24-h period (Table 12.5; data set: energy), and

also recorded their fat-tissue mass x

and non-fat tissue x

mass [18, 24].

A model for the energy expenditure is E[y]=β

+ β

, assuming the

12.6 Summary 483

Table 12.5 The energy expenditure and mass of 104 females (units not given). Only

the ﬁrst six observations are shown (Problem 12.12)

Energy expenditure Mass of fat tissue Mass of non-fat tissue

60.08 17.31 43.22

60.08 34.09 43.74

63.69 33.03 48.72

64.36 9.14 50.96

65.37 30.73 48.67

66.05 20.74 65.31

energy expenditure for each tissue type is homogenous. Since the total mass

is M = x

+ x

, divide by M and rewrite as E[¯y]=β

+(β

− β

)¯x, where

¯y = y/M is the energy expenditure per unit mass, and ¯x = x

/M is the

proportion of fat-tissue mass.

1. Plot ¯y against ¯x and conﬁrm the approximate linear relationship between

the variables.

2. Use tweedie.profile() to estimate ξ for the data. Which Tweedie edms

is appropriate?

3. Find a suitable glm for the data, ensuring a diagnostic analysis.

12.13. The data described in Table 12.6 (data set: motorins1) concern third

party motor insurance claims in Sweden for the year 1977 [1, 21, 32]. The

description of the data states that Swedish motor insurance companies “ap-

ply identical risk arguments to classify customers, and thus their portfolios

and their claims statistics can be combined” [1, p. 413]. The data set con-

tains 315 observations representing one of the zones in the country (covering

Stockholm, Göteborg, and Malmö with surroundings).

For the remainder of the analysis, consider payments in millions of Kroner.

Policies are categorized by kilometres of travel (ﬁve categories), the no-claim

bonus (seven categories) and make of car (nine categories), for a total of 315

categories. Of these, 20 contain exactly zero claims, so the total payout in

those categories is exactly zero; in other categories, the total payout can be

consider continuous. Find an appropriate model for the data. (Hint:You

will need to change the range of ξ values considered by tweedie.profile()

using the xi.vec input.)

Using your ﬁtted model, interpret the model using the parameters of the

underlying Poisson and gamma distributions. (Hint: See (12.4), p. 464.)

12.14. The total monthly August rainfall for Emerald (located in Queens-

land, north eastern Australia) from 1889 to 2002 is shown in Table 12.7 (data

set: emeraldaug) with the monthly average southern oscillation index (soi).

Negative values of the soi often indicate El Niño episodes, which are often

associated with reduced rainfall in eastern and northern Australia [27].

484 12 Tweedie GLMs

Table 12.6 A description of the variables used in the Swedish insurance claims data

set (Problem 12.13)

Variable Description

Kilometres: Kilometres travelled per year:

1: Less than 1000

2: 1000–15,000

3: 15,000–20,000

4: 20,000–25,000

5: More than 25,000

Bonus: No claims bonus; the number of years since last claim, plus one

Make: 1–8 represent eight diﬀerent common car models. All other models are

combined in class 9

Insured: Number of insured in policy-years

Claims: Number of claims

Payment: Total value of payments in Skr (Swedish Kroner)

Table 12.7 The total monthly rainfall in August from 1889–2002 in Emerald, Australia,

plus the monthly average soi and corresponding soi phases. The ﬁrst ﬁve observations

are shown (Problem 12.14)

Year Rain (in mm) soi soi phase

1889 15.4 2.15

1890 47.5 −3.15

1891 45.7 −8.95

1892 0.0 5.92

1893 108.7 7.82

1. Argue that the Poisson–gamma models are appropriate for monthly rain-

fall data, along the lines of the argument in Sect. 12.2.4 (p. 463).

2. Perform a hypothesis test to address the relationship between rainfall and

soi given earlier in the question to see if it applies at Emerald: “Negative

values of the soi. . . are often associated with reduced rainfall in eastern

and northern Australia.”

3. Fit an appropriate edm for modelling the total monthly August rainfall

in Emerald from the soi.

4. Compute the 95% conﬁdence interval for the soi parameter, and deter-

mine the practical importance of soi for August rainfall in Emerald.

5. Fit an appropriate edm for modelling the total monthly August rainfall

in Emerald from the soi phases.

6. Interpret the ﬁtted model using soi phases, using the parameters of the

underlying Poisson and gamma distributions. (Hint: See (12.4), p. 464.)

12.6 Summary 485

Table 12.8 Data from 194 trawls in the South East Fisheries ecosystem regarding the

catch of tiger ﬂathead. Distance is measured north to south on the 100 m depth contour

(Problem 12.15)

Longitude Latitude Depth Distance Swept area Number of Biomass of tiger

of trawl of trawl (in m) (in m) (in ha) tiger ﬂathead ﬂathead (in kg)

149.06 −37.81 −33 91 4.72260 1 0.02

149.08 −37.83 −47 90 5.00040 0 0.00

149.11 −37.87 −74 89 6.11160 153 30.70

149.22 −38.02 −117 88 5.83380 15 7.77

149.27 −38.19 −212 88 3.04222 0 0.00

150.29 −37.41 −168 48 6.11160 25 6.90

150.19 −37.33 −113 48 5.83380 53 15.30

12.15. A study on the South East Fisheries ecosystem near Australia [4]

collected data about the number of ﬁsh caught from ﬁsh trawl surveys. One

analysis of these data [17] studied the number of tiger ﬂathead (Table 12.8;

data set: flathead).

1. The data record the number of ﬂathead caught per trawl plus the to-

tal biomass of the ﬂathead caught. Propose a mechanism for the total

biomass that leads to the Tweedie glm as a possible model (similar to

that used in Sect. 12.2.4).

2. The paper that analysed the data [17]ﬁtsaPoissonglm to model the

number of tiger ﬂathead caught. The paper states

...the dependence on covariates, if any, is speciﬁed using orthogonal polyno-

mials in the linear predictor. The dependency on depth used a second order

polynomial and the dependency on along-coast used a third order polyno-

mial. . . The log of the area swept variable was included as an oﬀset (p. 542).

Explain why area is used as an oﬀset.

3. Based on the information above, ﬁt an appropriate Poisson glm for mod-

elling the number of tiger ﬂathead caught (using Depth and Distance as

covariates, in the manner discussed in the quote above). Show that this

model has large overdispersion, and hence ﬁt a quasi-Poisson model. Pro-

pose a reason why overdispersion is observed.

4. Based on the above information, plot the logarithm of biomass against

the depth and distance, and comment on the relationships.

5. The paper that analysed the biomass data [17] stated that

There is no reason to include an extra spatial dimension. . . as it would be

highly confounded with depth (p. 541).

Determine if any such correlation exists between depth, and the latitude

and longitude.

486 12 Tweedie GLMs

Table 12.9 Feeding rates (in feeds per hour) of chestnut-crowed babblers (Prob-

lem 12.16)

Feeding Observation Chick Non-breeding Brood

rate time (h) Sex age (days) birds ages size

0.000 11.09 M 1 Adult 3

0.000 11.16 M 2 Adult 4

0.000 12.81 M 3 Adult 1

0.238 12.59 M 4 Adult 1

1.316 12.16 M 5 Adult 1

1.041 11.53 M 6 Adult 1

0.321 6.22 F 19 Adult 3

0.000 6.22 M 19 Yearling 3

6. The paper that analysed the biomass data [17] used a Tweedie glm (using

Depth and Distance as covariates, in the manner discussed in the quote

above). Based on the above information, ﬁt a suitable Tweedie glm,and

assess the model using diagnostics.

7. Compare the Q–Q plot of the deviance and quantile residuals from the

Tweedie glm, and comment.

12.16. Chestnut-crowned babblers are medium-sized Australian birds that

live in social groups. A study of their feeding habits [8] recorded, among

other things, the rates at which they fed, in feeds per hour (Table 12.9; data

set: babblers). About 18% of the feeding rates are exact zeros. Fit a Tweedie

glm to the data to model the feeding rates.

12.17. A study comparing two diﬀerent types of toothbrushes [2, 30] mea-

sured the plaque index for females and males before and after brushing

(Table 12.10; data set: toothbrush). Smaller values mean cleaner teeth. The

26 subjects all used both toothbrushes. One subject received the same plaque

index before and after brushing.

Assuming the plaque index cannot become worse after brushing, ﬁt an

appropriate glm to the data for modelling the diﬀerence (Before − After),

and deduce if the toothbrushes appear to diﬀer in their teeth-cleaning ability,

and if this seems related to the sex of the subject.

12.18. An experiment [3] to quantify the eﬀect of ketamine (an anaesthetic)

measured the amount of sleep (in min) for 30 guinea pigs, using ﬁve diﬀerent

doses (Table 12.11; data set: gpsleep).

1. Explain what the exact zeros mean.

2. Plot the data, and show that the variance increases with the mean.

3. Plot the logarithm of the group variances against the logarithm of the

group means, where the groups are deﬁned by the doses. Show this implies

ξ ≈ 1.

12.6 Summary 487

Table 12.10 The plaque index before and after brushing for two types of toothbrushes;

smaller values indicate cleaner teeth (Problem 12.17)

Conventional brush Hugger (new) brush

Females Males Females Males

Before After Before After Before After Before After

1.20 0.75 3.35 1.58 2.18 0.43 0.90 0.15

1.43 0.55 1.50 0.20 2.05 0.08 0.58 0.10

0.68 0.08 4.08 1.88 1.05 0.18 2.50 0.33

1.45 0.75 3.15 2.00 1.95 0.78 2.25 0.33

0.50 0.05 0.90 0.25 0.28 0.03 1.53 0.53

2.75 1.60 1.78 0.18 2.63 0.23 1.43 0.43

1.25 0.65 3.50 0.85 1.50 0.20 3.48 0.65

0.40 0.13 2.50 1.15 0.45 0.00 1.80 0.20

1.18 0.83 2.18 0.93 0.70 0.05 1.50 0.25

1.43 0.58 2.68 1.05 1.30 0.30 2.55 0.15

0.45 0.38 2.73 0.85 1.25 0.33 1.30 0.05

1.60 0.63 3.43 0.88 0.18 0.00 2.65 0.25

0.25 0.25 3.30 0.90

2.98 1.03 1.40 0.24

Table 12.11 Amount of sleep (in min) for 30 guinea pigs after receiving intravenous

dosesofketamine(Problem12.18)

0.60 mg/kg 1.04 mg/kg 1.44 mg/kg 2.00 mg/kg 2.75 mg/kg

0.00 0.00 0.00 0.00 0.00 3.60 5.59 7.67 0.00 1.71

0.00 0.00 2.85 5.92 8.32 8.50 9.40 9.77 11.15 11.89

3.99 4.78 7.36 10.43 12.73 13.20 10.92 24.80 14.48 14.75

4. Using tweedie.profile(), show that

ξ =1.1. (Hint: Try using xi.vec

= (1.02, 1.4, by=0.02) to ensure you obtain a good estimate of ξ.)

5. Show that a quadratic Tweedie glm in Dose is signiﬁcantly better than

the Tweedie glm linear is Dose.

6. Also consider the linear and quadratic Tweedie glm using log(Dose) in

place of Dose.

7. Also consider a Tweedie glm using a natural cubic spline, with knots=

quantile(Dose, c(0.33, 0.67))).

8. Plot all ﬁve systematic component on a plot of the data, and comment.

9. Use the aic to determine a model from the ﬁve considered, and show the

quadratic model in Dose is the preferred model.

488 REFERENCES

References

[1] Andrew, D.F., Herzberg, A.M.: Data: A Collection of Problems from

Many Fields for the Student and Research Worker. Springer, New York

(1985)

[2] Aoki, R., Achcar, J.A., Bolfarine, H., Singer, J.M.: Bayesian analysis

of null-intercept errors-in-variables regression for pretest/post-test data.

Journal of Applied Statistics 31(1), 3–12 (2003)

[3] Bailey, R.C., Summe, J.P., Hommer, L.D., McCracken, L.E.: A model

for the analysis of the anesthetic response. Biometrics 34(2), 223–232

(1978)

[4] Bax, N.J., Williams, A.: Habitat and ﬁsheries production in the South

East ﬁshery ecosystem. Final Report 1994/040, Fisheries Research and

Development Corporation (2000)

[5] Box, G.E.P.: Science and statistics. Journal of the American Statistical

Association 71, 791–799 (1976)

[6] Box, G.E.P., Cox, D.R.: An analysis of transformations (with discus-

sion). Journal of the Royal Statistical Society, Series B 26, 211–252

(1964)

[7] Brown, J.E., Dunn, P.K.: Comparisons of Tobit, linear, and Poisson-

gamma regression models: an application of time use data. Sociological

Methods & Research 40(3), 511–535 (2011)

[8] Browning, L.E., Patrick, S.C., Rollins, L.A., Griﬃth, S.C., Russell, A.F.:

Kin selection, not group augmentation, predicts helping in an obligate

cooperatively breeding bird. Proceedings of the Royal Society B 279,

3861–3869 (2012)

[9] Carr, L.J., Dunsiger, S.I., Marcus, B.H.: Validation of Walk Score for

estimating access to walkable amenities. British Journal of Sports

Medicine 45(14), 1144–1148 (2011)

[10] Cole, R., Dunn, P., Hunter, I., Owen, N., Sugiyama, T.: Walk score and

Australian adults’ home-based walking for transport. Health & Place

35, 60–65 (2015)

[11] Connolly, R.D., Schirmer, J., Dunn, P.K.: A daily rainfall disaggregation

model. Agricultural and Forest Meteorology 92(2), 105–117 (1998)

[12] Dunn, P.K.: Precipitation occurrence and amount can be modelled

simultaneously. International Journal of Climatology 24, 1231–1239

(2004)

[13] Dunn, P.K.: tweedie: Tweedie exponential family models (2017). URL

https://CRAN.R-project.org/package=tweedie. R package version 2.3.0

[14] Dunn, P.K., Smyth, G.K.: Randomized quantile residuals. Journal of

Computational and Graphical Statistics 5(3), 236–244 (1996)

[15] Dunn, P.K., Smyth, G.K.: Series evaluation of Tweedie exponential dis-

persion models. Statistics and Computing 15(4), 267–280 (2005)

REFERENCES 489

[16] Dunn, P.K., Smyth, G.K.: Evaluation of Tweedie exponential dispersion

models using Fourier inversion. Statistics and Computing 18(1), 73–86

(2008)

[17] Foster, S.D., Bravington, M.V.: A Poisson–gamma model for analysis of

ecological data. Environmental and Ecological Statistics 20(4), 533–552

(2013)

[18] Garby, L., Garrow, J.S., Jørgensen, B., Lammert, O., Madsen, K.,

Sørensen, P., Webster, J.: Relation between energy expenditure and body

composition in man: Speciﬁc energy expenditure in vivo of fat and fat-

free tissue. European Journal of Clinical Nutrition 42(4), 301–305 (1988)

[19] Gilchrist, R.: Regression models for data with a non-zero probability of

a zero response. Communications in Statistics—Theory and Methods

29, 1987–2003 (2000)

[20] Gilchrist, R., Drinkwater, D.: Fitting Tweedie models to data with prob-

ability of zero responses. In: H. Friedl, A. Berghold, G. Kauermann (eds.)

Statistical Modelling: Proceedings of the 14th International Workshop

on Statistical Modelling, pp. 207–214. International Workshop on Sta-

tistical Modelling, Gräz (1999)

[21] Hallin, M., François Ingenbleek, J.: The Swedish automobile portfolio in

1997. Scandinavian Actuarial Journal pp. 49–64 (1983)

[22] Hasan, M.M., Dunn, P.K.: A simple Poisson–gamma model for modelling

rainfall occurrence and amount simultaneously. Agricultural and Forest

Meteorology 150, 1319–1330 (2010)

[23] Jørgensen, B.: Exponential dispersion models (with discussion). Journal

of the Royal Statistical Society, Series B 49, 127–162 (1987)

[24] Jørgensen, B.: Exponential dispersion models and extensions: A review.

International Statistical Review 60(1), 5–20 (1992)

[25] Jørgensen, B.: The Theory of Dispersion Models. Monographs on Statis-

tics and Applied Probability. Chapman and Hall, London (1997)

[26] Jørgensen, B., de Souza, M.C.P.: Fitting Tweedie’s compound Poisson

model to insurance claims data. Scandinavian Actuarial Journal 1, 69–93

(1994)

[27] McBride, J.L., Nicholls, N.: Seasonal relationships between Australian

rainfall and the southern oscillation. Monthly Weather Review 111(10),

1998–2004 (1983)

[28] National Institute of Standards and Technology: Statistical reference

datasets (2016). URL http://www.itl.nist.gov/div898/strd

[29] Nelson, W.: Analysis of performance-degradation data from accelerated

tests. IEEE Transactions on Reliability 30(2), 149–155 (1981)

[30] Singer, J.M., Andrade, D.F.: Regression models for the analysis of

pretest/posttest data. Biometrics 53, 729–725 (1997)

490 REFERENCES

[31] Smyth, G.K.: Regression analysis of quantity data with exact zeros.

In: Proceedings of the Second Australia–Japan Workshop on Stochastic

Models in Engineering, Technology and Management, pp. 572–580. Tech-

nology Management Centre, University of Queensland, Brisbane (1996)

[32] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

[33] Smyth, G.K.: statmod: Statistical Modeling (2017). URL https://

CRAN.R-project.org/package=statmod. R package version 1.4.30. With

contributions from Yifang Hu, Peter Dunn, Belinda Phipson and Yun-

shun Chen.

[34] Smyth, G.K., Jørgensen, B.: Fitting Tweedie’s compound Poisson model

to insurance claims data: Dispersion modelling. In: Proceedings of the

52nd Session of the International Statistical Institute. Helsinki, Finland

(1999). Paper Meeting 68: Statistics and Insurance

[35] Stone, R.C., Auliciems, A.: soi phase relationships with rainfall in east-

ern Australia. International Journal of Climatology 12, 625–636 (1992)

[36] Taylor, L.R.: Aggregation, variance and the mean. Nature 189, 732–735

(1961)

[37] Tweedie, M.C.K.: The regression of the sample variance on the sample

mean. Journal of the London Mathematical Society 21, 22–28 (1946)

Chapter 13

Extra Problems

Practice is the best of all instructors.

Publilius Syrus [19, Number 439]

13.1 Introduction and Overview

In previous chapters, problems were supplied relevant to the material in that

chapter. In this ﬁnal chapter, we present a series of problems without the

chapter context, and often with less direction for modelling the data.

Problems

13.1. A study of pubertal timing of youths [5, Table III] tabulated the rela-

tionship between gender, when they matured, and the satisfaction with their

current weight (Table 13.1; data set: satiswt).

1. Identify the zero as either structural or sampling.

2. Find a suitable model for the data, ensuring an appropriate diagnostic

analysis.

3. Interpret the ﬁnal model.

13.2. The data in Table 13.2 (data set: toxo) give the proportion of the

population testing positive to toxoplasmosis y against the annual rainfall

(in mm) x for 34 cities in El Salvador [7]. Plot the data, and describe the

important features of the data. Then, ﬁnd a suitable model for the data.

(Hint: A complicated systematic component is necessary; see Problem 1.4.)

13.3. A study [15, 17] examined the eﬀects of boric acid, a compound in

household products and pesticides, on in utero embryo damage in mice

(Table 13.3; data set: boric). Find a suitable model for modelling the ef-

fect of bromic acid on in utero damage in mice.

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7_13

491

492 13 Extra Problems

Table 13.1 The number of youths classiﬁed by gender, when they matured, and their

own opinions about their weight (Problem 13.1)

Number who wish to be

Matured Thinner Same weight Heavier

Girls Late 91 171 74

Mid 1170 861 177

Early 84 36 0

Boys Late 87 164 101

Mid 418 1300 604

Early 46 127 15

Table 13.2 The proportion of people testing positive to toxoplasmosis in 34 cities in

El Salvador (Problem 13.2)

Rainfall (in mm) Proportion Sampled Rainfall (in mm) Proportion Sampled

1735 0.50 4 1770 0.61 54

1936 0.30 10 2240 0.44 9

2000 0.20 5 1620 0.28 18

1973 0.30 10 1756 0.17 12

1750 1.00 2 1650 0.00 1

1800 0.60 5 2250 0.73 11

1750 0.25 8 1796 0.53 77

2077 0.37 19 1890 0.47 51

1920 0.50 6 1871 0.44 16

1800 0.80 10 2063 0.56 82

2050 0.29 24 2100 0.69 13

1830 0.00 1 1918 0.54 43

1650 0.50 30 1834 0.71 75

2200 0.18 22 1780 0.61 13

2000 0.00 1 1900 0.30 10

1770 0.54 11 1976 0.17 6

1920 0.00 1 2292 0.62 37

13.4. In the Birth to Ten study (btt) from the greater Johannesburg–Soweto

metropolitan area of South Africa during 1990, all mothers of singleton births

(4019 births) who had a permanent address within a deﬁned area were inter-

viewed during a seven-week period between April and June 1990 [13]. (Sin-

gleton births are non-multiple births; that is, no twins, triplets, etc.) Five

years later, 964 of these mothers were re-interviewed.

For further research to be useful, the mothers not followed-up ﬁve years

later (Group 1) should have similar characteristics to those mothers who were

followed-up ﬁve years later (Group 2). One of the factors for comparison was

whether the mother had medical aid (similar to health insurance) at the time

of the birth of the child. Table 13.4 (data set: bttstudy) supplies these data

according to the mothers’ race.

13.1 Introduction and Overview 493

Table 13.3 The number of dead embryos D and total number of embryos T in mice at

various doses of boric acid (as percentage of feed) (Problem 13.3)

Dose 0.0 Dose 0.1 Dose 0.2 Dose 0.4

DT DT DT DT DT DT DT DT

0 15 0 8 0 6 0 13 1 12 0 10 12 12 3 12

0301311401001209 112221

1 9 2 14 1 12 1 12 0 11 1 12 0 13 3 10

112314010011013013 28311

113011214210012114 212111

213212012212014013 413111

016015014215415014 013814

011015314312014113 113015

111214010112012212 012213

2811121201216114 19811

014116313112213013 39412

013012111113010012 011212

31401411111511417 114

1 13 0 11 1 12 0 10

Table 13.4 Number of subjects whose mothers had medical aid by the race of the

participants (Problem 13.4)

White Black

Group 1 Group 2 Group 1 Group 2

Had medical aid 104 10 91 36

Had no medical aid 22 2 957 368

Total 126 12 1048 404

1. Compute the percentage of mothers in each group with medical aid.

Which group has a higher uptake of medical aid? (That is, produce a

two-way table of Group against whether or not the mother had medical

aid, combing both race categories.)

2. Compute the percentages of mothers in each group with and without

medical aid according to race. Which group has a higher uptake of medical

aid within each race? Contrast this with your answer above.

3. Explain the above paradox by ﬁtting and interpreting the appropriate

glm for the data.

13.5. In Example 4.4, data were given regarding the time to service soft drink

vending machine routes [12]. The main interest was in predicting the amount

of time y required by the route driver to service the vending machines in

an outlet. This service activity includes stocking the machine with beverage

products and minor maintenance or housekeeping. In that example, the two

most important variables were identiﬁed as the number of cases of product

stocked x

and the distance walked by the route driver x

(Table 4.2; data

set: sdrink).

494 13 Extra Problems

Table 13.5 Canadian insurance data (Problem 13.6)

Merit Class Insured Premium Claims Cost

3 1 2,757,520 159,108 217,151 63,191

3 2 130,535 7175 14,506 4598

3 3 247,424 15,663 31,964 9589

3 4 156,871 7694 22,884 7964

3 5 64,130 3241 6560 1752

2 1 130,706 7910 13,792 4055

2 2 7233 431 1001 380

2 3 15,868 1080 2695 701

2 4 17,707 888 3054 983

2 5 4039 209 487 114

1 1 163,544 9862 19,346 5552

1 2 9726 572 1430 439

1 3 20,369 1382 3546 1011

1 4 21,089 1052 3618 1281

1 5 4869 250 613 178

0 1 273,944 17,226 37,730 11,809

0 2 21,504 1207 3421 1088

0 3 37,666 2502 7565 2383

0 4 56,730 2756 11,345 3971

0 5 8601 461 1291 382

The dependence of time on the two covariates is likely to be directly linear,

as seen in Fig. 4.1, because time should increase linearly with the number of

cases or the distance walked. Fit a suitable glm for modelling the delivery

times.

13.6. A summary of the Canadian automobile insurance industry [1] for pol-

icy years 1956 and 1957 (as of June 30, 1959) are given in Table 13.5 (data

set: cins). Virtually every insurance company operating in Canada is repre-

sented. The data are for private passenger automobile liability for non-farmers

for all of Canada apart from Saskatchewan.

The factor Merit measures the number of years since the last policy claim

(see ?cins for the details). Class is a factor based on gender, age, use and

marital status (see ?cins for the details). Insured and Premium are two mea-

sures of the risk exposure of the insurance companies. Insured is measured in

earned car-years; that is, a car insured for 6 months is 0.5 car-years. Premium

is in thousands of dollars adjusted to the premium of cars written oﬀ at 2001

rates. The data also give the number of Claims and the total Cost of the

claims in thousands of dollars.

1. Fit a glm to model the number of claims.

2. Fit a glm to model the cost per claim.

3. Fit a glm to model the total cost.

In your models, you will need to consider using an oﬀset.

13.1 Introduction and Overview 495

Table 13.6 The number of revertant colonies for various doses of quinoline (in μgper

plate) (Problem 13.7)

Dose Colonies Dose Colonies Dose Colonies

0 15 33 16 333 33

0 21 33 26 333 38

0 29 33 33 333 41

10 16 100 27 1000 20

10 18 100 41 1000 27

10 21 100 60 1000 42

13.7. A study [2] used an Ames mutagenicity assay to count the number of

revertant colonies (colonies that revert back to the original genotype) of TA98

Salmonella in rat livers (Table 13.6; data set: mutagen). Theory [2] suggests

a good approximate model for the data is log(μ)=α + β log(d + c) − dγ for

dose d, where μ = E[Counts], γ ≥ 0, and c = 10 in this case.

1. Plot the data, using logarithm of dose on the horizontal axis.

2. Fit the suggested model to the data, and summarize. Plot this model

with the data.

3. Show that there is evidence of overdispersion.

4. Fit a negative binomial model (with the same systematic component) to

the data, and summarize.

5. Compare the two models graphically, including conﬁdence intervals for

the ﬁtted values.

13.8. To study the eﬀect of trout eggs and the toxin potassium cyanate

(kscn)[9, 14], the toxin was applied at six diﬀerent concentrations to vials of

ﬁsh eggs. Each vial contained between 61 and 179 eggs. The eggs in half of the

vials were allowed to water-harden for several hours after fertilization before

the kscn was applied. For the other vials, the toxin was applied immediately

after fertilization. The number of eggs in the vial after 19 days was recorded

(Table 13.7; data set: trout). Interest is in the eﬀect of kscn concentration

on trout egg mortality.

Find an appropriate model for the proportion of eggs that do not survive,

ensuring an appropriate diagnostic analysis. Interpret the model.

13.9. In 1990, the Water Board of New South Wales, Australia, gathered

self-reported data from swimmers (Table 13.8; data set: earinf) about the

number of self-diagnosed ear infections after swimming [9, 18] to determine

if beach swimmers were more or less likely to report ear infections than non-

beach swimmers. Swimmers reported their age group (Age, with levels 15-19,

20-24 or 25-29), sex (Sex with levels Male or Female), and the number of

self-diagnosed ear infections (NumInfec), where they usually swam (Loc

, with

levels Beach or NonBeach), and whether they were a frequent ocean swimmer

(Swim, with levels Freq (frequent) or Occas (occasional)).

496 13 Extra Problems

Table 13.7 The eﬀect on potassium cyanate concentration (in mg/L) on the mortality

of trout eggs (Problem 13.8)

Water No water Water No water

hardening hardening hardening hardening

Conc. Number Dead Number Dead Conc. Number Dead Number Dead

90 111 8 130 7 720 83 2 99 29

97 10 179 25 87 3 109 53

108 10 126 5 118 16 99 40

122 9 129 3 100 9 70 0

180 68 4 114 12 1440 140 60 100 14

109 6 149 4 114 47 127 10

109 11 121 4 103 49 132 8

118 6 105 0 110 20 113 3

360 98 6 102 4 2880 143 79 145 113

110 5 145 21 131 85 103 84

129 9 61 1 111 78 143 105

103 17 118 3 111 74 102 78

Table 13.8 The number of self-reported ear infections from swimmers (Problem 13.9)

Males Females

Frequency Usual Number Frequency Usual Number

of ocean swimming Age of of ocean swimming Age of

swimming location group infections swimming location group infections

Occasional Non-beach 15–19 0 Occasional Non-beach 15–19 0

Occasional Non-beach 15–19 0 Occasional Non-beach 15–19 4

Occasional Non-beach 15–19 0 Occasional Non-beach 15–19 10

Occasional Non-beach 15–19 0 Occasional Non-beach 20–24 0

Frequent Beach 25–29 2 Frequent Beach 25–29 2

The purpose of the study is to understand the factors that inﬂuence the

number of ear infections. Find a suitable model for the data, and interpret

this model.

13.10. A study of the root system of apple trees [6, 16] used three diﬀer-

ent root stocks (Rstock with levels M26, Mark and MM106) and two diﬀerent

spacing (Spacing, with levels 4x2 and 5x3) for eight apple trees (Plant).

Soil core samples were analysed, classiﬁed as coming from the inner or outer

zone (Zone, with levels Inner and Outer respectively) relative to each plant

(Table 13.9; data set: fineroot). The response variable is the density of ﬁne

roots (the root length density, RLD, in cm/cm

); 38% of the RLD values are

zero.

13.1 Introduction and Overview 497

Table 13.9 The root length density (rld) of apple trees, rounded to two decimals

places (Problem 13.10)

M26 Mark MM106

Plant Spacing Zone rld Plant Spacing Zone rld Plant Spacing Zone rld

74× 2Outer0 1 5× 3 Inner 0 5 5 ×3Outer0

74× 2 Inner 0 1 5 ×3Outer0 5 5× 3Outer0

74× 2Outer0 1 5× 3 Inner 0 5 5 ×3Outer0

74× 2 Inner 0 1 5 ×3Outer0 5 5× 3Outer0

74× 2Outer0 1 5× 3 Inner 0 5 5 ×3 Inner 0

74× 2 Inner 0 1 5 ×3Outer0 5 5× 3Outer0

84× 2 Outer 0.42 4 4 × 2 Inner 0.30 6 5 × 3 Outer 0.48

84× 2 Inner 0.54 4 4 × 2 Inner 0.36 6 5 × 3 Outer 0.60

The design is not a full factorial design: not all plants are used with each

root stock and spacing. The Mark rootstock is used with both plant spacings,

but the other rootstocks are used at only one spacing each (M26 at 4x2,and

MM106 at 5x3).

1. Plot the data and describe the potential relationships.

2. Zone is the only variable varying within Plant, so initially ﬁt the model

with Plant and Zone, and possibly the interaction. Find an estimate of

ξ, then ﬁt the corresponding Tweedie glm.

3. Show that the model predicts the probability of zero rld well, but slightly

underestimates the probability for small values

4. Between plants, Rstock and Spacing vary. First, consider a Tweedie glm

with only Rstock and Zone together in the model (using the previously

estimated value of ξ). Then add Spacing, Plant and their interaction,

plus the Plant:Zone interaction to the model, and show only Rstock and

Zone and the interaction are necessary in the model.

5. Deduce a possible model for the data, ensuring a diagnostic analysis.

6. For the ﬁnal model, examine the mean rld for each rootstock–zone com-

bination, and interpret.

13.11. A study of the time it takes mammals of various masses to urinate [21]

found that

mammals above 3 kg in weight empty their bladders over nearly constant duration

(p. 11,932).

In other words, the mass of the mammal is not related to urination time.

The theory presented in the paper suggests that the authors were expecting

a relationship between duration D of urination and the mass M of the form

D = kM

1/3

for some proportionality constant k (data set: urinationD).

1. By using a transformation, ﬁt an appropriate weighted linear regression

model to all the data, and estimate the relationship between D and M.

498 13 Extra Problems

Table 13.10 The number of live births and number of Downs Syndrome births for

mothers in various age groups in British Columbia from 1961–1970 (Problem 13.12)

Mean Live Downs Synd. Mean Live Downs Synd. Mean Live Downs Synd.

age births cases age births cases age births cases

17.0 13,555 16 27.5 19,202 27 37.5 5780 17

18.5 13,675 15 28.5 17,450 14 38.5 4834 15

19.0 18,752 16 29.5 15,685 9 39.5 3961 30

20.5 22,005 22 30.5 13,954 12 40.5 2952 31

21.5 23,896 16 31.5 11,987 12 41.5 2276 33

22.5 24,667 12 32.5 10,983 18 42.4 1589 20

23.5 24,807 17 33.5 9825 13 43.5 1018 16

24.5 23,986 22 34.5 8483 11 44.5 596 22

25.5 22,860 15 35.5 7448 23 45.5 327 11

26.5 21,450 14 36.5 6628 13 47.0 249 7

2. The paper suggests that no relationship exists between D and M for

mammals heavier than 3 kg. Determine if those observation appear as

inﬂuential in the ﬁtted model above.

3. Fit the same model as above, but to mammals heavier than 3 kg only, as

suggested by the quotation above. Are the paper’s conclusions supported?

13.12. The number of Downs Syndrome births in British Columbia, Canada,

from 1961–1970 is tabulated in Table 13.10 (data set: downs)[4, 8]. Fit an

appropriate glm to model the number of Downs Syndrome cases, and plot

the systematic component on the plot of the data. Then, ﬁt an appropriate

glm to model the proportion of Downs Syndrome cases as a function of age.

Comment on the similarities and diﬀerences between the two models.

13.13. Blood haematology in athletes is of interest and importance at the

elite level. To this end, the Australian Institute of Sport (AIS) gathered

haematological information from 202 elite athletes across various sports [20]

(data set: AIS). The aim of the study was stated as follows:

The main aim of the statistical analysis was to determine whether there were any

hematological diﬀerences, on average, between athletes from the various sports,

between the sexes, and whether there was an eﬀect of mass or height (p. 789).

Use the data to provide information for answering this question, focussing on

haemoglobin concentration.

13.14. A study [11] exposed 96 rainbow trout to various concentrations of 3,

4-dichloroaniline (DCA). After 28 days, the weights of the trout were recorded

(Table 13.11; data set: rtrout). The aim of the study was to “determine the

concentration level which causes 25% inhibition [i.e. weight loss] from the

control” [3, p. 161]. One analysis of the data [3] used a gamma glm with a

quadratic systematic component.

13.1 Introduction and Overview 499

Table 13.11 The weight of rainbow trout (in grams) at various doses of DCA (in μg

per litre) (Problem 13.14)

Dose of DCA (in μg per litre)

Control 19 39 71 120 210

12.7 9.4 12.7 11.9 7.7 8.8

13.3 13.9 9.2 13.2 6.4 8.7

16.3 16.4 10.4 10.5 9.8 8.6

13.8 11.8 15.3 9.5 8.8 7.3

8.7 15.0 13.3 12.5 9.9 8.6

13.6 14.3 11.1 10.4 11.1 11.4

10.6 11.0 9.4 13.1 12.1 9.9

13.8 15.0 8.2 8.4 10.5 7.3

12.5 12.2 13.2 10.6 9.0 10.6

14.7 13.3 12.1 11.3 13.7 8.4

10.9 12.3 7.9 9.6 8.4 7.4

8.9 7.0 15.3 9.1 7.6 8.3

12.7 11.3 9.6 10.6 11.0 8.5

13.0 11.8 15.5 7.4 7.8

9.1 14.6 15.3 9.6 9.7 10.1

13.7 12.4 8.2 10.3 9.5 8.2

Fit and evaluate the ﬁtted model, suggesting another model if appropriate.

Then, using this model, estimate the dose as described in the aim.

13.15. Consider the Galápagos Islands species data (Table 13.12; data set:

galapagos)[10]. Find factors that seem to inﬂuence (a) the number of en-

demic species, and (b) the proportion of the species on each island which are

endemic. Summarize your results. Here are some hints:

• The number of species, and the proportion of endemics, are obviously

non-normal variables. You will need to choose appropriate response dis-

tributions for them.

• All of the explanatory variables are highly skew, and no regression method

could be expected to be successful without transforming them. Whenever

an explanatory variable is strictly positive and varies by a factor of 10 or

more, it is a good idea to pre-emptively apply a logarithmic transforma-

tion before undertaking any analysis. Even if the logarithmic transforma-

tion doesn’t eventually turn out to the best transformation, it will be a

big step in the right direction. For a variable like StCruz which contains

an exact zero, you could use log(StCruz+0.1), where 0.1 is the smallest

unit in which the distances are recorded.

500 REFERENCES

Table 13.12 The Galápagos Islands species data. See the help ﬁle (?galapagos)for

information on the variables (Problem 13.15)

Island

Plants

PlantEnd

Finches

FinchEnd

FinchGenera

Area

Elevation

Nearest

StCruz

Adjacent

Baltra 58 23 4 25.09 100 0.6 0.6 1.84

Bartolome 31 21 1.24 109 0.6 26.3 572.33

Caldwell 3 3 0.21 114 2.8 58.7 0.78

Champion 25 9 0.10 46 1.9 47.4 0.18

Coamano 2 1 0.05 25 1.9 1.9 903.82

Daphne Major 18 11 0.34 50 8.0 8.0 1.84

Darwin 10 7 4 2 2 2.33 168 34.1 290.2 2.85

Eden 8 4 0.03 50 0.4 0.4 17.95

Enderby 2 2 0.18 112 2.6 50.2 0.10

Espanola 97 26 3 2 2 58.27 198 1.1 88.3 0.57

Fernandina 93 35 9 0 5 634.49 1494 4.3 95.3 4669.32

Gardner (near Española) 58 17 0.57 49 1.1 93.1 58.27

Gardner (near Santa Maria) 5 4 0.78 227 4.6 62.2 0.21

Genovesa 40 19 4 3 2 17.35 76 47.4 92.2 129.49

Isabela 347 89 10 1 5 4669.32 1707 0.7 28.1 634.49

Marchena 51 23 7 1 4 129.49 343 29.1 85.9 59.56

Onslow 2 2 0.01 25 3.3 45.9 0.10

Pinta 104 37 9 2 4 59.56 777 29.1 119.6 129.49

Pinzon 108 33 9 0 5 17.95 458 10.7 10.7 0.03

Las Plazas 12 9 0.23 50 0.5 0.6 25.09

Rabida 70 30 9 0 5 4.89 367 4.4 24.4 572.33

San Cristobal 280 65 7 3 5 551.62 716 45.2 66.5 0.57

San Salvador 237 81 10 0 5 572.33 906 0.2 19.8 4.89

Santa Cruz 444 95 10 0 5 903.82 864 0.6 0.0 0.52

Santa Fe 62 28 7 1 3 24.08 259 16.5 16.5 0.52

Santa Maria 285 73 9 2 4 170.92 640 2.6 49.2 0.10

Seymour 44 16 1.84 50 0.6 9.6 25.09

Tortuga 16 8 1.24 186 6.8 50.9 17.95

Wolf 21 12 5 1 2 2.85 253 34.1 254.7 2.33

References

[1] Bailey, R.A., Simon, L.J.: Two studies in automobile insurance ratemak-

ing. ASTIN Bulletin I(IV), 192–217 (1960)

[2] Breslow, N.E.: Extra-Poisson variation in log-linear models. Applied

Statistics 33(1), 38–44 (1984)

[3] Crossland, N.O.: A method to evaluate eﬀects of toxic chemicals on ﬁsh

growth. Chemosphere 14(11–12), 1855–1870 (1985)

[4] Davison, A.C., Hinkley, D.V.: Bootstrap Methods and their Application.

Cambridge University Press (1997)

REFERENCES 501

[5] Duncan, P.D., Ritter, P.L., Dornbusch, S.M., Gross, R.T., Carlsmith,

J.M.: The eﬀects of pubertal timing on body image, school behavior,

and deviance. Journal of Youth and Adolescence 14(3), 227–235 (1985)

[6] Dunn, P.K., Smyth, G.K.: Series evaluation of Tweedie exponential dis-

persion models. Statistics and Computing 15(4), 267–280 (2005)

[7] Efron, B.: Double exponential families and their use in generalized linear

regression. Journal of the American Statistical Association 81(395), 709–

721 (1986)

[8] Geyer, C.J.: Constrained maximum likelihood exempliﬁed by isotonic

convex logistic regression. Journal of the American Statistical Associa-

tion 86(415), 717–724 (1991)

[9] Hand, D.J., Daly, F., Lunn, A.D., McConway, K.Y., Ostrowski, E.: A

Handbook of Small Data Sets. Chapman and Hall, London (1996)

[10] Johnson, M.P., Raven, P.H.: Species number and endemism: The Galá-

pagos Archipelago revisited. Science 179(4076), 893–895 (1973)

[11] Maul, A.: Application of generalized linear models to the analysis of

toxicity test data. Environmental Monitoring and Assessment 23(1),

153–163 (1992)

[12] Montgomery, D.C., Peck, E.A.: Introduction to Regression Analysis. Wi-

ley, New York (1992)

[13] Morrell, C.H.: Simpson’s paradox: An example from a longitudinal study

in South Africa. Journal of Statistics Education 7 (3) (1999)

[14] O’Hara Hines, R.J., Carter, M.: Improved added variable and partial

residual plots for the detection of inﬂuential observations in generalized

linear models. Applied Statistics 42(1), 3–20 (1993)

[15] Price, J.J., Field, C.J., Field, E.A., Marr, M.C., Myers, C.B., Morrisse,

R.E., Schwetz, B.A.: Developmental toxicity of boric acid in mice and

rats. Fundamental and Applied Toxicology 18, 266–277 (1992)

[16] de Silva, H.N., Hall, A.J., Tustin, D.S., Gandar, P.W.: Analysis of dis-

tribution of root length density of apple trees on diﬀerent dwarﬁng root-

stocks. Annals of Botany 83, 335–345 (1999)

[17] Slaton, T.L., Piergorsch, W.W., Durham, S.D.: Estimation and testing

with overdispersed proportions using the beta-logistic regression model

of Heckman and Willis. Biometrics 56(1), 125–133 (2000)

[18] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011).

URL http://www.statsci.org/data

[19] Publius Syrus: The Moral Sayings of Publius Syrus, a Roman Slave: from

the Latin. L. E. Bernard & co (Translated by Darius Lyman) (1856)

[20] Telford, R.D., Cunningham, R.B.: Sex, sport, and body-size dependency

of hematology in highly trained athletes. Medicine and Science in Sports

and Exercise 23(7), 788–794 (1991)

[21] Yang, P.J., Pham, J., Choo, J., Hu, D.L.: Duration of urination does not

change with body size. Proceedings of the National Academy of Sciences

111(33), 11 932–11 937 (2014)

Appendix A

Using R for Data Analysis

The data analyst knows more than the computer.

Henderson and Velleman [7, p. 391]

A.1 Introduction and Overview

This chapter introduces the r software package. We start by discussing how

to obtain and install r and the r packages needed for this book (Sect. A.2).

We then introduce the basic use of r, including working with vectors, loading

data, and writing functions in r (Sect. A.3).

A.2 Preparing to Use R

A.2.1 Introduction to R

r is a powerful and convenient tool for ﬁtting the models presented in this

book. Rather than a menu-driven statistical package, r is a powerful envi-

ronment for statistically and graphically analyzing data. r is free to install

and use.

While r itself is not a menu-driven package, some graphical front-ends

are available, such as r Commander [4, 5, 6](http://www.rcommander.

com/). RStudio (https://www.rstudio.com/products/RStudio/) provides an

environment for working with r which includes an integrated console, cod-

ing, graphics and help windows. R Commander is free, and free versions of

RStudio also exist.

The use of r is explained progressively throughout this book for use with

linear regression models and glms. In this appendix, some basics of using r

are described. A more comprehensive treatment of using r can be found in

the following books, among others:

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7

503

504 Appendix A

• Dalgaard [1] is a gentle introduction to using r for basic statistics.

• Maindonald and Braun [8] introduces r and covers a variety of statistical

techniques.

• Venables and Ripley [13] is an authoritative book discussing the imple-

mentation of a variety of statistical techniques in r and the closely-related

commercial program S-Plus.

A.2.2 Important R Websites

Two websites are particularly important for r users:

•Ther Project for Statistical Computing (http://www.r-project.org/)is

the r homepage. This web site contains documentation, general informa-

tion, links to searchable r mailing list archives, and much more.

• The Comprehensive r Archive Network, known as cran, contains the

ﬁles necessary for downloading r and add-on packages. A link to cran

is given from the r homepage: go to the r homepage, and select cran

from the menu. Clicking this link forces the user to select a mirror site.

(Selecting a mirror site near to you may make for faster downloads.)

Clicking on an appropriate mirror site then directs the browser to cran,

where r can be downloaded.

Another useful webpage is rseek.org, which provides a search facility dedi-

cated to r.

A.2.3 Obtaining and Installing R

r can be downloaded from cran (follow the instructions in Sect. A.2.2 to

locate cran). The procedure for then installing r depends on your operating

system (Windows; Mac OS X; linux; etc.). The easiest approach for most

users is to go to cran, then click on ‘Download and Install R’, then download

the pre-compiled binaries for your operating system. Then install these pre-

compiled binaries in the usual way for your operating system.

cran maintains current documentation for installing r. Click on the ‘Man-

uals’ link on the left (on either the cran website or the r homepage), and

read the manual R Installation and Administration. (Another manual, the

document An Introduction to R, may also prove useful for learning to use r.)

A.2.4 Downloading and Installing R Packages

Packages are collections of r functions that add extra functionality to r.

Some packages come with r, but other packages must be separately down-

loaded and installed before use. An important package used in this book

is the GLMsData package [3], which contains the data sets used in this

book. Using the r code in this book requires the GLMsData package to be

Appendix A 505

downloaded and installed, so we demonstrate the process of downloading and

installation of r packages using the GLMsData packages. More information

about the GLMsData package appears in Appendix B (p. 525).

For Windows and Mac OS X users, packages can be installed by starting

r and using the menu system:

Windows: Click Packages, then Install package(s). Select a cran mirror, then

select the package you wish to install, and then press OK.

Mac OS X: Click Packages & Data, and select CRAN (binaries) from the drop-

down menu. Clicking Get List creates a list of the packages that can be

installed from cran; make your selection, then press Update All.

Users of RStudio can install packages through the RStudio menus (under

Tools).

Alternatively, packages can be downloaded directly from cran; Sect. A.2.2

contain instructions to locate your nearest cran mirror. From the cran

homepage, select ‘Packages’, then locate and click on the name of the package

you wish to install. Here, we use the package GLMsData to demonstrate, but

the instructions are the same for downloading any r package. After clicking

on the package name in the cran list, click on the ﬁle to download for

your operating system (for example, Windows users click on the ﬁle next to

‘Windows binary’). The ﬁle will be then downloaded. To then install:

• Windows: Choose Packages from the Menu, then Install p ackage(s) from

local zip ﬁles. . . . Locate the package to install.

• Mac OS X: Click Packages & Data, select Local Binary Package, then press

Install.... Locate the package to install.

• Linux: Open a terminal and type sudo R CMD INSTALL GLMsData,for

example, in the directory where the package was downloaded, assuming

the appropriate permissions exist.

Packages can also be installed using install.packages() from the r com-

mand line; for example, install.packages("GLMsData"). Reading the doc-

ument R Installation and Administration, available at http://cran.r-project.

org/doc/manuals/R-admin.pdf, may prove useful.

A.2.5 Using R Packages

Any package, whether downloaded and installed or a package that comes

with r,mustbeloaded before being used in any r session:

• Loading: To load an installed package and so make the extra func-

tionality available to r, type (for example) library(GLMsData) (or

library("GLMsData"))atther prompt.

• Using: After loading the package, the functions in the package can be

used like any other function or data set in r.

• Obtaining help: To obtain help about the GLMsData package, even

if the package is not loaded (but is installed), type library(help=

506 Appendix A

GLMsData) (or library(help="GLMsData"))atther prompt. To ob-

tain help about particular function or data set in the package, type (for

example) ?lungcap at the r prompt after the package is loaded.

A.2.6 The R Packages Used in This Book

We have purposely kept the number of packages needed for this book to a

minimum. These packages are used in this book:

GLMsData:TheGLMsData package [3] is essential for running the r code

in this book, as it provides most of the necessary data.

MASS:TheMASS package [13] supplies the boxcox() function (Sect. 3.9),

the dose.p() function and functions used for ﬁtting negative binomial

glms (Sect. 10.5.2). MASS comes with all r distributions, and does not

need to be downloaded and installed as described above.

splines:Thesplines package [10] is used to ﬁt regression splines (Sect. 3.12).

splines comes with all r distributions, and does not need to be down-

loaded and installed as described above.

statmod:Thestatmod package [12] provides the tweedie() family function

used to ﬁt Tweedie glms (Chap. 12), for computing quantile residuals

(Sect. 8.3.4), and for evaluating the probability function for the inverse

Gaussian distribution. statmod does not come with r distributions, and

must be downloaded and installed as described above.

tweedie:Thetweedie package [2] provides functions for estimating the

Tweedie index parameter ξ for ﬁtting Tweedie glms, is used by qresid()

to compute quantile residuals for Tweedie glms, and is used for other

computations related to Tweedie glms (Chap. 12,p.457). tweedie does

not come with r distributions, and must be downloaded and installed as

described above.

The packages are loaded for use (after being downloaded and installed if

necessary) by typing

library(statmod) (for example) at the r prompt.

A.3 Introduction to Using R

A.3.1 Basic Use of R as an Advanced Calculator

After starting r, a command line is presented indicating that r is waiting for

the user to enter commands. This command line usually looks like this:

Instruct r to perform basic arithmetic by issuing commands at the command

line, and pressing the Enter or Return key. After starting r, enter this

command, and then press Enter (do not type the > as this is the r prompt):

>2-9*(1-3)

Appendix A 507

Note that * indicates multiplication. r responds with the answer:

[1] 20

After giving the answer, r then awaits your next instruction. Note that the

answer here is preceded by [1], which indicates the ﬁrst item of output, and

is of little use here where the output consists of one number. Sometimes r

produces many numbers as output, when the [1] proves useful, as seen later

(Sect. A.3.5). Other examples:

>2*pi #piis3.1415...

[1] 6.283185

> -8 + ( 2^3 ) # 2^3 means 2 raised to the power 3

[1] 0

> 10/4000000 # 10 divided by a big number

[1] 2.5e-06

>1+2*3 #Note the order of operations

[1] 7

Note the use of #:the# character is a comment character, so that # and

all text after it is ignored by r. (You don’t need to type the # or the text

that follows.) The output from the ﬁnal expression 2.5e-06 is r’s way of

displaying 2.5 ×10

−6

. Very large or very small numbers can be entered using

this notation also:

> 6.02e23 # Avogadro constant

[1] 6.02e+23

Standard mathematical functions are also deﬁned in r:

> exp( 1 ) # exp(x) means e raised to the power x where e = 2.71828...

[1] 2.718282

> log( 10 ) # Notice that log is the natural log

[1] 2.302585

> log10( 10 ) # This is log to base 10

[1] 1

> log2(32) # This is log to base 2

[1] 5

> sin( pi ) # The result is zero to computer precision

[1] 1.224647e-16

> sqrt( 45 ) # The square root

[1] 6.708204

Issuing incomplete r commands forces r to wait for the command to be

completed. Suppose you wish to evaluate 2*pi*7.4, but enter this in-

complete command:

>2*pi*

508 Appendix A

r will continue to wait for you to complete the command. The prompt changes

from > to + to indicate r is waiting for further input. Continue by entering

7.4 and pressing Return. The complete interaction looks like this:

>2*pi*

+ 7.4 # DO NOT type the "+" sign: R is asking for more info

[1] 46.49557

Note that 2*piis a complete command, so if 2*piis issued at the r

prompt, r provides the answer and does not expect any further input.

A.3.2 Quitting R

To ﬁnish using r, enter the command q() at the command prompt:

> q() # This will close R

The empty parentheses are necessary. r asks if you wish to Save workspace

image? If you respond with Yes, then r will save your work, so that next time

r is started you can continue your previous r session. If you respond with

No, r starts a fresh session the next time r is started.

A.3.3 Obtaining Help in R

The following commands can be used to obtain help in r:

• help.search("glm"): search the r help system for the text glm.

• ?glm: obtain help for the function glm(); equivalent to help("glm").

• help.start(): opens r’s on-line documentation in a browser.

• RSiteSearch("generalized linear model"), if you are connected to

the Internet: Search wider r resources, such as r-help mailing list

archives, r manuals and r help pages, and displays the results in a

browser window.

• example("glm"): show an example of using glm().

A.3.4 Variable Names in R

Importantly, answers computed by r can be assigned to variables using the

two-character combination <- as shown below:

> radius <- 0.605

> area <- pi * radius^2

> area

[1] 1.149901

Appendix A 509

Notice that when <- is used, the answer is not displayed. Typing the name

of a variable shows its value. The equal sign = canbeusedinplaceof<- to

make assignments, though <- is traditional:

> radius = 0.605

Spacing in the input is not important to r. All these commands mean the

same to r, but the ﬁrst is easiest to read and is recommended:

> area <- pi * radius^2

> area <- pi *radius^ 2

> area<-pi*radius^2

Variable names can consist of letters, digits, the underscore character, and

the dot (period). Variable names cannot start with digits; names starting

with dots should be avoided. Variable names are also case sensitive: HT, Ht

and ht are diﬀerent variables. Many possible variables names are already in

use by r, such as log as used above. Problems may result if these are used as

variable names. Common variables names to avoid include t (for transposing

matrices), c (used for combining objects), q (for quitting r), T (is a logical

true), F (is a logical false), and data (makes data sets available to r).

These are all valid variables names: plant.height, dose2, Initial_Dose,

PatientAge,andcircuit.2.AM. In contrast, these are not valid variables

names: Before-After (the - is illegal), and 2ndTrial (starts with a digit).

A.3.5 Working with Vectors in R

r works especially well with a group of numbers, called a vector. Vectors are

created by grouping items together using the function c() (for ‘combine’ or

‘concatenate’):

> x <- c(1, 2, 3, 4, 5, 6, 7, 8, 9, 10)

> log(x)

[1] 0.0000000 0.6931472 1.0986123 1.3862944 1.6094379 1.7917595 1.9459101

[8] 2.0794415 2.1972246 2.3025851

Notice that when the output is long, r identiﬁes the element of each list in

the left column, starting with [1]. Element 8 (which is 2.0794415) starts

the second line of output.

A long sequence of equally-spaced values is often useful, especially in plot-

ting. Rather than the cumbersome approach adopted above, consider these

simpler approaches:

> seq(0, 10, by=1) # The values are separated by distance 1

[1]012345678910

> 0:10 # Same as above

[1]012345678910

> seq(0, 10, length=9) # The result has length 9

[1] 0.00 1.25 2.50 3.75 5.00 6.25 7.50 8.75 10.00

510 Appendix A

Variables do not have to be numerical to be grouped together; text and

logical variables can be used also:

> day <- c("Sun", "Mon", "Tues", "Wed", "Thurs", "Fri", "Sat")

> hours.work <- c(0, 8, 11.5, 9.5, 8, 8, 3)

> hours.sleep <- c(8, 8, 9, 8.5, 6, 7, 8)

> do.exercise <- c(TRUE, TRUE, TRUE, FALSE, TRUE, FALSE, TRUE)

> hours.play <- 24 - hours.work - hours.sleep

> hours.awake <- hours.work + hours.play

Single or double quotes are possible for deﬁning text variables, though double

quotes are preferred (which enables constructs like "O’Neil" and "Don’t

know").

Speciﬁc elements of a vector are identiﬁed using square brackets:

> hours.play[3]; day[ 2 ]

[1] 3.5

[1] "Mon"

As shown, commands can be issued together on one line if separated by a

; (a semi-colon). To ﬁnd the value of hours.work on Fridays, consider the

following:

> day == "Fri" # A logic statement

[1] FALSE FALSE FALSE FALSE FALSE TRUE FALSE

> hours.work[ day == "Fri" ]

[1] 8

> hours.sleep[ day == "Fri" ]

[1] 7

> do.exercise[ day == "Thurs"]

[1] TRUE

Notice that == is used for logical comparisons. Other logical comparisons are

also possible:

> day[ hours.work>8] # > means "greater than"

[1] "Tues" "Wed"

> day[ hours.sleep<8] # < means "less than"

[1] "Thurs" "Fri"

> day[ hours.work >= 8 ] # >= means "greater than or equal to"

[1] "Mon" "Tues" "Wed" "Thurs" "Fri"

> day[ hours.work <= 8 ] # <= means "less than or equal to"

[1] "Sun" "Mon" "Thurs" "Fri" "Sat"

> day[ hours.work != 8 ] # != means "not equal to"

[1] "Sun" "Tues" "Wed" "Sat"

> day[ do.exercise & hours.work>8 ] # & means "and"

[1] "Tues"

> day[ hours.play>9 | hours.sleep>9 ] # | means "or"

[1] "Sun" "Thurs" "Sat"

Appendix A 511

Comparing real numbers using == should be avoided, because of the way com-

puters store ﬂoating-point numbers. (This is true for all computer languages.)

Instead, use all.equal():

> expr1 <- 0.5 - 0.3 # These two expressions should be the same

> expr2 <- 0.3 - 0.1

> c(expr1, expr2) # They *look* the same, but...

[1] 0.2 0.2

> expr1 == expr2 # ...Not exactly the same in computer arithmetic

[1] FALSE

> all.equal(expr1, expr2) # ...so use all.equal()

[1] TRUE

A.3.6 Loading Data into R

In statistics, data are usually stored in computer ﬁles, which must be loaded

into r. r requires data ﬁles to be arranged with variables in columns, and

cases in rows. Columns may have headers containing variable names; rows

may have headers containing case labels.

In r, data are usually treated as a data frame, a set of variables (nu-

meric, text, logical, or other types) grouped together. For the data entered

in Sect. A.3.5, a single data frame named my.week could be constructed:

> my.week <- data.frame(day, hours.work, hours.sleep,

do.exercise, hours.play, hours.awake)

> my.week

day hours.work hours.sleep do.exercise hours.play hours.awake

1 Sun 0.0 8.0 TRUE 16.0 16.0

2 Mon 8.0 8.0 TRUE 8.0 16.0

3 Tues 11.5 9.0 TRUE 3.5 15.0

4 Wed 9.5 8.5 FALSE 6.0 15.5

5 Thurs 8.0 6.0 TRUE 10.0 18.0

6 Fri 8.0 7.0 FALSE 9.0 17.0

7 Sat 3.0 8.0 TRUE 13.0 16.0

Entering data directly into r is only feasible for small amounts of data (and

is demonstrated, for example, in Sect. 10.4.2). Usually, other methods are

used for loading data into r:

1. If the data set comes with r, load the data using the command

data(trees) (for example), as in Example 3.14 (p. 125). Type data()

at the r prompt to see a list of all the data ﬁles that come with r.

2. If the data are in an installed r package (Sect. A.2.5), load the package,

then use data() to load the data. For example (assuming the GLMsData

is installed), load the package by typing library(GLMsData), then load

the data frame lungcap using data(lungcap) (Sect. 1.1).

512 Appendix A

3. If the data are stored as a text ﬁle (either on a storage device or on the

Internet), r provides a set of functions for loading the data:

read.csv(): Reads comma-separated text ﬁles. In ﬁles where the comma

is a decimal point and ﬁelds are separated by a semicolon, use read.

csv2().

read.delim(): Reads delimited text ﬁles, where ﬁelds are delimited by

tabs by default. In ﬁles where the comma is a decimal point, use

read.delim2().

read.table(): Reads ﬁles where the data in each line is separated by

one or more spaces, tabs, newlines or carriage returns. read.table()

has numerous options for reading delimited ﬁles.

read.fwf(): Reads data from ﬁles where the data are in a fixed width

format (that is, the data are in ﬁelds of known widths in each line of

the data ﬁle).

These functions are used by typing, for example:

> mydata <- read.csv("filename.csv")

Many other inputs are also available for these functions (see the relevant

help ﬁles). All these functions load the data into r as a data frame. These

functions can be used to load data directly from a web page (providing

you are connected to the Internet) by providing the url as the ﬁlename.

For example, the data in Table 10.20 (p. 420) are also found in tab-

delimited format at the Ozdasl webpage [11], with variable names in the

ﬁrst row (called a header):

> modes <- read.delim("http://www.statsci.org/data/general/twomodes.txt",

header=TRUE)

4. For data stored in ﬁle formats from other software (such as spss, Stata,

and so on), ﬁrst load the package foreign [9], then see library(help=

foreign). Not all functions in the foreign package load the data as data

frames by default (such as read.spss()).

Most data sets used in this book are available in the GLMsData package.

Assuming the GLMsData package is installed, the lungcap data frame used

in Example 1.1 (p. 1) is loaded and used as follows:

> library(GLMsData) # Loads the GLMsData package

> data(lungcap) # Makes the data set lungcap available for use

> names(lungcap) # Shows the names of the variables in lungcap

[1] "Age" "FEV" "Ht" "Gender" "Smoke"

> head(lungcap) # Shows the first six observations

Age FEV Ht Gender Smoke

1 3 1.072 46 F 0

2 4 0.839 48 F 0

3 4 1.102 48 F 0

4 4 1.389 48 F 0

5 4 1.577 49 F 0

6 4 1.418 49 F 0

Appendix A 513

> tail(lungcap) # Shows the last six observations

Age FEV Ht Gender Smoke

649 16 4.070 69.5 M 1

650 16 4.872 72.0 M 1

651 17 3.082 67.0 M 1

652 17 3.406 69.0 M 1

653 18 4.086 67.0 M 1

654 18 4.404 70.5 M 1

> str(lungcap) # Shows the structure of the data frame

'data.frame': 654 obs. of 5 variables:

$Age :int 3444444555...

$ FEV : num 1.072 0.839 1.102 1.389 1.577 ...

$ Ht : num 46 48 48 48 49 49 50 46.5 49 49 ...

$ Gender: Factor w/ 2 levels "F","M": 1111111111...

$ Smoke : int 0000000000...

A summary of the variables in a data frame is produced using summary():

> summary(lungcap) # Summaries of each variable in lungcap

Age FEV Ht Gender

Min. : 3.000 Min. :0.791 Min. :46.00 F:318

1st Qu.: 8.000 1st Qu.:1.981 1st Qu.:57.00 M:336

Median :10.000 Median :2.547 Median :61.50

Mean : 9.931 Mean :2.637 Mean :61.14

3rd Qu.:12.000 3rd Qu.:3.119 3rd Qu.:65.50

Max. :19.000 Max. :5.793 Max. :74.00

Smoke

Min. :0.00000

1st Qu.:0.00000

Median :0.00000

Mean :0.09939

3rd Qu.:0.00000

Max. :1.00000

Notice that the summary() is diﬀerent for numerical and non-numerical vari-

ables.

A.3.7 Working with Data Frames in R

Data loaded from ﬁles (using read.csv() and similar functions) or using

the data() command are loaded as a data frame. A data frame is a set

of variables (numeric, text, or other types) grouped together, as previously

explained. For example, the data frame lungcap contains the data used in

Example 1.1 (p. 1). The data frame contains the variables FEV, Age, Height,

Gender and Smoke, as shown in Sect. A.3.6 in the output from the names()

command.

The data frame lungcap is visible to r, but the individual variables within

this data frame are not visible:

514 Appendix A

> library(GLMsData); data(lungcap)

> Age

Error: object "Age" not found

The objects visible to r are displayed using objects():

> objects()

[1] "lungcap"

To refer to individual variables in the data frame lungcap,use$ between the

data frame name and the variable name, as follows:

> head(lungcap$Age)

[1]344444

This construct can become tedious to use all the time. An alternative is to

use with(), by noting the data frame in which the command should executed:

> with( lungcap, head(Age) )

[1]344444

> with( lungcap, mean(Age) )

[1] 9.931193

> with( lungcap, {

c( mean(Age), sd(Age) )

})

[1] 9.931193 2.953935

> with( lungcap, {

median(Age)

IQR(Age) # Only the last is displayed

})

[1] 4

Another alternative is to attach the data frame so that the individual vari-

ables are visible to r (though this can have unintended side-eﬀects and so

the use of attach() is not recommended):

> attach(lungcap)

> head(Age)

[1]344444

When ﬁnished using the data frame, detach it:

> detach(lungcap)

A.3.8 Using Functions in R

Working with r requires using r functions. r contains a large number of

functions, and the many additional packages add even more functions. Many

r functions have been used already, such as q(), read.table(), seq() and

Appendix A 515

log(). Input arguments to r functions are enclosed in round brackets (paren-

theses), as previously seen. All r functions must be followed by parentheses,

even if they are empty (recall the function q() for quitting r).

Many functions allow several input arguments. Inputs to r functions can

be speciﬁed as positional or named, or even both in the one call. Positional

speciﬁcation means the function reads the inputs in the order in which func-

tion is deﬁned to read them. For example, the r help for the function log()

contains this information in the Usage section:

log(x, base = exp(1))

The help ﬁle indicates that the ﬁrst argument is always the number for which

the logarithm is needed, and the second (if provided) is the base for the

logarithm.

Previously, log() was called with only one input, not two. If input argu-

ments are not given, defaults are used when available. The above extract from

the help ﬁle shows that the default base for the logarithm is e ≈ 2.71828 ...

(that is, exp(1)). In contrast, there is no default value for x. This means

that if log() is called with only one input argument, the result is a natural

logarithm (since base=exp(1) is used by default). To specify a logarithm to

a diﬀerent base, say base 2, a second input argument is needed:

> log(8, 2) # Same as log2(8)

[1] 3

This is an example of specifying the inputs by position. Alternatively, all or

some of the arguments can be named. For example, all these commands are

identical, computing log

> log(x=8, base=2) # All inputs are *named*

[1] 3

> log(8, 2) # Inputs specified by position

[1] 3

> log(base=2, x=8) # Inputs named can be given in any order

[1] 3

> log(8, base=2) # Mixing positional and named inputs

[1] 3

A.3.9 Basic Statistical Functions in R

Basic statistical functions are part of r:

> library(GLMsData); data(lungcap)

> names(lungcap) # The variable names

[1] "Age" "FEV" "Ht" "Gender" "Smoke"

> length( lungcap$Age ) # The number of observations

516 Appendix A

[1] 654

> sum(lungcap$Age) / length(lungcap$Age) # The mean, the long way

[1] 9.931193

> mean( lungcap$Age ) # The mean, the short way

[1] 9.931193

> median( lungcap$Age ) # The median

[1] 10

> sd( lungcap$Age ) # The sample std deviation

[1] 2.953935

> var( lungcap$Age ) # The sample variance

[1] 8.725733

A.3.10 Basic Plotting in R

r has very rich and powerful mechanisms for producing graphics. (In fact,

there are diﬀerent ways to produce graphics, including using the ggplot2

package [14].) Simple plots are easily produced, but very ﬁne control over

many graphical parameters is possible. Consider a simple plot for the fev

data (Fig. A.1, left panel):

> data(lungcap)

> plot( lungcap$FEV ~ lungcap$Age )

The ~ command (~ is called a ‘tilde’) can be read as ‘is described by’. The

variable on the left of the tilde appears on the vertical axis. Equivalent com-

mands to the above plot() command (Fig. A.1, centre panel, p. 517)are:

> plot( FEV ~ Age, data=lungcap )

and

> with( lungcap, plot(FEV ~ Age) )

Notice the axes are labelled diﬀerently. As a general rule, r functions that

use the formula interface (that is, constructs such as FEV ~ Age) allow an

input called data, giving the data frame containing the variables.

The plot() command can also be used without using a formula interface:

> plot( lungcap$Age, lungcap$FEV )

This also produces Fig. A.1 (left panel). Using this approach, the variable

appearing as the second input is plotted on the vertical axis.

Plots can be enhanced in many ways. Compare the result of the following

code (the right panel of Fig. A.1) with the output of the previous code (the

left and centre panels of Fig. A.1):

Appendix A 517

51015

12345

lungcap$Age

lungcap$FEV

51015

Age

FEV

0 5 10 15 20

FEV vs Age

for the lungcap data

Age (years)

FEV (litres)

Females

Males

Fig. A.1 Plots of the fev data. Left panel: a simple plot; centre panel: a simple plot

produced using the data input; right panel: an enhanced plot using some of r’s graphical

parameters (Sect. A.3.10)

> plot( FEV ~ Age, # Plot FEV against Age

data=lungcap, # The data frame to use

las=1, # Ensure both axis labels are horizontal

ylim=c(0, 6), # Sets the limits of the vertical axis

xlim=c(0, 20), # Sets the limits of the horizontal axis

xlab="Age (years)", # The horizontal axis label

ylab="FEV (litres)", # The vertical axis label

main="FEV vs Age\nfor the lungcap data", # The main title

pch=ifelse(Gender=="F", 1, 19) ) # (See below)

> legend("bottomright", pch=c(1, 19), # Add legend

legend=c("Females", "Males") )

Notice that the use of \n in the main title speciﬁes a line break.

The construct pch=ifelse(Gender=="F", 1, 19) needs explanation.

The input pch is used to select the plotting character. For example, pch=1

plots the points with an open circle, and pch=19 plots the points with a

ﬁlled circle. The complete list of plotting characters is shown by typing

example(points). Further, pch="F" (for example) would use an F as the

plotting character. The construct pch=ifelse(Gender=="F", 1, 19) is

interpreted as follows:

• For each observation, determine if Gender has the value "F" (that is, if

the gender is female). Note that the quotes are needed, otherwise r will

look for a variable named F, which is the same as the logical FALSE.Also

recall that == is used to make logical comparisons.

•IfGender does have the value "F", then use pch=1 (an open circle) to

plot the observation.

•IfGender does not have the value "F" (that is, the gender is male), then

use pch=19 (a ﬁlled circle) to plot the observation.

518 Appendix A

An alternative to using ifelse(), which would be useful if three or more

categories were to be plotted, is as follows. Begin by preparing the ‘canvas’

for plotting:

> plot( FEV ~ Age,

type="n", # Sets up the plot, but plots "n"othing

data=lungcap, las=1, ylim=c(1.5, 5),

xlab="Age (years)", ylab="FEV (litres)",

main="FEV vs Age\nfor the lungcap data")

Using type="n" sets up the canvas for plotting, but plots nothing on the plot

itself. Points are then added using points():

> points( FEV~Age, pch=1, subset=(Gender=="F"), data=lungcap )

> points( FEV~Age, pch=19, subset=(Gender=="M"), data=lungcap )

These two commands then add the points in two separate steps. The ﬁrst

call to points() plots the females only (by selecting the data subset subset=

(Gender=="F")), using open circles (deﬁned as pch=1). The second call to

points() plots the males only (subset=(Gender=="M")), using ﬁlled circles

(pch=19). Clearly, further points could be added for any number of groups

using this approach. In a similar way, lines can be added to an existing plot

using lines().

A.3.11 Writing Functions in R

One advantage of r is that functionality is easily extended by writing new

functions. Writing functions is only needed occasionally in this book.

As a simple and trivial example, consider writing a function to covert a

decimal number into a percentage:

> as.percentage <- function(x){

# Args:

# x: The decimal value to be turned into a percentage

# Returns:

# The value of x as a percentage

x * 100

}

(This r code can be typed directly into r.)

This function, called as.percentage, takes one input called x.Ther

instruction inside the brackets

{ and } shows what the function actually

does. The lines beginning with the # are comments and can be omitted, but

make the function easier to understand. This function simply multiplies the

value of x by 100. The function as.percentage canbeusedlikeanyotherr

function:

Appendix A 519

> item.cost <- c(110, 42, 25 )

> item.tax <- c( 10, 4, 2.5)

> as.percentage( item.tax / item.cost )

[1] 9.090909 9.523810 10.000000

In r functions, the value of the last unassigned expression is the value re-

turned by the function. Alternatively, the output can be assigned to a vari-

able:

> out <- as.percentage( item.tax / item.cost ); out

[1] 9.090909 9.523810 10.000000

As a more advanced example, consider adapting the function as.

percentage to return the percentage to a given number of signiﬁcant ﬁgures.

In a text editor (such as Notepad in Windows; TextEdit in Mac OS X; vi or

Emacs in linux), enter:

as.percentage <- function(x, sig.figs=2){

# Args:

# x: The value to be turned into a decimal

# sig.figs: The number of significant figures

# Returns:

# The value of x as a percentage, rounded to the requested number of

# significant figures and the value with a "%" sign added at the end

percent <- signif( x * 100, sig.figs)

percent.withsymbol <- paste( percent, "%", sep="")

return( list(PC=percent, PC.symbol=percent.withsymbol ) )

}

The ﬁrst line

as.percentage <- function(x, sig.figs=2){

deﬁnes the name of the function as as.percentage, and declares that it needs

two inputs: the ﬁrst is called x (with no default value), and the second is called

sig.figs (with a default value of 2). The opening parenthesis

{ declares

where the instructions begin to declare what the function does; obviously,

the ﬁnal closing parenthesis

} shows where the function deﬁnition ends.

The lines that follow starting with # are again comments to aid readability.

The next line computes the percentage rounded to the requested number of

signiﬁcant ﬁgures:

percent <- signif( x * 100, sig.figs)

The next line adds the percentage symbol % after converting the number of

a character:

percent.withsymbol <- paste( percent, "%", sep="")

The ﬁnal line is more cryptic:

return( list(PC=percent, PC.symbol=percent.withsymbol ) )

520 Appendix A

This line determines what values the function will return() when ﬁnished.

This return() command returned two values named PC and PC.withsymbol,

combined together in a list(). When the function returns an answer, one

output variable is called PC, which is assigned the value of percent,and

the second output variable is called PC.symbol, which is assigned the value

of percent.withsymbol. You can copy and paste the function into your r

session, and use it as follows:

> out <- as.percentage( item.tax / item.cost )

> out

$PC

[1] 9.1 9.5 10.0

$PC.symbol

[1] "9.1%" "9.5%" "10%"

> out <- as.percentage( item.tax / item.cost, sig.figs=3 )

> out

$PC

[1] 9.09 9.52 10.00

$PC.symbol

[1] "9.09%" "9.52%" "10%"

Functions in r can be very long and complicated (for example, including

code that detects for bad input such as trying to convert text into a percent-

age, or how to handle missing values). Writing functions are only required

in a few cases in this book, and these functions are relatively simple. For

more information on writing functions in r, see, for example, Venables and

Ripley [13] or Maindonald and Braun [8].

* A.3.12 Matrix Arithmetic in R

r performs matrix arithmetic using some special functions. A matrix is de-

ﬁned using matrix(), where the matrix elements are given with the input

data, the number of rows with nrow or columns with ncol (or both), and op-

tionally whether to ﬁll down columns (the default) or across rows (by setting

byrow=TRUE):

> Amat <- matrix( c(1, 2, -3, -2), ncol=2) # Fills by columns (by default)

> Amat

[,1] [,2]

[1,] 1 -3

[2,] 2 -2

> Bmat <- matrix( c(1, 5, -10, 15, -20, -25), nrow=2, byrow=TRUE) # By row

> Bmat

[,1] [,2] [,3]

[1,] 1 5 -10

[2,] 15 -20 -25

Appendix A 521

Standard matrix operations can be performed:

> dim( Amat ) # The dimensions of matrix Amat

[1]22

> dim( Bmat ) # The dimensions of matrix Bmat

[1]23

> t(Bmat) # The transpose of matrix Bmat

[,1] [,2]

[1,] 1 15

[2,] 5 -20

[3,] -10 -25

> -2 * Bmat # Multiply by scalar

[,1] [,2] [,3]

[1,] -2 -10 20

[2,] -30 40 50

Matrix multiplication of conformable matrices requires the special function

%*% to be used:

> Cmat <- Amat %*% Bmat; Cmat

[,1] [,2] [,3]

[1,] -44 65 65

[2,] -28 50 30

Multiplying non-conformable matrices produces an error:

> Bmat %*% Amat

Error in Bmat %*% Amat : non-conformable arguments

Powers of matrices are produced by repeatedly using %*%:

> Amat^2 # Each *element* of Amat is squared

[,1] [,2]

[1,] 1 9

[2,] 4 4

> Amat %*% Amat # Correct way to compute Amat squared

[,1] [,2]

[1,] -5 3

[2,] -2 -2

The usual multiplication operator * is for multiplication of scalars, not ma-

trices:

> Amat * Bmat # FAILS!!

Error in Amat * Bmat : non-conformable arrays

The * operator can also be used for multiplying the corresponding elements

of matrices of the same size:

> Bmat * Cmat

[,1] [,2] [,3]

[1,] -44 325 -650

[2,] -420 -1000 -750

522 Appendix A

The diagonal elements of matrices are extracted using diag():

> diag(Cmat)

[1] -44 50

> diag(Bmat) # diag() even works for non-square matrices

[1] 1 -20

diag() can also be used to create diagonal matrices:

> diag( c(1, -1, 2) )

[,1] [,2] [,3]

[1,]100

[2,] 0 -1 0

[3,]002

In addition, diag() can be used to create identity matrices easily:

> diag( 3 ) # Creates the 3x3 identity matrix

[,1] [,2] [,3]

[1,]100

[2,]010

[3,]001

To determine if a square matrix is singular or not, compute the determi-

nant using det():

> det(Amat)

[1] 4

> Dmat <- t(Bmat) %*% Bmat; Dmat

[,1] [,2] [,3]

[1,] 226 -295 -385

[2,] -295 425 450

[3,] -385 450 725

> det(Dmat) # Zero to computer precision

[1] -2.193801e-09

Zero determinants indicate singular matrices without inverses. (Near-zero de-

terminants indicate near-singular matrices for which inverses may be diﬃcult

to compute.) The inverse of a non-singular matrix is found using solve():

> Amat.inv <- solve(Amat); Amat.inv

[,1] [,2]

[1,] -0.5 0.75

[2,] -0.5 0.25

> Amat.inv %*% Amat

[,1] [,2]

[1,] 1 0

[2,] 0 1

> solve(Dmat) # Not possible: Dmat is singular

Error in solve.default(Dmat) :

system is computationally singular: reciprocal

condition number = 5.0246e-18

Appendix A 523

The use of solve() to ﬁnd the inverse is related to the use of solve() in

solving matrix equations of the form Ax = b where A is a square matrix,

and x unknown. For example, consider the matrix equation



1 −3







−3



In r:

> bvec <- matrix( c(1, -3), ncol=1); bvec

[,1]

[1,] 1

[2,] -3

> xvec <- solve(Amat, bvec); xvec # Amat plays the role of matrix A

[,1]

[1,] -2.75

[2,] -1.25

To check the solution:

> Amat %*% xvec

[,1]

[1,] 1

[2,] -3

This use of solve() also works if bvec is deﬁned without using matrix().

However, the solution returned by solve() in that case is not a matrix either:

> bvec <- c(1, -3); x.vec <- solve(Amat, bvec); x.vec

[1] -2.75 -1.25

> is.matrix(x.vec) # Determines if x.vec is an R matrix

[1] FALSE

> is.vector(x.vec) # Determines if x.vec is an R vector

[1] TRUE

References

[1] Dalgaard, P.: Introductory Statistics with r, second edn. Springer Sci-

ence and Business Media, New York (2008)

[2] Dunn, P.K.: tweedie: Tweedie exponential family models (2017). URL

https://CRAN.R-project.org/package=tweedie. R package version 2.3.0

[3] Dunn, P.K., Smyth, G.K.: GLMsData: Generalized linear model data

sets (2017). URL https://CRAN.R-project.org/package=GLMsData.R

package version 1.0.0

[4] Fox, J.: The R Commander: A basic statistics graphical user interface

to R. Journal of Statistical Software 14(9), 1–42 (2005)

524 Appendix A

[5] Fox, J.: Using the R Commander: A Point-and-Click Interface for R.

Chapman and Hall/CRC Press, Boca Raton FL (2017)

[6] Fox, J., Bouchet-Valat, M.: Rcmdr: R Commander (2016). URL http://

socserv.socsci.mcmaster.ca/jfox/Misc/Rcmdr/. R package version 2.3.1

[7] Henderson, H.V., Velleman, P.F.: Building multiple regression models

interactively. Biometrics 37(2), 391–411 (1981)

[8] Maindonald, J.H., Braun, J.: Data Analysis and Graphics using R, third

edn. Cambridge University Press, UK (2010)

[9] R Core Team: foreign: Read Data Stored by Minitab, S, SAS, SPSS,

Stata, Systat, Weka, dBase, ... (2017). URL https://CRAN.R-project.

org/package=foreign. R package version 0.8-69

[10] R Core Team: R: A Language and Environment for Statistical Comput-

ing. R Foundation for Statistical Computing, Vienna, Austria (2017).

URL https://www.R-project.org/

[11] Smyth, G.K.: Australasian data and story library (Ozdasl) (2011). URL

http://www.statsci.org/data

[12] Smyth, G.K.: statmod: Statistical Modeling (2017). URL https://

CRAN.R-project.org/package=statmod. R package version 1.4.30. With

contributions from Yifang Hu, Peter Dunn, Belinda Phipson and Yun-

shun Chen.

[13] Venables, W.N., Ripley, B.D.: Modern Applied Statistics with S, fourth

edn. Springer-Verlag, New York (2002)

[14] Wickham, H.: ggplot2: Elegant Graphics for Data Analysis. Springer-

Verlag New York (2009)

Appendix B

The GLMsData package

If you have only pretend data, you can only pretend to

analyze it.

Watkins, Scheaﬀer and Cobb [2,p.x]

Almost all of the data ﬁles used in this book are collated in the r package

GLMsData [1]. This package is available from cran, and is downloaded and

installed like any other r package (Sect. A.2.5). The version of GLMsData

used to prepare this book is 1.0.0. Since the publication of this book, the

contents of the GLMsData package may have been updated.

A list of the 97 data ﬁles in the GLMsData package appear below, with

a brief description. For more details about the GLMsData package in gen-

eral, enter library(help = "GLMsData") at the r prompt, assuming the

GLMsData package is installed. For more information about any individ-

ual data set, say lungcap,enter?lungcap at the r prompt (assuming the

GLMsData package is installed and loaded).

AIS Australian Institute of Sports (AIS) data

ants Ants species richness

apprentice Apprentice migration to Edinburgh

babblers Feeding rates of babblers

belection British election candidates

blocks Blocks stacked by children

boric Dead embryos after exposure to boric acid

breakdown Dialetric breakdown data

bttstudy The South African Birth to Ten (BTT) study

budworm Insecticide doses and tobacco budworm

butterfat Butterfat and dairy cattle

ccancer Canadian cancers

ceo CEO salaries

cervical Deaths from cervical cancer

cheese Tasting cheese

cins Canadian car insurance data

crawl The age at which babies start to crawl

cyclones Cyclones near Australia

danishlc Danish lung cancer

dental Decayed, missing and filled teeth

deposit Insecticides

downs Downs Syndrome cases in British Columbia

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7

525

526 Appendix B

dwomen Depression and children

dyouth Depression in adolescents

earinf Ear infections in swimmers

emeraldaug August monthly rainfall in Emerald

energy Energy expenditure

failures Failures of electronic equipment

feedrates Feeding rates of birds

fineroot The root length density of apple trees

fishfood Food consumption for fish

flathead Tiger flathead from trawls

flowers The average number of meadowfoam flowers

fluoro The time of fluoroscopy and total radiation

galapagos Gal\'apagos Island species data

germ Germination of seeds

germBin Germination of seeds

gestation Gestation time

gforces G-induced loss of consciousness

gopher Clutch sizes of Gopher tortoises

gpsleep Sleep times for guinea pigs

grazing Bird abundance in grazing areas

hcrabs Males attached to female horseshoe crabs

heatcap Heat capacity of hydrobromic acid

humanfat Human age and fatness

janka Janka hardness

kstones Treating kidney stones

lactation Lactation of dairy cows

leafblotch Percentage leaf area of leaf blotch

leukwbc Leukaemia survival times

lime Small-leaved lime trees

lungcap Lung capacity and smoking in youth

mammary Adult mammary stem cells

mandible Mandible length and gestational age

manuka Manuka honey and wound healing

motorins Swedish third-party car insurance

mutagen Mutagenicity assay

mutantfreq Cell mutant frequencies in children

nambeware Nambeware products

nhospital Naval hospital maintenance

nitrogen Soil nitrogen

nminer Noisy miner abundance

paper The tensile strength of paper

perm Permeability of building materials

phosphorus Soil phosphorus

pock Pock counts

poison Survival times of animals

polyps The number of polyps and suldinac

polythene Cosmetic company use of polythene

punting Football punting

quilpie Total July rainfall at Quilpie

ratliver Drugs present in rat livers

rootstock Rootstock data

rrates Oxidation rate of benzene

rtrout Weights of rainbow trout

ruminant Energy in ruminant's diets

Appendix B 527

satiswt Satisfaction with weight in youth

sdrink Soft drink delivery times

seabirds Counts of seabirds

serum Mice surviving doses of antipneumococcus serum

setting Heat evolved by setting cement

sharpener Sharpener data

sheep The daily energy requirements for wethers

shuttles O-rings on the space shuttles

teenconcerns Concerns of teenagers

toothbrush Effectiveness of toothbrushes

toxo Toxoplasmosis and rainfall

triangle Artificial data from triangles

trout The effect of potassium cyanate on trout eggs

turbines Fissures in turbine wheels

urinationD Urination time

urinationL Urethral length

wacancer Cancer in Western Australia

wheatrain Annual rainfall in the NSW wheat belt

windmill Power generation by windmills

wwomen Smoking and survival

yieldden Yield of onions at various densities

References

[1] Dunn, P.K., Smyth, G.K.: GLMsData: Generalized linear model data sets

(2017). URL https://CRAN.R-project.org/package=GLMsData. R pack-

age version 1.0.0

[2] Watkins, A.E., Sheaﬀer, R.L., Cobb, G.W.: Statistics in Action, second

edn. Key Curriculum Press (2008)

Selected Solutions

Research has shown that it is eﬀective to combine

example study and problem solving in the initial

acquisition of cognitive skills.

Renkl [3, p. 293]

The data used generally come from the GLMsData [2] package. We do not

explicitly load this package each time it is needed.

> library(GLMsData)

Solutions to Problems from Chap. 1

1.1 The more complex quartic model is similar to the cubic. The cubic is possibly

superior to the quadratic, so we probably prefer the cubic.

1.4 The proportion testing positive is between zero and one. The cubic regression

model is not good—it permits proportions outside the physical range; the cubic glm is

preferred.

1.5 1. Linear in the parameters; suitable for linear regression and glms. 2. Not linear in

parameters. 3. Linear in the parameters; suitable for glms. 4. Linear in the parameters;

suitable for glms.

1.6

> data(turbines)

> ### Part 1

> names(turbines)

> ### Part 4

> summary(turbines)

> ### Part 5

> plot(Fissures/Turbines ~ Hours, data=turbines, las=1)

2. All variables are quantitative. 3. Clearly the number of hours run is important for

knowing the proportion of ﬁssures. The proportion must be between 0 and 1 obviously.

1.9

> data(blocks); blocks$Trial <- factor(blocks$Trial)

> blocks$cutAge <- cut(blocks$Age, breaks=c(0, median(blocks$Age), Inf))

> ### Part 1

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7

529

530 Selected Solutions

> summary(blocks)

> ### Part 2

> par( mfrow=c(2, 4))

> plot( Time~Shape, data=blocks, las=1)

> plot( Time~Trial, data=blocks, las=1)

> plot( Time~Age, data=blocks, las=1)

> with(blocks, interaction.plot(Shape, cutAge, Time))

> ### Part 4

> plot( Number~Shape, data=blocks, las=1)

> plot( Number~Trial, data=blocks, las=1)

> plot( Number~Age, data=blocks, las=1)

> with(blocks, interaction.plot(Shape, cutAge, Number))

3. For both responses: shape seems important; trial number doesn’t; age possibly. 5. Per-

haps interactions.

Solutions to Problems from Chap. 2

2.1 1. β

is the predicted value when x =0.2. α

is the predicted value when x is

equal to the mean of x (that is,

x). The second form may allow a better interpretation

of the constant, since x = 0 may be far from the values of x used to ﬁt the model.

2.2 Solve the equations. Note that



− ¯x

)



−









and



−¯x



−



¯y

, which makes the connection to the given

formula a bit easier to see.

2.4 1. Expand S =(y − Xβ)

W(y − Xβ) to get the result. 2. Diﬀerentiating with

respect to β gives ∂S/∂β = −2X

Wy +2X

WXβ. 3. Setting the diﬀerential to zero

and solving gives X

WXβ. Pre-multiplying by (X

WX)

−1

gives the result.

2.6 E[

β]=(X

WX)

−1

WE[y]=(X

WX)

−1

W(Xβ)=β.

2.8 Substituting for R

on the right in terms of ss gives {ssReg/(p



−1)}/{sst/(n−p



)},

which is F .

2.9 1. A:



11111

11−1 −10



;B:



11111

111−1 −1



;C:



1111 1

10.50−0.5 −1



2. Then, use that var[ˆμ]=x

−1

with x

=[1 x] to obtain var[ˆμ

]=(1/4)

/5; var[ˆμ

]=(5− 6x +5x

)/16; var[ˆμ

]=(1− 2x

)/5.

> x <- seq(-1, 1, length=100)

> xA <- c(1, 1, -1, -1, 0)

> xB <- c(1, 1, 1, 1, -1)

> xC <- c(1, 0.5, 0, -0.5, -1)

> varA <- function(x){0.25 + x^2/5}

> varB <- function(x){(5 - 6*x + 5*x^2)/16}

> varC <- function(x){(1+2*x^2)/5}

> vA <- varA(x); vB <- varB(x); vC <- varC(x)

> plot( range(c(vA, vB, vC)) ~ range(x), type="n", ylim=c(0, 1.2),

ylab="Var. of predictions", xlab="x values", las=1)

> lines(varA(x) ~ x, lty=1, lwd=2)

> lines(varB(x) ~ x, lty=2, lwd=2)

Selected Solutions 531

> lines(varC(x) ~ x, lty=3, lwd=2)

> legend("top", lwd=2, lty=1:3, legend=c("Design A", "Design B",

"Design C"))

As would be expected from the location of the x values: A produces the most uni-

form small prediction errors; B produces smaller prediction errors for larger x values; C

produces smaller prediction errors in the middle of the range of x values.

2.10 1. The Taylor series expansion is f(x)=f(¯x)+df/dx(x−¯x)+d

f/dx

(x−¯x)

/2+

···. 2. f(x) is linear in x,ifx − ¯x is small. 3. Any function can be considered locally

approximately linear.

2.15 2. The relationship between the number of ﬂowers per plant and light intensity

has diﬀerent intercepts for the diﬀerent timings, but the same slope. 3. The relationship

between the number of ﬂowers per plant and light intensity has diﬀerent intercepts and

diﬀerent slopes for the diﬀerent timings. 4. Interaction term doesn’t seem necessary.

5. Makes no diﬀerence to the parameter estimates or standard errors. However, the

estimate of σ is diﬀerent. 6. The interaction term does not seem needed.

> data(flowers)

> wts <- rep(10, length(flowers$Light) )

> ### Part 1

> plot(Flowers~Light, data=flowers, pch=ifelse(Timing=="PFI", 1, 19))

> legend("topright", pch=c(1, 19), legend=c("PFI","Before PFI"))

> ### Part 3

> m1 <- lm(Flowers~Light*Timing, data=flowers, weights=wts); anova(m1)

> m2 <- lm(Flowers~Light+Timing, data=flowers, weights=wts); anova(m2)

> ### Part 5

> m1.nw <- lm(Flowers~Light*Timing, data=flowers); anova(m1.nw)

> m2.nw <- lm(Flowers~Light+Timing, data=flowers); anova(m2.nw)

> summary(m1); summary(m1.nw)

> ### Part 6

> abline(coef(m2)[1], coef(m2)[2], lty=1)

> abline(sum(coef(m2)[c(1, 3)]), coef(m2)[2], lty=2)

2.18

> data(blocks)

> ### Part 5

> m0 <- lm( Time ~ Shape, data=blocks); anova( m0 )

> mA <- lm( Time ~ Trial + Age + Shape, data=blocks); anova( mA )

> ### Part 6

> mB <- update(mA, . ~ Trial + Age*Shape); anova( mB )

> t.test(Time~Shape, data=blocks)

> summary(m0)

> ### Part 7

> m1 <- lm( Time~Shape, data=blocks); anova(m1)

1. Possible increasing variance. Perhaps non-linear? 2. The relationship between age

and time has diﬀerent intercepts and slopes for the two shapes. 3. Time depends on age

and trial number, and the eﬀect of age depends on the trial number. 4. Time depends

on age and shape, and both depend on the trial number. 8. On average, the time taken

to stack cylinders is 14.45slessthanforcubes.

532 Selected Solutions

Solutions to Problems from Chap. 3

3.2 Expand the expressions, simplify, and the results follow.

3.8

> data(lungcap)

> ### Part 1

> m1 <- lm(FEV~factor(Smoke), data=lungcap)

> ### Part 2

> m2 <- lm(FEV~factor(Smoke)+Age+Ht+factor(Gender), data=lungcap)

> ### Part 3

> m3 <- lm(log(FEV)~factor(Smoke)+Age+Ht+factor(Gender), data=lungcap)

> ### Part 4

> summary(m1); summary(m2); summary(m3); anova(m3) # Prefer m3

1. Smokers have a larger fev by an average of 0.7107 L. 2. Smokers have a smaller fev

by an average of −0.08725 L. 3. Smokers have a smaller fev by, on average, a factor of

0.9165.

3.10

> data(cheese)

> m4 <- lm( log(Taste) ~ log(H2S) + Lactic + Acetic, data=cheese )

> scatter.smooth( rstandard(m4) ~ fitted(m4) )

> qqnorm( rstandard(m4) ); qqline( rstandard(m4) )

> plot( cooks.distance(m4), type="h")

3.11

> data(fishfood); par(mfrow=c(2, 3))

> ### Part 1

> m1 <- lm( log(FoodCon) ~ log(MaxWt) + log(Temp) + log(AR) + Food,

data=fishfood); anova(m1)

> ### Part 2

> plot(rstandard(m1)~fitted(m1)); qqnorm(rstandard(m1))

> plot( cooks.distance(m1), type="h") # Model looks OK

> m2 <- update(m1, . ~ log(MaxWt) * log(Temp) * Food * log(AR))

> m3 <- step(m2); anova(m1, m3) # Model m3 a bit better

> plot(rstandard(m3)~fitted(m3)); qqnorm(rstandard(m3))

> plot( cooks.distance(m3), type="h") # Model looks OK

3. Unravelling, the model has the form ˆμ =exp(β

···. 4. The interaction model

is slightly better if the automated procedure can be trusted, by the ANOVA test (and

AIC).

3.13

> data(flowers)

> m1 <- lm(Flowers~Light+Timing, data=flowers)

> ### Part 1

> scatter.smooth( rstandard(m1) ~ fitted(m1) )

> qqnorm( rstandard(m1) ); qqline( rstandard(m1) )

> plot( cooks.distance(m1), type="h")

> plot( rstandard(m1) ~ flowers$Light)

> ### Part 2

> rowSums(influence.measures(m1)$is.inf)

Selected Solutions 533

2. No observations reported as inﬂuential.

3.16

> data(blocks); par(mfrow=c(2, 4))

> m1 <- lm( Time~Shape, data=blocks); anova(m1)

> ### Part 1

> plot( rstandard(m1) ~ fitted(m1) )

> qqnorm( rstandard(m1) ); qqline( rstandard(m1) )

> plot( cooks.distance(m1), type="h")

> plot( rstandard(m1) ~ blocks$Shape)

> rowSums(influence.measures(m1)$is.inf)

> ### Part 2

> m2 <- lm( log(Time)~Shape*Age, data=blocks); anova(m2)

> m2 <- update(m2, .~Shape+Age); anova(m2)

> m2 <- update(m2, .~Shape); anova(m2)

> plot( rstandard(m2) ~ fitted(m2) )

> qqnorm( rstandard(m2) ); qqline( rstandard(m2) )

> plot( cooks.distance(m2), type="h")

> plot( rstandard(m2) ~ blocks$Shape)

> rowSums(influence.measures(m2)$is.inf)

1. The model includes only Shape. The Q–Q plot shows non-normality; the variance is

diﬀerent between cubes and cylinders. Perhaps inﬂuential observations. 2. The model

diagnostics appear better, if not perfect, after applying a log-transform.

3.21

> data(paper)

> ### Part 1

> plot( Strength~Hardwood, data=paper)

> ### Part 2

> m1 <- lm(Strength ~ poly(Hardwood, 5), data=paper); summary(m1)

> ### Part 3

> m2 <- lm(Strength ~ ns(Hardwood, df=7), data=paper); summary(m2)

> ### Part 4

> newH <- seq( min(paper$Hardwood), max(paper$Hardwood), length=100)

> newy1 <- predict( m1, newdata=data.frame(Hardwood=newH))

> newy2 <- predict( m2, newdata=data.frame(Hardwood=newH))

> lines(newy1~newH)

> lines(newy2~newH, lty=2)

3.23

> data(gopher)

> ### Part 1

> par( mfrow=c(2, 2))

> plot( ClutchSize ~ Temp, data=gopher)

> plot( ClutchSize ~ Evap, data=gopher)

> ### Part 3

> gt.lm <- lm( ClutchSize ~ Temp + Evap, weights=SampleSize, data=gopher)

> summary(gt.lm)

> ### Part 4

> anova(gt.lm)

> ### Part 5

> cor(cbind(gopher$ClutchSize, gopher$Temp, gopher$Evap, gopher$Latitude))

534 Selected Solutions

> ### Part 6

> plot( Evap ~ Latitude, data=gopher)

> plot( Temp ~ Latitude, data=gopher)

> m1 <- lm(ClutchSize~Evap, data=gopher)

> par(mfrow=c(2, 2))

> plot( rstandard(m1) ~ gopher$Latitude)

> plot( rstandard(m1) ~ fitted(m1))

> plot(cooks.distance(m1), type="h")

> qqnorm( rstandard(m1)); qqline( rstandard(m1))

1. Some reasonable positive relationships. 2. Each site has a diﬀerent number of

clutches. 3. No signiﬁcant explanatory variables. 4. No signiﬁcant explanatory variables.

6. Evaporation and temperature look related to latitude.

3.25

> data(ratliver)

> ### Part 1

> plot( DoseInLiver ~ BodyWt, data=ratliver)

> plot( DoseInLiver ~ LiverWt, data=ratliver)

> plot( DoseInLiver ~ Dose, data=ratliver)

> ### Part 2

> m1 <- lm(DoseInLiver ~ BodyWt + LiverWt + Dose, data=ratliver)

> ### Part 3

> summary(m1); anova(m1)

> ### Part 4

> influence.measures(m1)

> infl <- which.max(cooks.distance(m1))

> ### Plot 5

> plot(BodyWt ~ Dose, data=ratliver)

> points(BodyWt ~ Dose, subset=(infl), pch=19, data=ratliver)

> ### Plot 6

> m2 <- update(m1, subset=(-infl) ); summary(m2); anova(m2)

1. Possible relationships.

Solutions to Problems from Chap. 4

4.2 Apply the derivatives and the results follow.

4.5

1. For one observation:  = −log μ − y/μ.

2. U(μ)=−n/μ +



/μ

= n(ˆμ −μ)/μ

3. ˆμ =



/n.

4. J(μ)=(−nμ +2



)/μ

= −n(μ − 2ˆμ)/μ

; I(μ)=n/μ

5. se(ˆμ)=I(ˆμ)

−1/2

= μ/

√

6. W = n(ˆμ − 1)

/ˆμ

7. S = n(ˆμ − 1)

8. L =2n(ˆμ − log ˆμ − 1).

10. W, S and L are similar near ˆμ, but dissimilar far away from ˆμ. For larger values of

n, the curves are sharper at ˆμ, so there is more information.

Selected Solutions 535

> par(mfrow=c(1, 2))

> muhat <- seq(0.5, 2, length=200)

> ### Part 9

>n<-10

> W <- (muhat-1)^2/(muhat^2/n)

> S <- n*(muhat-1)^2

> L <- 2*n*(muhat-log(muhat)-1)

> plot(range(W)~range(muhat), type="n", main="n = 10", xlab="x", ylab="")

> lines(W~muhat)

> lines(S~muhat, lty=2)

> lines(L~muhat, lty=3)

> legend("top", lty=1:3, legend=c("Wald","Score","LRT"))

> abline(v=1, lty=4)

> ### Part 10

>n<-100

> W <- (muhat-1)^2/(muhat^2/n)

> S <- n*(muhat-1)^2

> L <- 2*n*(muhat-log(muhat)-1)

> plot(range(W)~range(muhat), type="n", main="n = 100", xlab="x", ylab="")

> lines(W~muhat)

> lines(S~muhat, lty=2)

> lines(L~muhat, lty=3)

> legend("top", lty=1:3, legend=c("Wald","Score","LRT"))

> abline(v=1, lty=4)

4.6

> set.seed(252627)

> n <- 200; yy <- rexp(n, 1); len.mu <- 250

> #Part 1:

> muhat.vec <- seq(0.75, 1.25, length=len.mu)

> llh <- array(dim=len.mu)

> for (i in (1:length(muhat.vec))){

llh[i] <- sum( log( dexp(yy, rate=1/muhat.vec[i]) ) )

}

> plot(llh~muhat.vec, type="l", lwd=2, las=1, xlab="mu")

> muhat <- mean(yy); critical <- qchisq(1-0.05, df=1)

> abline(v=1); abline(v=muhat); abline(h=max(llh)- critical, lty=2)

> # Part 2:

> W <- (muhat-1)^2/(muhat^2/n); S <- n * (muhat-1)^2

> L <- 2*n*(muhat - log(muhat)-1)

> c(W, S, L); pexp( c(W, S, L), rate=1, lower.tail=FALSE)

> # Part 3:

> W <- (muhat.vec-1)^2/(muhat.vec^2/n); S <- n * (muhat.vec-1)^2

> L <- 2*n*(muhat.vec - log(muhat.vec)-1)

> plot(W~muhat.vec, type="l", lwd=2, ylab="Test statistic", xlab="mu hat")

> lines(S~muhat.vec, lty=2, lwd=2); lines(L~muhat.vec, lty=3, lwd=2)

> abline(v=1); abline(v=muhat); abline(h=critical)

> legend("top", lty=1:3, legend=c("Wald","Score","L. Ratio"),

lwd=2, bg="white")

> # Parts 4 and 5

> se <- sqrt(muhat/n); se; c(muhat - se*1.960, muhat+se*1.960)

536 Selected Solutions

Solutions to Problems from Chap. 5

5.1 2. Geometric: θ =log(1− p); κ(θ)=log{(1 −p)/p}; φ =1.5. Strict arcsine:

θ =logp; κ(θ)=arcsinp; φ =1.

5.4 Apply the formula.

5.7 K



(t)=φκ



(θ + tφ); on setting t = 0 the results follow.

5.13 τ =1× y/(y − 0)

=(1/y) ≤ (1/3).

5.16

1. Proceed:

(t)=

∞



y=0

exp(−λ)λ

/y! × e

=exp(−λ)

∞



y=0

{λ exp t}

/y!=exp(−λ + λe

2. K

(t)=logM

(t)=−λ + λe

3. Diﬀerentiating and setting t = 0 gives the required results.

5.17 1. M

¯y

(t)=E[exp{t(y

+ ···y

)/n}]=E[exp(ty/n)]

= M

(t/n)

since the y

are

iid. 2. Then, K

¯y

(t)=logM

¯y

(t)=n log M

(t/n)=nK

(t/n)=n{κ(θ + tφ/n) −κ(θ)}/

φ. 3. This is the cgf of edm(μ, φ/n).

5.18

1. Follow Sect. 5.3.6 (p. 217): θ =arctanμ; κ(θ)=−log(cos θ)={log(1 + μ

)}/2.

2. d(y,μ)=2[y(arctan y − arctan μ) − (1/2) log{(1 + y

)/(1 + μ

)}].

3. The saddlepoint approximation:

P(y; μ, φ)=1/



2πφ(1 + y

)exp{−d(y, μ)/(2φ)}.

4. Saddlepoint approx. expected to be OK if φ(1 + y

)/y

≤ 1/3; or y

≥−3/2when

φ =1,ory

≥−3whenφ =0.5. These expressions are true for all y.

5. The canonical link function has η = θ,whichisη =arctanμ.

> y <- seq(-4, 2, length=200); phi<-0.5; phi2 <- 1; mu <- -1

> b <- 1/sqrt(2*pi*phi*(1+y^2)); b2 <- 1/sqrt(2*pi*phi2*(1+y^2))

> dev <- 2*(y*(atan(y) - atan(mu))-(1/2)*log((1+y^2)/(1+mu^2)))

> plot( b * exp(-dev/(2*phi ))~y, type="l")

> lines( b2* exp(-dev/(2*phi2))~y, lty=2)

> legend("topright", lty=1:2, legend=c("phi=0.5","phi=1"))

5.22 M

(t)=

∞

exp(ty)exp(−y) dy =1/(1 − t), provided t<1 (otherwise the limit

as y →∞is not deﬁned). Taking logs, K

(t)=logM

(t)=−log(1 −t), provided t<1.

Diﬀerentiating, K



(t)=(1− t)

−1

,soK



(0) = 1. Likewise for the variance.

5.24 g(μ)=|μ| is not valid (not diﬀerentiable when −∞ <μ<∞). g(μ)=μ

is not

valid when −∞ <μ<∞ (not a monotonic function).

5.25

> data(blocks)

> ### Part 1

> par(mfrow=c(1, 2))

> plot(jitter(Number)~Age, data=blocks)

> plot( Number~cut(Age, 3), data=blocks)

Responses are counts; variance increases with mean. Poisson glm?

Selected Solutions 537

Solutions to Problems from Chap. 6

6.3 Consider w

− μ

)

/V (μ)

. Here, μ is constant, then taking expected values

/V (μ)

E[(y

− μ

)

]. By deﬁnition, the expected value of (y

− μ

)

is var[y]=

φV (μ)/w

, so the expression simpliﬁes to φ. Thus the expected value of the Pearson

estimator is 1/(n − p



) ×



i=1

φ = {n/(n − p



)}φ with p



estimated regression pa-

rameters, approximately unbiased. With μ known and hence no unknown regression

parameters, p



= 0 and then the expected value is φ, so the estimate is unbiased.

6.6

1. Using

∂

∂β

∂U(β

)

∂μ

∂β

. The ﬁrst derivative comes from Problem 6.5.For

the second, using that the canonical link function is g(μ)=η =log{μ/(1 −μ)},we

getthatdη/dμ =1/{μ(1 − μ)} and ∂μ/∂β

= μ(1 − μ)x

. Combining,

= −

∂

∂β



i=1

(1 − μ

2. z =log{μ/(1 − μ)} +(y − μ)/{μ(1 − μ)}.

6.9

1. Using η =logμ,thendη/dμ =1/μ.HenceW

= w

/μ

and U



i=1

−

/(φμ

2. z

=logμ

+(y

− μ

)/μ

3. Finding  and diﬀerentiating with respect to φ leads to

φ = D(y,μ)/n.

φ = D(y,μ)/(n − p



φ = X

/(n − p



) where X



i=1

− ˆμ

)

/ˆμ

6.10

> data(blocks)

> m1 <- glm(Number~Age, data=blocks, family=poisson)

> m1; deviance(m1); summary(m1)

Solutions to Problems from Chap. 7

7.1

> ### Part 1

> L <- c(0.602, 14.83, 2.83)

> p.LRT <- pchisq(L, df=1, lower.tail=FALSE)

> ### Part 2

> beta <- c(0.143, 1.247, -0.706)

> se <- c(0.19, 0.45, 0.45)

> Wald <- beta/se

> p.Wald <- pnorm(abs(Wald), lower.tail=FALSE)*2

> cbind(p.LRT, p.Wald)

> ### Part 4

> zstar <- qnorm(0.975)

> margin.err <- zstar*0.45

> c( 1.247 - margin.err, 1.247, 1.247 + margin.err)

538 Selected Solutions

7.3

> ### Part 1

> ppois( 7, 1.8) # Small probably of exceeding seven

> ppois( 7, 2.5) # Small probably of exceeding seven

> ### Part 2

> beta <- c(0.23, 0.04, 0.06, 0.01, 0.09, 0.05, 0.30)

> se <- c(0.13, 0.04, 0.05, 0.03, 0.06, 0.02, 0.07)

> z <- beta/se; pvals <- (1-pnorm(abs(z)))*2

> round(pvals, 3)

1. The counts have an upper limit: weeks have a maximum of seven days. However,

the means are relatively small, so a Poisson glm may be OK.

2. Wald test: z =0.30/0.07 ≈ 4.3, which is highly signiﬁcant. There is evidence of a

diﬀerence.

3. Junior Irish legislators spend an average of 0.3 more days per week in their con-

stituency.

4. 0.30 ± 1.960 × 0.07.

5. ‘Geographic proximity’ and ‘Nation’ are statistically signiﬁcant.

6. The systematic component:

log μ =0.23 + 0.04x

+0.06x

+0.01x

+0.09x

+0.05x

+0.30x

;

the random component: y

∼ Pois(μ

7.4

> data(blocks); library(statmod)

> m1 <- glm(Number~Age, data=blocks, family=poisson)

> m0 <- update(m1, .~1)

> ### Part 1

> z.Wald <- coef(summary(m1))[2, 3]

> P.Wald <- coef(summary(m1))[2, 4]

> ### Part 2

> z.score <- glm.scoretest(m0, blocks$Age)

> P.score <- 2*(1-pt(abs(z.score), df=df.residual(m1)))

> ### Part 3

> chisq.LRT <- anova(m1)[2, 2]

> P.LRT <- anova(m1, test="Chisq")[2, 5]

> # Part 4

> round(c(z.Wald, z.score, sqrt(chisq.LRT)), 4)

> round(c(P.Wald, P.score, P.LRT), 4); min(blocks$Number)

> ### Part 8

> newA <- seq( min(blocks$Age), max(blocks$Age), length=100)

> newB <- predict( m1, newdata=data.frame(Age=newA), type="response",

se.fit=TRUE)

> plot( jitter(Number)~Age, data=blocks)

> lines(newB$fit ~ newA, lwd=2)

> t.star <- qt(p=0.975, df=df.residual(m1))

> ci.lo <- newB$fit - t.star * newB$se.fit

> ci.hi <- newB$fit + t.star * newB$se.fit

> lines(ci.lo~newA, lty=2)

> lines(ci.hi~newA, lty=2)

5. For a Poisson glm, expect the saddlepoint approximation to be suﬃcient if the

smallest y ≥ 3; here the minimum is 3, so expect the saddlepoint approximation to be

Selected Solutions 539

OK. 6. For a Poisson glm, expect the CLT approximation to be suﬃcient if the smallest

y ≥ 5; here the minimum is 3 (and there are ten counts of 4), so the CLT approximation

may be insuﬃciently accurate.

Solutions to Problems from Chap. 8

8.3 r

=sign(y

−μ

)



2[y log(y/μ)+(1− y)log{(1 − y)(1 − μ)}]. The result follows

from substituting y =0andy = 1, and using that lim

t→0

t log t =0.

8.7 1. r

=(y − μ)/μ =(y/μ) − 1. r



−log(y/μ)+(y − μ)/μ.Since

F(y; μ)=1−exp(−y/μ), r

= Φ

−1

[1 − exp(−y/μ)]. Hence r

= −0.571; r

= −0.552;

= Φ

−1

(0.34856) = −0.389. 2. Then r

=0;r

= Φ

−1

(0.632) = 0.337.

= 0 even though y = μ. 3. While quantile residual have a normal distribution, they

do not necessarily report a zero residual when y = μ. (They are best used for identifying

patterns.)

8.11

> data(blocks); library(statmod)

> m1 <- glm(Number~Age, data=blocks, family=poisson)

> par(mfrow=c(2, 2))

> plot( rstandard(m1)~fitted(m1))

> plot(cooks.distance(m1), type="h")

> qqnorm(rstandard(m1)); qqnorm(qresid(m1))

> colSums(influence.measures(m1)$is.inf)

8.13

> data(triangle)

> ### Part 2

> m1 <- glm( y~I(x1^2) + I(x2^2), data=triangle,

family=quasi(link=power(lambda=2), variance="constant"))

> m2 <- glm( y~I(x1^2) + I(x2^2), data=triangle,

family=quasi(link=power(lambda=2), variance="mu^2"))

> plot( rstandard(m1)~fitted(m1)); qqnorm(rstandard(m1))

> plot(cooks.distance(m1), type="h")

> plot( rstandard(m2)~fitted(m2)); qqnorm(rstandard(m2))

> plot(cooks.distance(m2), type="h")

> colSums(influence.measures(m1)$is.inf)

> colSums(influence.measures(m2)$is.inf)

1. μ

= x

+ x

so that the link function is g(μ)=μ

Solutions to Problems from Chap. 9

9.1 The Taylor series expansion: sin

−1

√

y =sin

−1

√

μ +(y −μ)/



(1 − μ)μ

+ ···.

On computing the variance, var[sin

−1

√

y] ≈ var[y]/{4(1 − μ)μ}, which is equivalent to

var[y] being a constant times (1 − μ)μ, the binomial variance function.

540 Selected Solutions

9.5

> ### Part 2

> beta <- c(-6.949, 0.805, 0.161, 0.332, 0.116)

> se <- c(0.377, 0.0444, 0.113, 0.0393, 0.0204)

> z <- beta/se

> ### Part 3

> ci <- cbind( beta-1.96*se, beta+1.96*se)

> pvals <- (1-pnorm(abs(z)))*2; OddsRatio <- exp(beta)

> round( cbind(beta, se, z, ci, pvals, OddsRatio), 3)

1. log{μ/(1 − μ)} = −6.949 + 0.805x

+0.161x

+0.332x

+0.116x

,withthex

deﬁned in the problem. 4. For example, the odds of having an apnoea-hyponoea index

of 1 is 1.123 greater than the odds that the index is 0, after adjusting for the other

variables.

9.7

> library(statmod)

> data(shuttles)

> ### Part 1

> plot( Damaged/6 ~ Temp, data=shuttles)

> ### Part 2

> shuttle.m <- glm(Damaged/6 ~ Temp, weights=rep(6, length(Temp)),

family=binomial, data=shuttles)

> ### Part 3

> qqnorm( qresid(shuttle.m))

> colSums(influence.measures(shuttle.m)$is.inf)

> ### Part 4

> predict(shuttle.m, newdata=data.frame(Temp=31), type="response")

5. The temperature at which 50% of the O-rings fail. Since we do not want O-rings to

fail, probably a higher threshold would be more useful.

9.9

> library(MASS); data(budworm)

> ### Part 1

> budworm$Prop.Killed <- budworm$Killed/budworm$Number

> plot( Prop.Killed ~ log2(Dose),

pch=ifelse(Gender=="F", 1, 19), data=budworm)

> ### Part 2

> m1.logit <- glm( Prop.Killed ~ Gender * log2(Dose)-1, weights=Number,

family=binomial(link=logit), data=budworm )

> anova(m1.logit, test="Chisq")

> m1.logit <- glm( Prop.Killed ~ Gender + log2(Dose)-1, weights=Number,

family=binomial(link=logit), data=budworm )

> ### Part 3

> newD <- seq( min(budworm$Dose), max(budworm$Dose), length=100)

> newP.F <- predict( m1.logit, newdata=data.frame(Dose=newD, Gender="F"),

type="response" )

> newP.M <- predict( m1.logit, newdata=data.frame(Dose=newD, Gender="M"),

type="response" )

> lines( newP.F ~ log2(newD), lty=1)

> lines( newP.M ~ log2(newD), lty=2)

> legend("topleft", lty=1:2, legend=c("Females", "Males"))

> ### Part 4 and 5

Selected Solutions 541

> summary(m1.logit)

> ### Part 6

> LD50.F <- dose.p(m1.logit, c(1, 3)); LD50.M <- dose.p(m1.logit, c(2, 3))

> exp(c(LD50.F, LD50.M))

> ### Part 7

> confint( m1.logit, level=.90)

3. Model for males looks better than model for females.

9.11

> li <- factor( c(0, 0, 0, 0, 1, 1, 1, 1), labels=c("Absent", "Present") )

> m <- c(3, 2, 4, 1, 5, 5, 9, 17); y <- c(3, 2, 4, 1, 5, 3, 5, 6)

> gender <- gl(2, 2, 8, labels=c("Female", "Male"))

> par( mfrow=c(1, 3))

> ### Part 1

> plot(y/m~li); plot(y/m~gender)

> interaction.plot(li, gender, y/m)

> ### Part 2

> m1 <- glm( y/m ~ gender, weights=m, family=binomial)

> m2 <- glm( y/m ~ li+gender, weights=m, family=binomial)

> m3 <- glm( y/m ~ gender+li, weights=m, family=binomial)

> summary(m2)

> ### Part 3

> anova(m2, test="Chisq"); anova(m3, test="Chisq")

> ### Part 4

> z.score <- glm.scoretest(m1, as.numeric(li))

> p.score <- 2*(1-pnorm(abs(z.score)))

> c(z.score, p.score)

5. Wald test results show nothing greatly signiﬁcant; the others do. The Hauck–Donner

eﬀect, since y/m is always 1 when li is Absent.

Solutions to Problems from Chap. 10

10.1

1. θ =log{μ/(μ + k)}; κ(θ)=k log(μ + k).

2. The mean is dκ/dθ =dκ/dμ × dμ/dθ;hencedθ/dμ = k/{μ(μ + k)}. Expanding,

the mean is μ (as expected). Variance:

κ/dθ

=d/dθ(dκ/dθ)=d/dμ(dμ/dθ)dκ/dθ = μ(μ + k)/k,

as to be shown.

3. The canonical link is η =log{μ/(μ + k)}.

10.3

1. θ =logλ and κ(θ)=λ +log{1 − exp(−λ)}.

2. dθ/dλ =1/λ;dκ(θ)/dλ =1/{1 − exp(−λ)}, and the result follows.

3. var[y]=V (μ)=λ{1 − exp(−λ

) − λ exp(−λ)}/{1 − exp(−λ)}

542 Selected Solutions

> ### Part 4

> y <- 1:10; lambda <- 2

> p <- exp(-lambda) * lambda^y / ( (1-exp(-lambda)) * factorial(y) )

> plot(p~y, type="h", xlim=c(0, 10), xlab="Prob.", las=1, main="lambda=2")

> y1 <- 0:10; p1 <- dpois(y, lambda=lambda)

> points(p1~y, pch=19)

> legend("topright", pch=c(NA, 19), lty=c(1, NA),

legend=c("Truncated", "Standard"))

10.9

> data(danishlc)

> danishlc$Rate <- danishlc$Cases / danishlc$Pop * 1000 # Rate per 1000

> danishlc$Age <- ordered(danishlc$Age, # Preserve age-order

levels=c("40-54", "55-59", "60-64", "65-69", "70-74", ">74") )

> danishlc$City <- abbreviate(danishlc$City, 1)

> ### Part 1

> dlc.bin <- glm( cbind(Cases, Pop-Cases) ~ Age,

family=binomial, data=danishlc)

> dlc.psn <- glm( Cases ~ offset( log(Pop) ) + Age,

family=poisson, data=danishlc)

The binomial and Poisson models give nearly identical results:

> data.frame( coef(dlc.bin), coef( dlc.psn))

> c( Df=df.residual(dlc.bin),

Dev.Bin=deviance(dlc.bin),

Dev.Poisson=deviance(dlc.psn) )

The conditions are satisﬁed, so the binomial and Poisson models are equivalent:

> max( fitted( dlc.bin) ) ### Small pi

> min( danishlc$Pop ) ### Large m

10.4 1. The number of politicians switching parties is a count. 2. In non-election years,

exp(1.051) = 2.86 times more politicians switch on average. 3. z =1.051/0.320 = 3.28,

and so P =0.00026. 4. Use z =1.645 and then 1.051±(1.645×0.320), or 1.051±0.5264.

10.6

> ### Part 2

> ResDev <- c(732.74, 662.25, 649.01, 637.22)

> Dev <- abs(diff(ResDev))

> p.lrt <- round( pchisq(Dev, df=1, lower.tail=FALSE), 3)

> ### Part 3

> beta <- c(0.238, 0.017,-0.028)

> se <- c(0.028, 0.035, 0.009)

> z <- beta/se

> p.wald <- round( 2*(1 - pnorm( abs(z) ) ), 3)

> ### Part 5

> cbind(p.lrt, p.wald); pchisq(ResDev[4], df=614, lower.tail=FALSE)

1. log ˆμ = −2.928+0.238C+0.017M−0.028M

. 5. The residual deviance (637.22) is only

slightly larger than the residual df (614). 6. and 7. Write η = β

+ β

C + β

M + β

;

solving shows the maximum occurs at M = −β

/(2β

)=0.15. This is small (and

far less than the minimum possible manipulation of one whole egg), suggesting that

Selected Solutions 543

manipulating the clutch-size in any way will reduce the number of oﬀspring surviving,

supporting the hypothesis.

10.11

> data(cervical)

> cervical$AgeNum <- rep( c(25, 35, 45, 55), 4)

> par( mfrow=c(2, 2))

> ### Part 1

> with( cervical, {

plot( Deaths/Wyears ~ AgeNum, type="n")

lines(Deaths/Wyears ~ AgeNum, lty=1,

subset=(Country==unique(Country)[1]) )

lines(Deaths/Wyears ~ AgeNum, lty=2,

subset=(Country==unique(Country)[2]) )

lines(Deaths/Wyears ~ AgeNum, lty=3,

subset=(Country==unique(Country)[3]) )

lines(Deaths/Wyears ~ AgeNum, lty=4,

subset=(Country==unique(Country)[4]) )

legend("topleft", lty=1:4, legend=unique(cervical$Country) )

})

> ### Part 3

> cc.m0 <- glm( Deaths ~ offset(log(Wyears)) + Age + Country,

data=cervical, family=poisson )

> plot( rstandard(cc.m0) ~ fitted(cc.m0), main="Poisson glm" )

> ### Part 4

> cc.m0Q <- glm( Deaths ~ offset(log(Wyears)) + Age + Country,

data=cervical, family=quasipoisson )

> plot( rstandard(cc.m0Q) ~ fitted(cc.m0Q), main="Quasi-Poisson model" )

> ### Part 5

> cc.m0NB <- glm.nb( Deaths ~ offset(log(Wyears)) + Age + Country,

data=cervical)

> cc.m0NB <- glm.convert(cc.m0NB)

> plot( rstandard(cc.m0NB) ~ fitted(cc.m0NB), main="Neg. bin. glm" )

2. To account for the exposure. 5. All models seem to have a large negative outlier, but

clearly the Poisson model does not accommodate the variation correctly.

10.13

> data(cyclones)

> par(mfrow=c(2, 2))

> scatter.smooth(cyclones$JFM, cyclones$Severe, ylim=c(0, 15))

> scatter.smooth(cyclones$AMJ, cyclones$Severe, ylim=c(0, 15))

> scatter.smooth(cyclones$JAS, cyclones$Severe, ylim=c(0, 15))

> scatter.smooth(cyclones$OND, cyclones$Severe, ylim=c(0, 15))

> par(mfrow=c(2, 2))

> scatter.smooth(cyclones$JFM, cyclones$NonSevere, ylim=c(0, 15))

> scatter.smooth(cyclones$AMJ, cyclones$NonSevere, ylim=c(0, 15))

> scatter.smooth(cyclones$JAS, cyclones$NonSevere, ylim=c(0, 15))

> scatter.smooth(cyclones$OND, cyclones$NonSevere, ylim=c(0, 15))

> ### Best models...?

> mS <- glm(Severe~1, data=cyclones, family=poisson)

> mNS <- glm(NonSevere~1, data=cyclones, family=poisson)

544 Selected Solutions

10.15

> data(polyps); library(MASS); library(statmod)

> ### Part 2

> par(mfrow=c(2, 2))

> plot( Number ~ Age, pch=ifelse(Treatment=="Drug", 1, 19), data=polyps)

> ### Part 2

> m1 <- glm(Number ~ Age * Treatment, data=polyps, family=poisson)

> plot(qresid(m1) ~ fitted(m1)); plot(cooks.distance(m1), type="h")

> qqnorm( qresid(m1)); anova(m1, test="Chisq")

> c( deviance(m1), df.residual(m1) ) # Massive overdispersion

> ### Part 3

> m2 <- glm(Number ~ Age * Treatment, data=polyps, family=quasipoisson)

> ### Part 4

> m3 <- glm.convert( glm.nb(Number ~ Age * Treatment, data=polyps) )

> anova(m2, test="F"); anova(m3, test="F")

> par(mfrow=c(1, 1))

10.19

> data(blocks)

> with(blocks,{

m0 <- glm(Number~1, family=poisson)

m1 <- glm(Number~Age, family=poisson)

coef(m1)

anova(m1, test="Chisq")

glm.scoretest(m0, blocks$Age)

})

Solutions to Problems from Chap. 11

11.3 Diﬀerentiating the log-likelihood with respect to φ gives ∂/∂φ = −n/(2φ)+

1/(2φ)



i=1

(y − ˆμ)

/(yˆμ

); solving yields the required answer.

11.5 1. As μ →∞, the expression in the exponent becomes −1/(2φy), and the result

follows. 2. var[y]=φμ

→∞as μ →∞.

> ### Part 3

> y <- seq(0.00001, 8, length=500)

> dlevy <- function(y, phi){ exp(-1/(2*y*phi))/sqrt(2*pi*phi*y^3)}

> fy1 <- dlevy(y, phi=0.5)

> fy2 <- dlevy(y, phi=1)

> fy3 <- dlevy(y, phi=2)

> plot(fy3~y, type="l", xlab="y", ylab="Density")

> lines(fy2~y, lty=2)

> lines(fy1~y, lty=3)

> legend("topright", lty=1:3, legend=c("phi = 2","phi = 1","phi = 0.5"))

> abline(h=0, col="gray")

Selected Solutions 545

11.7 Note: The main-eﬀects terms contribute 19 df also.

> ### Part 1

> DiffDf <- c(16, 12, 16, 12, 12, 16, 12, 12, 9, 12)

> ### Part 2

> phi <- 4390.9 / (1975-sum(DiffDf) - 19) # Mean deviance estimate

> ### Part 3

> Dev <- c(5050.9, 4695.2, 4675.9, 4640.1, 4598.8, 4567.3,

4497.1, 4462.0, 4443.4, 4420.8, 4390.9)

> DiffDev <- abs(diff(Dev))

> F <- (DiffDev/DiffDf)/phi

> ps <- pf(DiffDev, df1=DiffDf, df2=1975-sum(DiffDf) - 19,

lower.tail=FALSE)

>ps

11.9

> data(lime)

> ### Part 1

> lime.log <- glm( Foliage ~ Origin * log(DBH),

family=Gamma(link="log"), data=lime)

> lime.m2 <- glm( Foliage ~ Origin * DBH,

family=Gamma(link="log"), data=lime)

> par(mfrow=c(2, 3))

> ### Part 2

> scatter.smooth( log(fitted(lime.log)), rstandard(lime.log),

col="gray", lwd=2 )

> qqnorm( qresid(lime.log)); plot(cooks.distance(lime.log), type="h")

> scatter.smooth( log(fitted(lime.m2)), rstandard(lime.m2),

col="gray", lwd=2 )

> qqnorm( qresid(lime.m2));

> plot(cooks.distance(lime.m2), type="h")

> colSums(influence.measures(lime.log)$is.inf)

> colSums(influence.measures(lime.m2)$is.inf)

Prefer gamma glm with log(DBH); see the plot of standardized residuals against ﬁtted

values (on constant-information scale).

11.13

> data(fluoro)

> ### Part 1

> par(mfrow=c(2, 2))

> m1 <- glm(Dose~Time, family=Gamma(link="log"), data=fluoro)

> plot( rstandard(m1) ~ fitted(m1))

> qqnorm(rstandard(m1))

> plot( cooks.distance(m1), type="h")

> ### Part 2

> plot(Dose~Time, data=fluoro)

> newT <- seq(min(fluoro$Time), max(fluoro$Time), length=100)

> new.df <- data.frame(Time=newT)

> newD <- predict(m1, newdata=new.df, se.fit=TRUE)

> tstar <- qt(0.975, df=df.residual(m1))

> m.err <- tstar*newD$se.fit

> ci.lo <- exp(newD$fit - m.err); ci.hi <- exp(newD$fit + m.err)

> lines(exp(newD$fit)~newT, lwd=2)

> lines(ci.lo~newT, lty=2)

> lines(ci.hi~newT, lty=2)

P -values are similar.

546 Selected Solutions

11.15

> data(lungcap)

> lungcap$Smoke <- factor(lungcap$Smoke, labels=c("NonSmoker", "Smoker"))

> ### Part 1

> par(mfrow=c(3, 3))

> plot( FEV~Age, data=lungcap)

> plot(FEV~Smoke, data=lungcap)

> plot( FEV~Ht, data=lungcap)

> plot(FEV~Gender, data=lungcap)

> interaction.plot( lungcap$Smoke, lungcap$Gender, lungcap$FEV)

> interaction.plot(cut(lungcap$Age, 3), lungcap$Gender, lungcap$FEV)

> interaction.plot(cut(lungcap$Ht, 3), lungcap$Gender, lungcap$FEV)

> interaction.plot(cut(lungcap$Age, 2), lungcap$Smoke, lungcap$FEV)

> interaction.plot(cut(lungcap$Ht, 2), lungcap$Smoke, lungcap$FEV)

> ### Part 2

> m1 <- glm(FEV~Age*Ht*Gender*Smoke, family=Gamma(link="log"),

data=lungcap)

> anova(m1, test="F")

> m2 <- glm(FEV~Age*Ht*Gender+Smoke, family=Gamma(link="log"),

data=lungcap)

> anova(m2, test="F")

> par(mfrow=c(2, 4))

> plot(m1); plot(m2)

> colSums(influence.measures(m1)$is.inf)

> colSums(influence.measures(m2)$is.inf) # Prefer m2

11.17

> data(leukwbc); leukwbc$WBCx <- (leukwbc$WBC/1000)

> par( mfrow=c(1, 2))

> ### Part 1

> plot( Time ~ WBCx, data = leukwbc, las=1,

pch=ifelse(leukwbc$AG==1, 3, 1))

> legend("topright", c("AG positive","AG negative"), pch=c(3, 1) )

> ### Part 2

> plot( Time ~ log(WBCx), data = leukwbc, las=1,

pch=ifelse(leukwbc$AG==1, 3, 1))

> legend("topright", c("AG positive","AG negative"), pch=c(3, 1) )

> ### Part 3

> m1 <- glm( Time ~ AG * log10(WBCx), family=Gamma(link="log"),

data=leukwbc)

> anova(m1, test="F")

> ### Part 4

> m2 <- update(m1,.~AG+log10(WBCx))

> anova(m2, test="F")

> ### Part 5

> newW <- seq( min(leukwbc$WBCx), max(leukwbc$WBCx), length=100)

> newTP <- predict( m2, newdata=data.frame(WBCx=newW, AG=1),

type="response")

> newTN <- predict( m2, newdata=data.frame(WBCx=newW, AG=2),

type="response")

> par( mfrow=c(1, 2))

> plot( Time ~ WBCx, data = leukwbc, las=1,

pch=ifelse(leukwbc$AG==1, 3, 1))

Selected Solutions 547

> lines( newTP ~ (newW), lty=1)

> lines( newTN ~ (newW), lty=2)

> legend("topright", c("AG +ive","AG -ive"), pch=c(3, 1), lty=c(1, 2))

> plot( Time ~ log10(WBCx), data = leukwbc, las=1,

pch=ifelse(leukwbc$AG==1,3, 1))

> lines( newTP ~ log10(newW), lty=1)

> lines( newTN ~ log10(newW), lty=2)

> legend("topright", c("AG +ive","AG -ive"), pch=c(3,1), lty=c(1,2))

> ### Part 6

> summary(m2)$dispersion # Exponential seems reasonable

11.19

> data(blocks)

> ### Part 1

> ### Trial and Age (or interactions) are not significant

> glm1 <- glm(Time~Shape, data=blocks, family=Gamma(link=log))

> ### Part 2

> glm2 <- update(glm1, family=inverse.gaussian(link=log))

> ### Part 3

> plot(glm1)

> plot(glm2)

> summary(glm2)

> c(extractAIC(glm1), extractAIC(glm2))

11.22

> data(fishfood)

> m1 <- lm(FoodCon ~ log(MaxWt) + log(Temp) + log(AR) + Food,

data=fishfood)

> glm1 <- glm( FoodCon ~ log(MaxWt) + log(Temp) + log(AR) + Food,

data=fishfood, family=Gamma(link="log"))

> anova(m1)

> anova(glm1, test="F")

> summary(glm1)

> par(mfrow=c(2, 4))

> plot(m1); plot(glm1)

> c(AIC(m1), AIC(glm1))

Solutions to Problems from Chap. 12

In this chapter, we do not explicitly load the tweedie package [1] each time it is needed.

> library(tweedie)

12.1 Perform the indicated integrations.

12.7 Proceed as in Sect. 5.8 (p. 232).

548 Selected Solutions

12.11

> data(perm); perm$Day <- factor(perm$Day)

> ### Part 1

> out <- tweedie.profile( Perm ~ factor(Mach)+factor(Day),

do.plot=TRUE, data=perm)

> out$p.max; out$ci # inverse Gaussian seems appropriate

12.13

> data(motorins1); motorins1$Km <- factor(motorins1$Kilometres)

> motorins1$Bns <- factor(motorins1$Bonus)

> motorins1$Make <- factor(motorins1$Make)

> out <- tweedie.profile(Payment ~ Km * Bns, data=motorins1, do.plot=TRUE,

xi.vec=seq(1.6, 1.95, by=0.05)); xi <- out$xi.max; xi; out$ci

> ins.m1A <- glm(Payment ~ Km + Bns + Make + Km:Bns + Km:Make + Bns:Make,

data = motorins1, family=tweedie(var.power=xi, link.power=0) )

> ins.m1B <- glm(Payment ~ Km + Bns + Make + Km:Bns + Bns:Make + Km:Make,

data = motorins1, family=tweedie(var.power=xi, link.power=0) )

> ins.m1C <- glm(Payment ~ Km + Bns + Make + Km:Make + Bns:Make + Km:Bns,

data = motorins1, family=tweedie(var.power=xi, link.power=0) )

> ins.m1D <- glm(Payment ~ Km + Bns + Make + Bns:Make + Km:Bns + Km:Make,

data = motorins1, family=tweedie(var.power=xi, link.power=0) )

> anova( ins.m1A, test="F")

12.17

> data(toothbrush)

> toothbrush$Diff <- with(toothbrush, Before - After)

> with(toothbrush, interaction.plot(Sex, Toothbrush, Diff))

> out <- tweedie.profile(Diff~Sex*Toothbrush,

xi.vec=seq(1.05, 1.6, length=15),

data=toothbrush, do.plot=TRUE); xi <- round(out$xi.max, 2)

> m1 <- glm(Diff~Sex*Toothbrush, data=toothbrush,

family=tweedie(link.power=0, var.power=xi))

> anova(m1, test="F")

> summary(m1)

Solutions to Problems from Chap. 13

13.1

> data(satiswt)

> ### Part 2

> m1 <- glm( Counts~Gender+WishWt+Matur, family=poisson, data=satiswt)

> drop1( glm( Counts~Gender*WishWt*Matur, family=poisson,

data=satiswt), test="Chisq") # Need full model!

Selected Solutions 549

13.3

> data(boric)

> boric$Prob <- boric$Dead/boric$Implants

> plot( Prob~Dose, data=boric)

> m1 <- glm(Prob~Dose, weights=Implants, data=boric, family=binomial)

> m2 <- update(m1, .~log(Dose+1))

> newD <- seq(min(boric$Dose), max(boric$Dose), length=100)

> newP1 <- predict( m1, type="response", newdata=data.frame(Dose=newD))

> newP2 <- predict( m2, type="response", newdata=data.frame(Dose=newD))

> lines(newP1~newD, lwd=2, lty=1)

> lines(newP2~newD, lwd=2, lty=2)

> infl1 <- max( cooks.distance(m1))

> infl2 <- max( cooks.distance(m1))

> c(infl1, infl2)

13.5 The delivery times are strictly positive values, so a gamma or inverse Gaussian edm

may be appropriate for modelling the random component. Combining the systematic and

random components, a possible model for the data is:



y ∼ Gamma(μ; φ) (random component)

μ = β

+ β

x (systematic component).

(B.1)

> data(sdrink)

> model.sdrink <- glm( Time ~ Cases + Distance, data=sdrink,

family=Gamma(link="identity") )

> model.sdrink.iG <- glm( Time ~ Cases + Distance, data=sdrink,

family=inverse.gaussian(link="identity") )

> printCoefmat(coef(summary(model.sdrink.iG)))

> plot( rstandard(model.sdrink) ~ log( fitted(model.sdrink) ),

main="Gamma glm",

ylab="Standardized residual", las=1, pch=19 )

> plot( cooks.distance(model.sdrink), type="h",

ylab="Cook's distance", las=1)

> qqnorm( qresid(model.sdrink), las=1)

> qqline( qresid(model.sdrink))

> plot( rstandard(model.sdrink.iG) ~ log( fitted(model.sdrink.iG) ),

main="Inverse Gaussian glm",

ylab="Standardized residual", las=1, pch=19 )

> plot( cooks.distance(model.sdrink.iG), type="h",

ylab="Cook's distance", las=1)

> qqnorm( qresid(model.sdrink.iG), las=1)

> qqline( qresid(model.sdrink.iG))

While neither model looks particularly poor, the gamma glm is probably more suitable.

> c( Gamma=AIC( model.sdrink), iG=AIC(model.sdrink.iG))

> c( Gamma=BIC( model.sdrink), iG=BIC(model.sdrink.iG))

550 Selected Solutions

References

[1] Dunn, P.K.: tweedie: Tweedie exponential family models (2017). URL

https://CRAN.R-project.org/package=tweedie. R package version 2.3.0

[2] Dunn, P.K., Smyth, G.K.: GLMsData: Generalized linear model data sets

(2017). URL https://CRAN.R-project.org/package=GLMsData. R pack-

age version 1.0.0

[3] Renkl, A., Atkinson, R.K., Maier, U.H., Staley, R.: From example study

to problem solving: Smooth transitions help learning. The Journal of

Experimental Education 70(4), 293–315 (2002)

Index: Data sets

Data is not information, Information is not knowledge,

Knowledge is not understanding, Understanding is not

wisdom.

(Attributed to Cliﬀ Stoll and Gary Schubert in M. R.

Keeler. Nothing to hide: Privacy in the 21st century.

iUniverse, 2006.)

AIS, 498

ants, 417

babblers, 486

belection, 365

blocks, 28, 88, 153, 240, 262, 295, 329, 421,

452

boric, 491

breakdown, 473

bttstudy, 492

budworm, 364

butterfat, 161

cancer, 420

ceo, 160

cervical, 416

cheese, 141, 150

cins, 494

crawl, 87, 153

cyclones, 417

danishlc, 373, 416

dental, 76, 138

deposit, 354

downs, 498

dwomen, 417

dyouth,

393, 416

earinf, 495

emeraldaug, 483

energy, 482

failures, 419

ﬁneroot, 496

ﬁshfood, 150, 453

ﬂathead, 485

ﬂowers, 86, 152

ﬂuoro, 160, 449

galapagos, 499

germ, 342

germBin, 367

gestation, 32, 35

gforces, 166

gopher, 156

gpsleep, 486

grazing, 418

hcrabs, 28, 404

heatcap, 25, 128

humanfat, 27, 154

janka, 452

kstones, 386, 392

lactation, 449

leukwbc, 170, 451

lime

, 426, 429, 433, 437, 438, 448, 449

lungcap, 1, 41, 44, 97, 119, 121, 149, 150,

450

mammary, 346

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7

551

552 Index: Data sets

mandible, 29, 450

manuka, 152

motorins1, 483

mutagen, 495

nambeware, 240, 262, 295, 330, 449

nhospital, 136, 150

nitrogen, 451

nminer, 14, 168, 246, 266, 352, 366, 416

paper, 25, 156

perm, 440, 482

phosphorus, 159

pock, 398

poison, 461, 475

polyps, 418

polythene, 481

punting, 159

quilpie, 174, 463, 465, 469

ratliver, 158

rrates, 453

rtrout, 498

ruminant, 151

satiswt, 491

sdrink, 169, 493

seabirds, 329

serum, 363

setting, 156

sharpener, 90

sheep, 88, 153, 453

shuttles, 167, 363

teenconcerns, 421

toothbrush, 486

toxo, 25, 491

trees, 125, 256, 278, 305, 328

triangle, 157, 330

trout, 495

turbines, 27, 334

urinationD, 497

urinationL, 154, 453

wacancer, 395

wheatrain, 155

windmill, 121

wwomen, 421

yieldden, 442

Index: R commands

Instruction ends in the schoolroom, but education ends

only with life.

(Rev. F. W. Robertson. Sermons preached at Trinity

Chapel, Brighton. Bernhard Tauchnitz, 1866.)

Symbols

!=, 396, 510

&, 396, 510

*, 69

:, 69, 509

<, 510

<-, 508

<=, 510

==, 7, 510

>, 510

>=, 510

?, 506, 508

#, 2, 508

%*%, 45, 46, 521

^, 507

|, 510

~, 48, 516

abbreviate(), 373

abline(), 49, 50, 81, 227

add1()

for glm objects, 289, 291

for lm objects, 72, 81

AIC()

for glm

objects, 288, 289, 291

anova()

for glm objects, 270, 284, 291, 443

for lm objects, 81

arithmetic

basic, 506–508

matrix, 520–523

array(), 432

asin(), 147

attach(), 514

axis(), 373, 461

BIC()

for glm objects, 288, 291

binomial(), 257, 334

box(), 373

boxcox(), 121, 147

boxplot(), 8, 440

bs(), 132, 147

c(), 509

cbind(), 45, 360

cdplot(), 180

coef(), 49, 55

for glm objects, 250

for lm objects, 51,

colSums(), 113, 314

confint()

for glm objects, 280, 291

for lm objects, 81

contrasts, 375

contrasts(), 10

cooks.distance()

for glm objects, 313, 314, 325

for lm objects, 110, 146

cor(), 137

covratio()

for glm objects, 313, 325

for lm objects, 112, 146

cumsum(), 432

cut(), 429

data(), 2, 23, 509, 511, 512

data.frame(), 56, 267, 511

dbinom(), 175, 199

density(), 431, 432

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7

553

554 Index: R commands

det(), 522

detach(), 514

deviance(), 258, 283, 290

df.residual(), 257, 290

for glm objects, 258, 283

for lm objects, 80

dfbetas()

for glm objects, 313, 325

for lm objects, 111, 146

dffits()

for glm objects, 313, 314, 325

for lm objects, 111, 146

diag()

create diagonal matrices, 522

extract diagonal elements, 47, 188, 522

diff(), 64

digamma(), 446

dim(), 3, 521

dose.p(), 344, 356

dpois(), 227

drop(), 45, 197

drop1()

for glm objects, 289, 291

for lm objects, 72

, 81

exp(), 507, 515

extractAIC()

for glm objects, 288, 289, 291

for lm objects, 71, 81, 133, 140

F, 509

factor(), 4

FALSE, 334, 517

fitted()

for glm objects, 258, 309, 325

for lm objects, 61, 80, 146

for(), 432

function(), 227, 519

functions in r, 514–516

writing, 518–520

Gamma(), 257, 426

gaussian(), 257

gl(), 379, 411

glm(), 259, 260, 360, 443

glm.control(), 258,

259

glm.nb(), 400, 401, 411

glm.scoretest(), 271, 273, 286, 290

hatvalues(), 99, 101, 146

head, 513

head(), 2, 512

help(), 508

help.search(), 508

help.start(), 508

I(), 123, 129, 443

ifelse(), 5, 34, 392, 517

Inf, 478

influence.measures()

for glm objects, 313, 314, 325

for lm objects, 112, 113, 146

install.packages(), 505

insulate(), 147

interaction.plot(), 8

inverse.gaussian(), 257, 426

is.matrix(), 523

is.vector(), 523

jitter()

, 14, 180, 181, 398

legend(), 5, 24, 516

length(), 3, 37, 515

levels(), 373, 471

library(), 2, 505, 512

lines(), 78

list(), 519

lm(), 48, 50, 51, 79

loading data, 511–513

log(), 507, 515

log10(), 507

log2(), 507

logical comparisons, 510

margin.table(), 411

matplot(), 373, 461

matrix(), 48, 520

max(), 57

mean(), 177, 515

median(), 515

min(), 57

model.matrix(), 45, 203

names(), 23, 512

negative.binomial(), 411

nobs(), 71, 140, 288, 291

ns(), 132, 147

objects(), 514

Index: R commands 555

offset(), 289, 375

options(), 375

ordered(), 373, 375

package

GLMsData, 504, 525

MASS, 121, 344, 400, 411, 506

foreign, 512

splines, 132, 506

statmod, 257, 271, 273, 290, 301, 432,

478, 506

tweedie, 466, 475, 478, 506

help, 505

installing, 504

loading, 505

using, 505

par(), 102

paste(), 100, 519

pchisq(), 194

pexp(), 301

pi, 507

plot(), 5, 24, 147, 516

plotting,

516–518

pnorm(), 198, 286

points(), 355

poisson(), 257, 372

poly(), 129, 132, 147

power(), 258

ppois(), 302

predict()

for glm objects, 338

for lm objects, 78

print(), 276

printCoefmat(), 124, 137

prop.table(), 382, 391, 411

pt(), 279

q(), 508, 509

qnorm(), 301, 303

qqline(), 106, 146

qqnorm(), 106, 146

qqplot(), 447

qr(), 46

qresid(), 301, 325

quantile(), 132

quasi(), 257, 326

quasibinomial(), 257, 325

, 349

quasipoisson(), 257, 325, 403

quitting r, 508

range(), 79

read.csv(), 512

read.csv2(), 512

read.delim(), 512

read.delim2(), 512

read.fwf(), 512

read.table(), 512

reading data ﬁles, 511–513

relevel(), 10, 24

rep(), 175, 408

resid()

for glm objects, 299, 300, 325

for lm objects, 98, 146

residuals(), see resid()

return(), 519

rexp(), 208

rgamma(), 447

rinvgauss(), 447

rnorm(), 85, 149

round(), 314

row.names(), 276

rpois(), 328

RSiteSearch(), 508

rstandard()

for glm objects,

305, 312

for lm objects, 98, 146

rstudent()

for glm objects, 312

for lm objects, 109, 146

runif(), 302

sapply(), 227

scatter.smooth(), 101, 102

sd(), 515

seq(), 227, 509

sin(), 507

solve(), 45, 46, 188, 522

sort, 99

sqrt(), 38

step()

for glm objects, 289–291

for lm objects, 72, 81

str(), 2, 32, 342, 512

subset(), 6, 80, 315, 396, 450

sum(), 37, 463, 515

summary(), 4

, 32

for glm objects, 258, 260, 290, 444

for lm objects, 51, 59, 80

for data frames, 513

T, 509

t(), 45, 509, 521

tail(), 2, 512

556 Index: R commands

tapply(), 218, 441, 461, 462, 471

termplot(), 103

terms(), 80

text(), 100, 471

trigamma(), 446

TRUE, 334

tweedie(), 257, 469, 478, 479

tweedie.convert(), 472

tweedie.profile(), 466, 475, 478

update()

for glm objects, 259, 283

for lm objects, 61, 63, 80

var(), 98, 515

weighted.mean(), 37

which.max(), 314

wilcox.test(), 273

with(), 203, 405, 514

writing functions, see functions in r

xtabs(), 373, 379, 394, 396

zapsmall(), 129

Index: General topics

Knowledge is of two kinds. We know a subject ourselves,

or we know where we can ﬁnd information upon it.

(Attributed to Samuel Johnson in J. Boswell and R. W.

Chapman. Life of Johnson. Oxford World’s Classics.

Oxford University press, third edition, 1988.)

accuracy, 20

adjusted R

, see

aic

deﬁnition, 202

for glms, 288–289

for linear regression, 70–72

Akaike’s Information Criterion, see aic

analysis of deviance, 270–271, 284–286

analysis of deviance table, 270, 285, 294

analysis of variance, 59–70

analysis of variance table, 69–70

ANOVA, see analysis of variance

Anscombe residuals, see residuals

asymptotic theory

large sample, 273–274

small dispersion, 276–278

automatic variable selection

backward elimination, 74, 289

for glms, 289–290

for linear regression, 73–75

forward regression, 74, 289

objections, 76

stepwise, 74, 289

Bayesian Information Criterion, see bic

Bernoulli distribution, 175, 367

beta distribution, 235, 348

bic

deﬁnition, 71, 202

for glms, 288–289

for linear regression, 70–72

binomial distribution, 212, 252

equivalent transformation in linear

regression, 233

probability function, 213

table of information, 221

Brownian motion, 440

candidate variables, see variables,

explanatory

canonical parameter, 212, 221

carriers, see variables, explanatory

categorical variable, see variables,

categorical

Cauchy distribution, 236

Central Limit Theorem, 225, 226, 276, 277

accuracy, 225, 277

chi-square distribution, 408, 430

coding qualitative variables, 11, 375

polynomial, 375

treatment coding, 11, 375

coeﬃcient of variation, 428

collinearity, 135–138, 321–322

conﬁdence intervals for

for glms, 266–267

for linear regression, 55–56

conﬁdence intervals for ˆμ

for glms, 267–268

for linear regression, 56–57

constant-information scale, 307

contrasts, 10,

374

Conway–Maxwell–Poisson distribution,

237

Cook’s distance, 110

for glms, 313

interpretation, 313

for linear regression, 110, 149

interpretation, 110, 149

high values, 112

P. K. Dunn, G. K. Smyth, Generalized Linear Models with Examples in R,

Springer Texts in Statistics, https://doi.org/10.1007/978-1-4419-0118-7

557

558 Index: General topics

count responses, 166, 168, 371–412

covariance ratio

for glms, 313

for linear regression, 111, 112

high values, 112

covariates, see variables, explanatory

cran, 504

cumulant function, 212, 215, 221

cumulant generating function, 214

cumulants, 214

cumulative distribution function, 302,

319, 336, 339

cumulative probability function, 301

cv, see covariance ratio

degrees of freedom (residual), see residual

degrees of freedom

dependent variables, see variables,

response

designed experiment, 22

deviance, 231, 276

residual deviance, see residual deviance

scaled, 231, 248

total, 231, 248

deviance function, 231

deviance residuals, see residuals

dfbetas

for glms, 313

for linear regression, 111

high values, 112

dffits

for glms, 313

for linear regression, 111

high values, 112

dispersion model form, 220

dispersion parameter φ, 212, 216, 221

estimation, 252–256, 436–439

gamma distribution, 436

inverse Gaussian distribution, 439

Tweedie distribution, 464, 471

maximum likelihood estimator, 253, 471

mean deviance estimator, 254

modiﬁed proﬁle log-likelihood

estimator, 253

Pearson estimator, 255

preferred estimator, 255

distribution, see exponential dispersion

models; the speciﬁc distributions

dose–response models, 343

downscaling, 472

dummy variable, see variable

ecological fallacy, 79

ed50, 343–344, 361

edms, see exponential dispersion models

Erlang distribution, 431

expected information, see information

explanatory variables, see variables,

explanatory

exponential dispersion models (edms),

212–218, see distribution

cgf, 215

mgf, 215

canonical form, 212

deﬁnition, 212

dispersion model form, 218–224

examples, 212, 221

log-likelihood, 244

mean,

216

table of information, 221

variance, 216

exponential distribution, 239, 301, 430

exposure, 230

extended quasi-likelihood, 321

extraneous variable, see variables,

extraneous

factors, 11, 23

coding, 10, 11

treatment coding, 10–11

Fisher information, see information

Fisher scoring, 186, 245, 250

ﬁtted values

for linear regression, 37

gamma distribution, 212

equivalent transformation in linear

regression, 233

probability function, 217, 236, 427

special cases, 430

table of information, 221

gamma function, 428, 445

generalized hyperbolic secant distribution,

238

generalized linear model, 13, 335

assumptions, 297–298

binomial, 231, 333–361

deﬁnition, 230–231

gamma, 425–446

inverse Gaussian, 425–446

notation, 231

Poisson, 15, 371–412

Index: General topics 559

Tweedie, 457–479

two components, 211

generating functions

cumulant, 214

moment, 214

geometric distribution, 235

goodness-of-ﬁt tests, 274–276, 347, 354

deviance, 275

guidelines for use, 276

Pearson, 275

hat diagonals, see leverage

hat matrix, 100, 304

hat values, see leverage

Hauck–Donner eﬀect, 200, 352, 353

hypothesis testing, 191–200

for glms

methods compared, 287–288

with φ known, 265–273

with φ unknown, 278–287

for linear regression, 54–55

global tests, 194

likelihood ratio test, 192

methods compared, 199

one parameter in a set, 197

score test, 191

subsets of parameters, 196

Wald test, 191

independent variables, see variables,

explanatory

inﬂuential observations

deﬁnition, 110

for glms, 313–315

for linear regression,

110–115

information

expected (Fisher), 178, 184, 245, 250

observed, 178, 185

interaction, 67, 74

interaction plot, 8

interpretation, 18

inverse Gaussian distribution

equivalent transformation in linear

regression, 233

probability function, 237, 431

table of information, 221

irls, see iteratively reweighted least

squares

iteratively reweighted least squares, 246,

251

knots, 132

large sample asymptotics, see asymptotic

theory

lc50, 343

ld50, 343

levels of a factor, 3

leverage

for glms, 313

for linear regression, 97, 99, 149

high values, 112

likelihood function, 173, 183

likelihood ratio test, 269, see hypothesis

testing

limiting dilution assay, 344

linear predictor, 12, 212, 229

linear regression model, 12, 31

assumptions, 94–97

normal linear regression model, 53

link function,

180, 229

canonical, 221, 229, 239

complementary log-log, 336, 361

inverse (reciprocal), 436

logarithmic, 361, 430, 433, 436, 464

logistic, see link function, logit

logit, 336, 361

power, 258

probit, 336, 339, 361

log-likelihood

modiﬁed proﬁle, 253

proﬁle, 253, 466

log-likelihood function, 173, 183

log-linear model, 372, 378–397

logarithmic link, see link function

logistic distribution, 361

logistic link, see link function

logistic regression model, 336, 362

logit link, see link function

longitudinal study, 19

Lévy distribution, 447

marginality principle, 70, 387

maximum likelihood estimates

properties, 189

maximum likelihood estimation, 172–191

maximum likelihood estimator, 173

model

purpose, 71

role, 11

model formula, 48

model matrix, 43, 84

, 272

models, 11–12

causality, 21–22

compare physical and statistical, 17

560 Index: General topics

models (cont.)

criteria, 19–20

experiments, 21–22

generalizability, 22–23

interpretation, 16–17

limitations, 21–23

nested, 61, 69, 70, 288

observational studies, 21–22

purpose, 18

modiﬁed saddlepoint approximation, see

saddlepoint approximation

moment generating function, 214, 238, 239

multicollinearity, see collinearity

multinomial distribution, 383

multiple R

, see R

negative binomial distribution, 212,

399–401

probability function, 400

table of information, 221

nested models, see models

Newton–Raphson method, 186

noise, see random component

normal distribution, 174, 212, 216

probability function, 174, 213

table of information, 221

nuisance parameter, 196

observational studies, 21

observed information, see information

Occam’s Razor, 20

odds, 340

odds ratio, 341

oﬀset, 229–230, 289, 375

orthogonal polynomials, see polynomials

outliers, 108–124, 312–313, see residuals

inconsistent, 109

inﬂuential, 112, 313

remedies, 134–135

over-ﬁtting, 20

overdispersion, 320, 347, 397

binomial glms, 347–351

Poisson glms, 397–399

parsimony, 20

partial residual plot

for glms, 308

for linear regression, 102

partial residuals

for glms, 308

for linear regression, 102

Pearson residuals, see residuals

Pearson statistic, 255, 271, 276, 277, 299

Poisson distribution, 212, 216, 252

equivalent transformation in linear

regression, 233

probability function, 213, 371

residual deviance, 249

table of information, 221

Poisson regression model, 372

polynomial regression, 127–131

polynomials, 316

orthogonal, 129

raw, 129

positive continuous responses, 166,

425–446

positive continuous responses with zeros,

457–479

prediction, 18

predictors, 3

principle of parsimony, 20

prior weights, 31, 230, 235, 396

probability density function, 173, 212

probability function, 173, 212

probability mass function, 212

proﬁle likelihood, see likelihood, proﬁle

proﬁle likelihood plot, 478

proportion responses, 166, 333–361

Q–Q plots, 105–106, 109, 312, 408, 469,

474

QR-decomposition, 45, 46

qualitative variable, see variable,

qualitative, see variable

quantile residuals, see residuals, quantile,

see residuals

quantitative variable, see variable,

quantitative, see variable

quasi-binomial, 325, 348–351

quasi-likelihood, 319

quasi-Poisson, 402–404

r Commander, 503

r homepage, 504

r libraries, 504–506

r package

foreign, 512

GLMsData, 504, 525

MASS, 121, 344, 400, 411, 506

splines, 132, 506

statmod, 257, 271, 273, 290, 301, 432,

478,

506

tweedie, 466, 475, 478, 506

Index: General topics 561

(multiple R

), 59

(adjusted R

), 60

random component, 11, 31, 211

random zeros, see zero counts

randomized quantile residuals, see

residuals, quantile

raw polynomials, see polynomials

regression

all possible models, 74

automatic variable selection, 72–75, 289

independent, 66–70

parallel, 66–70

weighted, 32–35

regression model, see linear regression

model; generalized linear model

deﬁnition, 12–16

examples, 165–171

interpretation, 52–53

linear, see linear regression model

linear in the parameters, 12

multiple, 32

normal linear, see linear regression

model

ordinary linear, 32

simple linear, 32

weighted linear, 32

regression parameters, 11

regression splines, 131–133, 316, 325

regressors, see variables, explanatory

residual degrees of freedom, 284

residual deviance, 248–249, 269, 270, 275,

277, 284,

305

residual sum-of-squares, 37, 42, 59, 71, 97

residuals, see outliers

Anscombe, 328

deviance, 300, 306

Pearson, 299–300, 327, 328

quantile, 300–304

raw

for glms, 305

for linear regression, 37, 38, 97

response, 298

standardized, 97

for glms, 305–306

for linear regression, 115

Studentized, 115

for glm, 312

for linear regression, 109

working, 252, 304

response variable, see variables, response

rss, see residual sum-of-squares

RStudio, 503

saddlepoint approximation, 223–226, 276

accuracy, 225, 277

modiﬁed, 223

sampling zeros, see zero counts

saturated model, 274, 275, 389

scaled deviance, see deviance, scaled,

see

deviance

Schwarz’s Bayesian criterion, see bic

score equation, 176, 182, 184, 245

score function, 176, 182, 183

score test, see hypothesis testing

score vector, 183

signal, see systematic component

Simpson’s paradox, 389–391, 421

single-hit model, 345

small dispersion asymptotics, see

asymptotic theory

S-Plus, 504

standard errors, 39, 47, 104, 190, 191,

250–251, 265, 273

inﬂated, 352, 403

standardized quantile residuals, see

residuals

standardizing, 115

strict arcsine distribution, 236

structural zeros, see zero counts

Studentized residuals, see residuals

Studentizing, 115

sum-of-squares (residual), see residual

sum-of-squares

systematic component, 11, 32, 212

tolerance distribution, 339

transformations

arcsin, 119, 361

Box–Cox, 120–121

logarithmic,

119

of covariates, 121–124

of covariates and response, 125

of the response, 116–121

variance-stabilizing, 118

treatment coding, see coding

Tweedie distribution, 239

equivalent transformation in linear

regression, 233

probability function, 460

rescaling identity, 461

special cases, 457

table of information, 221, 458

Tweedie index parameter, 458, 459

562 Index: General topics

underdispersion, 347, 397

unit deviance, 218–223

approximate χ

distribution, 224, 226

variables

covariates, 3

dummy, 10, 11

explanatory, 3

extraneous, 3

factors, 3, see factors

response, 3

variance function, 216, 217, 221, 239

variation, see random component

von Mises distribution, 172, 236

Wald statistic, 197

Wald test, see hypothesis testing

Weibull distribution, 213

Wood’s lactation curve, 449

working residual, see residuals

working responses, 246, 308

working values, 246

working weights, 245

zero counts

sampling, 395

structural, 395

zero-truncated Poisson distribution, 413